玻璃纤维增强复合材料筋与超高性能混凝土之间粘结-滑移本构模型

薛文远,胡翔,薛伟辰

(1.斯坦福大学 土林与环境工程系,加利福尼亚 94305;2.同济大学 建筑工程系,上海 200092)

钢筋混凝土结构具有受力性能良好、可模性好和造价低廉等优点,但其中的钢筋锈蚀问题突出,这将造成严重的安全隐患和巨大的经济损失[1]。此外,混凝土材料本身也存在着强度较低、脆性较大和粘结性能较差等问题[2]。为解决上述问题,近年来国内外学者开始尝试采用超高性能混凝土(ultra-high-performance concrete,UHPC)和纤维增强复合材料筋(fiber reinforced polymer rebar,FRP筋)代替传统钢筋混凝土结构中的混凝土和钢筋。

UHPC是一种新型超高性能水泥基复合材料,其主要组分通常包括水泥、细沙、石英砂粉和高效减水剂等。UHPC具有超高强度、高韧性和高耐久性等优点[2]。通过优化颗粒级配以及掺入活性矿物掺合料和钢纤维等措施[2],UHPC的抗压强度可达150 MPa以上,抗拉强度可达8 MPa以上。在实际工程中,采用UHPC替代普通混凝土可大幅度减小截面尺寸、减轻结构自重并提高结构耐久性。此外,相比普通混凝土,UHPC与钢筋的粘结性能优良[3-4]。

FRP筋是一种由连续纤维与树脂加工成型的棒材,根据纤维种类的不同,可分为玻璃纤维增强复合材料筋(GFRP筋)、碳纤维增强复合材料筋(CFRP筋)、芳纶纤维增强复合材料筋(AFRP筋)和玄武岩纤维增强复合材料筋(BFRP筋)等几种。相比钢筋,FRP筋具有重量轻、强度高和耐久性好等优点,但也存在着粘结性能相对较差等不足。为提高FRP筋与普通混凝土之间的粘结性能,通常对FRP筋表面进行处理,如用纤维束在其表面缠绕形成一定高度的“肋”(以下简称“绕肋”)、通过切割形成螺纹形的凹槽(以下简称“螺纹”)或粘附砂粒(以下简称“粘砂”)[5]等。

为解决传统钢筋混凝土结构中的钢筋锈蚀问题,进一步提高结构的力学性能和耐久性,FRP筋UHPC结构已成为近年来国内外土木工程研究领域的新热点,尤其在海洋工程等腐蚀性环境下具有重要工程应用价值,而FRP筋与UHPC之间良好的粘结性能则是保证两者共同工作的基础。

关于FRP筋与普通混凝土之间的粘结性能,国内外已开展了较为系统的试验和理论研究,多个国家的规范(日本JSCE 1997[6]、美国ACI 440.1R-15[7]、加拿大CAN/CSA S806—02[8]、中国GB 50608—2010[9]和CJJ/T 280—2018[10]等)中均已提出了FRP筋在普通混凝土中的锚固长度设计规定,相应的粘结-滑移本构模型(Malvar模型[11]、CMR模型[12]和mBPE模型[13]等)也比较成熟。自1995年以来,文献[14-18]通过一系列试验对CFRP筋、GFRP筋、AFRP筋和CFRP索在普通混凝土中的粘结性能进行了深入的研究,提出了粘结强度、锚固长度及粘结-滑移本构模型的计算公式,部分成果已纳入国家行业标准CJJ/T 280—2018[10]中。

关于钢筋与UHPC之间的粘结性能,国内外的研究也比较成熟,日本JSCE 2008[19]、法国NF P 18—710[20]、瑞士MCS-EPFL[21]和《湖南省活性粉末混凝土结构技术规程》[22]中均包含了UHPC中钢筋锚固长度的设计规定。

关于FRP筋与UHPC之间的粘结性能,国外已开展了一系列试验研究,而相关的理论研究尚不完善。国内在该方面的研究几乎为空白。鉴于此,本文针对工程中常见的GFRP筋开展研究,总结已有GFRP筋与UHPC之间粘结性能的试验研究成果,分析得到了粘结强度的主要影响因素及其影响规律,在此基础上提出了粘结强度和锚固长度的计算公式,并进一步提出了粘结-滑移本构模型的计算公式。

1 已有研究概述

1.1 已有试验研究成果

Ametrano[23]和Hossain等[24-25]最早开展了GFRP筋与UHPC之间的粘结性能研究,通过84个拉拔试件和42个梁式试件研究了UHPC抗压强度、GFRP筋弹性模量、FRP筋直径、粘结长度和保护层厚度等因素对粘结强度的影响。瑞尔森大学的Sayed-Ahmed等[26-27]开展了110个拉拔试件的试验研究,研究参数包括UHPC抗压强度、粘结长度和保护层厚度等。Michaud等[28]通过14个梁式试件研究了保护层厚度较小时钢纤维掺量和粘结长度对粘结性能的影响。Yoo等[29-30]通过25个拉拔试件研究了FRP筋直径和粘结长度对粘结强度和粘结-滑移曲线的影响。

1.2 破坏模式和粘结-滑移曲线

已有研究表明,与普通混凝土中的FRP筋类似[31],GFRP筋与UHPC之间的粘结破坏模式以拔出破坏为主[23-27,29-30,32],当保护层厚度小于2倍FRP筋直径时,试件可能发生劈裂破坏[28]。粘砂GFRP筋和绕肋GFRP筋发生拔出破坏时通常伴随着表层部分剥离[24-25,30],螺纹GFRP筋发生拔出破坏时通常伴随着肋被剪断[27]。

UHPC中GFRP筋的粘结-滑移曲线如图1所示,其中粘砂GFRP筋和绕肋GFRP筋的曲线分别来自文献[23,30]。粘砂GFRP筋产生微小滑移时即发生拔出破坏,峰值粘结力对应的滑移量sm约为0.05～0.2 mm[23]。绕肋GFRP筋第1次达到峰值粘结力时的滑移量为0.92～1.76 mm[30],随后由于楔块效应(随滑移增加,GFRP筋无粘结区段进入粘结区段)粘结力下降一定幅度并再次上升,最终发生拔出破坏或劈裂破坏。由于此时GFRP筋自由端滑移量已达到2～4 mm以上,在实际工程中意义不大,故可将粘结力的第1个峰值点作为极限状态,并认为试件发生拔出破坏[30]。

图1 UHPC中GFRP筋的粘结-滑移曲线[23,30]Fig.1 Bond-slip curves of GFRP rebar in UHPC

综上可见,针对GFRP筋与UHPC之间的粘结性能,国外学者已开展了大量的试验研究,并为本文后续工作奠定了基础。

2 粘结强度的主要影响因素

已有试验表明[23-30,32],GFRP筋与UHPC之间粘结强度的主要影响因素包括FRP筋直径db、粘结长度Le、保护层厚度c、UHPC圆柱体抗压强度fc′和试验方法。需要说明,相比Le和c,相对粘结长度Le/db和相对保护层厚度c/db能更直观地反映粘结强度的变化规律,已有的GFRP筋-UHPC粘结性能试验研究中通常将Le/db和c/db作为试验参数[23-30,32],美国ACI 440.1 R-15[11]也将粘结强度表示为关于Le/db和c/db的函数,故本文采用同样的方式开展分析。

2.1 FRP筋直径db

关于FRP筋直径对粘结强度的影响,目前国际上的试验结果尚无一致性的规律。加拿大瑞尔森大学的Ametrano[23]和Hossain等[24-25]的试验表明,梁式试件中粘结强度随FRP筋直径的增加而降低,相比直径15.9 mm的GFRP筋,直径19.1 mm的GFRP筋的粘结强度平均降低了12%,而拉拔试验中不同直径的GFRP筋的粘结强度差异很小。Yoo等[30]的试验表明,随FRP筋直径增加,粘结强度提高,相比直径为12.7 mm的GFRP筋,直径15.9 mm的GFRP筋的粘结强度平均提高了22%。

已有文献分析了上述现象的机理：在普通混凝土中,FRP筋周围的混凝土的泌水效应影响了二者间的接触,因此粘结强度随FRP筋直径增加而降低[23-24]。在UHPC中该现象并不明显,其原因包括2个方面：1)UHPC水灰比较低,泌水效应较弱[23];2)UHPC中掺入的钢纤维影响了FRP筋与UHPC之间的接触面,进而降低了粘结强度,钢纤维长度不变时,直径越小的FRP筋受到的扰动越大[23]。

综上可见,基于已有试验结果,FRP筋直径对粘结强度的影响尚无一致性的规律,故本文后续理论分析中不直接将FRP筋直径作为粘结强度的主要影响参数。

2.2 GFRP筋相对粘结长度Le/db

大量试验表明[23-25,28,30,32],随GFRP筋的相对粘结长度增加,GFRP筋与UHPC之间的粘结强度有所降低。当相对粘结长度Le/db从3增加至5和7时,粘结强度平均下降了18%和22%[23-24]。

粘结强度降低的原因包括[23,25,30,32]：1)随粘结长度增加,粘结应力分布的不均匀程度增大;2)随粘结长度增加,峰值荷载提高,FRP筋加载端拉应变增大,同时因泊松效应导致的FRP筋径向收缩增大,减小了UHPC自收缩在FRP筋周围引起的约束力。

2.3 GFRP筋相对保护层厚度c/db

随相对保护层厚度c/db增加,GFRP筋在UHPC中的粘结强度提高。加拿大瑞尔森大学的Sayed-Ahmed[26]的试验表明,对于相对粘结长度Le/db=6,8的拉拔试件,相比中心锚固(c/db=4.5),偏心锚固(c/db=2)时FRP筋的粘结强度分别降低了12%和6.5%。可见：随相对保护层厚度增加,UHPC对GFRP筋的约束增强[23],因而粘结强度提高。

2.4 UHPC抗压强度fc′

试验表明,随UHPC抗压强度提高,UHPC与GFRP筋之间的粘结强度提高[23-25]。当fc′从148 MPa提高到175 MPa时,粘结强度平均提高了13%[23-25]。

粘结强度提高的原因包括[23-24]：1)水灰比越低,UHPC抗压强度越高,同时UHPC自收缩效应越强,从而在FRP筋周围形成了更大的静水压力,提高了粘结强度;2)UHPC中掺入的钢纤维提供了额外约束。

2.5 试验方法

已有试验表明,对于梁式试件和拉拔试件,粘结强度均随UHPC抗压强度提高而提高,随相对粘结长度增加而降低[23-25]。以粘砂GFRP筋为例,梁式试件和拉拔试件的粘结强度平均值分别为16.3 MPa和20 MPa[23,25-26]。第3节中将基于统计分析进一步研究不同试验方法对粘结强度的影响。

2.6 FRP筋表面形态

相关研究表明[33],FRP筋的表面形态对其与普通混凝土之间的粘结性能有重要影响,而FRP筋与UHPC之间也存在同样的现象。试验表明[23,25-27,29-30],绕肋GFRP筋、粘砂GFRP筋和螺纹GFRP筋在UHPC中的粘结强度分别为16.3～28.6 MPa、10.4～29.8 MPa和9.0～19.9 MPa。由于螺纹GFRP筋的“肋”的表面相比粘砂GFRP筋和绕肋GFRP筋的表面更为光滑(如图2),故其粘结强度较低。

图2 典型的GFRP筋表面形态Fig.2 Typical surface types of GFRP rebar

综上,粘结强度随UHPC抗压强度和相对保护层厚度的提高而提高,随相对粘结长度增加而降低;FRP筋直径对粘结强度的影响尚无一致性的规律;梁式试件的粘结强度略高于拉拔试件;螺纹GFRP筋的粘结强度低于绕肋GFRP筋和粘砂GFRP筋。第3节中将基于上述影响规律进一步开展分析。

3 粘结强度与锚固长度

定义FRP筋的粘结强度为发生粘结破坏时粘结区段的平均粘结应力：

(1)

式中：db和Le分别为FRP筋的直径和粘结长度;τu为FRP筋的粘结强度;F为发生粘结破坏时FRP筋所受拉力。

3.1 国内外规范中有关普通混凝土中FRP筋粘结强度及锚固长度的设计规定

目前,日本、加拿大、美国和中国等均制订了FRP筋混凝土结构的设计规范,各规范均纳入了有关普通混凝土中FRP筋锚固长度的设计规定。而针对UHPC中FRP筋的锚固长度,现行规范尚无相关规定。

1) 日本规范：Recommendation for design and construction of concrete structures using continuous fiber reinforcing materials JSCE 1997[6]。

(2)

(3)

式中：fbod为粘结强度;α2为考虑FRP筋特性的系数,可由试验确定;fck′为混凝土抗压强度;γc为粘结强度折减系数;ld为锚固长度;α1为考虑保护层厚度与箍筋的系数;fd为FRP筋抗拉强度;db为FRP筋直径。

2) 美国规范：Guide for the design and construction of concrete reinforced with FRP bars ACI 440.1R-15[7]。

(4)

leπdbu=Afff

(5)

式中：u为粘结强度;fc′为混凝土抗压强度;c为FRP筋形心到混凝土外表面距离与1/2倍FRP筋形心距离中的最小值;db为FRP筋直径;le为锚固长度;Af为FRP筋截面积;ff为FRP筋粘结区段端部的应力。

3)加拿大规范：Design and construction of building structures with fibre reinforced polymers CAN/CSA S806-02[8]。

(6)

式中：ld为锚固长度;k1、k2、k3、k4和k5分别为考虑FRP筋位置、混凝土密度、FRP筋面积、FRP筋纤维类型和FRP筋表面形态影响的系数,其中对粘砂GFRP筋和绕肋GFRP筋k5取1.0,对螺纹GFRP筋k5取1.8;dcs为FRP筋形心到混凝土外表面距离与2/3倍FRP筋形心距离中的最小值;ff为FRP筋抗拉强度;fc′为混凝土抗压强度;Ab为FRP筋截面积。

4) 加拿大规范：Canadian highway bridge design code CAN/CSA-S6—14[34]。

(7)

式中：ld为锚固长度;k1、k4和ktr分别为考虑FRP筋位置、FRP筋表面形态和横向箍筋影响的系数;dcs定义同式(6);EFRP为FRP筋弹性模量;Es为钢筋弹性模量;fcr为混凝土开裂强度;fFRPu为FRP筋抗拉强度;A为FRP筋截面积。

5) 中国规范：纤维增强复合材料筋混凝土桥梁技术标准：CJJ/T 280—2018[10]。

(8)

式中：la为锚固长度;ffd为FRP筋抗拉强度;ftd为混凝土抗拉强度。

对比上述规范中的锚固长度计算公式,其主要影响参数有所差异,如表1。得出如下结论。

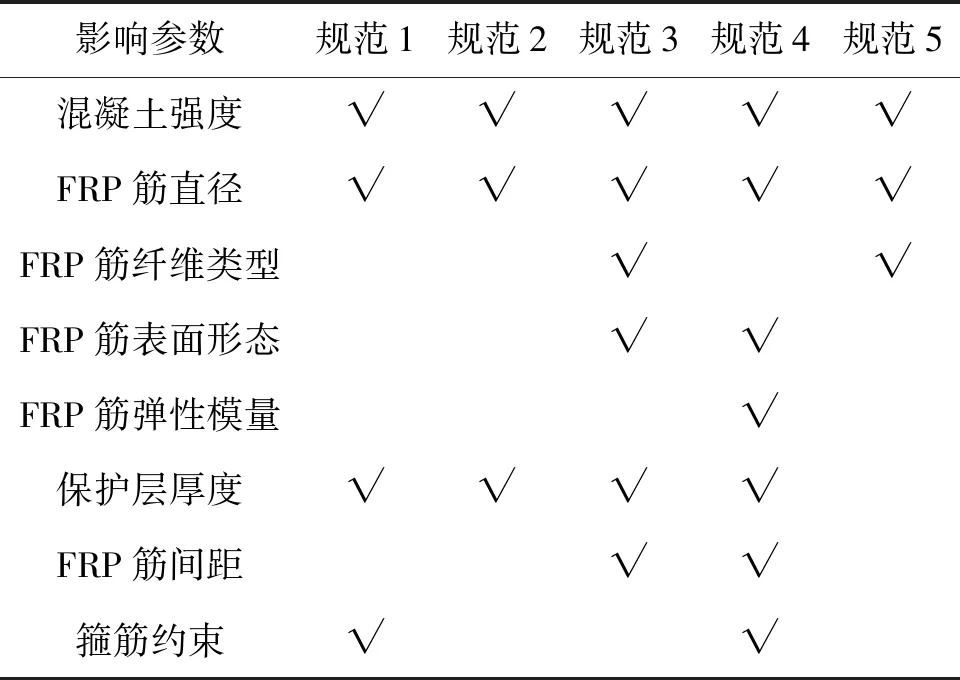
表1 已有规范中FRP筋与普通混凝土之间锚固长度的主要影响参数Table 1 Major influence factors of development length between FRP rebar and concrete in available design codes

1)上述5个规范均考虑了混凝土强度提高对粘结性能的有利影响。

2)CAN/CSA S806—02和CAN/CSA S6—14考虑了FRP筋表面形态的影响。CAN/CSA S806—02认为螺纹GFRP筋的锚固长度大于粘砂GFRP筋和绕肋GFRP筋,这与第2节中的结论一致。

3)上述规范中仅CJJ/T 280—2018忽略了保护层厚度的影响。

4)JSCE 1997和ACI 440.1R—15给出了粘结强度计算公式,其中ACI 440.1R—15的计算公式考虑了相对粘结长度Le/db和相对保护层厚度c/db,而这二者也均为UHPC中GFRP筋粘结强度的主要影响因素(详见第2节),故本文研究粘结强度计算公式时借鉴式(4)开展分析。

3.2 已有UHPC中GFRP筋粘结强度与锚固长度的理论研究成果

目前,仅有个别学者开展了针对UHPC中GFRP筋粘结强度与锚固长度的理论研究。加拿大瑞尔森大学的Ametrano[23]对FRP筋普通混凝土结构规范(JSCE 1997、ACI 440.1R—06、CAN/CSA S806—02和CAN/CSA S6—06)进行了验算,结果表明上述规范中对锚固长度的规定均偏于保守。瑞尔森大学的Sayed-Ahmad[27]建议螺纹GFRP筋在UHPC中的锚固长度不小于9.5db和152 mm。Michaud等[28]的研究表明ACI 440.1R—06和CAN/CSA S806—02对锚固长度的规定偏于保守,同时提出了粘砂GFRP筋粘结强度的计算公式：

(9)

并建议对钢纤维掺量为2%和4%的UHPC,GFRP筋的锚固长度分别取29db和20db。Yoo等[30]基于ACI 440.1 R—15规范,通过68个拉拔试验结果的回归分析提出了GFRP筋与UHPC之间粘结强度和锚固长度的计算公式：

(10)

(11)

需要说明,在上述粘结长度计算公式中,式(9)仅基于发生劈裂破坏的试件得到,且未考虑相对粘结长度的影响;式(9)和(10)均未考虑相对保护层厚度和FRP筋表面形态的影响,且验证的试验数据偏少。此外,系统收集的195个粘结试验结果表明UHPC中GFRP筋粘结强度的变异性较大,而尚未有学者提出考虑保证率的粘结强度和锚固长度计算公式。

3.3 本文提出的GFRP筋与UHPC之间粘结强度计算公式

已有文献报道中绝大多数UHPC-GFRP筋粘结试件均发生拔出破坏,发生劈裂破坏的试件数量非常少,故本文暂不考虑劈裂破坏模式。此外,有学者分析,对于发生劈裂破坏的试件,当粘结长度不变时,随保护层厚度c不断增加,其破坏模式将逐渐过渡到拔出破坏[33]。基于试验结果,为避免发生劈裂破坏,要求c≥2db。而当c<2db时,试件可能发生劈裂破坏,相应的粘结强度和锚固长度有待进一步研究。

基于已有试验中发生拔出破坏的153个GFRP筋拉拔试件和42个GFRP筋梁式试件,按FRP筋表面形态和试验方法分为4组,分别为G-HW组(绕肋GFRP筋-拉拔试验)、G-I组(螺纹GFRP筋-拉拔试验)、G-SC组(粘砂GFRP筋-拉拔试验)和G-SC-B组(粘砂GFRP筋-梁式试验),如表2。GFRP筋表面形态如图2所示。

表2 已有试验中的GFRP筋粘结试件汇总Table 2 Summary of GFRP rebar bonding specimens in available tests

基于上文对粘结强度主要影响因素的分析,考虑FRP筋表面形态和试验方法的影响,借鉴ACI 440.1R—15提出的式(4),提出了UHPC中GFRP筋粘结强度计算公式的基本形式：

(12)

式中：k1、k2和k3为回归得到的系数,其中k1和k2与FRP筋表面形态和试验方法有关,k3取0.01;db为FRP筋直径;Le为粘结长度;c为保护层厚度,当c/db>3.5时,取c/db=3.5;τu为粘结强度,MPa;fc′为UHPC圆柱体抗压强度或立方体抗压强度,MPa。

表3 粘结强度计算公式中系数k1和k2的取值Table 3 Values of k1 and k2 for calculation method of bond strength

表4 粘结强度计算值与试验值的均值与变异系数对比Table 4 Comparison of theoretical and experimental values of bond strength

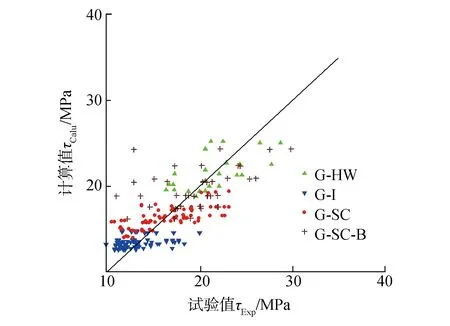
图3 本文提出的粘结强度计算值与试验值的对比Fig.1 Comparison of theoretical bond strength provided by this study with experimental bond strength

1)JSCE 1997提出的式(2)的计算值明显偏大,这是由于该公式高估了UHPC抗压强度的提升对粘结强度的有利影响所致。此外,该公式未考虑相对粘结长度等因素的影响。

2) 梁式试件测得的粘结强度略高于拉拔试件测得的粘结强度。粘结长度越小,前者高出的幅度越大。

3) 无论对哪种表面形态的GFRP筋,ACI 440.1R—15提出的式(4)的计算值均偏小。

4) Yoo提出的式(10)适用于绕肋GFRP筋。由于该公式未考虑FRP筋表面形态和试验方法的影响,其高估了螺纹GFRP筋的粘结强度,低估了粘砂GFRP筋梁式试件的粘结强度。

5) Michaud提出的式(9)与试验结果相比误差较大。由于忽略了相对粘结长度和表面形态等因素的影响,该公式不适用于发生拔出破坏的试件。

6)本文提出的式(12)综合考虑了FRP筋表面形态和相对粘结长度等因素的影响,得到的计算值与试验结果吻合良好。

3.4 基于区间预测的UHPC中GFRP筋粘结强度与锚固长度计算公式

锚固长度Le即粘结破坏与FRP筋拉断破坏同时发生时的粘结长度,满足：

(13)

式中ff为FRP筋抗拉强度。

(14)

式中：n为该组试件的数量;tn-2(α)为自由度为n-2的t分布的1-α分位数;tn-2(α)Δ项为置信水平为1-α的置信下界与预测值均值之差,反映了为使粘结强度达到1-α保证率对其作出的折减,其中Δ按式(15)计算。

(15)

(16)

(17)

(18)

(19)

式中K为系数,与GFRP筋表面形态等因素有关。

借鉴国家标准GB50608—2010[9]中对FRP筋抗拉强度保证率的要求,取α=0.05,即保证率为95%。取c=2db,对于工程中常见的GFRP筋(ff≤1 500 MPa)和UHPC(fc′≥120 MPa),可得：对绕肋GFRP筋,K=6.3;对螺纹GFRP筋,K=4.5;对粘砂GFRP筋,K=6.0。

4 粘结-滑移本构模型研究

在已有的UHPC中GFRP筋粘结-滑移试验曲线中,仅有绕肋GFRP筋的曲线数据较为完整,故本节基于文献[30]中20根绕肋GFRP筋拉拔试件的粘结-滑移曲线开展理论分析。

由于实际工程受力过程中FRP筋通常不发生粘结破坏,其滑移量只处于粘结-滑移曲线的上升段,且下降段的试验数据较少且较不稳定,因此本文针对粘结-滑移曲线的上升段开展分析。需要说明,本文中的滑移量均指FRP筋自由端的滑移量。

4.1 FRP筋与普通混凝土之间的粘结-滑移本构模型

目前,国内外已有的用于描述普通混凝土中FRP筋粘结-滑移的模型主要包括Malvar模型[11]、CMR模型[12]、mBPE模型[13]和高丹盈模型[36]。

1) Malvar模型[11]。

1994年,Malvar等[11]首先建立了普通混凝土中FRP筋的粘结-滑移模型,该模型采用式(20)预测FRP筋的粘结-滑移全曲线：

(20)

式中：τ和s分别为粘结应力和滑移量;τm和sm分别为峰值粘结应力和相应的滑移量;F和G为通过试验曲线拟合得到的系数。

2)CMR模型[12]。

1995年,为改进Malvar模型,Cosenza等[12]提出了CMR模型,该模型用于描述FRP筋粘结-滑移曲线的上升段,其公式为：

(21)

式中sr和α为通过试验曲线拟合得到的系数。

3)mBPE模型[13]。

1997年,在Eligehausen等[37]建立的用于描述钢筋与普通混凝土之间粘结-滑移曲线的BPE模型的基础上,Cosenza等[13]提出了针对FRP筋与普通混凝土之间粘结-滑移曲线的改进BPE模型(mBPE模型)。该模型上升段的公式为：

(22)

式中β为通过试验曲线拟合得到的系数。

4)高丹盈模型[36]。

2003年,郑州大学的高丹盈[36]提出了FRP筋与普通混凝土之间粘结-滑移的连续曲线模型。该模型只需考虑2个特征参数,具有物理概念明确、曲线光滑连续等优点[36],适用于有限元分析,其上升段的公式为：

(23)

上述模型中,Malvar模型公式形式复杂,且分母中存在未知数,回归得到的曲线可能在上升段中存在奇异点,不便于开展理论分析。故分别采用CMR模型[12]、mBPE模型[13]和高丹盈模型[36],并基于最小残差平方和原则对GFRP筋粘结-滑移曲线的上升段进行回归,得到的理论曲线与试验曲线的对比如图4。可见：CMR模型得到的理论曲线与试验曲线吻合较好,且该模型初始斜率无穷大,与拉拔初始阶段粘结力迅速增加的试验现象相符,故本节基于CMR模型研究绕肋GFRP筋与UHPC之间的粘结-滑移本构模型。

图4 不同模型得到的粘结-滑移理论曲线与试验曲线的对比Fig.4 Comparison of theoretical bond-slip curves calculated from different models with experimental curves

4.2 已有绕肋GFRP筋与UHPC之间粘结-滑移本构模型的理论研究成果

目前,仅有Yoo等[30]针对UHPC中绕肋GFRP筋的粘结-滑移曲线开展了理论研究,其研究结果表明CMR模型相比mBPE模型与试验结果吻合更好,并建议对直径13 mm和16 mm的绕肋GFRP筋,sm分别取1.35 mm和1.51 mm,sr分别取0.16 mm和0.22 mm,α分别取0.5和0.49,τm按式(10)计算。需要说明,文献[30]提出的模型中,存在两方面的问题：1)粘结强度计算公式中未考虑FRP筋表面形态的影响;2)粘结-滑移本构模型中未考虑相对粘结长度的影响。

鉴于此,本文在第2节中提出的粘结强度计算公式的基础上考虑相对粘结长度的影响,并基于CMR模型提出UHPC中绕肋GFRP筋粘结-滑移曲线上升段的计算公式。

4.3 本文提出的绕肋GFRP筋与UHPC之间粘结-滑移本构模型的计算公式

试验表明[30],相对粘结长度Le/db对GFRP筋达到峰值粘结力时相应的滑移量sm无明显影响,通过对文献[30]中的20个试验数据的非线性回归可得：

(24)

式中db和sm的单位均为mm。

基于CMR模型和最小残差平方和原则对上述试件粘结-滑移曲线的上升段进行回归,并进一步以db和Le/db为变量对得到的系数α和sr进行非线性回归,得：

α=0.45

(25)

(26)

式中sr的单位为mm。

Yoo等[30]提出的模型和本文提出的模型与试验曲线的对比如图5,其中本文模型按式(12)和(24)～(26)计算。可见本文模型与试验结果吻合更好。

图5 不同粘结-滑移模型与试验曲线的对比[30]Fig.5 Comparison of different bond-slip models with experimental bond-slip curves

需要说明,由于已有试验数据有限,上述计算公式仅适用于绕肋GFRP筋。其他表面形态的GFRP筋在UHPC中的粘结-滑移曲线有待进一步研究。

5 结论

1)影响GFRP筋与UHPC粘结强度的主要因素包括UHPC抗压强度、相对保护层厚度、试件类型、GFRP筋相对粘结长度及表面形态。其中,GFRP筋与UHPC粘结强度随UHPC抗压强度和相对保护层厚度增大而增大;随GFRP筋相对粘结长度增加而降低;梁式试件测得的粘结强度略高于拉拔试件;螺纹GFRP筋的粘结强度低于绕肋GFRP筋和粘砂GFRP筋。

2)基于统计分析,综合考虑FRP筋表面形态、相对粘结长度、相对保护层厚度、UHPC抗压强度和试验方法的影响,提出了绕肋GFRP筋、螺纹GFRP筋和粘砂GFRP筋与UHPC之间粘结强度的计算公式。与已有公式相比,本文提出的计算公式考虑了FRP筋与UHPC粘结强度的主要影响因素,且与试验结果吻合良好。由于粘结强度变异性较大,故在该公式基础上基于区间预测提出了考虑保证率的粘结强度和锚固长度计算公式,该公式可为工程设计及后续研究提供依据。

3)基于CMR模型提出了绕肋GFRP筋粘结-滑移曲线的上升段的计算公式,得到的理论曲线与试验曲线吻合良好。需要说明,由于下降段曲线的不稳定性及缺乏充分的试验资料,本文未提出UHPC中GFRP筋粘结-滑移曲线下降段的理论公式。