Banach空间中非扩张映射和m-增生算子零点的广义隐黏性迭代方法

潘灵荣, 王元恒

(1.浙江广播电视大学 温岭学院,浙江 温岭 317500; 2.浙江师范大学 数学与计算机科学学院,浙江 金华 321004)

变分不等式理论和不动点理论已经成为解决基础科学和应用科学中许多问题的重要工具,其在信号处理、均衡问题和优化问题中都有广泛的应用,把这些问题转化为不动点问题是很多学者关注的焦点(文献[1-7]).隐中点规则是求解微分代数方程和普通微分方程的重要数值计算方法之一,许多学者运用该方法进行了黏性迭代算法的收敛性分析,详见文献[8-14].

2009年,Chang[15]给出了关于m-增生算子和非扩张映射的黏性迭代算法:

并证明了关于m-增生算子和非扩张映射的序列{xn}强收敛于公共不动点p,这也是下列变分不等式问题的解:

〈(I-f)p,j(x-p)〉≥0,∀x∈F(S)∩N(A).

(1)

2017年,Luo[16]在一致光滑Banach空间中研究了关于非扩张映射的黏性隐式中点法则,迭代算法生成如下:

在适当条件下,证明了该序列强收敛于p∈F(T),这也是下列变分不等式问题的解:

〈(I-f)p,j(x-p)〉≥0,∀x∈F(T).

2018年,Zhang[17]在自反的一致凸Banach空间中研究关于m-增生算子和非扩张映射的黏性隐式中点法则:

证明了该序列强收敛于p∈F(S)∩N(A),也是变分不等式(1)的解.

受以上文献启发,我们在Banach空间中给出关于m-增生算子和非扩张映射的广义隐黏性迭代方法:

(2)

在适当的条件下,证明了该方法生成序列{xn}的强收敛定理,推广和改进了Luo[16]和Zhang[17]的主要结果.

1 预备知识

设E是Banach空间,E*是E的对偶空间,对偶映射J:E→2E*定义为

J(x)=

其中〈·,·〉表示对偶配对.

映射T:C→C称为非扩张映射,若

设F(T)是映射T的不动点集.

映射f:C→C称为压缩映射,若存在k∈[0,1),满足

映射A:C→E称为增生算子,若存在j(x-y)∈J(x-y),满足

〈Ax-Ay,j(x-y)〉≥0,∀x,y∈C.

若对于所有的r>0,R(I+rA)=E,则称A是m-增生算子.我们记Jr=(I+rA)-1(r>0)为A的预解式,N(A)={x∈E:0∈Ax},F(Jr)为Jr的不动点集.众所周知,Jr是非扩张映射且N(A)=F(Jr).

引理1[17]Banach空间E是一致凸的,当且仅当存在一个连续严格递增凸函数g:[0,+∞)→[0,+∞),g(0)=0,使得

(3)

引理2[19]若λ,μ>0,则对x∈E,有

xn+1=Vnxn+(1-Vn)en,

则有

引理4[21]设E是自反的一致凸Banach空间,具有一致G-微分范数,C⊂E是非空闭凸集,具有正规结构.设T:C→C是非扩张映射且F(T)≠∅,f:C→C是压缩映射,定义xv=vf(xv)+(1-v)Txv,v∈(0,1),则序列{xv}在F(T)上强收敛于一点.

引理5[22]设{Cn}是一非负实数列,使得Cn+1≤(1-δn)Cn+δnθn,∀n≥0,其中{δn},{θn}满足:

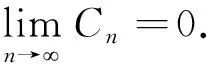
2 主要结论

定理1设E是自反的一致凸Banach空间,具有一致G-微分范数.C⊂E是非空闭凸集且具有正规结构.f:C→C是压缩映射,压缩系数k∈[0,1).A是E中的m-增生算子.T:C→C是非扩张映射且F(S)∩N(A)≠∅.对于任一x0∈C,∀n∈N,序列{xn}由(2)式生成,其中{αn},{βn},{γn},{vn},{μn}和{rn}为(0,1)中的序列,且满足下列条件:

则序列{xn}强收敛于一点p∈F(S)∩N(A),这也是变分不等式问题(1)的解.

证明证明过程分为以下几个步骤.

第一步,证明序列{xn}有界.取p∈F(T)∩N(A),则

由序列{xn}的定义知

移项整理得

所以{xn}是有界的,从而{yn},{un},{Jrnyn},{Jrnxn},{Txn}和{Tyn}是有界的.

从而

(4)

由(2)式可知

(5)

(1-βn)(Jrnun-Jrn-1un-1)+

(6)

(7)

由引理2可知

(8)

由(5)～(8)式可得

移项整理得

(9)

其中

|vn-vn-1|+|μn-μn-1|+2μn|γn-γn-1|+

因此

结合(6)～(8)式,得到

由(9)式得到

其中

由条件(ⅰ)、(ⅲ)、(ⅳ)、(ⅴ)和(4)式可知

(10)

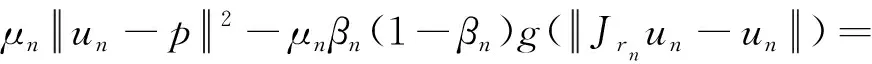
移项整理得

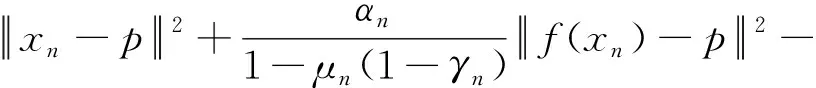
若

则

我们得到

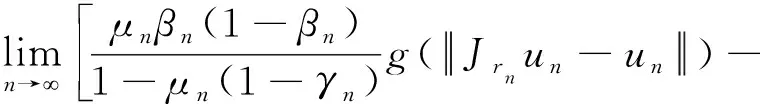
(11)

观察

结合(10)式和(11)式,我们得到

(12)

另外有

(13)

(14)

(15)

由{xn}的定义可知

xn+1-Tyn=αnf(xn)+vnxn+μnTyn-Tyn=

αn(f(xn)-Tyn)+vn(xn-xn+1+xn+1-Tyn),

移项整理得

(16)

而且

结合(10)式、(15)式和(16)式,有

(17)

我们知道T和Jrn是非扩张映射,所以

由(11)式、(13)式、(15)式和(17)式得到

(18)

(19)

根据引理2可知

结合(18)式,有

(20)

由Jr是非扩张映射得到

结合(15)式和(20)式,有

第四步,证明

设xt=tf(xt)+(1-t)Txt,由引理4知,{xt}强收敛到p∈PF(T)∩N(A)f(p),且是变分不等式〈p-f(p),j(p-q)〉≤0,∀q∈F(T)∩N(A)的唯一解.

(1-t)〈Txt-Txn+Txn-xn,j(xt-xn)〉+

t〈f(xt)-xt+xt-xn,j(xt-xn)〉≤

t〈f(xt)-xt,j(xt-xn)〉,

移项整理得

〈xt-f(xt),j(xt-xn)〉≤

由(19)式可知

(21)

第五步,观察

〈αnf(xn)+vnxn+μnTyn-p,j(xn+1-p)〉=

αn〈f(xn)-f(p)+f(p)-p,j(xn+1-p)〉+

vn〈xn-p,j(xn+1-p)〉+

μn〈Tyn-p,j(xn+1-p)〉≤

αnk〈xn-p,j(xn+1-p)〉+

αn〈f(p)-p,j(xn+1-p)〉+

αn〈f(p)-p,j(xn+1-p)〉+

αn〈f(p)-p,j(xn+1-p)〉+

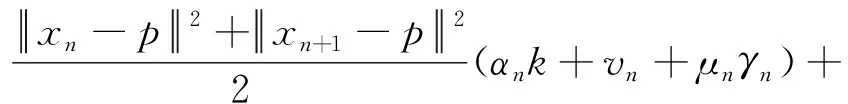
αn〈f(p)-p,j(xn+1-p)〉,

移项合并整理得到

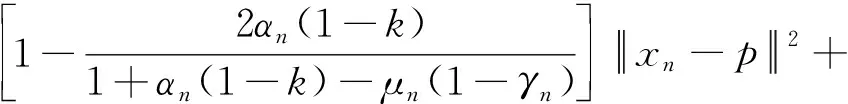
令

由(21)式可得

综上,根据引理5得xn→p.