基于地块概化和路网精细模拟理念的城市雨洪过程分区自适应模型
李东来,侯精明,申若竹,高徐军,3,黄绵松,马 越
(1. 西安理工大学省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048;2. 宁夏首创海绵城市建设发展有限公司,宁夏 固原 756000;3. 中国电建集团西北勘测设计研究院有限公司,陕西 西安 710065;4. 陕西省西咸新区沣西新城开发建设(集团)有限公司海绵城市技术中心,陕西 西安 712000)
全球气候变化引起的极端降雨频发,加之中国快速城市化进程中流域下垫面的显著变化,多种因素叠加导致城市洪涝灾害日益严重[1]。近数十年来,中国各大城市均遭受过不同程度的洪涝灾害,郑州、北京、深圳等多地甚至出现较为严重的人员伤亡[1-2]。城市流域地下管网密布,道路纵横,下垫面条件较为复杂,且部分区域的基础数据不易获取,诸多问题为城市洪涝模拟带来巨大挑战[3-4]。因此,建立适用于不同下垫面条件的城市雨洪模型对探明洪涝致灾机理、评估灾害风险和进行预警预报具有重要意义[4]。
随着洪涝模拟技术的发展和计算能力的提升,城市雨洪模拟方法已从单纯的水文学方法或水动力学方法发展到水文水动力耦合方法[5-7],耦合二维地表模块和一维管网模块的水文水动力耦合模型逐渐成为研究的热点[8-10]。目前有2种水文水动力耦合模式应用最为广泛,张红萍等[8]根据技术策略和降水产汇流计算方式的区别将耦合模式分为半分布耦合模式和全分布耦合模式。半分布耦合模式为水文驱动水动力模型,将整个流域划分为概化子汇水区,雨水通过子汇水区进入管网,只有管道发生溢流时,才驱动二维地表模型进行淹没计算[8-9];全分布耦合模式为全水动力模型,将研究区域划分为二维精细计算单元,降水蒸发等水文过程都在网格单元上实现,地表经过汇流演进后汇入地下管网[8]。半分布耦合模式物理机制不足,径流路径不符合实际物理过程,对于城市道路汇流及低洼区域的淹没计算难以表达;在地块区域地形及管网资料不足情况下,全分布耦合模式忽略了地块中管网排水的作用,进而造成地块低洼区域出现大量积水的不正常现象,且计算量巨大,计算效率极低[11]。目前较为成熟的商业化软件,如MIKE Flood和InfoWorks ICM等均采用半分布耦合模式进行城市雨洪过程模拟[12]。黄国如等[9]耦合了自主研发的二维模型和Storm Water Management Model(SWMM)模型,采用半分布模式模拟了广州东濠涌流域的雨洪过程;Li等[11]将自主研发的二维水动力模型与SWMM模型进行了耦合,采用全分布耦合模式对宁夏固原某区域雨洪过程进行了模拟,但未考虑地块中精细管网的排水作用。
为更好体现城市流域实际的径流过程,王船海等[13]提出了基于雨篦子耦合地表与管网的全过程耦合模型,细化了子流域内产汇流计算方法;Zhang等[14]提出了概念连接和物理连接2种模式的分布式水动力模型,采用概念连接将地块网格与检查井建立联系。对于城市流域,道路低洼点的积水大部分是由道路区域本身径流贡献产生[15],准确反映道路产汇流特性对城市内涝模拟至关重要[16]。此外,地块内部也分布有较多的雨水口和排水管网,以缓解地块区域的内涝积水,其排水作用不可忽略[17-18]。整体区域划分子汇水区时忽略了真实的地形情况,而整体区域划分精细网格则会增加计算量,降低计算效率。
为克服现有数据条件和计算能力的限制,本文基于SWMM模型和GPU加速的二维水动力模型(GAST),提出了基于地块概化模拟和路网精细模拟理念的城市雨洪过程分区自适应模型(以下简称分区模型)。以西咸新区沣西新城核心示范区为研究对象,分别建立区域全分布耦合模型、半分布耦合模型和分区模型,通过对比分析3种耦合模型在不同设计降雨下的内涝积水和管网排水情况,对分区模型在城市雨洪模拟中的应用效果进行评估。
1 研究方法
1.1 汇水区产汇流模型
通过将区域划分成若干概化子汇水区,根据子汇水区的特点单独计算降雨及其产汇流过程,并认为子汇水区产生的径流全部汇入特定雨水口或其他子汇水区中。SWMM作为目前最为常用的降水-径流模型,将单一子流域划分为透水部分和不透水部分,其中不透水部分根据有无洼蓄能力进行再次划分。产流计算时综合考虑填洼、下渗及蒸发等过程,汇流过程采用线性水库法计算。该模型在城市雨洪模拟方面的良好性能已被诸多案例所证实[18],本文采用SWMM模型计算汇水区产汇流过程。
1.2 一维管网模型
求解一维圣维南方程对管网水流运动过程进行精准计算已成为趋势,其中动力波方法物理意义明确,方程求解过程完整,理论上计算结果最为精确,且可以模拟管道逆流、明满流交替运动、水位顶托、进口和出口损失等各种复杂流态和复杂工况,目前已成为管网水流模拟的主流方法。SWMM模型中提供了动力波方法计算管网汇流过程[11],本文采用SWMM模型计算管网水流运动过程。
1.3 二维地表水动力学模型
采用GAST模型[19-21]对地表水动力过程进行计算,GAST模型是西安理工大学开发的地表水及其伴随输移过程数值模型。该模型基于结构网格,采用Godunov格式的有限体积法对二维浅水方程进行数值离散,该类方法能够稳健地解决不连续问题,并可严格保持物质守恒。模型应用了一套能适用于任何复杂网格的二阶算法,提高了模拟的精度和计算效率;底坡源项采用底坡通量法处理,将单元内底坡源项转化为单元边界上的通量,该方法可以严格保持全稳条件[21];摩阻源项采用新的半隐式格式处理,可准确地计算复杂薄层水流运动情况,消除了常规隐式方法冗余迭代,同时兼顾了计算精度和效率[22]。解决了在地表水流动模拟中的一些数值难题,如复杂地形、复杂边界、复杂流态包括干湿交替等。目前该模型已成功应用于城市洪涝[23-24]、溃坝山洪及江河洪水[20]等过程的模拟中,模型精度与模拟效率俱佳。
本文主要对城市流域雨洪过程进行研究,对于一维管网和二维地表的水流交换问题,采用垂向连接的方式进行耦合计算[11]。通过Visual Studio平台调用SWMM动态链接库(DLL)的方式进行耦合交互计算,详细实现过程可见文献[11]。
1.4 分区耦合模式
半分布耦合模式主要将管网作为排水通道排放径流,高估了管网排水的效果,忽略了城市地表漫流过程的影响[8]。此类耦合模式对区域数据精度要求较低,且具有计算速度快的优点。全分布耦合模式径流路径符合实际物理过程,基于精细地表网格,将降水产汇流过程和径流演进过程统一计算,物理机制明确[8]。现有城市流域尺度研究大多仅能体现道路上的雨水管网分布情况,忽略了建筑小区或地块中的雨水管网分布,体现地块内雨水管网分布情况的数据难以获取,即使可以获取,如此精细管网建模的工作量也将非常大。若在城市流域尺度进行如此精细模拟势必带来巨大的计算量,严重影响计算效率[9]。
结合以上2种耦合方式的特点,提出了基于地块概化模拟和路网精细模拟理念的城市雨洪过程分区自适应耦合模式,在资料充足的道路区域采用划分精细网格的水动力方法,对于资料不足的地块区域采用划分子汇水区的水文概化方法。分区模型主要由概化子汇水区模块、二维地表模块和管网汇流模块3部分组成(图1)。建模时根据地形及下垫面属性将研究区域划分为2类区域,一类如城市道路等自身产汇流过程对内涝形成影响显著的区域;一类为建筑小区等地块区域,区域内管网数据难以获取。在道路区域进行网格剖分建立地表模型,在地块区域划分子汇水区建立概化模型;同时,构建包括雨水口的管网模型,建立雨水节点与地表网格和子汇水区的对应关系。该耦合模式的径流路径为:① 同时在二维地表模型和概化子汇水区上进行降水和产汇流计算;② 将二维地表模型和概化子汇水中产生的水量输入各自连接的雨水口中;③ 管网模型进行汇流演进计算。分区模型的耦合模式和径流过程如图1所示。此耦合模式结合了半分布耦合模式和全分布耦合模式的优点,既克服了地块中管网数据难以获取的困难,又减少地表模型的计算量,且整体径流路径与实际物理过程一致。
分区自适应耦合方法不仅适用于概化地块和精细路网,也可根据城市流域不同的数据条件、关注程度和洪涝范围自适应确定概化模拟区域和精细模拟区域。随着计算能力的提升和数据采集技术的发展,当整个城市流域都具有精细地形和管网数据时,可将整个区域都离散为二维精细网格进行计算。城市一些区域资料不足,或为了提升计算效率,则可考虑对某些区域进行概化模拟。分区自适应耦合模式有效解决了数据条件和计算能力的矛盾,可为城市洪涝模拟提供一种新的耦合思路。
分区耦合模式未考虑概化地块与精细路网通过地表通道的交互过程,如何确定地块与邻近道路的交互量是问题的关键,后续拟结合物理试验进行深入研究;该耦合模式仅考虑由降水引起的内涝积水过程,对于外江或山洪引起的城市大范围淹没过程适用性不足,此情形需将整体区域均划分为精细网格;对于地块占比较大、道路占比较少的城市老城区,单纯基于地块和路网进行分区可能不再适用,需根据实际径流过程和既有数据进行重新分区。
2 研究数据
2.1 研究区概况
陕西省西咸新区沣西新城位于西安市以西、咸阳市建成区以南、渭河以东、沣河以西。根据秦都区国家基本气象站近30 a(1981—2010年)的逐月降水量数据统计,新城多年平均降水量约520 mm,其中,5—10月降水量较多,7—9月份降水量最大,且夏季降水多以暴雨形式出现,为半湿润大陆性季风气候,易发生内涝灾害[18]。本次选取研究区域为沣西新城核心示范区,隶属3号排水分区内,区域范围及位置如图2所示,该区域占地面积为3 km2,是集中各种优势资源重点建设区域。研究区域内道路低洼地段较多,遭遇强降雨时极易产生大面积道路积水。

图2 研究区域位置示意Fig.2 Location of study area
2.2 基础资料
城市雨洪模型建模所需的基本数据主要包括地形、排水管网分布、土地利用、降雨与下渗等。
(1) 地形与影像数据。采用激光雷达与高清相机采集了研究区域的数字高程模型(DEM)和影像数据,并将DEM处理成分辨率为2 m×2 m结构网格,研究区域DEM数据及影像数据如图3所示。
(2) 土地利用数据。根据研究区域正射影像图将下垫面划分为绿廊区域、道路、硬化地面、建筑物、草地、林地和裸地7种土地利用类型,具体划分情况如图3(c)所示。每种土地利用的曼宁糙率参照城市排涝相关标准及文献确定[25],假定草地、林地、裸地为完全透水,道路、硬化地面、建筑物为完全不透水,并据此确定子汇水区中的不透水情况,具体参数如表1所示。
(3) 排水管网。管网模型建模所需的基础数据主要包括雨水口位置、井底高程,以及管道走向、管径与形状等。本文主干管道数据由沣西新城管委会提供,雨水口具体位置经现场实测获取,研究区域管网具体分布如图3(b)所示,区域内共有雨水节点576个,雨水管道577条。
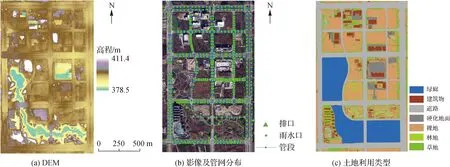
图3 研究区域基础信息Fig.3 Basic information of study area
设计降雨:根据咸阳气象站30 a以上实测降水数据推求沣西新城设计暴雨,暴雨强度计算公式[18]如下所示:
(1)
式中:q为设计暴雨强度,mm/min;P为重现期,a;t为降雨历时,min。计算得到重现期为2、5、30、50和100 a的历时120 min的设计降雨,各重现期暴雨过程如图4所示。

图4 不同重现期设计暴雨Fig.4 Hyetography of the design storms with different return periods

表1 下垫面属性及参数取值
3 模拟结果及分析
3.1 模型构建
根据研究区域地形、土地利用、道路和排水管网分布,构建半分布模型、全分布模型和分区模型。因该研究区域道路存在低洼点,地块内无内涝积水情况发生,故分区模型仅对道路区域进行网格剖分,其他区域采用概化子汇水区形式进行计算。在3种耦合模型中均将绿廊区域概化为调蓄措施,并将排入绿廊的排口接入到蓄水设施中。因该研究区域尚在建设中,区域内设计了诸多低影响开发措施,本文将区域视为常规区域,暂不考虑低影响开发的布设情况。
3种耦合模型中管网概化情况一致,均为576个雨水口、1个排水口、1个蓄水设施和577段管道,概化子汇水区和地表网格划分情况有所区别。因研究区域雨水口分布较多,故采用泰森多边形法对汇水区进行划分[26]。半分布模型中将整个区域划分为1 031个概化子汇水区,地表网格数为532 415个;全分布模型中无概化子汇水区,地表网格划分情况与半分布模型一致;分区模型将地块划分为455个子汇水区,206 705个地表网格。3种耦合模型的建模情况如图5所示。

图5 模型概化Fig.5 Sketch of model generalization
3.2 模拟验证
选用2016年8月25日场次降水内涝过程对模型进行验证,气象站位于西咸新区西部云谷小区10号楼,距离研究区域上边界约1 km。该场次降水历时为7 h,累计降水量达66 mm,为双峰雨型,降水强度峰值出现于3.1 h(图6),经降水重现期关系曲线推算该场次降水重现期为50年一遇。

图6 实测降水过程Fig.6 Measured rainfall process
由于当时研究区域处于开发状态,地块和区域管网建设尚未全部完成,故采用全分布模型对该场次雨洪过程进行模拟验证。图7中标记出内涝影响较为严重且有实测数据的4处积水点(t=5 h),通过人工现场测量并在图纸上绘制积水范围后确定实测积水面积。由图7及表2可以看出模拟积水的位置与内涝发生位置吻合,各点积水程度与实测数据相近,其中内涝积水面积平均相对误差均小于3%。对比结果表明模拟的城市内涝积水程度与实际监测积水范围相符,模拟效果较好。
通过现场勘查发现,本次内涝积水主要原因为下游管网施工尚未打通,降水发生时道路及周边雨水汇集到低洼处难以通过管网排出,模型验证过程综合考虑了该实际情况。后续在不同设计降雨中计算时,将管网模型设置为自由出流情况,并以全分布模型结果为准对不同耦合方式模拟效果进行对比。
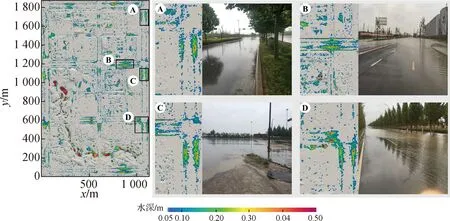
图7 模拟积水情况与实测积水对比Fig.7 Comparison of the simulated and measured inundation

表2 模拟积水面积与实测情况对比
3.3 内涝积水过程
3种耦合模型在不同设计暴雨下的内涝积水面积过程如图8所示。在小于5年一遇降水时,管网足以应对区域的暴雨,半分布模型地表积水基本为0;因道路存在低洼区域和雨水口覆盖不到的区域,降水时会存在洼地积水,全分布模型和分区模型均可刻画这一现象,并且两者模拟结果基本一致。当降水超过30年一遇时,因排水能力不足和地形低洼引起的内涝积水情况增多,可以看出,分区模型模拟结果内涝积水最多,其次是全分布模型,半分布模型模拟出的内涝积水最少。此外,相较于全分布模型,半分布模型峰值存在明显延迟。
图9展示了P=30 a和P=100 a设计暴雨下研究区域内涝淹没和流速分布情况。可以看出,分区模型模拟结果中既存在因地势低洼引起的内涝积水,也存在因管网排水能力不足导致溢流引起的内涝积水,故分区模型内涝积水峰值最大。半分布模型中的积水均由于管道溢流产生,雨水降落到子汇水区再经过管道汇流后通过雨水节点溢流到地表,故存在径流延迟现象。通过对比不同模型内涝积水可以看出,采用全分布模型和半分布模型模拟出的内涝积水点并不一致。全分布模型模拟出了道路低洼区域的积水情况,未产生倒灌,主要原因在于地形采集时,区域内处于建设中,在地块内存在诸多基坑,在地块内的降水大多汇入的基坑中,造成地块内产生了大量积水的不正常现象,未产生道路径流。而半分布模型将管道作为主要的径流通道,认为汇水区产生的径流全部汇入管网,加重了下游管网的排水负担,致使在管网低点处产生溢流。分区模型既考虑了地块向管网汇流的作用,也考虑了地形低洼的作用,将以上2种因素产生的内涝积水情况都表现了出来。分区模型既可以模拟出道路降水径流填洼的实际物理过程,又可以表现管道排水能力不足产生溢流淹没的过程,符合实际物理径流规律,从理论上更为合理。

图8 不同重现期暴雨下3种耦合模型道路积水面积过程Fig.8 Inundation area process of road in three coupled models under the stormwater with different return periods

图9 研究区域水深淹没和流速分布图(t=1.5 h)Fig.9 Water depth inundation and velocity distribution in the study area (t=1.5 h)
3.4 管网排水过程
3种模型在不同设计降雨下的管网排水过程如图10所示,结果表明,在不同降雨下,半分布模型排口流量峰值最大,且峰现时间最靠前;全分布模型排口流量峰值最小,且峰现时间最靠后;分区模型排口流量峰值和峰现时间均在半分布模型和全分布模型之间。可以看出,分区耦合模式考虑了地块内部排水的作用,径流峰值要高于全分布模型;半分布模型认为无论地块和道路上的径流全部汇入管网中,产生的峰值最大,并且模拟结果受参数取值影响较大。
3.5 模拟效率
文中不同设计降雨计算时长为6 h,均在单机上进行模拟计算,计算机配置为Intel(R) Core(TM) i7-8700 CPU @ 3.20GHz型号的CPU和NVIDIA GeForce RTX 2080型号的GPU。不同设计降雨下计算耗时如图11所示,3种耦合模型模拟耗时均随降雨重现期的增加而增加;相较于全分布模型,半分布模型在不同设计降雨下可减少76.4%~88.6%的计算时间,分区模型可减少28.2%~73.5%的计算时间,且均随着降雨重现期的增加而减小。且在P>30 a设计暴雨时,分区模型产生的地表积水较多,进一步增加了计算耗时,故在大重现期下计算效率增速有所降低。可见,分区模型在保证计算精度的同时提高了计算效率,可为城市雨洪过程模拟提供新的耦合计算方法。

图11 不同设计降雨的计算耗时Fig.11 Calculation time of flood simulations at different return periods
4 结 论
本文构建了耦合GAST模型和SWMM模型的水文水动力数值模型,提出了基于地块概化和路网精细模拟理念的分区自适应模型。以西咸新区沣西新城核心示范区为研究对象,构建了研究区域全分布模型、半分布模型和分区模型,模拟了区域不同设计暴雨下的降水径流过程。主要结论如下:
(1) 提出了基于地块概化和路网精细模拟理念的城市雨洪过程分区自适应模型,根据城市不同区域的数据条件和产汇流特性自适应选择相应计算方法,在缺乏精细管网数据的地块采用概化计算方法,在道路区域采用全水动力计算方法。
(2) 在沣西新城核心示范区实际案例中,降雨重现期小于5 a时,分区模型和全分布模型的道路积水过程基本一致,半分布模型并未产生明显的道路积水;在降雨重现期超过30 a时,在地表产汇流和管网溢流共同作用下,分区模型计算出的道路积水面积大于另外2种耦合模型;在不同设计降雨下,分区模型管网排水过程的径流峰值大于全分布模型,小于半分布模型,峰现时间则相反。
(3) 相较于全分布模型,在不同设计降雨下分区模型可减少28.2%~73.5%的计算时间,在保证计算精度的同时显著提高了计算效率。

