基于PSO-DE-BP的光伏发电功率短期预测
刘春芳,王攀攀,曹 菲
(1.南瑞集团(国网电力科学研究院)有限公司,南京 211106;2.江苏林洋新能源科技有限公司,南京 210019)
0 引言
光伏发电技术是当前利用太阳能的主要技术。然而,受天气情况、太阳辐射强度、温度、湿度、云量等影响因素,光伏发电技术有着间歇性、波动性、随机性特点[1],对智能电网的稳定运行带来极大挑战[2]。因此,需要对光伏发电功率预测进行研究,预先得知日内光伏发电功率曲线,使电力部门能以经济最优化调度机组[3],获取最大经济效益。
光伏发电预测技术一直是国内外专家学者研究的热门课题。目前光伏发电预测方式主要分为直接预测和间接预测。间接预测方式是先对地表辐射强度进行预测,然后根据光伏发电模型得到光伏发电功率[4]。文献[5]采用了间接预测,根据历史的光照强度、温度等因素,利用支持向量机的方法来预测光照强度及温度,再通过数学模型得出光伏发电功率,但是未对天气类型分类,精度不高。间接预测过度依赖于复杂的太阳辐射强度模型,对含有不同类型光伏发电单元的系统来说,转换效率、安装角度等参数存在差异。直接预测即直接对光伏电站的输出功率进行预测,常用方法有支持向量机(SVM)[6]、时间序列法[7]、小波分析预测法[8-9]以及人工神经网络法[10-11]。文献[10-11]综合考虑了影响因素,基于神经网络对光伏发电功率提前一天进行预测,误差较大,容易陷入局部最优。文献[12]基于差分进化优化BP神经网络对光伏发电功率预测,有较好的实用性和可行性,但BP神经网络算法具有参数随机初始化、预测系统不稳定以及收敛速度慢等特点,因此会出现早熟现象。
综合以上分析,文章分析光伏发电的影响因素,通过带权重的欧式距离公式筛选出相似样本集;设计PSO-DE-BP混合算法对神经网络进行训练;基于SPARK的平台对PSO-DE-BP并行计算;通过实测数据仿真验证表明,PSO-DE-BP算法比PSO-BP、BP算法精度更好且更稳定,同时,该方法具有良好的并行性能。
1 相似样本集筛选
1.1 影响因子分析
单位面积的光伏发电系统输出功率的数学模型[13]
Ppv_out=ηSI[1-0.005(t0+25)]
(1)
其中:η是光伏阵列转换效率;S是光伏阵列的面积,m2;I太阳辐射强度,kW/m2;t0环境温度,℃。
在固定的光伏发电系统中,光伏阵列的面积是不变的,在一个短期的输出功率预测模型中,光伏阵列转换效率也基本上不变,根据公式(1)的功率输出模型可知,光伏发电功率主要的影响因素就是温度和太阳的辐射强度,根据目前气象局提供的天气信息,尽管缺乏太阳辐射强度的信息,但是气象局提供的天气、云量、湿度以及温度能反应光照辐射强度[14]。
图1为同一光伏电站不同天气类型下光伏发电功率对比曲线。天气类型对光伏发电系统输出功率影响非常明显,且雨天和晴天输出功率值差距很大,表明太阳辐射强度对光伏发电功率影响巨大。
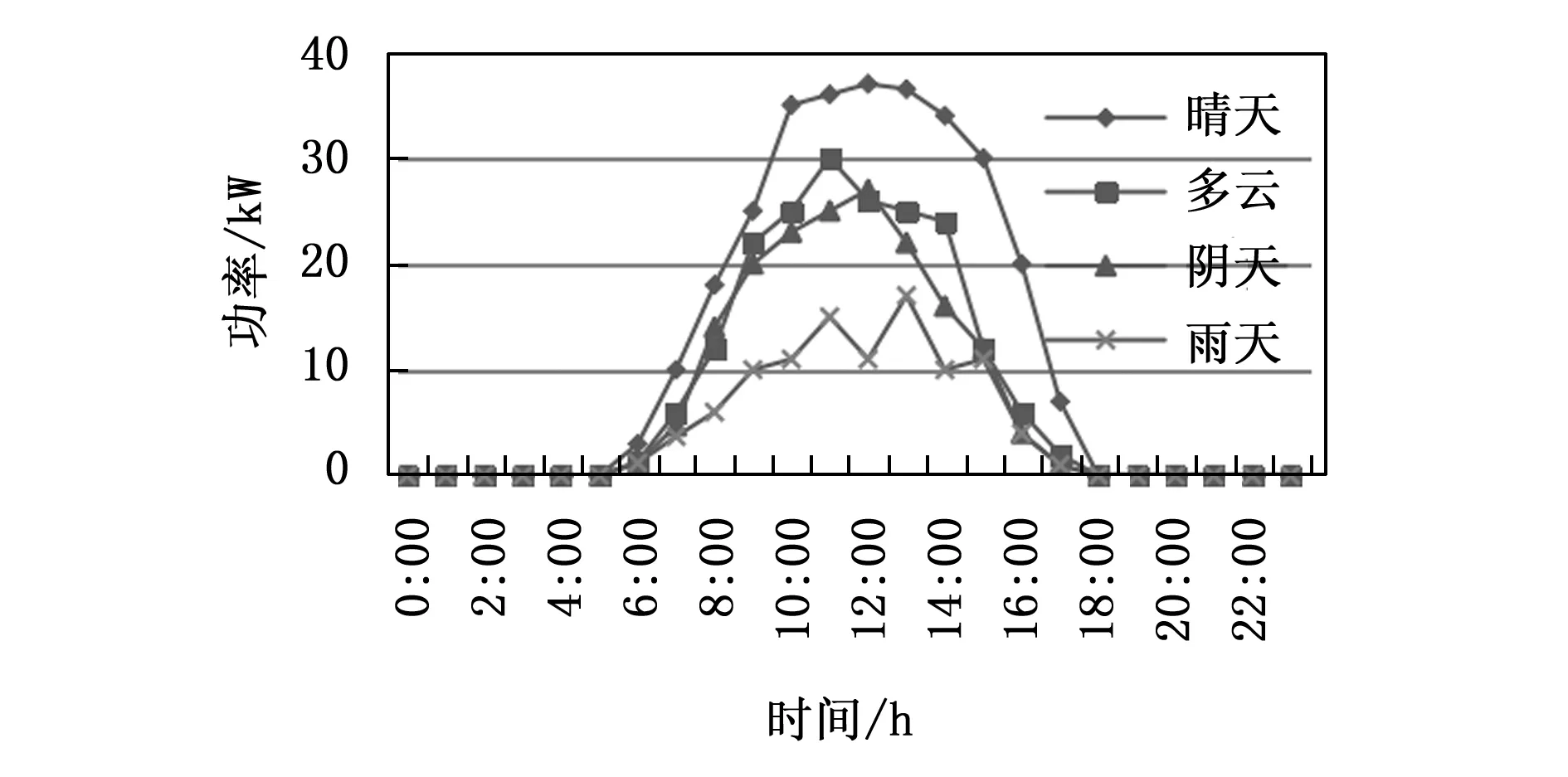
图1 不同天气类型光伏功率输出曲线
表1选取2021年中江苏省某个光伏发电站相同天气类型,不同温度的历史数据,分析温度与日光伏发电量的关系。
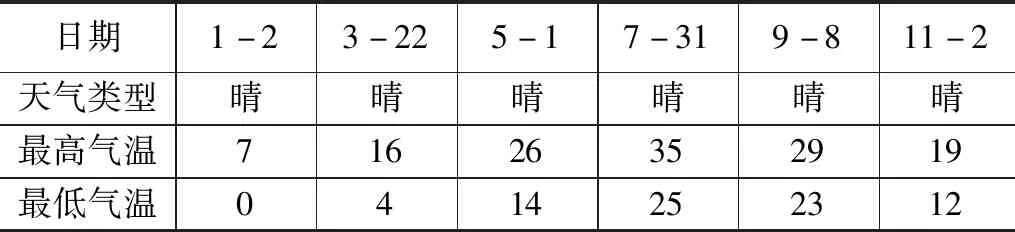
表1 温度气象信息/℃
图2表明,温度与光伏发电先呈现正相关,随着温度的升高,光伏发电量增高,因此,光伏发电功率呈现出随季节的周期性变化。
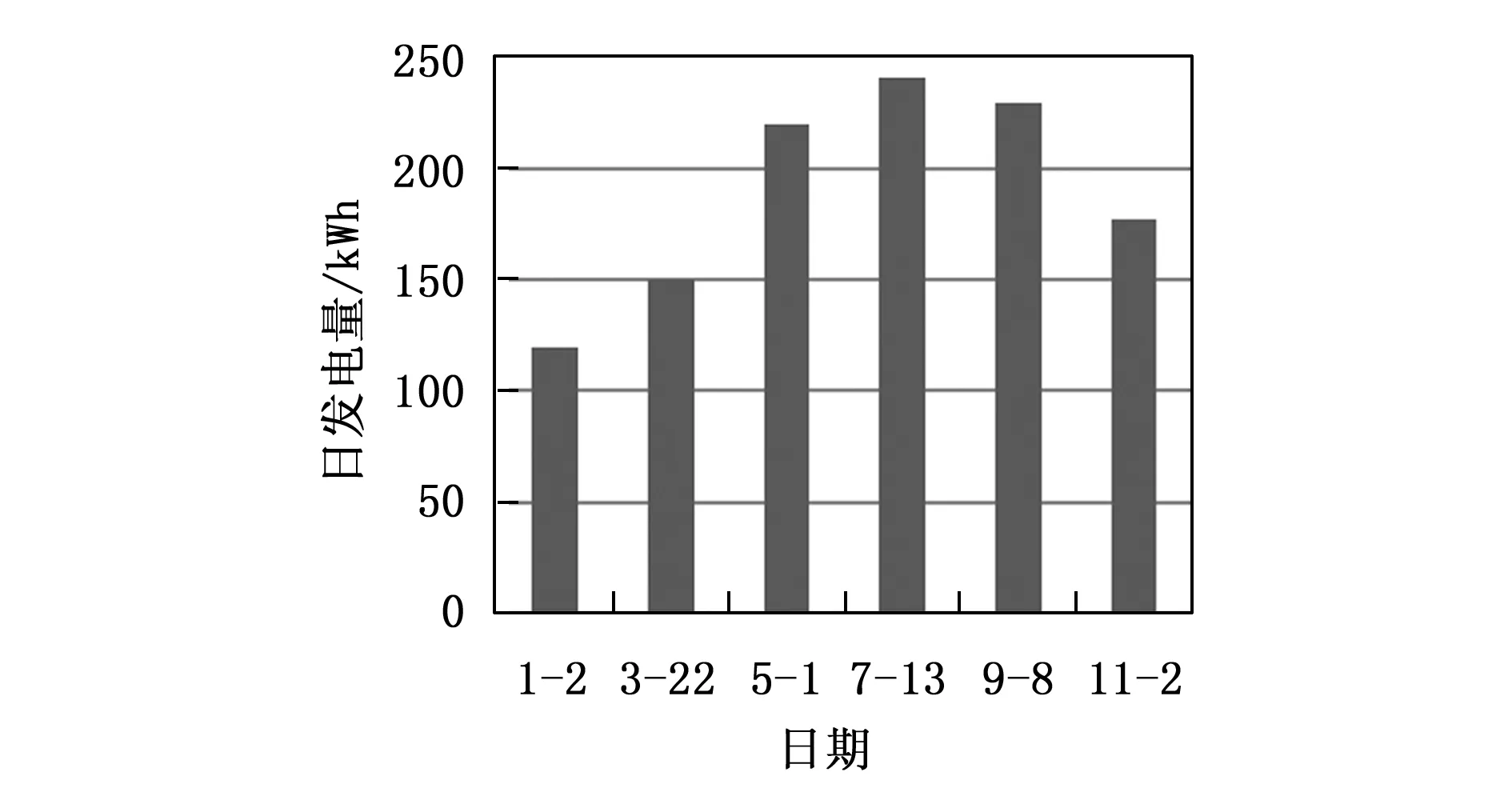
图2 不同的温度下光伏日发电量
表2选择比较相邻几天且来自于同一个光伏发电站的历史数据,天气类型相同,但相对湿度不同。

表2 湿度气象信息
根据图3可知空气湿度明显影响着光伏发电系统的输出功率,湿度越大,光伏输出功率越小,呈现负相关状态,这是由于空气中的液态水能大量吸收太阳辐射能。
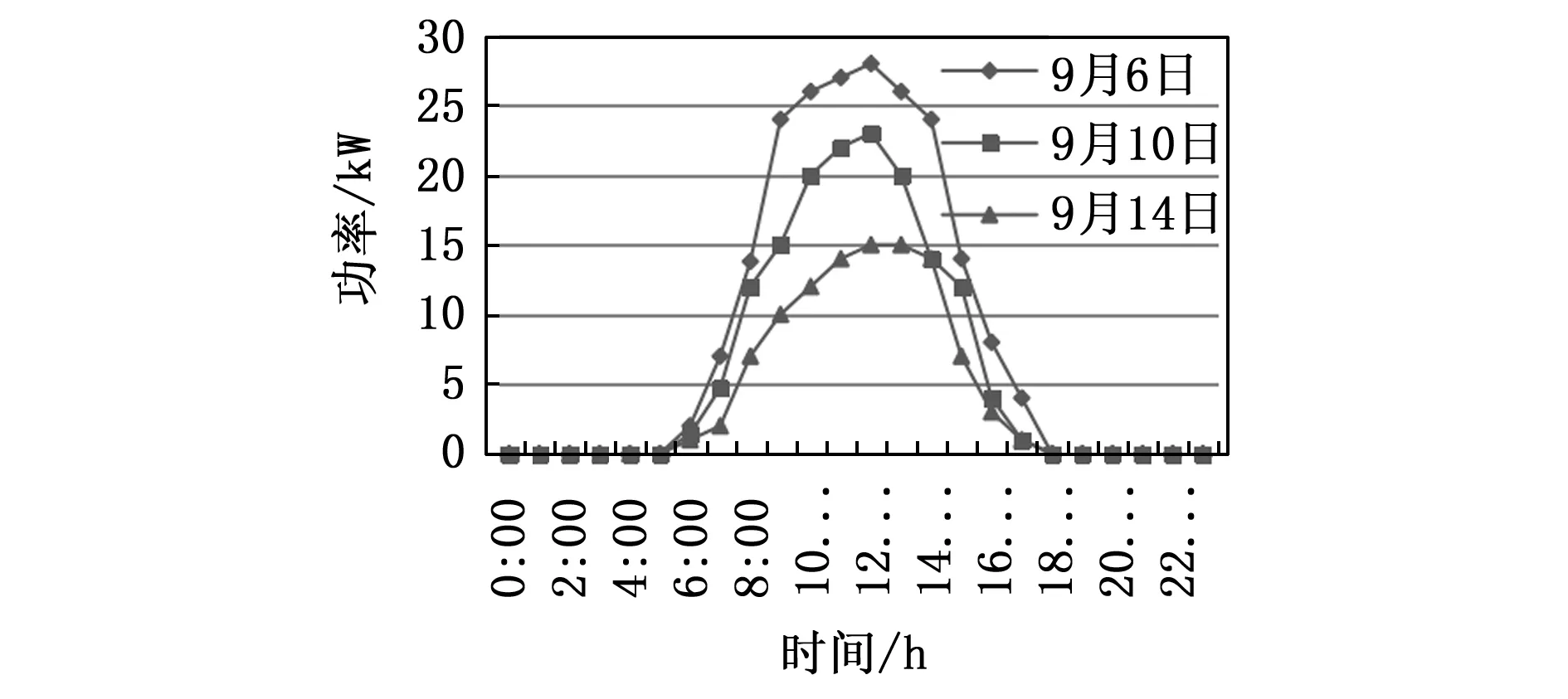
图3 不同湿度下光伏发电功率变化曲线
表3中选取了2021年8月份的气象数据,样本具有相近的温度以及不同的云量。结合图4表明,云量和湿度相似,与光伏发电呈现负相关。由于云将太阳辐射进行反射及散射,大量削弱了太阳辐射强度。因此,云量对预测每个小时的发电功率预测有着重要意义。

表3 云量气象信息
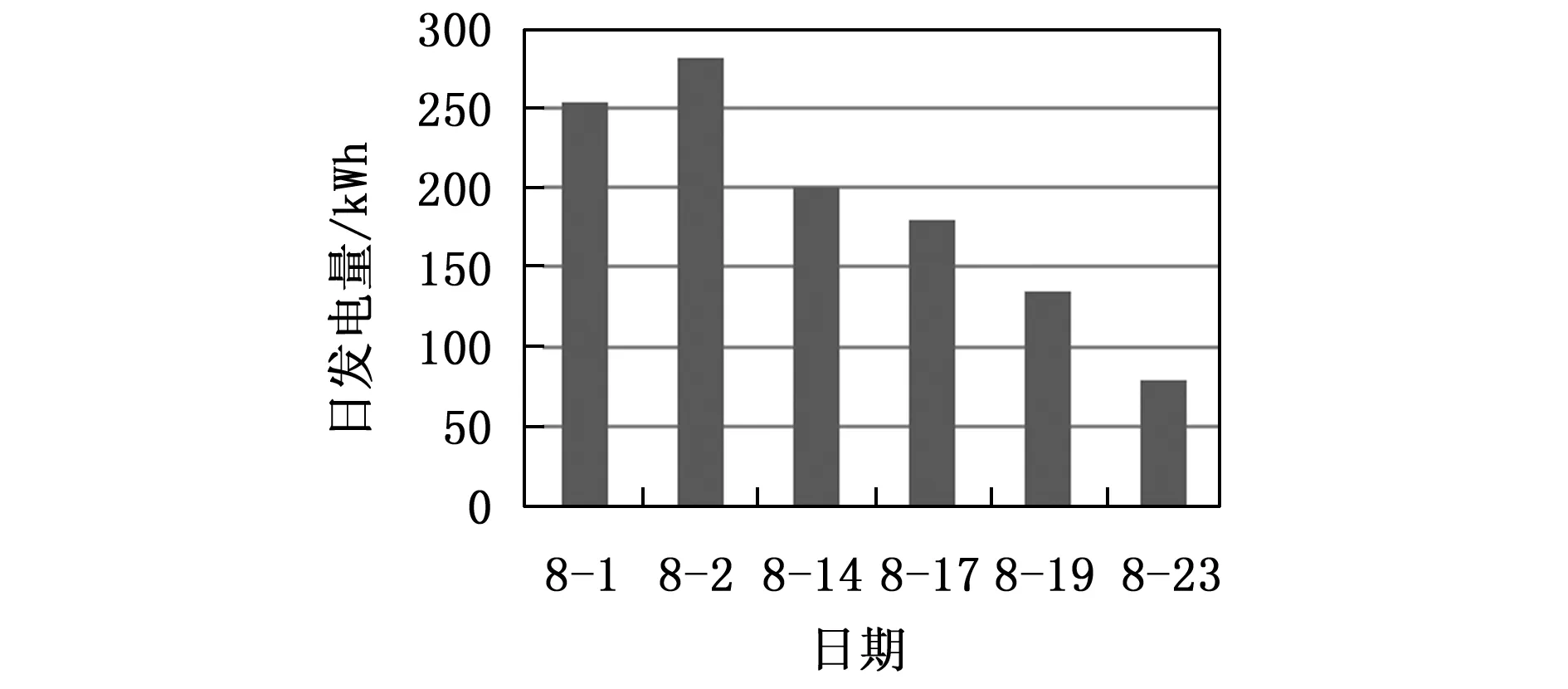
图4 云量与光伏发电量
上述分析可知,光伏发电系统与天气类型、温度、湿度有着密切的关系,但每种因素与光伏发电功率关联度有所不同,因此需要进一步分析影响因子的重要度。
1.2 相似样本选择算法
根据1.1可知,影响因子的差距越大,光伏发电系统的输出功率大小值和变化趋势差距越大。图1可知,在晴天时的输出功率基本呈现上升、保持、下降的变化趋势。然而在阴天、雨天,这种变化过程被破坏[10],输出功率曲线不稳定。文献[15-16]没有筛选相似的训练样本,在阴天或雨天时,功率预测的误差较大。文献[10]基于相似样本,用相似样本集进行训练和预测,减少一定的预测误差,但是只考虑了温度,缺少天气情况作为相似参考量。
然而,影响因子对光伏发电功率的影响程度不同。为了从光伏发电系统历史记录中选择出相似样本集,有效减少预测范围,提高预测精度,通过公式(2)得出各个因子的相关系数[17]。
(2)
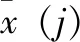
其中,wi表示i影响因子的权重。
(3)
若待预测日的气象特征向量记作x0,x0=[x01,x02,x03,x04],第j个历史日的气象特征向量为xj,xj=[xj1,xj2,xj3,xj4],其中x01,x02,x03,x04分别代表待预测日的归一化后最高温度,最低温度,最高湿度,最低湿度,同理xj中元素也代表4个影响因素。
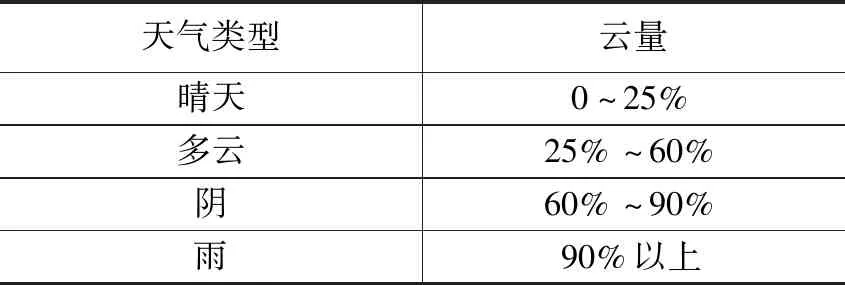
表4 云量与天气类型关系表

表5 BP神经网络输入输出变量

表6 Spark的基本操作
选择相似样本集步骤如下:
1)选择出和预测日相同天气情况m个历史样本,记作Y样本集。
2)由Y样本集用计算公式(2),(3)得出各个影响因子的权重值。
3)计算预测日和样本集Y中历史记录的影响因素的欧式距离di,di的计算公式如下:
(4)
4)将影响因素欧式距离集[d1,d2,...,dm]按距离值的大小升序排序,排列前N个历史样本形成训练样本集YN。
2 BP神经网络预测模型设计
2.1 BP神经网络
BP神经网络是目前使用广泛的神经网络算法之一。如图5所示,典型的神经网络一般有输入层、隐含层、输出层。
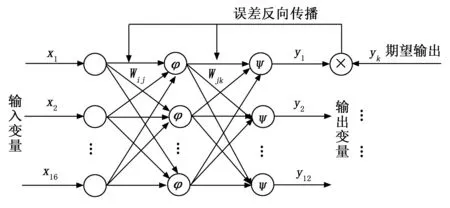
图5 神经网络模型
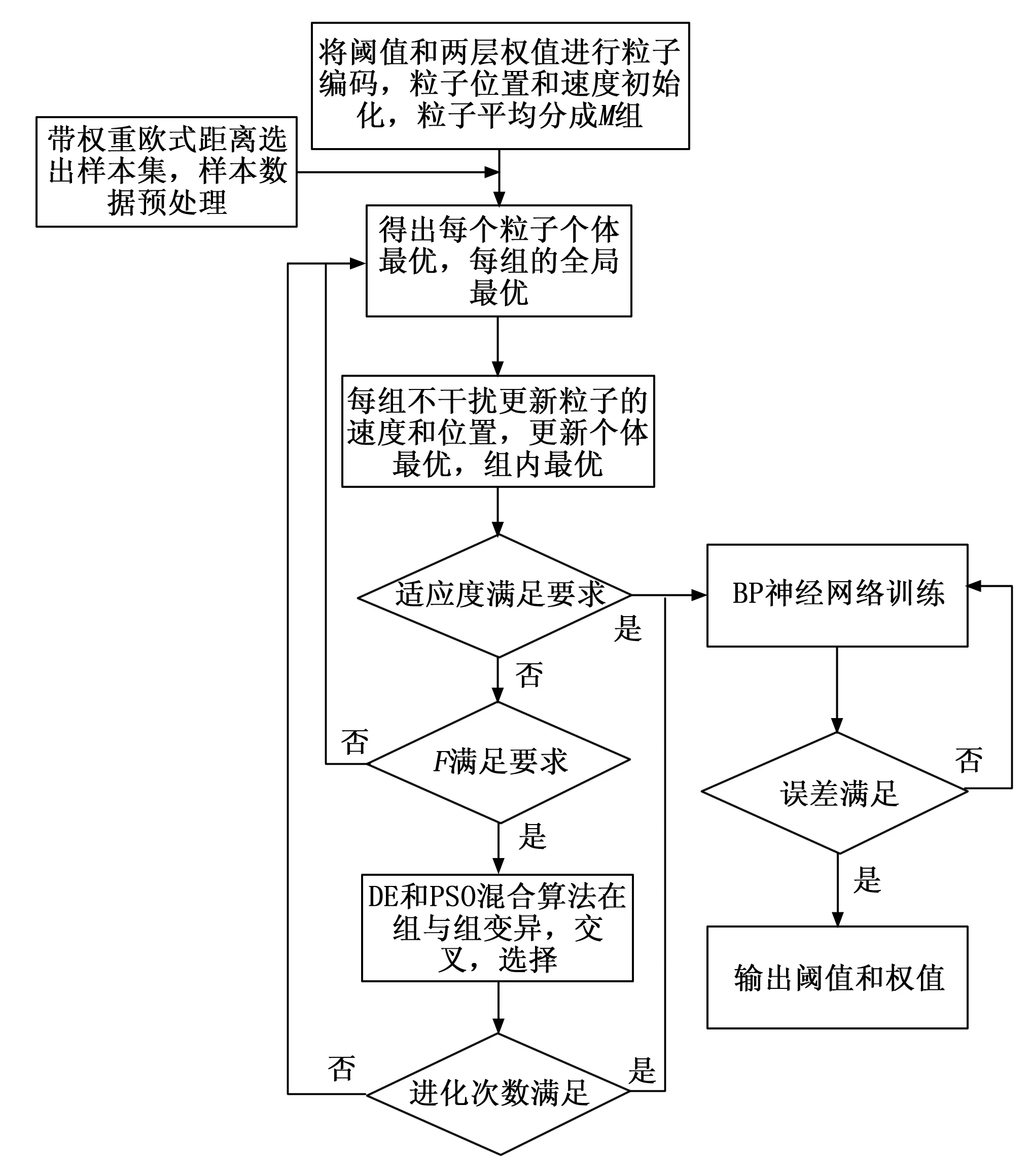
图6 PSO-DE-BP算法优化神经网络流程图
2.2 预测模型建立
2.2.1 BP神经网络输入层确定
光伏发电系统每天主要出力时间段为6:00~18:00。由1节可知,天气类型严重影响光伏发电,即使选择了相同天气的样本集,比如,有着相同的晴转多云的天气类型,但是12个时间点有着不同天气类型。由表4可知,云量能体现各个时间段的天气类型[18],因此,以预测日6:00~18:00的每小时云量、最高温度、最低温度、最高湿度、最低湿度作为输入变量。
2.2.2 输出层节点数
输出层节点为预测日6:00~18:00的每个小时共12个时间段的光伏发电功率。
2.2.3 隐含层节点设计
隐含层节点过多、过少或训练时间过长以及精度不高都对网络的训练不利。充分考虑时间和精度,根据经验公式(5)进行设计[19]:
(5)
式中,I是输入层节点数;O为输出层节点数;J是隐含层节点数;a为1~10的常数。
通过反复调试神经网络模型,充分考虑时间和精度,隐含层选择为10个。
2.3 训练样本预处理
直接用原始的数据作为网络的输入与输出,会引起神经元过饱和。因此,神经网络中输入节点和输出节点的数据都必须归一化处理。通常BP神经网络使用Sigmoid函数,输出范围限定在[0,1]。用公式(6)对1.2筛选出待预测日训练样本集YN做归一化处理,所有数据包括功率数据,影响因素数据都转换到[0,1]区间。
j=1,2…21
(6)
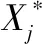
输出样本反归一化:
k=1,2…12
(7)
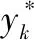
3 PSO-DE-BP混合算法优化神经网络
3.1 基本的粒子群算法和差分进化算法
1)粒子群算法[20]通过粒子的相互作用,对空间任何区域进行智能搜索。主要思想通过群体之间相互协作和信息带有记忆功能及共享信息,寻找最优解。粒子的位置向量代表空间的一组解向量,初始化时,每个粒子都有随机的飞行方向,以一定的速度寻找最优解。由于粒子共享信息功能,粒子的位置、飞行速度大小和方向都随经验动态调整。
粒子速度更新公式:
(8)
粒子位置更新公式:
(9)
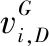
2)差分进化算法是基于群体智能的随机并行优化算法[21],DE拥有记忆功能使其可以动态跟踪当前的搜索情况,以调整策略,寻找最优解。它的优化机制是根据不同个体之间的距离和方向信息来生成新的候选个体,实现群体进化。主要采用变异、交叉、选择3种方式,以这种顺序动态改变个体的位置,寻找最优个体。
变异:
Vi,D,G+1=Xh,D,G+F×(Xr,D,G-Xk,D,G)
(10)
其中:Xh,D,G,Xr,D,G,Xk,D,G是随机选择的个体,且i≠h≠r≠k;Vi,G+1是第i个体的新个体;F是变异算子,属于[0,2]的一个常数;D是维数,优化参数个数;G表示代数。
交叉:
(11)
式中,Vi,D,G+1变异后的i个体;Xi,D,G原个体;CR是交叉率;Ir是[0,D]的随机整数。
选择:贪婪策略选择后代。
(12)
式中,f是适应度函数。
3.2 PSO-DE-BP混合算法优化神经网路
根据2节设计的神经网络模型,用基于PSO-DE-BP的算法优化神经网络训练。BP算法本质是梯度下降法,由前面可知,输入输出变量较多,目标函数比较复杂,容易陷入局部最优,不稳定,且波动性较大。本章节采用PSO-DE-BP混合算法优化RBF神经网络,通过粒子分群组,引入公式(13)保证群组内多样性,运用改进DE的变异操作及选择操作,使组与组之间保持关联,寻找全局最优,避免局部最优。
具体步骤如下。
步骤1:随机初始化粒子xi,D,把神经网络需要优化的权值和阈值使其对应,进行编码,确定目标适应度值E,适应度函数f1,群组之间变异次数G,随机初始化粒子v。
步骤2:将粒子随机平均分成m群,对群体进行编号ID;
步骤3:每组个体根据粒子群迭代的算法,寻找群内最优,达到函数f2目标值,返回各组的群组最优值Xbest,D,g(ID),根据Xbest,D,g(ID)适应度的值大小,m/2组为较好群体,其他的m/2为较差群体。
粒子群迭代的目标函数:
(13)
f2函数的目标值的设定:
F=λ0e(λmax-(λmax-λmin)*(g/G))
(14)
其中:g是当前变异次数;λ0是常数。
F的值随着g次数增大,自适应地改变,粒子群开始,F较大,注重粒子群组之间交叉变异,在保重粒子多样性同时,向较好群体的方向进化,避免局部最优。
步骤4:较好群体之间变异,较差群体往较好群体进化,用DE和PSO混合算法对粒子变异。
改进的变异操作:
vi,D,g-1(ID)=W*vi,D,g(ID)+F1×(rand(Xbest)-Xi,D,G(ID))+F2×(Xbest,D,g(ID)-Xi,D,G(ID))
(15)
Vi,D,g+1(ID)=Xi,D,G+vi,D,g+1(ID)
(16)
(17)
式中,ID是群组号,范围[1,m];i代表ID群i个体;rand(Xbest)表示在较好的m/2个群组当中某个组最优值,随机选取,共m/2个;Xbest,D,g(ID)当前群组最优个体;f(ID)当前群组最优适应度;fbest最优群组的适应度;F2是0到1的随机数。
步骤5:每个群体中个体用公式(11)进行交叉,然后在改进的选择策略上选择下一代个体,避免贪婪策略出现早熟现象。
改进的选择操作:
(18)
(19)
式中,f是适应度函数,R是[0,1]上的随机数。
步骤6:判断是否达到进化次数或适应度目标值,是,停止进化,进入BP神经算法优化,否则转到步骤3。
适应度函数用训练样本的平均均方误差,如公式(20)所示:
(20)
式中,A是实际值;P是预测值,由两层的权值和阈值以及sigmoid函数得出。
4 Spark平台下PSO-DE-BP算法并行优化
随着光伏发电历史数据量快速增长,尽管大量的数据能保证光伏发电功率预测的精度,但是基于单节点难以处理大数据的需要[22-23]。本章节基于Spark平台下,研究PSO-DE-BP算法并行化。
在分布式内存计算框架Spark上进行运算,RDD的数据集格式表示为[24]:
(ZID,ID,x,v,F(ph,fh),(pb,fb),pfm/2,D+1)
其中:ZID是群编号;ID是群组编号;x,v分别表示粒子当前位置向量和速度向量,F为当前目标函数f2的值,ph,fh分别表示为个体经历的最佳位置和最佳适应度;pb,fb分别表示子群组中粒子经历的最佳位置和群组最佳适应度,pfm/2,j是存放较好m/2群组的最佳位置和最佳适应度的m/2×(D+1)矩阵,表示需要优化参数个数和一个适应度。
PSO-DE-BP算法并行化的具体步骤如下:
1)初始化粒子群,包括初始位置和初始速度,差分进化次数,随机对粒子群平均分成M组,并且对群组进行ID编号。
2)以ID编号为key值,其他数据为value,进行Map操作,通过映射函数(20)获得每一个粒子的个体适应度fh,更新(ph,fh),构造键值对(key,value)。
3)Reduce操作,获取每个群组最佳适应度和最优解,用公式(13)得出F,以ID为key,value的(F,(pb,fg))键值对,再Join操作,与步骤2)的键值对接,更新(F,(pb,fb)),若差分进化迭代结束,输出pb。
4)pb满足目标适应度E,停止差分进化迭代,输出最优pb,否,判断F是否满足,否,Map操作,用粒子群算法公式(8)~(9)获得x,v更新(x,v),同时以ID编号为key值,value(x,v)转至步骤2),F满足,转至e。
5)Map操作,以ZID为key,其他数据为value,重新构造键值对(key,value)。
6)再进行一次Reduce操作,以AID为key,(pfm/2,D+1)为value,选择较好m/2群组(phm/2,D+1)的最佳位置和最佳适应度,Join操作,与步骤5)的键值对连接。
7)进行一次Map操作,以ID为key,其他数据为value,用改进的差分进化算法,得出x和v,更新(x,v),转到步骤2)。
5 实验与分析
5.1 预测误差评估指标
为了对提出的算法有效地评估,选用均方根误差(RMSE)和平均绝对百分比误差(MAPE)作为光伏发电预测误差的指标。
MAPE评估系统的预测能力,RMSE评估预测值的离散程度[25-26]。公式分别如下:
(21)
(22)
式中,N为光伏发电功率输出个数;Pn,i为第i时间段实际的光伏输出功率;An,1是第i时间段预测的光伏输出功率。
5.2 预测模型验证
实验数据来源于本地30 kW分布式光伏电站2020年3月24到2021年12月31的光伏发电功率数据和气象信息,每组数据样本包含6:00~18:00的12个时间点云量信息、日最高温度、日最低温度、最高湿度以及最低湿度共16个环境输入变量,和6:00~18:00的12个时间点光伏输出功率共12个功率输出变量。
为了验证预测模型的有效性,选取晴转多云、阴转多云以及雨天的天气类型的待测日,采用本模型方法进行相似样本集筛选、训练、预测,用RMSE、MAPE进行分析,再通过BP、PSO-BP、PSO-DE-BP三种优化算法进行对比分析,包括预测精度以及稳定性分析。
表7~9分别选取2021年2月24日,天气类型为晴转多云;2021年6月20日,天气类型为阴转多云;以及2021年9月17日,天气类型为雷阵雨转阴作为待测日,采用本文提出的算法,以各个时间点云量作为输入变量,跟踪预测一天当中的天气类型变化。由表7~9可以得出,晴转多云天气预测精度高于阴转多云以及阵雨天气。
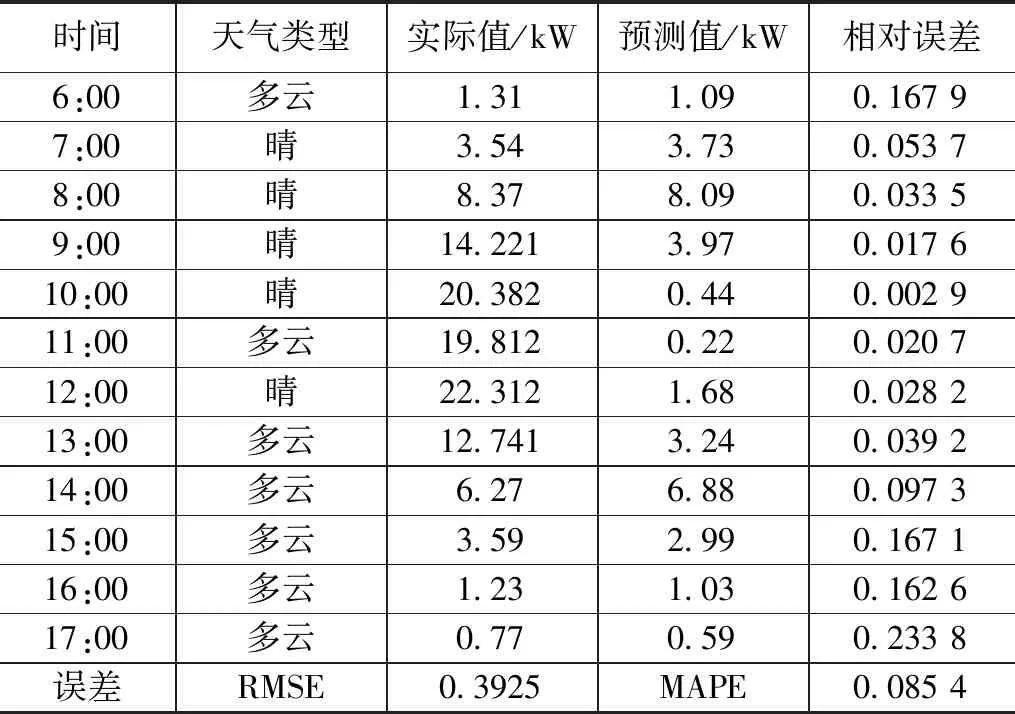
表7 预测日天气类型为晴转多云误差分析表
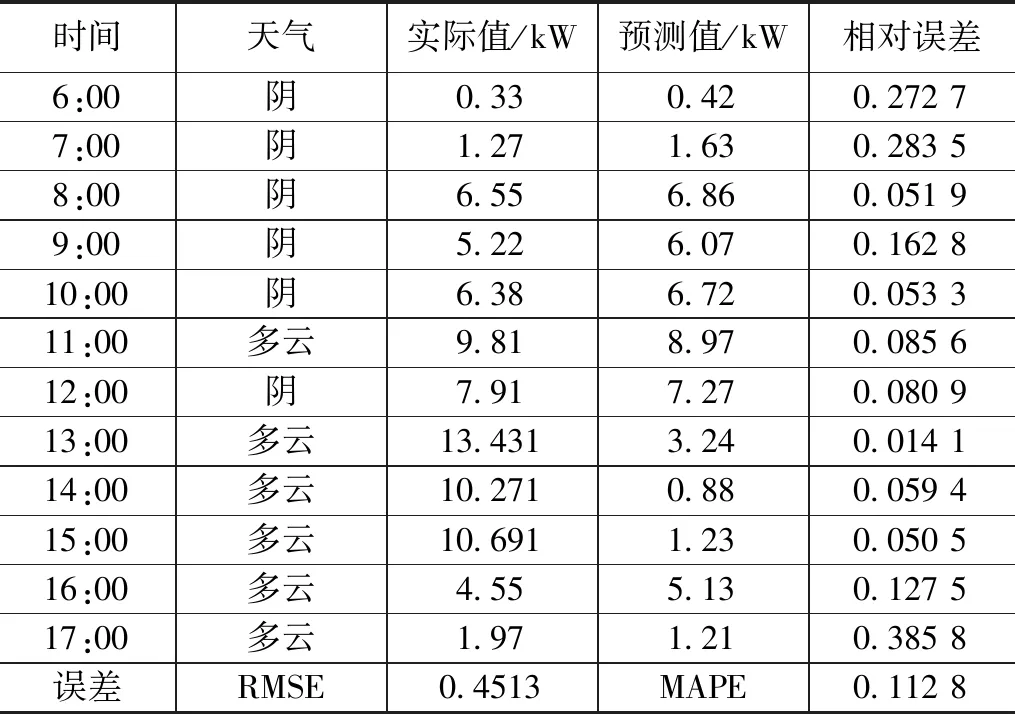
表8 预测日天气类型为阴转多云误差分析表
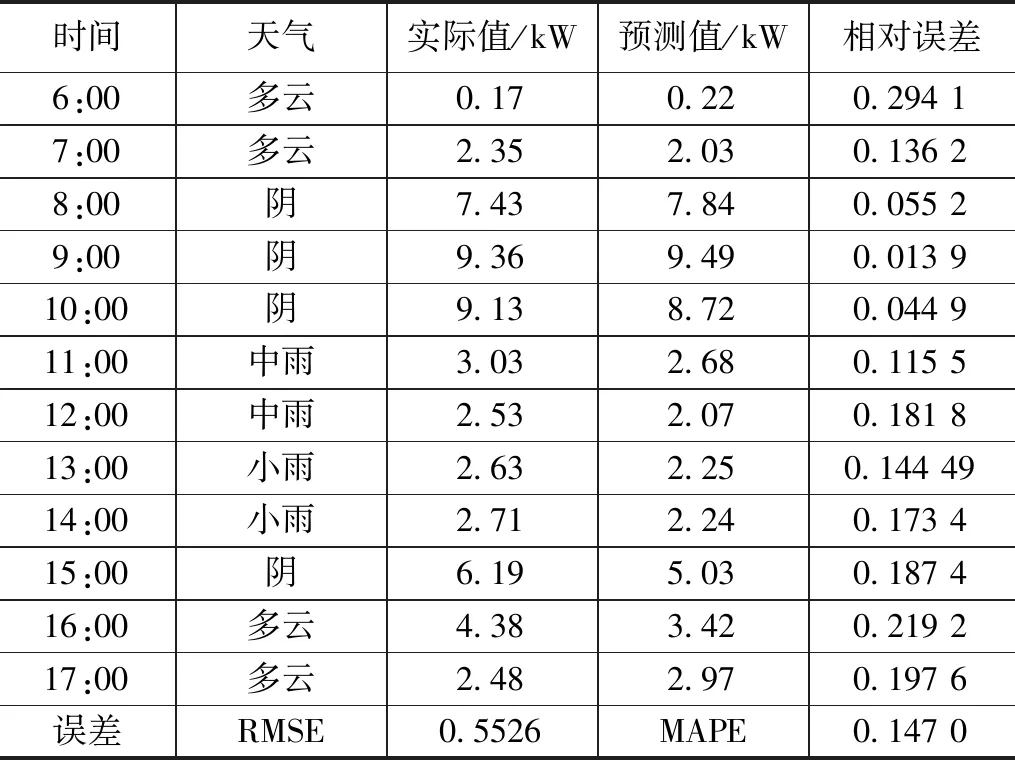
表9 预测日天气类型为雨天误差分析表
5.3 PSO-DE-BP算法性能分析
为了进一步明确算法在不同天气下功率预测的通用性,分别使用PSO-DE-BP、PSO-BP、BP三种算法对模型进行训练。对晴天、阴天以及雨天进行相似天气分组,求得每种天气状况下预测的平均误差,分别见表10~12。

表10 晴天预测误差分析表

表11 阴天预测误差分析表

表12 雨天预测误差分析表
由表10~12三种方法精度对比分析得出,晴天预测误差明显优于阴天和雨天,这是由于云量变化的随机性导致预测准确性降低。且PSO-DE-BP方法的误差要小于BP以及PSO-BP两种算法,因此采用该算法可获得更稳定的网络。
5.4 算法并行性能分析
为了测试PSO-DE-BP算法的并行化性能,采用加速比来测试算法的并行性能,加速比是衡量并行系统或程序并行化的性能和效果的指标[27],如公式(23)所示,其中Tsingle单机下运行的时间,Tparallel表示该算法并行化下运行的时间,Sspeed是衡量并行性能的指标,该值越大,算法的并行性能的效果越好。
Sspeed=Tsingle/Tparallel
(23)
通过增加集群的节点以及样本的数据量,来测试PSO-DE-BP算法的并行性能,表格13所示,单节点相当于单机运算。
表13可知,随着节点数的增长,加速比的增长率变缓。因为节点数越大,集群之间的通信和任务调度越多,消耗时间也增多。随着样本数据量的增加,加速比与节点数更接近同比例增长。因此,PSO-DE-BP算法能满足海量高维电力数据的负荷预测的性能要求。
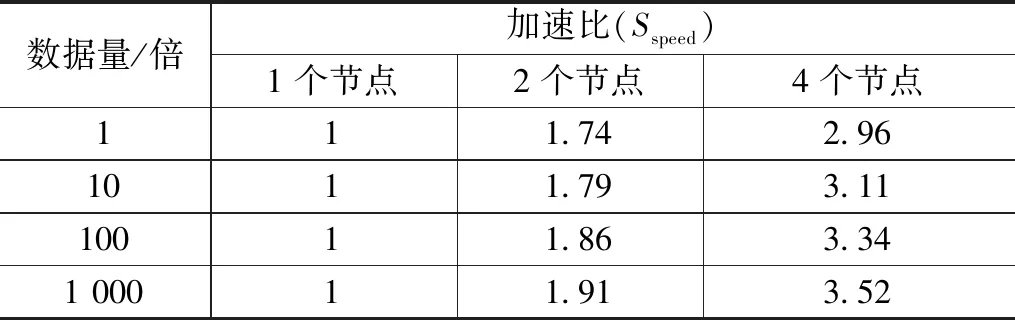
表13 加速比与群集节点及样本数量关系
6 结束语
本文首先建立了一个以各个时间段的云量作为输入变量的神经网络结构,用云量跟踪天气的变化情况,有效提高了多云、阴雨天的预测精度。然后基于PSO-DE-BP混合算法对BP神经网络初始值进行优化,通过粒子群分组优化,分别用PSO和改进的DE对群内、群间迭代进化,引进了种群多样性算法,避免早熟现象,寻找全局最优,与BP算法和PSO-BP相比,具有更高的稳定性和预测精度。
通过基于Spark的内存分布式计算思想,引进到PSO-DE-BP混合算法中,实行并行计算,通过加速比分析,PSO-DE-BP算法具有良好的并行性能和处理大规模数据的能力。

