双电机驱动的管道检测机器人空间定位

王鲁辉 李 巍 李生文 李太江 程晔锋 徐向前

（1. 西安石油大学材料科学与工程学院，陕西 西安 710000；2. 西安热工研究院有限公司，陕西 西安 710000）

0 引言

管道运输是石油和天然气等化工产品和原料的重要运输方式，近几十年发展迅速。截至2021年底，全球在役管道总里程约202万公里，随着人类对石油、天然气需求量不断增加，全球范围内管道铺设总里程仍将持续上升。同时，管道在夜以继日的运行消耗后，对维护人员来说检测工作是一项巨大的挑战[1-3]。

在早期的管道检测工作中，作业人员一般都采用整体挖掘法，将埋藏整条管道的土壤挖开检查。传统的检测手段，不仅检查效率低，还非常消耗人力、物力，检测的效果也不理想，很容易对运输管道造成伤害并延误管道的使用。因此，管道检测工程开始逐渐使用管道检测机器人来代替作业人员开展检测工作[4-6]。但是，对于管道检测机器人而言，准确的管内定位技术是其正常稳定工作的前提条件之一，本文将针对双电机驱动机器人在管道内的空间定位问题展开研究。

1 机器人电机的PID算法分析及仿真

1.1 PID算法分析

机器人电机驱动模块的选择至关重要，需要具有体积小、力矩大、噪音小等优点，同时还支持调速和正反转功能。本研究中机器人采用型号为TBSM52-20B33的伺服电机，具体性能参数如表1所示。

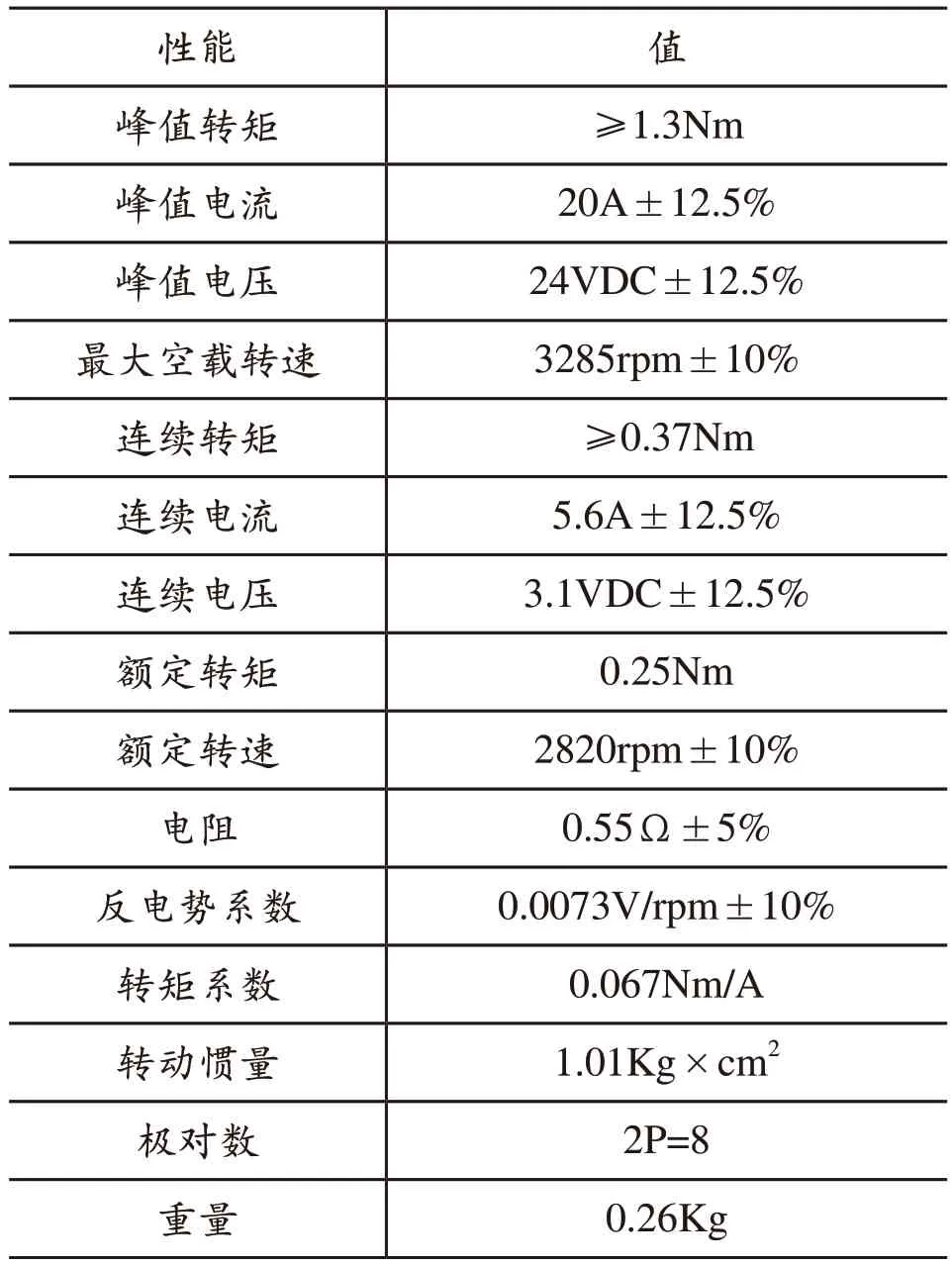
表1 TBSM52-20B33伺服电机性能参数

为了提高电机的抗干扰能力，选择串级PID控制器驱动控制电机工作，即速度环和电流环双闭环设计。其控制框图如图1所示，该算法不仅可以抑制速度环路中的干扰，还可以抑制电流通道的干扰。输入误差根据系统闭环环路的组成可以分为实际速度测量值和速度标称值之间的偏差，实际电流测量值和电流标称值之间的偏差[7-9]。

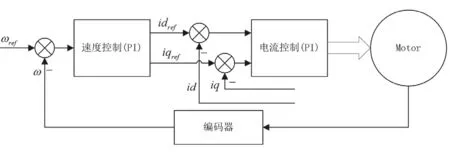
图1 电机串级PID控制结构

在时域上，PID控制算法可以描述为：

式中，Kp为比例常数，Ti为积分时间常数，Td为微分时间常数，均需要根据实际系统需要调节的参数，e（t）为误差信号。在频域上，对应的频域方程为：

在PID控制算法的三个部分中，比例项在系统暂态时其主要作用，增大比例系数能够提高响应速度，但同时也会导致系统超调，过大甚至会影响系统的稳定性，但单纯的比例控制出现静态误差。因此，需要引入积分项消除静态误差，积分项主要在系统进入稳态后其主要作用，通过不断累加误差来达到消除误差的目的，但是积分项的引入会使在控制初始阶段超调量增加，系统出现滞后。为了避免过大的超调需要适当减弱积分作用。所以积分系数的选择应综合考虑超调量和静态误差的大小。微分项主要用来提前修正误差，并能起到缩短调节时间和减小超调，同时也能够抵消积分引入带来的滞后问题，但是实际应用中一般不会加入微分项，因为通过差分的方式来等价微分的形式往往会放大系统中的干扰，影响系统的控制效果，所以速度环和电流环均采用的PI设计。

1.2 PID算法验证

以速度环的PI控制器为例，说明PI参数的不停对于速度环控制的影响。直观的表现就在于速度环的给定速度与经过PI控制器后的反馈速度的区别。

首先给定一组较好的参数作为示范Kp=2.3，Ki=38，分别对每个参数的影响进行仿真分析，同样都在0.3秒时给予一个突变的速度500rpm。转速的仿真结果如图2所示。

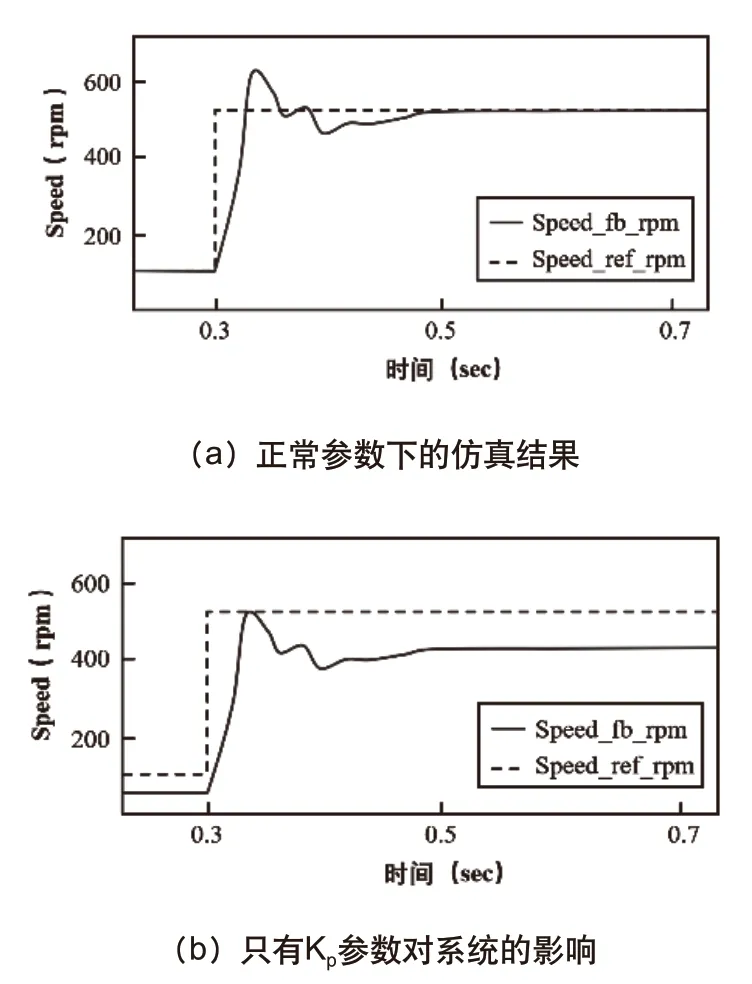
图2 Kp和Ki对控制系统的影响

比例控制是一种较为简单的控制方式。其控制器的输出与输入误差信号成比例关系。当仅有比例控制时系统输出存在稳态误差（b），明显的可以看出了Ki对于系统最直观的影响就是可以消减系统的稳态误差。在积分控制中，控制器的输出与输入误差信号的积分成正比关系。为了消除稳态误差，在控制器中必须引入“积分项”。积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。这样，即便误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大使稳态误差进一步减小，直到等于零。因此，比例+积分（PI）控制器，可以使系统在进入稳态后无稳态误差（a）。

进一步，测试PI调节参数对控制性能的影响，最终效果如图3所示。

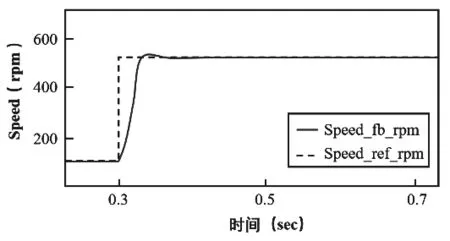
图3 PI参数对速度的影响

2 双电机驱动的管道检测机器人的定位研究

上述部分的测试，验证了PID算法可减小控制时间，减小了稳态误差，具备良好的速度控制性能。构建双电机驱动的机器人，机器人共有四个车轮，前边两个车轮为驱动轮，后边两个车轮为从动轮用于支撑机器人，利用PID算法控制两个驱动轮的速度，通过控制速度差实现机器人的左右转向和直线行驶。在此基础上，对双电机驱动的机器人进行定位研究。

机器人内安装有高精度编码器和陀螺仪，编码器用于测量速度和运行距离信息、陀螺仪用于获得方位角测量信息。采用相对定位方式，基于位移、位置、方位角以及数学中的坐标变换原理对双电机驱动的管道检测机器人进行高精度空间定位[10,11]。

机器人姿态信息由安装在机器人上的陀螺仪采集并送出，但由于机器人处于运动状态时，陀螺仪也随着机器人的运动而运动，从而使得由陀螺仪所确定的机器人自身坐标系不断地变化。而变化的坐标系不便于对机器人坐标的表示，因此在机器人初始位置所在的坐标位置建立世界坐标系，该世界坐标系与机器人初始位置的坐标系重合，如图4（a）所示，以垂直地面向上的方向为Z轴正方向，Y轴正方向为机器人此时的朝向，Y轴顺时针方向旋转九十度后与X轴重合。机器人运动后某一时刻世界坐标系与机器人自身坐标系的关系如图4（b）所示。

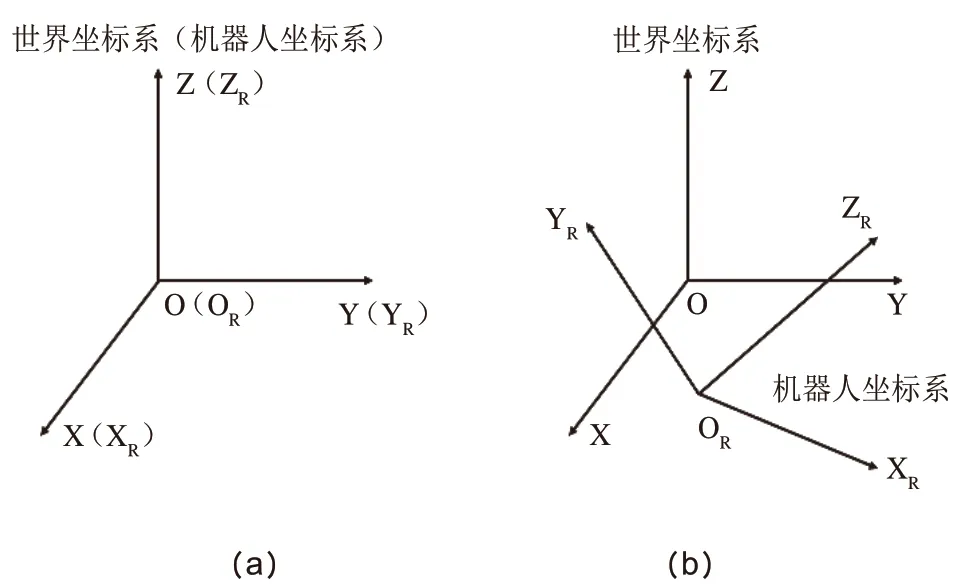
图4 坐标系关系

2.1 双电机驱动的机器人空间位移计算

现规定将机器人前两车轮的中点坐标位置视作机器人本身的坐标位置，位移大小L表示该中点的位移大小。以下将对机器人位移计算展开分析，本文中机器人的转向是利用左右两轮速度差完成的，机器人通过定义以下变量，辅助位移大小L的计算。

D：机器人两车轮间距；

L1：机器人左轮通过路程；

L2：机器人右轮通过路程；

θ：机器人转向时车轮走过的圆弧所对应的圆心角；

θ1、θ2：分别为机器人左右车轮转动的总角度；

R：机器人转向时左车轮路径所在圆的半径；

r：机器人车轮半径。

机器人的运动大致可分为三种情况：左右两车轮速度相同的直行、左右两车轮差速同向转动的转弯、左右两车轮转动方向相反的转弯。

（1）左右两车轮速度相同的直行

此时左右两车轮的移动距离即为机器人所移动的位移大小，前进或后退位移大小满足：

（2）左右两车轮差速同向转动的转弯

以机器人右轮转速大于左轮进行差速向左转向时为例，位移大小L如图5所示。

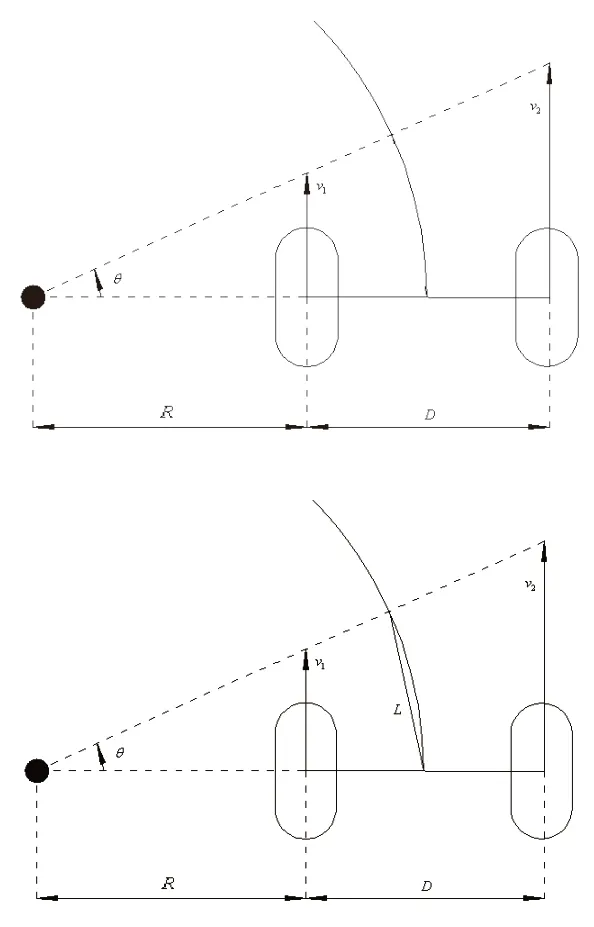
图5 机器人转弯原理图

由可知，机器人差速向左转向时位移大小L近似等于圆心角θ所对应的圆弧长度：

机器人实际运动时，陀螺仪和编码器采集数据的频率可达到50Hz，机器人转弯时，单位时间内机器人车轮走过的圆弧所对应的圆心角θ趋近于0，所以圆心角θ与其反正切值近似相等。可近似等价为机器人在单位时间内做了一次沿机器人前进方向的匀速直线运动，此时等价的位移大小L如图6所示。

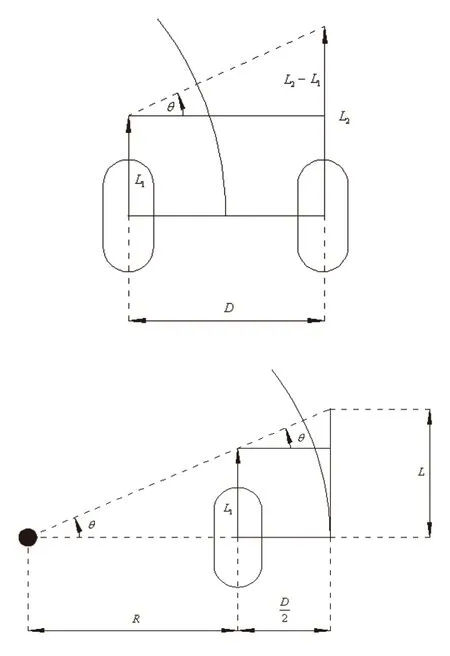
图6 圆心角的计算原理

由图3可以得到：

等价的位移大小L由计算：

考虑到机器人向不同方向转弯时，L1与L2的大小关系会发生变化，当机器人向左转向时L1L2。因此，当机器人进行左右两车轮同向差速转向时，位移大小L可由下式给出：

（3）左右两车轮转动方向相反的转弯

当机器人进行左右两车轮转动方向相反的转向时又包含两类情况，即：L1等于L2和L1不等于L2。

当左车轮后退右车轮前进且行进距离L1等于L2，机器人转动情况如图7所示。

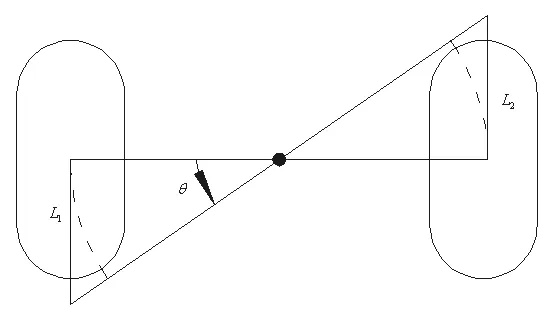
图7 两车轮反向转动情况

可以看出在此种状态下，机器人的中心位置没有发生移动。此时机器人位移大小为零：

机器人转过的圆心角：

当左车轮后退右车轮前进且行进距离L1不等于L2时机器人转动情况如图8所示。

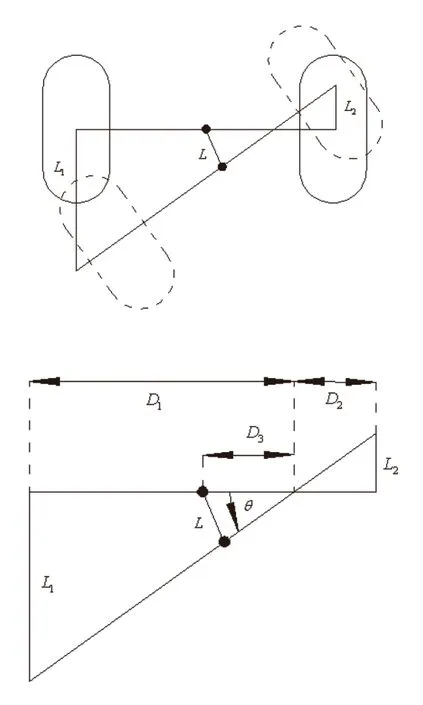
图8 两车轮反向转动且前进距离不同时的转动情况

此时圆心角和位移满足：

因此，当机器人进行左右两车轮转动方向相反的转向时的位移大小如下：

2.2 双电机驱动的机器人空间位置计算

由于机器人的速度、加速度、位移等的表示均是基于机器人坐标系，不能直接与世界坐标系内的变量进行运算。选取的陀螺仪恰好能够给出机器人坐标系相对于世界坐标系三个坐标轴方向的旋转量，根据该旋转量由旋转矩阵对机器人坐标系内的向量进行处理即可实现对机器人坐标系内的向量在世界坐标系内的投影显示。

同样规定将机器人前两车轮的中点坐标位置视作机器人本身的坐标位置，以下说明通过旋转矩阵怎样实现位置的计算。由陀螺仪采集对应X、Y、Z坐标轴方向的旋转角度量，分别为α，β，γ。

坐标系单独绕X，Y，Z轴旋转的旋转矩阵如下：

由欧拉角表示姿态时坐标系旋转顺序定义为Z-Y-X，将总的旋转矩阵记为R=Rz×Ry×Rx，旋转矩阵可反映出机器人的姿态变化。

同时，通过计算可以由偏转角度量α，β，γ得到机器人单位时间内的位移大小在世界坐标系三个坐标轴方向上的比重xi、yi、zi满足：

对上述三个坐标轴方向上比重进行单位化处理得Xi、Yi、Zi，可得：

位移大小对于坐标的确定也有着影响，记一时间段内机器人通过的位移大小为L,机器人在该时间段内的位移大小在三个坐标轴方向上的分量△X、△Y、△Z由计算可得：

结合上式，通过坐标的累加，可得到机器人当前坐标（Xt+1，Yt+1，Zt+1），计算如下：

2.3 双电机驱动的管道检测机器人的定位算法验证

为了验证以上定位算法的可行性，控制机器人分别在平面上直线运动、圆周运动以及在管道外部沿管壁圆周运动，规定机器人左右两轮连线的中点位置视为机器人所在位置。

首先，分别对机器人三种远动过程，采集30组实际轨迹点，通过Origin软件对实际运动轨迹进行了仿真处理，如图9～图11中的实际值所示。

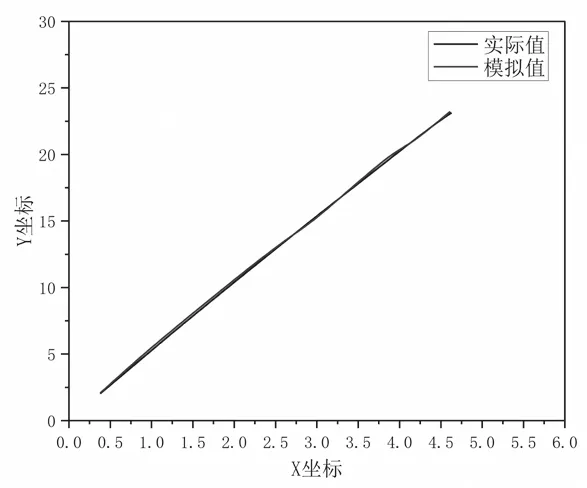
图9 直线运动仿真轨迹

图10 圆周运动仿真轨迹

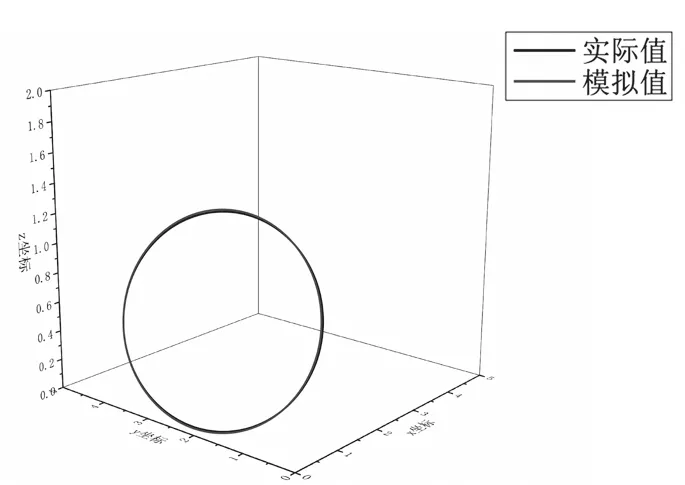
图11 管壁外圆周运动仿真轨迹

其次，通过双电机驱动管道检测机器人定位算法，分别对运动过程的位置坐标进行计算，取30组位置坐标，通过Origin软件对运动轨迹进行了模拟仿真，如图9～图11中的模拟值所示。

以下三图给出了机器人实际运动轨迹（实际值）与基于双电机驱动机器人定位算法所得运动轨迹（模拟值）的仿真结果对比。

观察图中轨迹可得，两个轨迹基本重叠；后对每组实际轨迹与算法计算所得轨迹的30组位置坐标进行了误差计算，求得平均误差小于3.5%，属于合理误差范围内。因此，验证了该算法应用于双电机驱动机器人空间定位具有较好的可靠性。

3 结语

（1）构建双电机驱动的机器人模型，通过PID算法能够有效控制机器人驱动轮的差速运转，实现机器人左右转向和直线运动；

（2）基于所推空间位置算法，开展双电机驱动机器人管道定位试验。控制检测机器人在平面上直线运动、圆周运动以及在管道外部沿管壁圆周运动，对比定位算法所得仿真轨迹与实际运动仿真轨迹，并进行了误差分析。最终验证了该定位算法应用于双驱机器人管道空间定位时的可靠性。