一类双元型不等式成立求参问题解法探究
2023-06-01 10:11贵州省铜仁第一中学554300
中学数学研究(江西) 2023年6期
贵州省铜仁第一中学 (554300) 王 钰
在一些含有存在量词或全称量词的导数综合问题中,会出现含有两个变元x1,x2的不等式恒成立或有条件成立求其中参数范围问题,由于各类题中所给的数学用语的不同,这些问题也就体现出不同的数学函义,常见类型的问题经过等价转化后,可变形为下列不同情形的关于两个函数最值的不等式问题.本文并通过几个典型例题的分析点评,对此进行分类归纳,以探求常见题型解题思路,仅供读者参考.
一、对于∀x1∈D,∀x2∈E,都有f(x1)
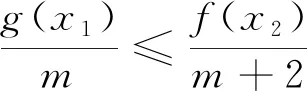
点评:在转化了由两个量词表述的不等式后,则题目就转变成了如何求两个函数的最大值与最小值的问题了,这里的转化是解题关键,必须要正确无误.
二、对于∀x1∈D,∀x2∈E,都有f(x1)>g(x2)恒成立,则f(x)min>g(x)max
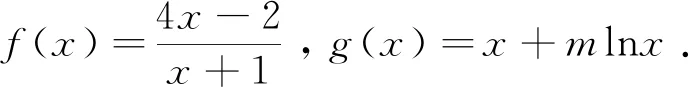
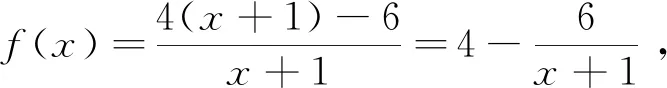
点评:本解法通过将问题转化变成一个恒不等式,然后再进行分离参数处理,转化为求另外一个新函数的求最值问题,这是对一些复杂问题所采取的分层处理的重要措施.
三、对于∀x1∈D,∃x2∈E,使f(x1)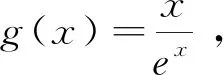
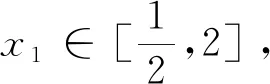
点评:在本题中出现的是先任意,后存在的两种量词,由于用“≤”连接,则可转化两个最大值的不等关系,然后求出两个函数最大值就是求解的重要部分了.
四、对于∀x1∈D,∃x2∈E,使f(x1)>g(x2)成立,则f(x)min>g(x)min.
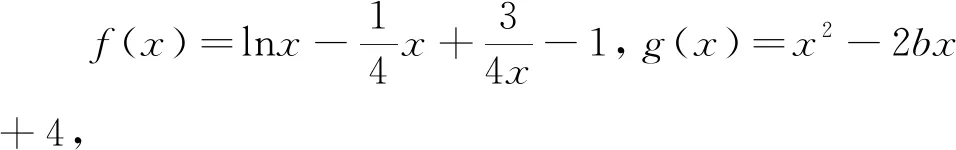
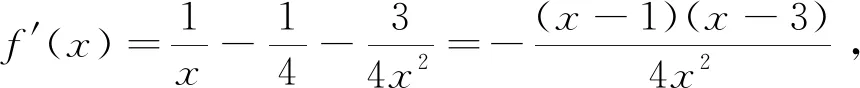
点评:本题与例3的条件类似,只是给出的不等式是用“≥”连接,但是对应数学意义也是不同的,此处是转化为求两个函数最小值问题,必须注意正确区分.
五、若∃x1∈D,∃x2∈E,使f(x1)>g(x2)成立,则f(x)max>g(x)min

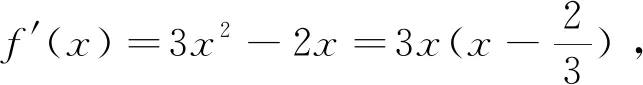
点评:在将题目转化两个函数的最大值与最小值问题后,再根据后面解题的需要,还需进一步转化,即经过分离变量后转化为一个新的不等式恒成立问题.
六、若∃x1∈D,∃x2∈E,使f(x1)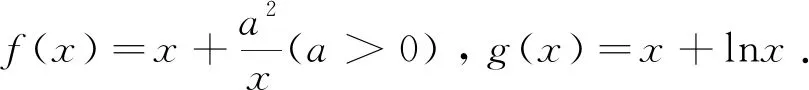
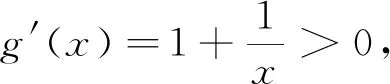
点评:在解题过程中,由于不能通过分离参数法解决问题,就采用了分类讨论的方法,通过比较a在区间[1,e]上的位置,确定分段标准,分析讨论后才能确认答案.
以上举例介绍了双元型不等式六类求参数范围问题的转化求解方法,这六类情形容易搞混,必须认识清楚、理解到位.关于双元型不等式成立求参数问题的求解方法是:遵循双元化一元,逐一处理的策略,运用分离参数、分类讨论的办法.
猜你喜欢
单调任意恒成立,论参离参定最值中学生数理化(高中版.高二数学)(2022年3期)2022-04-26 聚焦圆锥曲线中的最值问题中学生数理化(高中版.高考数学)(2021年12期)2021-03-08 巧用不等式求最值河北理科教学研究(2020年3期)2021-01-04 集合、充要条件、量词新世纪智能(数学备考)(2020年9期)2021-01-04 十二生肖议量词小天使·一年级语数英综合(2020年3期)2020-12-16 数列中的最值题型例讲中学生数理化(高中版.高二数学)(2020年11期)2020-12-15 量词大集合学生天地(2020年24期)2020-06-09 精选课本题改编练习新高考·高二数学(2017年9期)2018-03-16 摆放套娃幼儿智力世界(2016年1期)2016-05-30 量词歌小学阅读指南·低年级版(2016年3期)2016-05-27

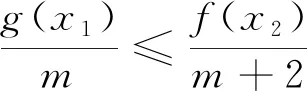
点评:在转化了由两个量词表述的不等式后,则题目就转变成了如何求两个函数的最大值与最小值的问题了,这里的转化是解题关键,必须要正确无误.
二、对于∀x1∈D,∀x2∈E,都有f(x1)>g(x2)恒成立,则f(x)min>g(x)max
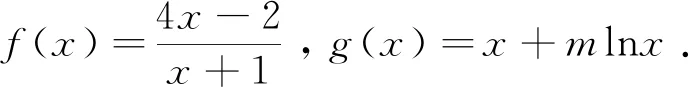
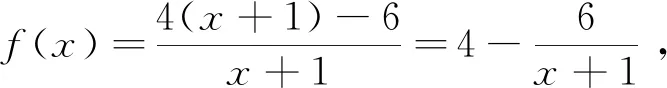
点评:本解法通过将问题转化变成一个恒不等式,然后再进行分离参数处理,转化为求另外一个新函数的求最值问题,这是对一些复杂问题所采取的分层处理的重要措施.
三、对于∀x1∈D,∃x2∈E,使f(x1)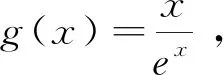
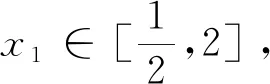
点评:在本题中出现的是先任意,后存在的两种量词,由于用“≤”连接,则可转化两个最大值的不等关系,然后求出两个函数最大值就是求解的重要部分了.
四、对于∀x1∈D,∃x2∈E,使f(x1)>g(x2)成立,则f(x)min>g(x)min.
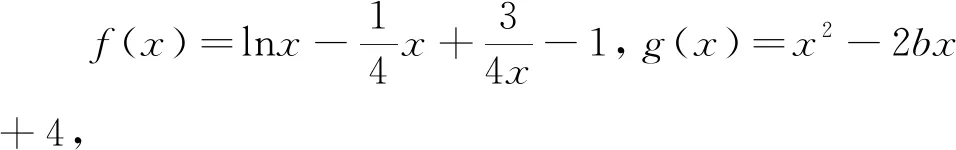
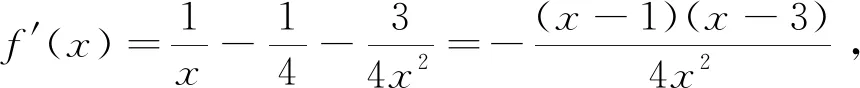
点评:本题与例3的条件类似,只是给出的不等式是用“≥”连接,但是对应数学意义也是不同的,此处是转化为求两个函数最小值问题,必须注意正确区分.
五、若∃x1∈D,∃x2∈E,使f(x1)>g(x2)成立,则f(x)max>g(x)min

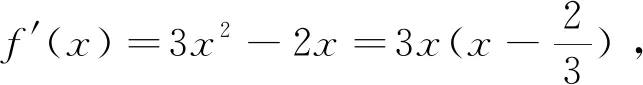
点评:在将题目转化两个函数的最大值与最小值问题后,再根据后面解题的需要,还需进一步转化,即经过分离变量后转化为一个新的不等式恒成立问题.
六、若∃x1∈D,∃x2∈E,使f(x1)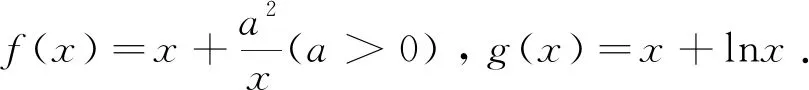
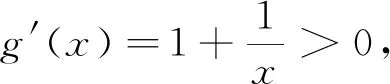
点评:在解题过程中,由于不能通过分离参数法解决问题,就采用了分类讨论的方法,通过比较a在区间[1,e]上的位置,确定分段标准,分析讨论后才能确认答案.
以上举例介绍了双元型不等式六类求参数范围问题的转化求解方法,这六类情形容易搞混,必须认识清楚、理解到位.关于双元型不等式成立求参数问题的求解方法是:遵循双元化一元,逐一处理的策略,运用分离参数、分类讨论的办法.
猜你喜欢
单调任意恒成立,论参离参定最值中学生数理化(高中版.高二数学)(2022年3期)2022-04-26 聚焦圆锥曲线中的最值问题中学生数理化(高中版.高考数学)(2021年12期)2021-03-08 巧用不等式求最值河北理科教学研究(2020年3期)2021-01-04 集合、充要条件、量词新世纪智能(数学备考)(2020年9期)2021-01-04 十二生肖议量词小天使·一年级语数英综合(2020年3期)2020-12-16 数列中的最值题型例讲中学生数理化(高中版.高二数学)(2020年11期)2020-12-15 量词大集合学生天地(2020年24期)2020-06-09 精选课本题改编练习新高考·高二数学(2017年9期)2018-03-16 摆放套娃幼儿智力世界(2016年1期)2016-05-30 量词歌小学阅读指南·低年级版(2016年3期)2016-05-27
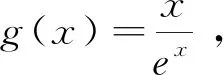
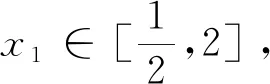
点评:在本题中出现的是先任意,后存在的两种量词,由于用“≤”连接,则可转化两个最大值的不等关系,然后求出两个函数最大值就是求解的重要部分了.
四、对于∀x1∈D,∃x2∈E,使f(x1)>g(x2)成立,则f(x)min>g(x)min.
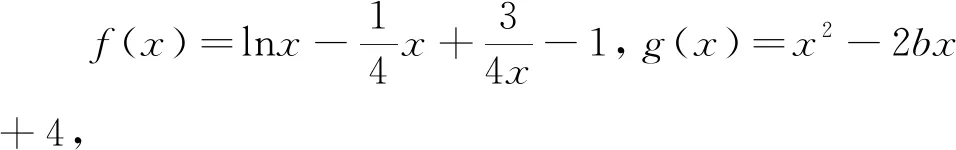
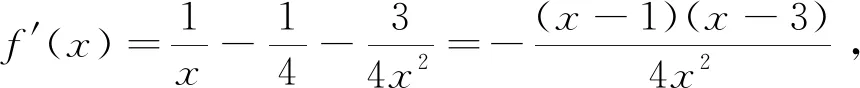
点评:本题与例3的条件类似,只是给出的不等式是用“≥”连接,但是对应数学意义也是不同的,此处是转化为求两个函数最小值问题,必须注意正确区分.
五、若∃x1∈D,∃x2∈E,使f(x1)>g(x2)成立,则f(x)max>g(x)min

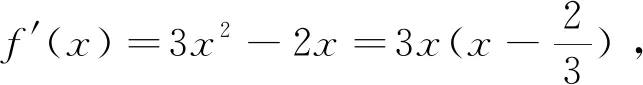
点评:在将题目转化两个函数的最大值与最小值问题后,再根据后面解题的需要,还需进一步转化,即经过分离变量后转化为一个新的不等式恒成立问题.
六、若∃x1∈D,∃x2∈E,使f(x1)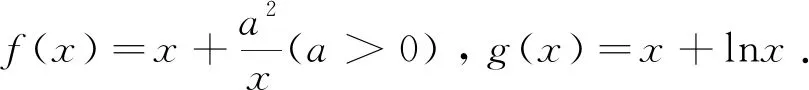
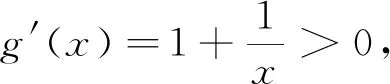
点评:在解题过程中,由于不能通过分离参数法解决问题,就采用了分类讨论的方法,通过比较a在区间[1,e]上的位置,确定分段标准,分析讨论后才能确认答案.
以上举例介绍了双元型不等式六类求参数范围问题的转化求解方法,这六类情形容易搞混,必须认识清楚、理解到位.关于双元型不等式成立求参数问题的求解方法是:遵循双元化一元,逐一处理的策略,运用分离参数、分类讨论的办法.
猜你喜欢
单调任意恒成立,论参离参定最值中学生数理化(高中版.高二数学)(2022年3期)2022-04-26 聚焦圆锥曲线中的最值问题中学生数理化(高中版.高考数学)(2021年12期)2021-03-08 巧用不等式求最值河北理科教学研究(2020年3期)2021-01-04 集合、充要条件、量词新世纪智能(数学备考)(2020年9期)2021-01-04 十二生肖议量词小天使·一年级语数英综合(2020年3期)2020-12-16 数列中的最值题型例讲中学生数理化(高中版.高二数学)(2020年11期)2020-12-15 量词大集合学生天地(2020年24期)2020-06-09 精选课本题改编练习新高考·高二数学(2017年9期)2018-03-16 摆放套娃幼儿智力世界(2016年1期)2016-05-30 量词歌小学阅读指南·低年级版(2016年3期)2016-05-27
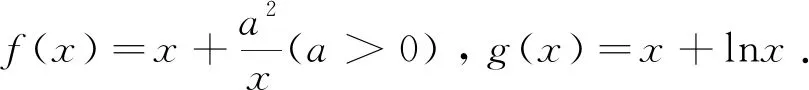
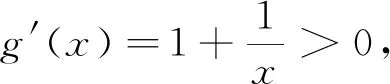
点评:在解题过程中,由于不能通过分离参数法解决问题,就采用了分类讨论的方法,通过比较a在区间[1,e]上的位置,确定分段标准,分析讨论后才能确认答案.
以上举例介绍了双元型不等式六类求参数范围问题的转化求解方法,这六类情形容易搞混,必须认识清楚、理解到位.关于双元型不等式成立求参数问题的求解方法是:遵循双元化一元,逐一处理的策略,运用分离参数、分类讨论的办法.
猜你喜欢
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
河北理科教学研究(2020年3期)2021-01-04
新世纪智能(数学备考)(2020年9期)2021-01-04
小天使·一年级语数英综合(2020年3期)2020-12-16
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
学生天地(2020年24期)2020-06-09
新高考·高二数学(2017年9期)2018-03-16
幼儿智力世界(2016年1期)2016-05-30
小学阅读指南·低年级版(2016年3期)2016-05-27

