解决“指对同构“问题的一种简单方法

江苏省扬州市第一中学 (225000) 周定祥

利用同构法来解决函数恒成立问题是近几年高考的热点,而“同构”法中又以“指对同构”最为复杂,其隐藏深,构造方法巧妙会使大部分同学望而生畏.本文以2020届新高考一卷第21题与江西八校2022届4月联考第12题为例来谈谈我的解法.

例1 (2020新高考一卷第21题)已知函数f(x)=aex-1-lnx+lna(2)若f(x)≥1,求a的取值范围.

解法一:∵aex-1-lnx+lna≥1,∴elnaex-1-lnx+lna≥1,∴elna+x-1-lnx+lna≥1,∴elna+x-1+lna-1≥lnx,∴elna+x-1+lna+x-1≥lnx+x,∴elna+x-1+lna+x-1≥elnx+lnx.

令g(x)=ex+x,即g(lna+x-1)≥g(lnx).下面讨论g(x)单调性即可,过程略.

解法二:∵aex-1-lnx+lna≥1,∴aex-1+lna-1+x≥lnx+x,∴aex-1+lna+lnex-1≥lnx+x,∴aex-1+ln(aex-1)≥lnx+x,令g(x)=lnx+x,即g(aex-1)≥g(x),下面讨论g(x)单调性即可,过程略.

观察上面两种方法的同构过程,需要学生具有较强的观察能力和构造能力.一般采用法一的较多,法二更加不自然,对学生要求更高,那么有没有简化的方法?通过观察法一的过程,发现最后转化为讨论g(x)=ex+x的单调性,也就是把原不等式中对数形式转化成了指数形式.那可不可以开始就把对数式看成一个整体?

解法三:令t=lnx,则et=x①,原不等式转化为t≤elna+x-1+lna-1②,两式相加得et+t≤elna+x-1+lna+x-1,令g(x)=ex+x,得g(t)≤g(lna+x-1),即g(lna+x-1)≥g(lnx),下面讨论g(x)单调性即可,过程略.

同理,观察解法二的过程,发现最后转化为讨论g(x)=lnx+x单调性,也就是把原不等式中指数形式转化成了对数形式,那可不可以开始就把指数式看成整体?

解法四:令t=aex-1,∵a>0,∴aex-1>0,∴lnt=lna+x-1①,原不等式转化为t≥lnx-lna+1②,①②相加得lnt+t≥lnx+x.令g(x)=lnx+x,得g(t)≥g(x),即g(aex-1)≥g(x),下面讨论g(x)单调性即可.

解法四摒弃了传统“同构法“中的各种技巧,转化为观察等式与不等式的结构,通过加法得到”同构体“.降低学生上手的难度,当然最基本的同构知识还是要有比如:x=lnex=elnx.此方法有几个注意点,首先,不等式即②式需要把t放到不等式一侧,其余各式转移到另一侧,方便观察,其次,观察换元后的等式与原不等式之间的关系,可以相加也可以在保证同号的情况相乘.最后,如果相加或相乘后不能发现同构体,可以适当化简.

例2 (江西八校2022届4月联考第12题)已知函数f(x)=log3(3x+1)+mx(m∈R)是偶函数,函数g(x)=2e(k-1)x-3lnx+(3k-5)x,若g(x)≥2m+1恒成立,则实数k的取值范围为( ).

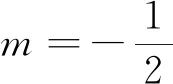
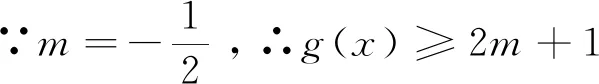
说明:法一为指数式转化为对数式,也可以对数式转化为指数式.