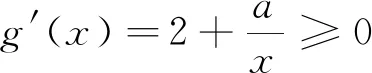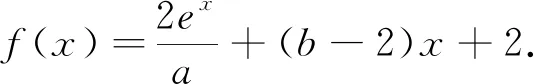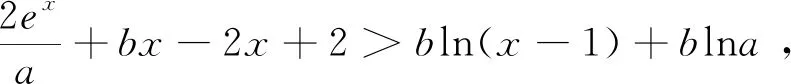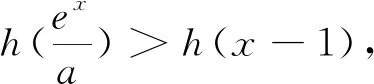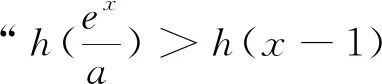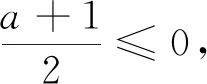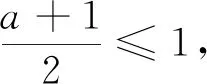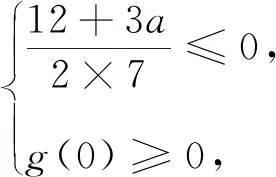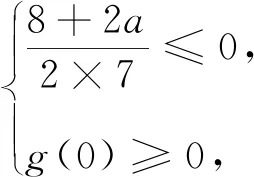为何错解如此流行——老调重弹函数的单调性

厦门大学附属实验中学 (363123) 田富德

不等式恒成立问题一直是高考、各类省市质检的热点.解决此类问题,最终均转化函数的最值问题,而函数导数是求解函数最值的重要方法.为了增加试题灵活性和简洁性,ex与lnx备受命题者的青睐.近几年,ex与lnx同时出现的题也如雨后春笋,直接构造函数求解往往比较复杂甚至不可解,利用同构策略结合函数的单调性大大减少了运算量,这也让广大师生把同构研究得更透彻.

1 同构思想的含义

导数问题中经常出现含参等式或不等式,很大一部分题是命题者利用函数单调性构造出来的,如果我们能找到这个函数模型,无疑大大加快解决问题的速度．即通过变形,使式子左右两边结构形式完全相同,找到不等式两边对应的同一函数模型,这就是同构法．例如:若F(x)≥0能等价变形为f[g(x)]≥f[h(x)],然后利用f(x)的单调性,如递增,则转化为g(x)≥h(x),简化式子,事半功倍．同构思想的本质是借助于函数的单调性性质对条件进行等价变换.

二、同构思想解题

例1 (2020山东高考)已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1,求a的取值范围.

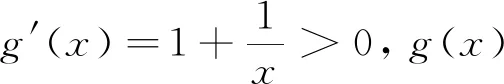
综上,a≥1.

点评:显然原不等式可化为aex-1-1+lna≥lnx,属于指对数混合型不等式恒成立问题,显然参数a是不可分离的,只能选择直接构造函数求导,此时往往导数较为复杂,上述解法利用函数单调性性质将原不等式等价转换为aex-1≥x,显然大大化简了原不等式,接下来解题就势如破竹了,这也是同构解题策略受广大师生青睐的原因.

三、为何错解如此流行

笔者刚好带了一届高三,各地质检卷做了不少,发现网上提供的解答、学生的答卷上、甚至部分老师提供的解答都清一色的犯了一个共同的错误——忽略了单调性变量取值的任意性,违背了“定义中的x1,x2均为区间内的两个任意取值,取值彼此互不依赖、互不影响.”错用单调性的定义进行解题.又由于错解所得到的结果与正解的结果一致,故得到错解的人还会以为自己获得了妙解.

1.错解展示

单调性经典错误性质:∀x∈E,当g(x)、h(x)∈D且g(x)f(h(x)),则函数f(x)在区间D上单调递减.

说明:本文约定,对于不等式f(g(x))

错因分析:虽然错误性质的变量x具有任意性,但对f(x)来说,内层函数变量的两个取值g(x)、h(x)并不具有任意性,呈相互影响、相互约制关系,违背了单调性定义的变量取值任意性,因此,错误性质条件下,得不到f(x)的单调性.

正确性质:“∀x∈E,当g(x)、h(x)∈D且g(x)f(h(x))”是“函数f(x)在区间D上单调递减”的必要不充分条件.

本文展示笔者所在省份的3道题的错误解法.

例2 (2022年漳州3月质检)已知f(x)=x2-x-alnx.

(1)若a=1,求f(x)的最小值;

(2)当x≥1时,f(2x-1)-2f(x)≥0,求a的取值范围.

错因分析:注意到上述解题过程中由“g(x2)≥g(2x-1)及x2≥2x-1”得到“g(x)在区间[1,+∞)单调递增”,解题者忽略了x2与2x-1并不任意取值,当其一确定,另一个变量的取值也随之确定.

例3 (2022年泉州1月质检)已知函数f(x)=ax-ex,∀x∈(1,+∞),f(x)

A．(-∞,1)B．(-∞,1]

C．(-∞,e)D．(-∞,e]

错解:因为alnx+a-ex=a(lnx+1)-elnx+1,所以∀x∈(1,+∞),f(x)f(x)在(1,+∞)恒成立,因为1

错因分析:注意到上述解题中由“f(lnx+1)>f(x)及1

(1)当a=2时,f(x)≥3恒成立,求b的值;

(2)当02时,f(x)>bln[a(x-1)]恒成立,求b的取值范围.

2.反例展示

例5 已知函数f(x)=(x-1)(x-a),∀x∈[0,+∞),f(2x)≥f(x)恒成立,求a的取值范围.

正解:依题意有(2x-1)(2x-a)≥(x-1)(x-a)在x∈[0,+∞)时恒成立,即3x2-x≥ax在x∈[0,+∞)时恒成立,即a≤(3x-1)min,x∈[0,+∞),从而有a≤-1.

流行原因分析:错解能得以流行的重要原因,其一,错解所得结果与正解所得结果一致,才有机会让大家认可错解,忽略错因;其二,正解过程可能繁杂,或是遇繁而退或是遇难而另辟蹊径,不小心误入错解.如例5所示,两种结果一致,如例2、例3及例4所示,大家可以网上查阅正确解法,皆比错解相对繁杂.

那么问题来了,我们总是可以利用错解得到答案,是不是对任何试题错解都能得到正确结果呢?答案显然是否定的.我们看如下反例:

例6 已知函数f(x)=(x-1)(x-a),∀x∈[1,+∞),f(2x)≥f(x)恒成立,求a的取值范围.

正解:依题意有(2x-1)(2x-a)≥(x-1)(x-a)在x∈[1,+∞)时恒成立,即3x2-x≥ax在x∈[1,+∞)时恒成立,即a≤(3x-1)min,x∈[1,+∞),从而有a≤2.

在例6中,显然错解得不到与正确一样的结果,那又为什么错解在众多试题屡屡成功骗到结果呢?对比例6与例2、例3、例4及例5的区别,可以发现例6在变量x起点处x=1时,内层变量不相等“2x≠x”,在例5中变量起点处x=0时,内层变量相等,即“2x=x”,这在例2、例3及例4也满足了类似的条件.

为什么众多试题均不更换区间起点来避开上述类似条件?笔者也尝试考试过更换例2、例3及例4的恒成立区间,都发现要么过程繁杂或几乎不可解,大家可以尝试看看,显然恒成立区间起点处内层变量相等受命题者的青睐.

在恒成立区间起点处内层函数变量相等的前提下,对于错误性质是不是就成立了呢?答案也是否定的.我们再看如下反例:

例7 已知函数f(x)=(x-2)2(x-a),∀x∈[0,+∞),有f(2x)≥f(x)恒成立,求a的取值范围.

在例7中,满足了变量起点处x=0时,内层变量相等,即“2x=x”,但利用错误性质仍不能得到正确结果.对比例7与前述例题,重大区别是,在参数变化中,例7的函数可能有3个单调区间,而例1至例6的函数均至多两个单调区间,尽管有的函数求导复杂,但单调区间并不多.在例1至例5中,恒成立区间起点处内层变量相等保证了在起点处附近函数只能单调递增,这样排除了先减后增的情况,先增后减又显然违备条件,因此在同构时,内层函数至多两个单调区间且区间起点处内层变量相等,错解可以得到正确的结果.但当内层函数可能3个或更多个区间时,错解就几乎不可能得到正确的结果了.

解题研究是中学数学一线教师及教研人员必做的功课,只能深刻理解试题背景蕴含的本质,才能站在至高点上引导学生解题,函数题海博大精深,本文旨在抛砖引玉,让更多的老师把此类问题研究的更加透彻,相互学习.