基于一道教材例题为背景的命题实践与思考

新疆教育科学研究院 (830049) 晏 鸿

在人教A版高中选择性必修第二册第5页例2的第(2)小问中有这样一道题:根据数列{an}的前4项2,0,2,0,…,写出数列的一个通项公式.题不难,但很典型,教材编者希望通过这道题回归数学概念本质,强化对“数列”和“通项公式”定义的理解,就看能不能挖掘它的深层价值,这也是命题的切入点.笔者进行了尝试,期待抛砖引玉.

一、命题历程

思路一 命制合格性学业水平考试难度试题

例1已知数列{an}前4项为3,1,3,1,…,则an=.(写出符合要求的一个答案即可).

立意分析:合格性学业水平考试是高中学生毕业或同等学力认定的依据,试题难度都不大,绝大多数都属于模仿改编题.对于教材上的例题,很容易得到一个通项公式an=(-1)n+1+1.在命题时,可以在这道例题上进行各种变式,如在这个数列各项上进行简单加1,就得到了本题的一个通项公式an=(-1)n+1+2.

在试题评析的过程中,还可以再进行追问和引导,让学生发现这个数列有两个特点:一是所有的奇数项和所有的偶数项都相同;二是每两个数字一循环.于是就产生了两个探究的方向,即分类讨论的方向与周期性方向.由于数列是特殊的函数,这两个方向实际上都是研究数列问题时常用的思维视角,同时也得到另外两个通项公式.

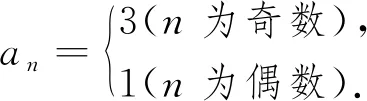
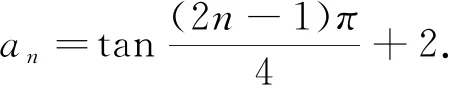
思路二 命制高考难度试题

例2 已知数列{an}前6项为2,-2,-2,2,-2,-2,…,则an=.(写出符合要求的一个答案即可).

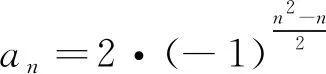
思路三 命制竞赛难度试题

例3已知数列{an}的前9项为1,1,1,2,2,2,3,3,3,…,则an=.(写出符合要求的一个答案即可).

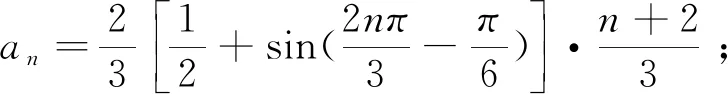
下面这几道类似题,供读者赏析.

①、已知数列{an}的前几项为0,1,0,2,0,3,…,则an=;

②、已知数列{an}的前几项为1,1,2,2,3,3,…,则an=;

③、已知数列{an}的前几项为2,0,0,2,0,0,2,0,0,…,则an=.

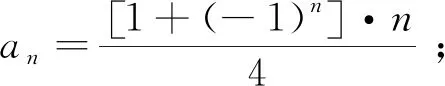
二、命题思考

基于以上的命题实践,提炼出如下命题原则和程序.

1.命制的试题要符合科学性、规范性的原则.试题内容与答案要科学合理,表述准确简洁,没有歧义,评分标准具有可操作性.灵活运用符号、图表、文字三种语言,使得字符图表匹配,图形规范优美,语言通俗易懂,能缓解学生解题压力,带给学生信心和动力.

2.命制的试题要有精准度和有效性.精准度是指试题的考查内容、考查的思想方法、检测的能力意识要有针对性.一般情况下,选择题、填空题每题考查知识点1～3个;解答题考查知识点3～6个、思想方法2～4个、能力意识2～3个.试题的思维量、运算量、阅读量及解答书写量都要恰当.有效性是指试题具有较好的检测功能,真正起到诊断问题、选拔分层的作用,如试题的内容、难度、信度、区分度跟题型、所处试卷的位置是否匹配,考查知识点之间搭配是否自然合理.

3.命制的试题要有思想性和公平性.试题要体现新课程的理念,对关键能力的考查要求.既要关注经济社会与科学技术的发展,突显素养立意,又要对城乡不同地域、不同生活经验的学生公平合理．

4.命制试题的基本程序.应包括立意与选材,关联与建构,加工与调整,审核与定型四个步骤,以此确保编题质量.