多孔介质中Brinkman方程组解的连续依赖性*

石金诚

广州华商学院数据科学学院，广东 广州 511300

Straughan et al.（1999）引入了具有Soret 效应且不可压缩的对流扩散Brinkman 方程，他们在有界区域内建立了解对Soret 系数的连续依赖性，有关Brinkman 方程更系统的介绍见文献（Nield et al.，1992；Straughan，2008）。偏微分方程（组）的连续依赖性或收敛性，称之为结构稳定性，关于结构稳定性的本质见文献（Ames et al.，1997）。

近年来，多孔介质中流体方程组的研究越来越受到学者们的关注，其中较为典型的流体方程组有Brinkman、Darcy 和Forchheimer 方程组，文献（Payne et al.，2007）讨论了这些方程组的Saint-Venant 原理。文献（Franchi et al.，2003；Lin et al.，2007；Ciarletta et al.，2015；Cichon et al.2015；Chen et al.，2016；Liu，2017；Liu et al.，2018a；Liu et al.，2018b；李远飞，2019a；李远飞，2019b；李远飞等，2019；李远飞，2020）讨论了包括Brinkman、Darcy 和Forchheimer 方程组在内更多偏微分方程组的结构稳定性，获得了一些新的成果。本文我们考虑如下Brinkman方程组

其中ui，p，T，C分别为速度、压强、温度和盐浓度，gi(x)和hi(x)为重力函数且|gi|，|hi|≤1，∆为拉普拉斯算子，σ> 0是Soret系数，λ> 0是Brinkman系数。

方程组（1）在Ω ×[0，τ]内成立，其中Ω 是R3中有界单连通的凸区域，τ是固定的一个常数且0 ≤τ< +∞.我们所考虑的温度与盐浓度的边界是绝缘的，并且溶质通过边界的通量为0。其边界条件为

此外，初始条件为

本文研究了方程组（1）的解对Brinkman系数λ的连续依赖性。为了获得连续依赖性的结果，通常的做法是利用温度和盐浓度的最大值，去推导出交叉项的先验界，而本文方程组（1）的第4 个方程中含有温度的拉普拉斯项，该项的存在导致盐浓度C的最大值估计难度很大。为了克服这个难题，我们采用给出C的四阶范数的先验界。为了推导出到C的四阶范数的先验界而构造的函数是文中最大创新点。

1 先验估计

本节中将给出在后面定理的证明中所需的若干估计。

引理1 对于温度T，我们有如下估计

证明在方程组(1)的第3个方程两边同时乘以T2p−1，p≥1，并在Ω上积分得

且式（5）化为

即证明了式（3）。

在式（6）中取p= 1，有

则

证毕

引理2 对于盐浓度C，我们有如下估计

证明在方程组(1)的第4个方程两边同时乘以C，并在Ω上积分，由Hölder不等式和算术几何平均不等式得

引理3 对于盐浓度C，我们有如下的4阶范数估计

运用式（3），Hölder不等式和算术几何平均不等式，可得

其中ε1，ε2是大于零的任意常数。

运用方程组(1)的第3个、第4个方程以及Hölder不等式，可得

再运用式（3），Hölder不等式和算术几何平均不等式，可得

其中ε3，ε4是大于零的任意常数。

联合式（9）～（10），可得

其中k是大于零的任意常数。

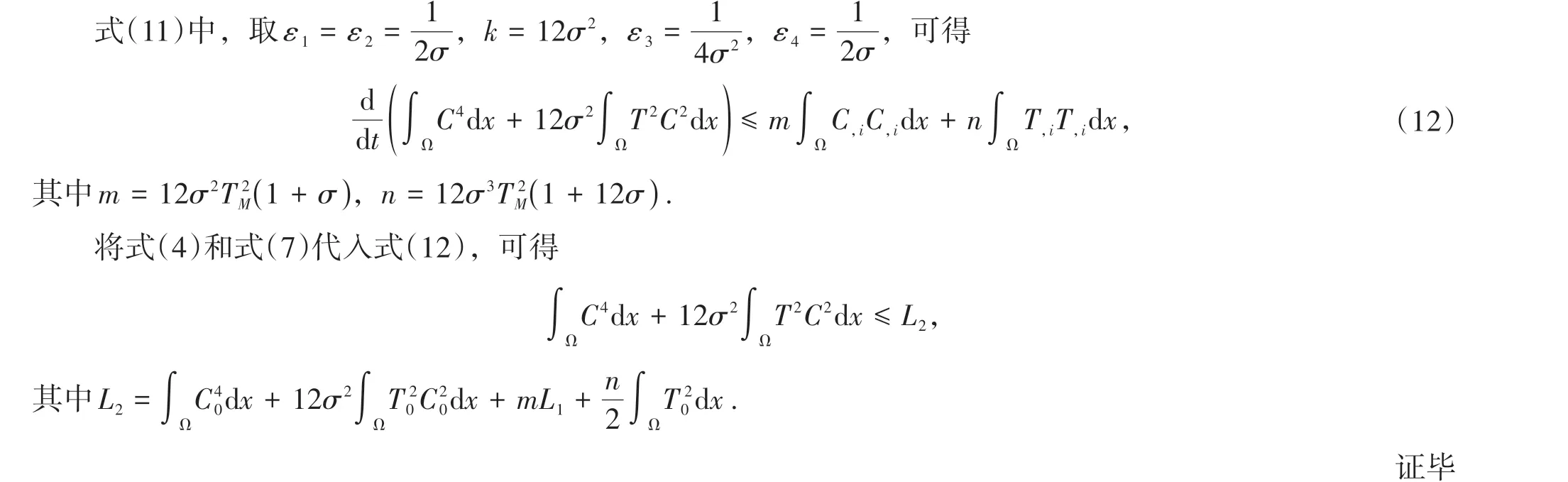
2 连续依赖性

假设(ui，T，C，p)是如下Brinkman方程组初边值问题的解

边界条件为

初始条件为

我们定义解的差为：ωi=ui−u*i，θ=T−T*，S=C−C*，π=p−p*，λ=λ1−λ2，则(ωi，θ，S，π)满足如下初边值问题

边界条件为

初始条件为

引理4 对于速度ui，有如下估计

证明 在方程组(13)的第1个方程两边同时乘以2ui，并在Ω上积分得

其中k1，k2，k3是大于零的常数。

证明 在方程组(19)的第1个方程两边同时乘以2ωi，并在Ω上积分，由式（20）、Hölder不等式和算术几何平均不等式，可得

对于满足在边界上为零的函数E，由文献（Flavin et al.，1995）的结论，我们有如下Sobolev不等式

其中c1，c2是大于零的常数。

在式（26）中，取E= ωi，可得

联合式（8）、（25）和（27），可得

注本文我们研究了流体模型的解对Brinkman系数λ的连续依赖性。利用文中的类似方法，依然可以建立方程组的解对其他方程系数的连续依赖性。接下来，将考虑在有界区域内方程组的解对边界系数的结构稳定性。由于本文中的方程含有∆ui项，通过该项较容易得到速度梯度的估计，接着我们将讨论不含有该项的情况，此时如何获取速度梯度的估计将会是面临的最大障碍，我们会在后续文章中进行研究。