应用可见光和近红外图像对白桦凋落叶碳质量分数的估测模型1)
张莹 董希斌 刘慧 高彤 任允泽 高然
(森林持续经营与环境微生物工程黑龙江省重点实验室(东北林业大学),哈尔滨,150040)
凋落物是陆地生态系统的重要组成部分[1],在森林土壤碳循环中起着重要的转化和驱动作用[2]。凋落物积累和分解速率高将加速整个生态系统的碳循环过程,相反若速率放缓则会在一定程度影响该地区的碳平衡[3-5]。实时监测和快速获取植物凋落叶的碳质量分数,可以及时推测凋落物的分解速率,有效掌握林业生态系统的环境状况和生长发展动态,同时也对估算植物凋落物碳储量具有重要意义。传统的植物碳质量分数检测一般只能在实验室完成,有干烧法和湿烧法两种。湿烧法是利用植物有机碳容易被氧化的性质,采用重铬酸钾外加热法测定[6],虽然精度较高,但费时费力,人为操作误差较大,由于进行分析时所必须使用的化学试剂(浓硫酸和重铬酸钾),还存在环境污染的风险。干烧法是利用元素分析仪进行测定[7],精度高于湿烧法,但设备价格昂贵,且需要专业的实验人员。
近年来,随着计算机视觉技术和机器学习的不断发展,利用图像信息实现元素质量分数预测的应用也变得越来越广泛。Furlanetto et al.[8]利用无人机搭载的可见和近红外数码相机的成像数据对玉米叶片钾元素(K+)缺乏进行了鉴定和定量研究;Damayanti et al.[9]利用数字图像数据和人工神经网络对木薯叶的叶绿素质量分数进行了预测研究;Zha et al.[10]利用机载多光谱相机的图像数据和其他相关的土壤、天气信息通过机器学习方法对水稻氮素进行了预测研究;Taneja et al.[11]利用手机采集图像信息对土壤有机质和土壤水分进行了预测研究;Ye et al.[12]利用对苹果树叶片的扫描信息实现叶片的氮和叶绿素浓度预测从而实现对苹果树营养状况的快速、无损的评估;Wang et al.[13]将普通相机通过替换光学滤光片的方式改装成可见光和近红外相机,并利用自制可见和近红外相机成像探究了植物叶片倾角对其叶绿素反演的影响;以及利用图像信息对水果成熟度[14-15]和可溶性固形物含量[16]、土壤密度、孔隙度和粗糙度[17-19]、玉米种子活力[20]等的预测研究。
然而,利用可见光和近红外相机获取凋落叶的图像信息对凋落叶碳质量分数进行预测方面的研究报道较少。因此,本研究以白桦凋落叶为研究对象,利用图像处理技术提取特征值并进行筛选,并通过回归分析建立白桦凋落叶碳质量分数预测模型,以确定机器学习在凋落叶碳质量分数预测中的可行性,为白桦凋落叶更直观和长期连续性观测提供了可能,同时也为凋落叶的碳质量分数估测提供了新的研究思路。
1 研究区概况
研究区位于哈尔滨市城市林业示范基地(东北林业大学),地理坐标为45°42′~45°44′N、126°35′~126°39′E,总面积约50 hm2,海拔136~140 m, 属于平原地带。试验区域气候属于温带季风性气候,土壤类型为黑土。本次试验研究样地为该林场内白桦(BetulaplatyphyllaSuk.)人工林区,该林地于1960年春以种植2 a实生苗建立,林木分布均匀,面积约0.5 hm2,林分年龄为65 a,含有白桦树493株,平均胸径20 cm。
2 研究方法
2.1 试验设计及数据采集
本试验样品采集于2022年10月中旬,为白桦叶凋落季节。在样地内按五点取样法,选择5个5 m×5 m的样方,将凋落叶层分为上层、中层和下层,并在样方内随机采集凋落叶10~15片,然后将采集的凋落叶按片用牛皮纸袋平整装好并编号,带回实验室,用于叶片的图像采集和碳质量分数测定。
试验使用两款感光传感器均为OV2710,最低照度为0.051 lx,具有200万像素的工业摄像头进行叶片图像采集,一款为普通可见光摄像头,一款为只允许700~1 100 nm波长光线透过的近红外摄像头。在植物取样的同一天,进行叶片图像采集。将单个叶片正面朝上放置在水平拍摄台铺设的白纸上面,两款摄像头并列安装在拍摄台上方大约25 cm处的支架上,调整支架,使镜头的方向与拍摄台保持垂直,逐一放置样品,并通过计算机编程语言Python软件编程控制,同时拍摄叶片的可见光和近红外图像存储在计算机中,保存为JPG格式并完成图像编号(图1)。图像采集完成后,将叶片重新放回带有编号的牛皮纸袋,放入烘箱内105 ℃杀青15 min,然后在65 ℃恒温条件下烘干24 h至恒质量,研磨后过60目筛,采用德国总有机碳/总氮分析仪(analytikjena Multi N/C2100S)测定。

图1 不同叶片的可见光和近红外图
2.2 图像预处理和特征值提取
对采集到的图像进行预处理,从而获取特征数据矩阵,主要流程如图2所示。利用Python软件分别将可见光图像和近红外图像转化成灰度图像,然后通过最大类间方差法(OTSU)将灰度图像转化成二值图像进行阈值分割,并进行轮廓筛选获得叶片轮廓,最后将感兴趣区域(ROI)切割出来得到单叶图像。
图像分割后,首先将可见光图像进行彩色模式转换,把光学三原色(RGB)图像转换成六角椎体模型(HSV)图像和灰度图像,然后将近红外图像,进行图层分离,选取波长最大的波段图层作为近红外波段像素,并计算图层均值(INIRmean),最后从RGB、HSV和单色图像中提取叶片颜色、纹理和形状特征,形成表1所示的数据集。图像的颜色特征用颜色距和各波段图层均值运算来表达,其中颜色矩主要包括RGB图像的红(R)、绿(G)、蓝(B)三分量、HSV图像的色调(H)、饱和度(S)、明度(V)三分量以及灰度图像的灰度分量的一阶矩、二阶矩和三阶矩。纹理特征则利用灰度图像生成灰度共生矩阵来描述,基于灰度共生矩阵构建统计量,本研究选择能量、对比度、最大概率值、逆差分矩、差异分差、熵作为叶片图像的纹理特征值。叶片的形状特征从二值图像中提取,选取叶片面积、叶片轮廓周长、叶片边界矩阵长宽比、最小外接矩阵长宽比、叶片面积与边界矩形面积比、轮廓面积与凸包面积比、圆形度、矩形度作为叶片的形状特征参数。

图2 最大类间方差法(OTSU)分割过程图

表1 图像特征参数
2.3 模型选择
人工神经网络是一种基于生物神经系统,模拟神经细胞接收、处理和传导信号机制的运算模型[21]。人工神经网络由各种类似神经元结构的单元通过相互连接构成,每个神经元都包含一个偏差(θ),当接收到的输入信号通过权值(w)进行线性加权运算后,通过激活函数(f)变换获得输出值y(公式1),其中激活函数经常使用S型生长曲线(sigmoid),从而有利于解释输入和输出变量之间的非线性。一般来说,一个人工神经网络可以划分为3个层,分别是输入层(a),隐藏层(b),输出层(c)。
(1)
式中:y为该神经元输出值;xi为输入信号;wi为权值;θ为偏差;f为激活函数。
将特征向量作为输入层进行上述计算后不断传播计算到输出层,并与样本值作比较,计算误差,然后根据梯度下降法向前计算偏导数来更新各层的偏差和权重,反复计算后使输出误差达到很小值为止。本研究利用MATLAB软件构建简单的3层神经网络,将处理后的叶片图像特征值作为输入层,叶片的碳质量分数作为输出,由于隐藏层的数量会影响模型的时间和性能,所以隐含层的神经元数量通过试差法确定。同时为了得到更好的网络初始权值和偏差,选用遗传算法对神经网络进行优化。
支持向量回归模型是在支持向量机的基础上对回归任务进行优化,适用于解决高维特征的回归问题[22]。该算法用于在高维空间寻找超平面来最小化误差,同时引入不敏感损失系数ε,当预测值与观测值的绝对差值不大于ε时,认为损失值为0,从而最大化预测值和观测值之间的边际。此外在支持向量回归模型中还可以应用各种核函数,帮助解决各种线性和非线性回归问题。本研究利用Python软件构建了3种不同核函数的支持向量回归模型,包括径向基核函数、线性核函数、多项式核函数,并比较不同模型对叶片碳质量分数的预测能力。
随机森林是一种基于决策树和装袋算法结合的集成学习模型[23]。该算法通过对样品数据集进行有放回随机抽样,产生多个与原始数据集容量数相同的不同数据子集,再将这些新数据集以并行模式构建多棵决策树,每棵决策树通过不断分化计算产生对应的回归预测数据,最后将不同回归树返回的预测数值进行均值计算(公式2),得到最终的回归预测结果。有放回的随机抽样和决策树并行集合,提高了随机森林模型对噪声的容忍度。在随机森林中,决策树个数、最大深度、最小叶子节点样本数和最大分离特征数都是需要优化的模型超参数,因此,为了定义最佳参数,本研究利用Python语言中的Sklearn模块对随机森林模型的超参数进行自动优化,寻找最佳预测模型。
(2)

2.4 模型评价
试验共获取207组数据,随机选取80%的数据作为训练集,20%的数据作为测试集。为了对所建立的预测模型性能进行准确评判,本研究选取平均绝对误差(EMA)、均方根误差(ERSM)、平均百分比误差(EMAP)和决定系数(R2)作为评价指标,公式如下:
(3)
(4)
(5)
(6)
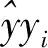
平均绝对误差(EMA)、均方根误差(ERSM)、平均百分比误差(EMAP)越小,表明回归模型的预测精度越高,R2值越高表明预测值和实际值之间相关性越大,两者拟合度越好,即预测性能越好。
3 结果与分析
3.1 变量选择
对从叶片图像中提取的47个特征变量进行相关性分析,并绘制相关系数矩阵热力图(图3),可以从图中看出部分自变量之间相关性比较大,直接使用全部变量建模容易引起多重共线性问题,影响模型的稳定性。

图3 特征变量相关系数热力图
本研究采用主成分分析算法,将原始特征变量通过正交变换转化成互不相干的综合变量,并计算各综合变量的累计方差贡献率(图4),同时为了尽可能的保留数据信息,对原始特征变量进行降维,最终选取前7个主成分(累计方差贡献率达92%)作为新的特征变量。

图4 主成分累计方差贡献率
3.2 预测模型的建立和性能评估
3.2.1 遗传算法优化神经网络模型(GA-BPNN)
将主成分分析降维后的7个特征变量作为输入层,叶片碳质量分数作为输出层,隐含层层数为1,根据隐含层节点个数的经验公式(公式7)对训练集进行神经网络训练,计算不同隐含层节点数的训练集均方误差,由图5可知当节点数为11时,均方误差最小,因此确定隐含层节点个数为11。为了得到更好的网络初始权值和偏差,选用遗传算法对神经网络进行优化,设遗传算法的迭代次数为30,种群数为17,染色体的选择方法为轮盘赌法,编码方式为二进制法,交叉概率取0.7,变异概率取0.1,选择166组训练样本的预测值与期望值的误差矩阵的范数作为适应度值的目标函数,得到最佳的初始权值和阈值矩阵。然后利用训练集样本对遗传算法优化的神经网络进行训练,设训练次数为10 000,学习率为0.1,动量系数为0.3,误差阈值为0.000 001,建立叶片碳质量分数预测模型;再利用测试集样本对预测模型进行验证。基于遗传算法优化神经网络的叶片碳质量分数预测模型效果和预测结果如表2、图6所示。
(7)
式中:h为隐含层的节点个数;a和b为输入层和输出层节点的个数;c通常取 1~10的整数。

图5 隐含层节点数寻优结果

表2 GA-BPNN神经网络模型建模及预测结果
由表2可知,GA-BPNN模型对叶片碳质量分数的预测效果较好,在训练集上平均绝对误差EMA、均方根误差ERSM、平均百分比误差EMAP和决定系数R2分别为6.472 4、7.917 9、0.014 9和0.670 8,测试集上相应的统计指标值平均绝对误差、均方根误差、平均百分比误差和决定系数分别为7.508 1、8.671 3、0.017 2和0.533 9,说明该模型拟合程度较高,对叶片碳质量分数预测具有一定的实用价值。
3.2.2 支持向量机回归模型(SVR)
使用Python语言中的Sklearn模块构建3种不同核函数的SVR模型。对径向基核函数模型(RBF-SVR)和多项式核函数模型(Poly-SVR)中的函数系数(γ)和惩罚因子(C)进行网格搜索寻找最优参数,其中参数gamma的搜索数组为{0.01,0.05,0.1,0.15,0.2,0.25};C的搜索范围为(1,10),步长为1。实验结果表明:径向基核函数模型的最优参数组合为函数系数(γ)=0.05、C=10;多项式核函数模型的最优参数组合为函数系数(γ)=0.05、C=1。对于线性核函数模型(Linear-SVR),无需对相关参数进行设置,均使用默认参数。采用实验获取的各模型参数最优值,对训练集数据进行模型训练,并对测试集进行验证。建模和预测结果如表3、图7所示。
从表3可知,Linear-SVR模型预测效果较好,训练集和测试集决定系数R2均大于0.5,说明模型预测值与真实值拟合结果较好;Poly-SVR模型虽然训练集的决定系数达到了0.662 0,但测试集决定系数为0.482 5,预测效果不佳,说明模型泛化能力较弱;与上面两个模型相比,RBF-SVR模型的拟合效果最好,训练集和测试集的EMA分别为4.151 9和6.529 2、ERSM分别为6.624 4和7.925 2、EMAP分别为0.009 6和0.015 0,统计指标值均为最小,且训练集决定系数达到了0.769 6,测试集决定系数达到了0.610 7,模型稳定性较强。
3.2.3 随机森林回归模型(RFR)
因随机森林回归模型中超参数较多,本研究选用交叉验证和网格搜索对参数进行寻优。其中决策树的数量(n_estimators)搜索范围为(50,150),步长为10;每个叶子结点包含的最小分离样本数(min_samples_leaf)搜索范围为(1,7),步长为1;决策树最大深度(max_depth)搜索数组为{1,5,10,50,100},最大特征数(max_features)搜索数组为{‘auto’,‘sqrt’,‘log2’},交叉验证(CV)值取15。利用训练集对模型进行训练,并根据训练样本的得分确定随机森林模型的最优参数。各参数网格搜索得分结果如图8所示,得到最佳的参数组合为n_estimators=80,max_features=‘auto’,min_samples_leaf=1,max_depth=5。

表3 3种支持向量机回归模型建模及预测结果
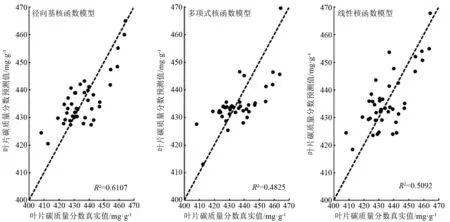
图7 3种支持向量机回归模型测试集的预测值与真实值散点图
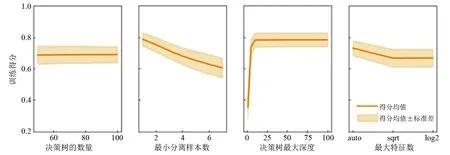
图8 随机森林模型参数网格搜索得分结果图
采用实验获取的模型参数最优值,对训练集数据进行模型训练,并对测试集进行验证。建模和预测结果如表4、图9所示。

表4 随机森林模型建模及预测结果
从表4结果来看,在训练数据集上,RFR模型对叶片碳质量分数的拟合和预测效果最好,平均绝对误差EMA、均方根误差ERSM、平均百分比误差EMAP和决定系数R2分别为4.625 3、5.608 7、0.010 6和0.834 8;测试集拟合结果低于训练集拟合结果,测试集决定系数仅为0.521 8,但R2大于0.5,说明该模型可以在一定程度实现对叶片碳质量分数的预测。
4 结论
通过大津算法和彩色图像模式转化对可见光和近红外摄像头拍摄白桦凋落叶的图像进行预处理,提取RGB、HSV和单色图像中的叶片颜色、纹理和形状特征,并利用主成分分析对提取到的47个特征变量降维,将降维后的7个新的特征变量作为GA-BPNN模型、SVR模型、RFR模型的输入,构建的不同模型并进行对比分析。在训练数据集上,RFR模型对叶片碳质量分数的拟合和预测效果最好,平均绝对误差(EMA)为4.625 3,均方根误差(ERSM)为5.608 7,平均百分比误差(EMAP)为0.010 6,决定系数(R2)达到了0.834 8;在测试数据集上,RBF-SVR模型相比于GA-BPNN模型、RFR模型和其他核函数的SVR模型拟合和预测效果最佳,其平均绝对误差(EMA)、均方根误差(ERSM)、平均百分比误差(EMAP)和决定系数(R2)分别为6.529 2、7.925 2、0.015 0和0.610 7,与其他模型相比统计指标值均为最小。从训练集和预测集的综合表现来看,RBF-SVR模型可预测该区域的白桦凋落叶碳质量分数,为推测凋落物的分解速率提供了新方法。

图9 随机森林模型测试集的预测值与真实值散点图

