空间目标监视雷达电波折射修正方法

闫永宝,陈 亮,刘小东,欧 明

(1. 61191部队, 杭州 310023; 2.中国电波传播研究所, 山东 青岛 266071)

0 引言

空间目标监视雷达主要用于目标的搜索、捕获和跟踪[1]。随着科学技术的发展,空间目标监视雷达的测轨能力需求进一步提升,随之对其探测精度提出了更高的要求,电波环境主要影响雷达系统的探测精度和目标成像等。空间电波环境主要包括对流层和电离层,对流层对雷达电波传播的影响与对流层大气压强、温度、湿度,对流层折射率等有关;另外,对流层中存在着大气的湍流运动,其对雷达电波的传播造成严重影响。电离层分为背景电离层和电离层暴,对于位于南方地区的雷达,电离层垂直延迟一般最大为30TECU,则在2 000 km的探测距离上电离层延迟造成的测距误差约为6 m。对于存在电离层暴时的电离层垂直延迟最大约为65TECU,在2 000 km的探测距离上电离层延迟造成的测距误差可以达到约13 m。当目标位于低仰角时(以10°仰角为例),上述电离层延迟误差将分别增大至约35 m和74 m。此误差已超出系统测量的精度要求;另外,电离层发生扰动时,将会对雷达系统的目标探测能力产生影响,因此雷达电波折射修正尤为重要。需要提出更好的方法修正折射造成的误差。文献[2]利用GPS实测观测值在不同卫星截止高度角情况下获得的斜路径总电子含量作为参考,对该电离层模型性能进行评价,结果表明,模型的斜向总电子含量与实测差值的标准差保持在15TECU以内,但其F10.7为月均值;文献[3-9]对不同电离层模型精度进行了分析,但未提及模型驱动和折射修正;文献[10]对高轨道目标电离层折射修正方法进行了研究,未提及模型驱动及仰角修正;文献[11-13]研究了大气折射对雷达电波折射的影响及校正,未涉及到电离层的修正;文献[14]采用我国大气折射率,进行目标定位误差分析,为高精度中近程雷达的俯仰测角修正提供了参考数据,但对流层模型未采用实测数据驱动。

论文综合考虑对流层和电离层对空间目标监视雷达的影响,采用气象测量数据和BD/GPS实测数据驱动更新模型以此来提高空间目标监视雷达电波折射修正精度。

1 对流层折射率及模型驱动更新

1.1 对流层折射率

大气折射率N与大气气象参数(包括压力P、大气温度T、水汽压ew)有关,可表示为:

(1)

式中:第1项为干项,表示干空气的影响;第2项为湿项,表示水汽的影响。对流层折射率干项较为稳定,折射率的变化主要是由空气中的湿度变化引起的,折射率湿项约占整个折射率的10%左右。电波传播的折射误差主要是由折射率干项引起的。

对流层大气作为电波的传播介质,对电波传播的影响由折射指数n或折射率N体现,大气的折射指数n接近于1,N与折射指数n的关系为:

N=(n-1)×106

(2)

对流层参量测量主要采用气象采集仪直接获取,可输出地面温度、湿度、气压等气象数据。结合气象采集数据与雷达所处地理位置特点,可计算得到观测站的地面折射率。

1.2 对流层模型驱动更新

结合气象采集数据与雷达测站地理位置特点,对流层模型拟采用分段模型,即地面到1 km处采用线性模型,1～9 km、9～60 km分别采用不同指数模型:

(3)

式中:N0为地面折射率(N);hs为地面海拔高度( km);ΔN1为近地面1 km内的折射率负梯度(1/ km);N1为地面1 km高度处折射率;c1为地面以上1 km至海拔9 km的指数衰减率(1/ km);N9为海拔9 km高度处折射率,该值很稳定,大多数地区均可取为105 N单位;c9为海拔9～60 km的指数衰减率(1/ km)。国军标GJB1655给出了我国的c1,c9和N9的全国年平均值分别为0.125 8/km、0.143 4/km、105.6 N单位。

该模型是整个低层大气的精确平均模型,其中N0、ΔN1、c1和c9为待定参量,由于对流层折射率剖面分段模型是连续的,模型隐含存在下面的关系:

(4)

搜集雷达测站处的历史气象探空数据,利用数值算法拟合得到分段模型的参数:N0、ΔN1、c1和c9。对流层模型驱动更新如图1所示,通过历史气象探空数据拟合计算出4个参数,然后由地面气象站数据得到地面折射率N0,结合前述计算的ΔN1、c1和c9,即可驱动对流层模型。

图1 对流层模型驱动更新方法

2 电离层模型及驱动更新

电离层采用NeQuick经验模型,考虑到此模型精度有限,修正剩余40%左右,采用BD/GPS双系统实测数据驱动NeQuick模型,提高模型精度。

由实测TEC数据驱动的NeQuick模型更新过程的主要数据处理包括:

1) 实测电离层延迟获取

由原始观测数据计算接收机至卫星倾斜路径上的电离层延迟。

2) 模型参量的搜索更新

利用NeQuick模型,获取相同路径上的倾斜电离层延迟,通过使模型TEC与实测TEC误差最小化,利用最优化算法确定模型中的参量。在基地观测站中,由该站点特定时间段内BD/GPS接收机观测值与NeQuick模型输出的TEC值间的平方误差最小,得到最优化的Az指数,具体表述为:

(5)

式中:n为单个观测站一天对所有卫星的观测数目;TECMeasured是利用BD/GPS观测对区域电离层模型TEC估计值;TECNeQuick(Az)为NeQuick模型计算值。

以NeQuick模型TEC计算值误差平方和最小为基准,对有效参数Az进行估计。Az是将太阳活动水平引入NeQuick模型的重要参数,它是驱动NeQuick模型计算的重要因子。原有模型中Az取值为64～193,与F10.7相同。但研究表明Az和F10.7相关性并不强。将其取值扩大至0～209,可有效提高模型精度。

3) 电离层模型更新

基于上述更新的电离层模型参量,实现对电离层模型的更新,重构出空间任意点处的电离层电子密度分布。电离层模型更新方法如图2所示。

图2 电离层模型驱动更新方法

4) 电离层折射率剖面生成

利用更新后的电离层模型,获取雷达至目标处的电离层折射率剖面。

3 电波折射修正方法

雷达电波折射修正主要采用球面分层法计算电波环境的折射误差,球面分层法是基于大气结构的水平均匀分布,根据几何光学原理和射线方程给出距离、仰角、速度等误差的计算方法。如下式所示,利用射线描迹方法获得任意方位、仰角、距离上的电波修正参数,雷达电波折射示意图如图3所示。折射计算方法如图4所示。

图3 雷达电波折射

图4 折射误差计算方法

当目标位于大气层内时视在距离为:

(6)

当目标位于电离层内时视在距离为:

(7)

地心张角为:

φ=

(8)

由上式联合计算得到电波折射误差如下式所示,真实仰角:

(9)

仰角误差为:

ε0=θ0-α0

(10)

真实距离为:

(11)

距离误差为:

ΔR=Ra-R0

(12)

式(12)中:n为折射率;a为地球半径;R0为目标真实距离;Ra为目标视在距离;h0为雷达高度;hT为目标高度;φ为雷达与目标对地心的张角;cosα0为目标真实仰角;θ0为雷达视在仰角。

4 实验结果

4.1 对流层模型验证

利用University of Wyoming获取的杭州地区1998—2010年11月气象观测数据进行建模。

LT∶00∶00时刻结果如图5、图6所示。初始N0=317.1、ΔN1=43.9、c1=0.122 4和c9=0.138 1;从图5可看出,Err=3.9 N,RMS=5.6 N,从统计误差可看出。折射率误差小于5 N占比95.4%,折射率误差小于10 N占比98.6%。LT∶12∶00时刻结果如图7、图8所示。初始N0=313.9、ΔN1=41.0、c1=0.122 2和c9=0.137 9;从图7可看出,Err=4.3 N,RMS=6.2 N,从统计误差可看出,折射率误差小于5 N占比94.0%,折射率误差小于10 N占比98.1%。

图5 LT∶00∶00时刻折射率驱动结果

4.2 电离层模型验证

利用前一天的垂直观测数据(时间分辨率为15 min),驱动NeQuick模型,得到的模型值与当天的斜TEC观测值(时间分辨率为15 s)进行比较。图9为前一天观测站的垂直观测数据。图10为前一天观测站垂直电离层TEC数据驱动电离层NeQuick模型得到的模型值与当天的斜TEC观测值(时间分辨率为15 s)的比较结果。红线为模型结果,蓝线为观测结果。

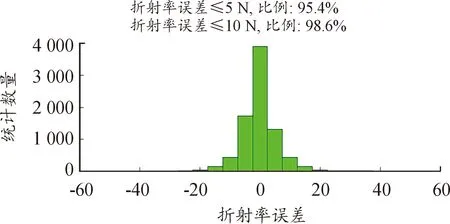
图6 LT∶00∶00时刻折射率误差

图7 LT∶12∶00时刻折射率驱动结果

图8 LT∶12∶00时刻折射率误差

图9 观测站电离层TEC垂直观测数据

图10 观测站电离层模型值与观测值对比结果

图11为当天观测站电离层TEC模型值相对误差的累计概率曲线。从图可知,电离层驱动模型的修正相对误差为20%(1σ),即相对精度为80%(1σ)。图12为当天观测站电离层TEC模型值绝对误差直方图。从图可知,电离层驱动模型的修正绝对误差平均值为-0.74TECU,标准差为2.65TECU,RMS为2.76TECU。

图11 观测站电离层TEC模型值相对误差累计概率

图12 观测站电离层TEC模型值绝对误差直方图

4.3 雷达电波折射修正验证

按照论文所述的对流层和电离层模型及驱动更新方法计算对应的折射率剖面,结合图4所示流程,以2020年2月和3月共76条标校星测量数据为例,利用日本实验测地卫星、法国JASON2卫星和美国JASON3卫星共3种精密卫星星历对修正前后的雷达测量数据精度进行仿真分析评估,电离层上限高度约1 000 km,3颗卫星轨道高度均穿透整个对流层和电离层,误差统计计算方法按照文献[15]所述方法。通过仿真计算,结果如表1所示。

表1 雷达电波折射修正验证结果

5 结论

论文提出的电波折射修正方法通过仿真实验结果表明,雷达斜距测量误差平均减小量36.9%,仰角测量误差平均减小量24.3%。该方法已在某型雷达中进行了工程应用,与原系统经验公式修正相比,修正效果明显,与仿真结果一致,具有推广应用价值。