纳米颗粒对超临界二氧化碳流体传热特性的影响
代 威,刘丽丽,杨 智,廖传军,陆浩然
(1.北京宇航系统工程研究所, 北京 100076;2.西安航天神舟建筑设计院有限公司北京分公司, 北京 100040;3.广东工业大学 材料与能源学院,广州 510006)
0 引言
以超临界CO2为工质的布雷顿循环[1-2]是一种经济且高效的热力循环,兼具气体布雷顿循环和蒸汽朗肯循环的优点,透平入口温度高,压缩功消耗少,理论上具有更高的系统热效率,同时系统运行压力相对较高,工质密度大,属单相传热,系统简化且结构紧凑[3]。目前,超临界CO2布雷顿循环在核动力发电[4-5]、高温太阳能发电[6-7]、太阳能空调与热泵系统[8]及废热回收[9]等领域受到广泛关注。
通常,换热工质在换热器内的传热特性对系统的热力性能具有显著影响。如图1,超临界CO2在临界点或拟临界点附近具有显著的变物性特征。温度和压力的微小扰动即可引起CO2密度、热导率和粘度等热物性的剧烈非线性变化[10]。当超临界CO2布雷顿循环工作在跨临界温区时,换热流体热物性的显著变化则会引起高热流或低质量流率条件下极高的壁温峰值和极低的对流换热系数,也即传热恶化现象[11]。Kurganov等[12]研究发现竖直管内超临界CO2流体在管道截面上的M型速度分布对近壁区湍流的生成会形成抑制作用,进而造成传热恶化。Jackson等[13]研究表明,随温度逐渐偏离拟临界点,CO2密度急剧减小,进而诱发换热流体不同程度的浮升力和加速度效应[14],使得近壁区剪切应力减小,层流现象强化,进而导致局部传热恶化。吴新明[15]通过实验研究表明,超临界CO2质量流量较低时,换热管进口处会出现明显的壁温峰值,也即传热恶化;而增大质量流量后,壁面温度降低,且壁温峰值消失,传热系数随沿程变化出现微小波动,即传热模式由传热恶化向正常传热转变。Zhu等[16]研究表明,即使在高超临界压力条件下,较低的质量流率或较高壁面热流也会引起传热恶化现象。因此,如何有效规避超临界流体的传热恶化问题并充分利用其传热强化特性,对能源的高效转换与利用具有重要意义。
为抑制超临界流体传热恶化,国内外学者常采用管内插入扰流板[17]、扭带[18]、螺旋线[19-20]或表面粗糙化[21]等技术改变管内流体流动形态,强化流动剪切与微团混合,进而引导漩涡或二次流生成。然而,随着热边界层的发展,传热恶化现象仍会在湍流发生器的下流流道内出现。此外,湍流发生器的引入甚至会导致更多壁温峰值的出现,也即局部传热恶化[22-23]。

图1 (a)p=7.4 MPa时,超临界二氧化碳热物性 随温度的变化关系图;(b)不同压力下,超临界二氧化碳 比热容随温度的变化关系图
若采用少量纳米尺度固态颗粒均匀稳定分散于超临界二氧化碳流体中,由此混合而成的纳米悬浮液将极具强化传热潜力。自美国Argonne国家实验室Choi等[24]首次提出纳米流体概念以来,其强化传热特性已引起广泛关注[25]。纳米颗粒对超临界二氧化碳流体潜在的强化传热机制主要有:① 由经典Maxwell理论模型可知,通过添加高导热率固态纳米颗粒,如金属纳米颗粒,碳纳米材料等,可显著提高体相流体热导率;② 通常固态纳米颗粒密度远大于超临界二氧化碳流体,即使纳米颗粒比热Cp与其相当,其混合后则体积热容量整体上得以提高,且拟临界点处比热的突变特征也将趋于缓和;③ 与液相相比,超临界态二氧化碳密度和粘度较小,离散纳米颗粒随机碰撞也更为频繁,强化了纳米颗粒所携带的动量与能量在体相空间地传递。由此可见,纳米颗粒在超临界CO2流体传热特性强化方面可发挥重要作用。然而,目前有关纳米颗粒对超临界CO2流体流动传热特性的影响研究仍鲜有报道。
因此,本文将着重于纳米颗粒掺杂对超临界CO2流体热物性的影响,进而采用CFD数值模拟方法,探究不同纳米粒子体积分数、壁面热流等因素对超临界二氧化碳基纳米流体水平管内传热特性的影响,从而为纳米颗粒在超临界二氧化碳传热流体中的应用提供重要参考。
1 物理模型与计算方法
1.1 物理模型及网格划分
三维换热管进出口管径为D=6 mm,管长L=500 mm。本文采用ICEM网格生成软件进行O型结构化网格划分,且保证网格质量在0.7以上。由于近壁面处存在边界层效应,本文对近壁面处的网格进行了加密处理,以保证壁面附近的无量纲壁面距离(y+)小于1,网格生成效果如图2所示。
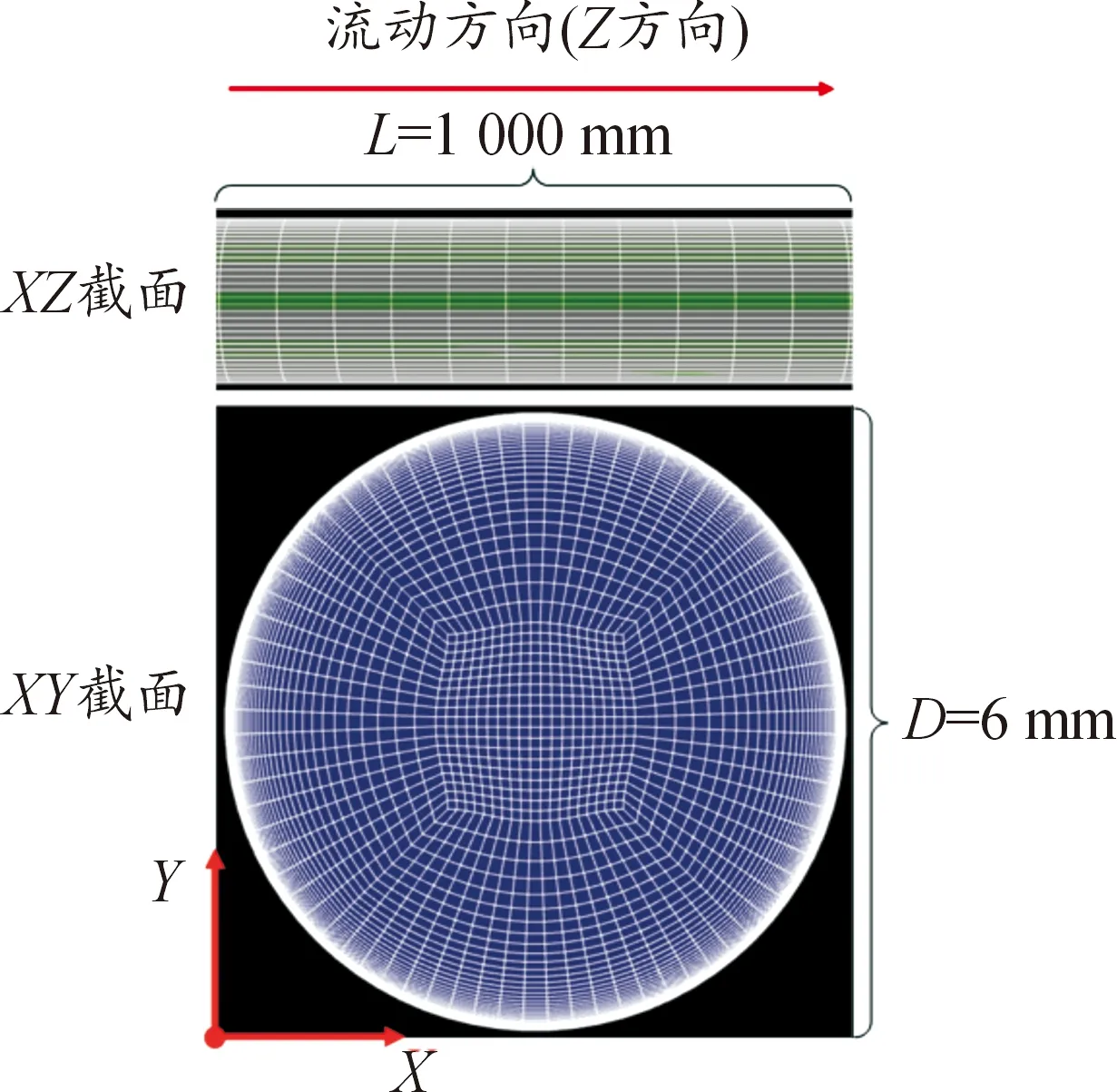
图2 水平换热管物理模型及网格划分
针对湍流流动,本文采用标准的k-ε模型进行数值计算,同时采用 SIMPEC 算法求解速度与压力的耦合方程,采用 QUICK 格式离散动量和能量方程,湍动能和耗散速率方程的离散采用二阶迎风格式。数值模型的控制方程如下所示:
质量方程:
(1)
动量方程:
(2)
能量方程:
(3)
湍动能k方程:
(4)
耗散率ε方程:
(5)
其中,
式中:δij为克罗内克函数;μ为动力黏度;μt=ρCμk2/ε为湍流黏度;k为湍动能;ε为耗散速率;λ为热导率;β为热膨胀系数;σk和σ分别为湍动能和耗散速率对应的湍流Prandtl数;c1、c2、Cμ、Prt为模型经验常数,湍流模型参数设置与参考文献[26]一致。
1.2 边界条件及网格无关性验证
为确保数值模拟计算的准确性,本文进行了网格无关性验证,且用于对比的网格数分别为196 000、468 550、924 000、1 522 500、2 655 500。在进行网格无关性验证中,选用8 MPa下的纯CO2流体作为研究对象,且流体入口质量流量为G=300 kg·m-2·s-1,壁面热流密度为q=10 kW·m-2。不同网格数下模拟所得的出口截面壁面温度(Tw,o)对流传热系数(ho)如表1所示。

表1 网格无关性验证结果
此外,本文数值模拟均为稳态模拟,采用质量流量入口边界条件,流量G=300 kg·m-2·s-1,且速度垂直于入口截面。采用压力出口边界条件,出口绝对压力为p=8 MPa,壁面为无滑移设置,给定恒定热流密度q=10-80 kW·m-2。
1.3 纳米流体热物性
纳米颗粒材质为Al2O3,纳米流体采用常用的均质混合物模型,也即仅考虑所添加纳米颗粒对流体热物性的影响。纳米流体热物性计算关联式如表2所示。本文中,纳米流体热物性随温度的变化关系均采用分段多项式进行拟合,并通过UDF加载到Fluent数值模拟软件中进行计算。

表2 纳米流体热物性计算关联式
2 结果分析与讨论
2.1 纳米流体物性随温度的变化规律
当压力为8 MPa时,纳米流体热物性随纳米粒子体积分数的变化关系如图3(a)—图3(d)所示。可见,随体积分数的增大,相同温度下纳米流体的密度、粘性和热导率均逐渐增大,而比热容呈略微减小趋势,且流体密度在高于320 K的区间内增长较显著,而热导率在310~340 K内增长较为显著,粘性和比热容在整个温度区间内变化较微弱。

图3 Al2O3-sCO2基纳米流体热物性随纳米粒子体积分数和温度的变化关系
2.2 变热流密度
由图4和图5可知,忽略入口效应(L<120 mm),入口质量流量G=300 kg·m-2·s-1,热流密度q=10 kW·m-2时,流体体相温度Tb在沿程方向上呈近似线性增长。这主要由于在低热流密度下,Tb仍远离拟临界点温度(对于纯二氧化碳流体,p=8 MPa时对应的拟临界温度点为307.85 K),比热容变化不显著。同时,随纳米粒子体积分数的增大,Tb升温速率加快,这主要由于流体比热容随体积分数增大而增大,从而加快了壁面热流向体相流体的传递。对壁面温度Tw而言,当体积分数为1%时,其壁温在沿程方向上均最小,其传热温差因此最小,壁面对流换热系数最大,如图5所示。在管内对流传热过程中,流体密度的增大使得相同质量流量下的入口速度下降,传热恶化。而热导率增大可强化壁面热流向体相空间的传递。因此,对于体积分数为1%的纳米流体,其热导率强化在传热过程中占据主导作用。
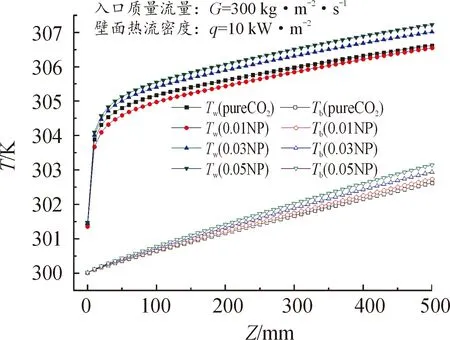
图4 当G=300 kg·m-2·s-1,q=10 kW·m-2时,体积分数 对沿程温度分布特性的影响
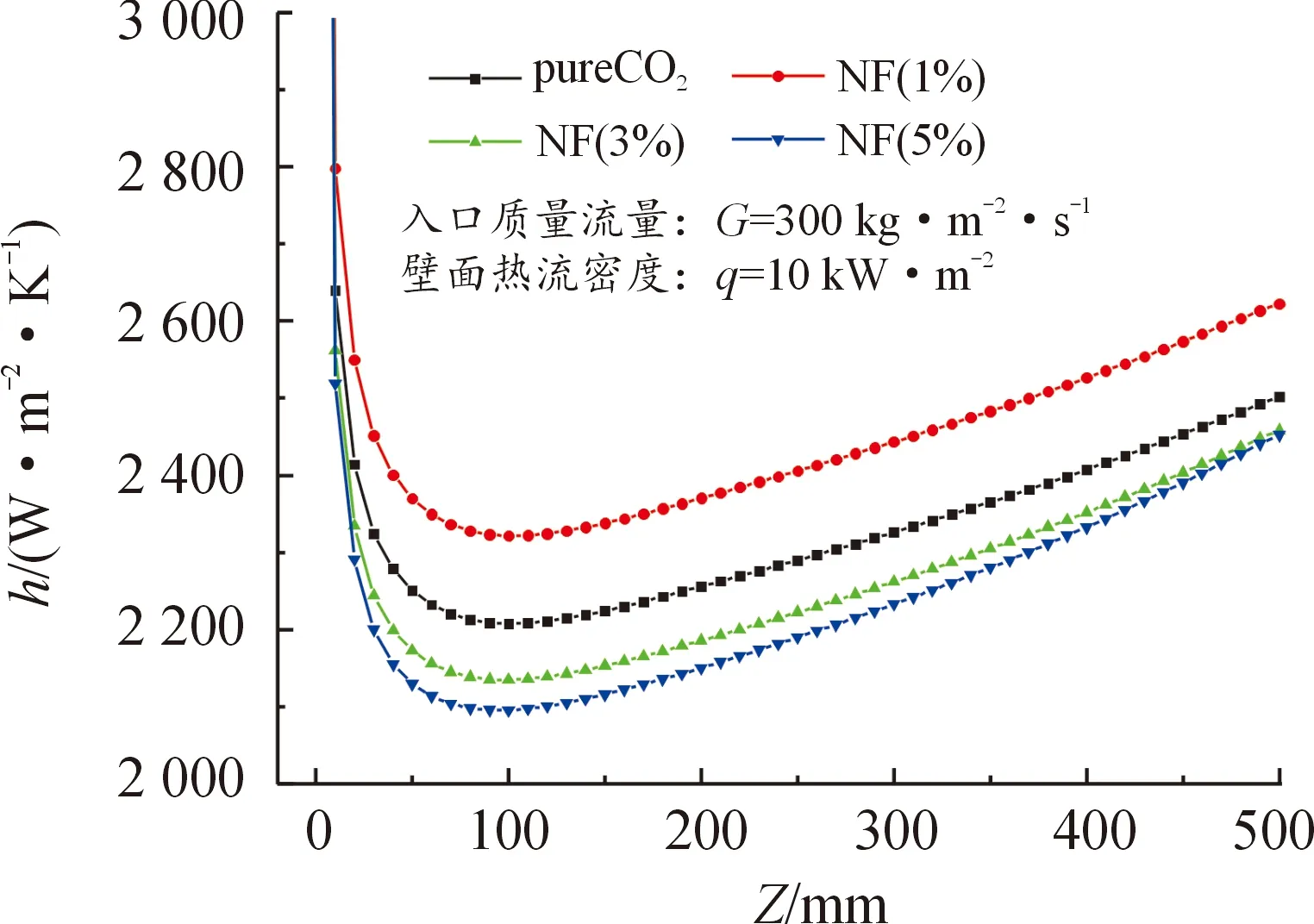
图5 当G=300 kg·m-2·s-1,q=10 kW·m-2时,体积分数 对沿程壁面对流换热系数的影响
由图6、图7可知,当热流q增大至30 kW·m-2,且体相温度Tb低于拟临界点温度时,Tb在沿程方向上同样呈近线性增长。但随着Tb逐渐趋近于拟临界温度点,其上升速率趋于平缓,这主要由于流体比热容在拟临界点附近急剧增大。同样,随着纳米粒子体积分数的增大,Tb上升速率加快。对Tw而言,在换热管前半段区间内(Z=120~250 mm),也即流动充分发展初期,随体积分数的增大,相同管段长度处的沿程Tw先增大后减小。这表明,在该热流密度下,流体热导率的增大相对于密度变化对壁温影响更显著。在换热管后半段,体积分数的增大,使得相同管长处的Tw也略微越大,同时管壁面沿程的升温速率更大,这主要由于近壁面处温度相对较高,体积分数的增大使得传热流体的比热容值下降,见图3(b)。由图7可知,在流体充分发展的管段内,随体积分数的增大,纳米流体具有一定的强化传热效果。

图6 当G=300 kg·m-2·s-1,q=30 kW·m-2时,体积分数 对沿程温度分布特性的影响Fig.6 Effect of volume fraction on the temperature distribution along the path when G=300 kg·m-2·s-1 and q=30 kW·m-2
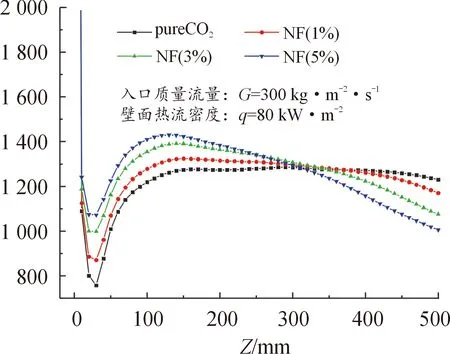
图7 当G=300 kg·m-2·s-1,q=30 kW·m-2时,体积分数 对沿程壁面对流换热系数的影响
由图8、图9可知,当热流q继续增大至50 kW·m-2时,体相温度Tb增长速率进一步加快。同样地,在拟临界点温度之前,Tb在沿程方向上呈近线性增长,在拟临界点附近变化趋于平缓。纳米粒子体积分数的增大,有助于壁面热流向体相空间传递,因此Tb相应更大。在流动充分发展初期的起始点处(Z=120),体积分数的增大,使得壁温逐渐减小,这主要由于纳米流体热导率逐渐增大且占据主要影响,使得壁面热量可以更快地向体相流体区传递。在后半段区间内,体积分数的增大,相同管长处的壁温越大,且在沿程方向上壁温的升温速率也越大,该现象与q=30 kW·m-2时类似,也即由比热容的减小所导致。由图9可知,在充分发展区内,对于纯二氧化碳和体积分数为1%的纳米流体,其壁面对流换热系数在沿程方向上逐渐增大,但增长速率逐渐减小;而对于更大体积分数的纳米流体,其壁面对流换热系数在沿程方向上先缓慢增大后急剧减下,这主要由于换热管后半段壁温的显著升高,而体相流体温度由于处于近临界点附近,其变化极为平缓,如图8所示。
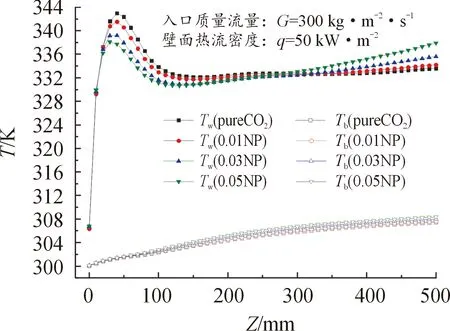
图8 当G=300 kg·m-2·s-1,q=50 kW·m-2时,体积分数 对沿程温度分布特性的影响
由图10、图11可知,当热流q继续增大至80 kW·m-2的高热流密度下,管段末端处的体相温度Tb逐渐偏离拟临界点,如图10所示。此时,随着纳米颗粒体积分数的增大,体相温度的升温速率也越快。总体上,体相温度的升温速率在沿程方向上呈先减小后升高的变化趋势。对壁面温度Tw而言,在换热管前半段(Z=120~300),随着体积分数的增大,其沿程壁温逐渐减小;在换热管后半段,随着体积分数的增大,其沿程壁温相比纯二氧化碳流体显著增大,该现象与q=50 kW·m-2时类似。由图11可知,在流体充分发展的管段内,壁面对流换热系数在沿程方向上呈单调减小的变化趋势,且随着纳米粒子体积分数的增大,其下降幅度更显著。此外,纳米粒子体积分数的增大,使得壁面对流换热系数在充分发展区的起始点处显著增大,而在管末端显著减小,在管段中间处交于一点。也即表明,在高热流密度条件下,纳米流体在流体充分发展区的初期具有显著的强化换热作用,但在后期换热恶化,其根本原因在于换热管后半段壁温的显著升高,如图11所示。

图10 当G=300 kg·m-2·s-1,q=80 kW·m-2时,体积分数 对沿程温度分布特性的影响
为了更好认知纳米粒子体积分数及热流密度对换热管对流换热系数的影响规律,本文进而在忽略入口效应前提下,也即不考虑L<120 mm管段的对流换热,对不同纳米颗粒体积分数和壁面热流密度的平均对流换热系数进行了对比,其中平均对流换热系数(have)通过对L≥120 mm管段的沿程换热系数平均取值获得,对比结果如图12所示。显然,have随热流密度的增大整体上呈逐渐减小的变化趋势。在热流密度q=10 kW·m-2时,have随纳米颗粒体积分数的增大呈先增大后减小的变化趋势,且在体积分数为1%时达到最大。当q增大至30 kW·m-2时,体积分数为1%时的have显著减小,4种体积分数下的have相当。当q继续增大至50 kW·m-2和80 kW·m-2时,have随纳米颗粒体积的增大呈单调性增大,也即纳米颗粒的增大可强化sCO2流体的管内换热特性。
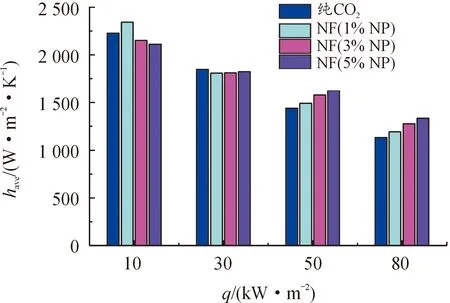
图12 忽略入口效应下,纳米粒子(NP)体积分数及 热流密度(q)对管段平均对流换热 系数(have)的影响
3 结论
本文采用CFD数值模拟方法,研究了不同纳米颗粒体积分数、不同热流密度对水平管内超临界二氧化碳纳米流体的传热特性的影响,主要得到以下结论:
1) 在低热流密度(q=10 kW·m-2),纳米流体体积分数为1%时,强化传热效果最佳。然而,随体积分数的继续增大,纳米流体传热性能恶化。当q=30 kW·m-2时,纳米流体在沿程均具有强化传热特性。当热流继续增大,纳米流体仅在流体充分发展的初期具有强化效果,在管段末端由于壁温的急剧升高而出现传热恶化现象。
2) 当流体体相温度Tb远离拟临界点温度时,其升温速率呈近线性变化。在拟临界点温度附近,流体体相温度Tb升温速率逐渐趋于平缓,其根本原因在于比热容的急剧变化。此外,随体积分数增大,沿程体相温度的升温速率也更快,这主要由纳米流体热导率的强化所致,使得壁面热流快速相体相空间。
3) 在高热流密度时(q=80 kW·m-2),流体对流换热系数在沿程方向逐渐减小,且其衰减幅度随纳米粒子体积分数的增大而逐渐增大,因此对于更长管段的换热,综合而言纳米流体不具有强化传热特性。
4) 在忽略入口效应时,have随热流密度的增大整体上呈逐渐减小的变化趋势。在低热流密度q=10 kW·m-2时,体积分数为1%所对应的have具有最大值,当q=50和80 kW·m-2时,纳米颗粒体积分数的增大可强化sCO2流体的换热特性。

