基于SPH算法的深松铲破坏土壤仿真模型
张志军,高奕珏
(常州大学环境与安全工程学院,江苏 常州 214500)
1 引言
土壤是影响农作物产量的关键因素。当前,我国某些地区土壤出现沙化现象,导致肥力下降,农作物减产。此外,长期使用化学除草方式,使土壤抗药性增强,生态环境恶化。近年来,土壤深松方法逐渐引入到农业生产中,土壤深松方法属于一种保护性耕作方法,不会改变植被与土粒结构。深松铲是完成该项技术的主要部件,它的主要能耗是克服土壤阻力做功。由于受阻力与功耗影响较大,还需进一步改进优化,同时深松作业涉及范围广,通过分析深松铲切削过程对土壤造成的影响,利用数值模拟方式获得土壤变化情况,为深松铲优化提供依据。
为实现深松铲破坏土壤的仿真,马跃进[1]等人提出基于离散元法的深松铲减阻效果仿真分析。在深松铲顶部设置减阻降耗的凸圆刃,利用非线性黏结弹性塑性接触模型构建土壤仿真模型,通过插件将颗粒和深松铲接触作用力导出,完成深松铲耕作阻力仿真。该研究可获取耕作设备切削阻力,但没有考虑到不同设备会产生不同阻力,导致该模型使用范围受到限制;丁启朔[2]等人提出基于田间摄像的深松扰动行为和效应研究。利用土壤耕作原位综合测试系统完成深松实验,从五个不同方位录制深松视频,通过视频分析土壤紧实度与失效机理以及深松效应影响。但是由于该方法模型的实验成本较高,导致该模型无法广泛应用。
为此,本文利用SPH方法构建深松铲破坏土壤仿真模型。SPH方法属于拉格朗日算法[3],是解决高度非线性问题的有效方式。将此方法与有限元(Finite element method,FEM)相结合,最大程度体现出两种算法优势,更加精准地实现深松铲破坏土壤过程仿真。
2 深松耕作模型构建
在深松耕作时,梨底层被间隔式破坏,生成相间存在的构造,此种构造能够缓解土壤退化现象,有助于土壤保持肥力。还能提高气体交换能力,确保土壤充分吸收养分,使农作物增产。深松铲对土壤的破坏原理如图1所示。

图1 深松铲破坏原理示意图
可将整个切削过程当作土壤受到外界作用力被划分成不同形状的过程。有关研究表明,入土深度不同土壤的失效方式也不同[5]。
田地可当作没有边界的土壤,但受到仿真模型限制,无法建立较大的土壤模型。本文建立的土壤模型长宽高分别表示为0.5m、0.3m、1.5m。结合有关约束条件仿真实际状况,利用SPH方法分析深松铲破坏土壤的过程。
3 基于耦合分析的深松铲破坏土壤仿真模型
3.1 SPH+FEM耦合分析模型
SPH的基础方程为守恒方程[6],能够有效解决大变形问题,适用于分析土壤变形破坏等非线性问题。差值理论是SPH的根本理论,利用差值函数描述全部质点发生的相互作用,获取某点估计值,将守恒定律变换为积分形式,完成转换求和。
在SPH算法中,质点近似函数公式如下

(1)
式中,W代表核函数,h表示光滑长度,该值随时间与空间的变化而变化。
将核函数W通过辅助函数θ表示,获取尖峰函数W(x,h)

(2)
式中,d代表空间维数。
该算法中普遍使用的光滑核表示为

(3)
式中,C为常量,取决于空间维数多少。u为光滑核系数。
h的不断变化会对仿真精度产生重要影响,它可以确保存在足够多的质点,使质点连续有效。若h为固定值,容易出现数值畸变现象,光滑长度的最佳变化范围规定为
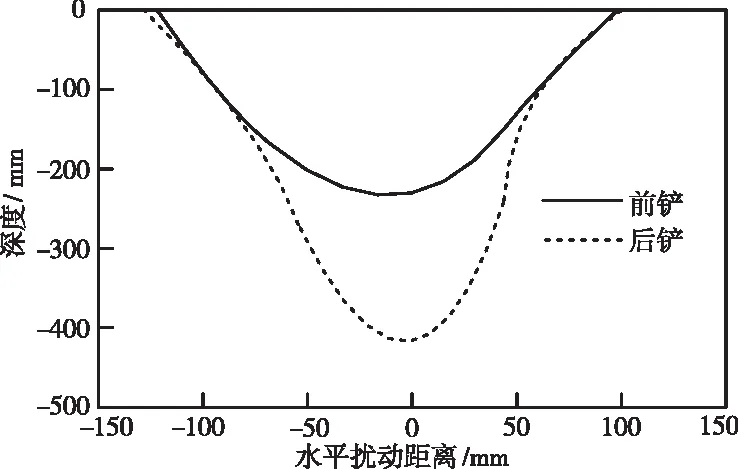
C1·h0 (4) 式中,h0代表原始光滑长度,C1与C2表示缩放因子。且C1=C2,h值始终不变。但是SPH算法在边缘约束处理方面还需改进,本文将SPH与FEM相结合,当变形区域较大时利用SPH方法,如果变形区域较小则利用FEM方法,确保两种算法发挥出最大优势,提高仿真模型精度。 图2代表两种算法的耦合模型示意图。上部分为SPH质点,下侧区域是FEM网格。利用惩罚函数达到两个区域力学参数传递的目的。网格边界部分与SPH质点相互接触,采用点-面形式完成耦合。 图2 耦合结构示意图 耦合算法下,粒子密度若比单元密度大,则表明仿真精度较高。为提高仿真模型精度,将0.2倍与2.0粒子间距分别当作光滑长度极小、极大值。 因此失效准则[7]可定义为 (5) 式中,fn与fs分别代表法向力与剪切力,fn,fail与fs,fail分别表示法向与剪切力指数。 3.2.1 深松铲受力分析 利用上述构建的耦合模型分析深松铲作业时,产生的阻力情况。 1)铲尖和铲柄同时破坏土壤 深松铲通常为平移前进,铲尖破坏土壤时会产生土壤耕作阻力。因为铲尖与土壤之间存在的深度较大,所以前进过程中受到的力来自土壤垂直方向。铲柄在作业时会受到土壤水平方向的耕作阻力,假设两种阻力分别表示为k1与k2,铲尖与铲柄的长度通过l1、l2描述,则同时生成的阻力F1的计算公式如下 F1=k1l1+k2l2 (6) 2)刀面破坏土壤 深松铲工作时,刀面对土壤产生挤压作用,土壤与刀面之间的力包括法向压力FN与摩擦阻力Ff=μFN,这两种力在水平方向中的投影为阻力F2 F2=FNsinα+Ffcosα=FN(sinα+μcosα) (7) 式中,α代表深松铲入土角度,μ为深松铲和土壤之间的摩擦系数[8]。 已有研究显示,当耕地深度在400-500mm区间内,土壤的正向压力情况近似表示为δ0=90kN/m2,因此土壤的正向压力[9]计算公式如下 δ=ξδ0 (8) 式中,ξ代表土壤有关系数。 假定深松铲的工作区域面积表示为S,法向压力FN的计算公式如下 FN=Sξδ0 (9) 则得出法相压力FN与摩擦阻力Ff存在如下三角函数关系 Ff=FNtanφ=μFN (10) 式中,φ代表土壤内摩擦角。 将式(9)与式(10)代入到式(7)中,重新获得刀面破坏土壤生成的阻力F2的计算公式 F2=Sξδ0(sinα+tanφcosα) (11) 3.2.2 深松铲对土壤的破坏过程 获取深松铲与土壤之间的摩擦力后,对深松铲破坏土壤的过程完成仿真建模。破坏过程可分为前铲对土壤的切削与破碎、后铲对土壤的切削与破碎两个阶段。 1)前铲破坏过程 前铲的入土深度小,先与土壤发生接触,如果铲尖表层光滑,没有磨损,这时铲尖作用在无限大土体上,形成作用力P及夹角α。在此过程中,土壤受到的压缩力σr呈现径向分布,而垂直方向上表现为自重应力σsz。 土壤产生的抗剪性能持续增大,当出现最大值,铲尖对土壤生成削切作用,整个土块失效破坏。发生形变的土块变换成有限体积,这时仅受到来自没有失效土壤的作用力[10]。 前铲逐渐前行,铲尖使部分土壤提升。在持续作用力下导致上升的土壤与土体之间形成作用应力。在不同力的相互作用下,升起的土壤表层与内部出现褶皱现象,生成拉伸应力。又在自重力作用下土壤中方向发生破碎。 2)后铲破坏过程 由于前铲先行作用于土壤,促使后铲作业区域土体自重应力下降。当不存在浅层土壤影响下,后铲可以提升土壤,确保深松深度,优化疏松效果。 3)土壤扰动体积 明确深松铲前、后铲的破坏过程后,分析土壤扰动效果。在综合分析深松环境下土壤的不同方向破坏差异,构建土壤破坏模型。为便于定量研究,假设破坏滑移面的螺旋线为直线,并将土壤扰动体积表示为V1。 因前、后铲土壤破裂线完全吻合,则两铲的土壤破坏半径表示为 Rr=d(cotα+cotβ) (12) Rf=df(cotα+cotβ) (13) 式中,Rr与Rf分别代表前后铲土壤破坏半径,d与df分别描述前铲与后铲的入土深度。 前铲和后铲的间距计算公式如下 Xsp=Rr-Rf=(dr-df)(cotα+cotβ) (14) 分析上述公式能够得出,如果前铲和后铲的间距发生改变,则土壤抬升体积随之改变。假设前铲可抬升的土壤体积记为V11,两铲之间松动的土壤体积为V12,后铲作用力下提升的土壤体积设置为V13,它们的表达式分别如下所示 (15) V12=dfXspW (16) (17) 前铲与后铲提升土壤体积V1表示为 (18) 分别分析前后铲对土壤的破坏过程,计算出两铲对土壤的破坏半径与土壤抬升体积,完成深松铲破坏土壤仿真模型构建。 为证明本文仿真模型的可行性,选取某地区的紫色土壤进行仿真。土壤的相关参数如表1所示。 表1 仿真目标参数表 构建SPH土壤模型,土壤形状为550mm×650mm×500mm。每个方向的粒子层数设置为60、40与45。深松铲的相关参数如表2所示。 表2 深松铲相关参数表 为利用本文方法构建的仿真模型对深松铲破坏土壤的轮廓状况进行分析,分别获得深松操作后土壤区域内前铲与后铲对土壤的宏观破坏轮廓。绘制为横向破坏轮廓,计算轮廓宽度。当深松铲入土深度分别为50mm、100mm、150mm、200mm时,前后铲对土壤的破坏轮廓分别如图3-6所示。(图中,深度表示深松作业完成后,沟底与未耕地表之间的垂直距离。) 由图3-图6可知,当入土深度不断变化时,土壤破坏轮廓存在较大差异。随着深度增加,破坏轮廓的平均宽度随之扩大,土壤扰动范围也持续增加;前后铲之间的土壤深度减小。结合该仿真结果,若要想改变土壤破坏体积,需在变化入土深度的同时调整前铲与后铲之间距离。 图3 入土深度为50mm时土壤破坏轮廓 图4 入土深度为100mm时土壤破坏轮廓 图5 入土深度为150mm时土壤破坏轮廓 图6 入土深度为200mm时土壤破坏轮廓 (19) (20) (21) Uj=1-Vj (22) 表3 不同入土深度的指标变化表 由表3可知,当前铲的入土深度为100mm时,标准差、变异系数最小,稳定系数最高。这表明100mm是最佳入土深度,此时深松稳定性较强。这是因为土壤自身属于非均质的,且自重应力会随着入土深度的加深而提高,当超过100mm时,铲尖容易与坚硬石块发生碰撞,因不能有效克服石块的自重应力,深松铲会向上弹起,造成波动较大,降低稳定性。 经过上述仿真,获取了入土深度对土壤破坏轮廓的影响规律,并确定最佳入土深度,为提高深松操作性能提供理论依据。 土壤介质具有复杂、高度非线性等特征,本文将光滑粒子流体动力学与有限元算法相结合,构建深松铲破坏土壤的仿真模型。通过该模型能够得出随着入土深度的加深,土壤破坏轮廓逐渐增大,同时确定了最佳入土深度。 但是本次仿真利用的土壤属于原状土,内部的某些因素可能对土壤性质造成影响,导致实验存在一定误差。在今后研究中,需对土壤样本做预处理,确定所有因素对指标产生的影响,使获得的结果误差更小。

3.2 深松铲破坏土壤仿真模型构建
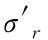



4 仿真设计与结果分析





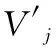



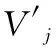

5 结论

