污水处理曝气系统优化控制仿真研究

孙宏存,于广平,李 崇,刘 坚

(1. 沈阳化工大学信息工程学院,辽宁 沈阳 110142;2. 广州中国科学院沈阳自动化研究所分所,广东 广州 511458)

1 引言

污水处理中的活性污泥法是一种污水生化处理方法,曝气系统是极其重要的控制部分￣[1],主要是向污水处理的好氧池中通入氧气,曝气量直接影响污水中溶解氧的浓度,从而影响出水水质的好坏,污水处理系统具有耦合性强[2],大滞后等特性[3],精准曝气一直以来都是污水处理过程中的一个难点,魏伟等针对溶解氧的控制,设计了一种有限时间自抗扰控制,来解决污水处理过程中的不确定性,对溶解氧调控取得一定效果[4]。栗三一等提出污水处理决策优化控制方法,对出水氨氮和出水总氮峰值进行抑制并降低能耗[5]。项雷军等提出了自适应补偿能力的输出反馈预测控制系统,当溶解氧浓度测量不准确时可通过反馈系统进行补偿调整[6]。周红标针对污水处理过程提出了基于自组织模糊神经网络的控制方法,在实际工况的动态变化下,溶解氧浓度的设定值可以被精确的跟踪,有着稳定的控制[7]。乔俊飞等提出一种基于知识的优化控制方法,采用记忆多目标优化算法构建环境变量参数与最优解之间的知识模型,算法的收敛性提高以获取更高质量的解[8]。

以上研究对污水处理溶解氧浓度的设定值优化和跟踪控制都取得显著的成效,但是未考虑污泥状态及出水的平稳性等问题,对设定值优化未形成闭环的反馈系统,针对这一问题本文在建立预测模型时考虑多因素影响,设定值优化后设计评估反馈系统,不断更新模型参数,使溶解氧设定值趋于最优。

2 污水处理曝气过程优化

污水处理曝气过程优化是通过优化目标函数产生优化设定值,采用BSM1仿真平台进行仿真[9],评估出水水质,对系统进行反馈。主要包括建立基于BP神经网络[10-12]的能耗和出水水质模型;研究关于能耗和出水水质的多目标优化方法[13,14];建立对于复杂入水工况的识别[15]、出水评估反馈系统。

首先根据BSM1模型提供的三类历史数据,通过搭建的simulink模型对三类数据进行仿真,采用BP神经网络分别以入水流量、组分、溶解氧设定值与能耗和出水氨氮建立两个模型。以能耗最小为优化目标,以出水氨氮值作为约束条件。用粒子群算法寻找出该数据对应的最优溶解氧设定值。将每一类入水工况与溶解氧设定值存入工况库中。对于新的输入数据通过高斯混合模型[16]与已有类别进行比较,通过欧氏距离匹配得到相应的操作参数。若经高斯混合模型比较相似度未达预设阈值,则将该组数据作为新的一类,仿真、寻优得到溶解氧设定值,最后用该设定值通过仿真平台验证,评估出水水质指标对模型数据库进行更新。系统框图如图1所示。

图1 系统框图

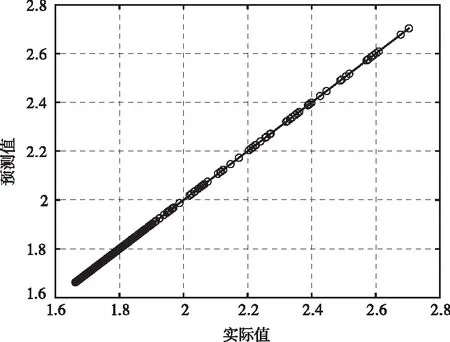
图2 氨氮值预测模型效果图

2.1 BP神经网络能耗和出水水质模型

考虑到污水处理过程出水水质指标和操作变量之间关系具有强非线性、不确定性、机理不清的特点,通过机理建模来预测出水水质的指标难以保证其模型的准确性可靠性。因此引入能耗和出水水质模型代替污水处理系统对能耗和水质的计算。

BP 神经网络是一种基于误差反向传播算法训练的多层感知器前馈网络,不需要了解输入与输出之间的关系。模型通过简单的非线性函数多次拟合后,实现高维度非线性的精确映射[17],具有较强的自适应能力,根据活性污泥1号模型(ASM1)提供的三类历史数据,本文采用BP神经网络分别以入水流量13种入水组分及曝气池3、4、5池溶解氧设定值为输入,出水能耗和出水氨氮为输出建立两个预测模型。采用Trainlm函数、Levenberg-Marquardt算法、隐含层2层15-20、激活函数tansig、函数训练次数1000、学习效率0.01、收敛误差1e-7。

氨氮值预测结果如2所示,mse=2.48*10-8,能耗预测结果如图3所示,mse=1.4*10-3。

图3 能耗预测模型效果图

2.2 溶解氧设定值优化

一般粒子群算法是通过模拟鸟群觅食行为的一种全局优化进化算法,该算法在计算过程中保留了最优全局位置和粒子已知的最优位置两个信息[18]。对较快收敛速度以及避免过早陷入局部最优解产生了不错的效果。在各个领域得到了广泛的应用[19,20]。

本文在标准的粒子群算法的基础引入了惯性因子,在算法的收敛性能有了很大的改善,在PSO算法中,在一个目标搜索范围为D维的空间中,初始化M个粒子,组成一个种群T={X1,X2,…,XM}Xi=(xi1,xi2,…,xiD),i=1,2,…,M,表示第i个粒子在D维空间的位置,vi=(vi1,vi2,…,viD),i=1,2,…,M,表示第i个粒子的速度。第i个粒子到目前为止所搜索到的个体极值表示为Pi=(Pi1,Pi2,…,PiD),i=1,2,…,M,在整个粒子群中,所有粒子到目前为止所搜索到的全局极值表示为Pg=(Pg1,Pg2,…,PgD),g∈{1,2,…,M}。每个粒子代表一组溶解氧的设定值(DOset),粒子每更新一次适应度就随之更新一次,在此过程中适应度值是由入水数据和粒子对应的DOset通过能耗模型计算出能耗,由于出水水质中有机物浓度越接近约束的最大值,污水处理过程能耗越低,且出水水质中氨氮值最容易超标,因此利用入水数据和粒子对应的DOset通过氨氮模型计算出的出水氨氮值作为约束值。则第i个粒子就是按照下面的式(1)和(2)来更新自己的速度和位置。

(1)

(2)

式中,i=1,2,…,M,M是群体中的粒子数;K是迭代次数;c1和c2为学习因子,r1,r2是均匀分布于[0,1]之间的两个随机数。ω为惯性因子。取晴天雨天暴雨天各4天,采样时间为15分钟共1152条数据进行溶解氧设定值寻优,粒子群相关参数:种群个体数60、迭代次数1000、惯性因子0.5～0.8、学习因子0.5,图4、图5、图6分别为晴天、雨天、暴雨天三个好氧池优化后的溶解氧设定值。

图4 晴天溶解氧设定值

图5 晴天溶解氧设定值

图6 晴天溶解氧设定值

2.3 评估反馈系统

评估反馈系统包括入水工况识别和数据库更新,入水数据通过高斯混合模型进行分类,采用欧氏距离进行入水工况匹配,结合Benchmark的污水处理仿真平台BSM1对数据进行仿真验证,通过对比仿真结果与出水水质标准进行数据库更新。评估反馈系统框图如图7所示。

图7 评估反馈框图

图中新工况A表示一组新的入水数据,其中参考变量包括入水的流量和13种组分,历史工况库1、2、3分别存放着晴天雨天暴雨天三类入水流量组分及每个池子的溶解氧浓度,d1、d2、d3为高斯混合模型所计算的概率,a为阈值(95%),操作变量为各个池子的溶解氧设定值。

混合高斯模型的数学模型为式(3)

(3)

分类后计算当前入水工况与该历史工况库中的各工况之间的相似度。采用欧氏距离进行相似度计算记当前工况为T=(t1,…,ti,…tn),其中ti是第i个输入属性的归一化特征值,Xk为历史工况库第k条入水工况,计算T与Xk的相似度如式(4)所示

(4)

k=1,2,…,p通过计算比较p个相似度,分别为S1,…,Sp,选相似度最高的一组,读取操作参数。

本文的评估标准是采用Benchmark基准给出的出水水质指标(EQ)及曝气能耗(AE)。

出水水质指标计算如式(5)所示:

(5)

曝气能耗计算如式(6)所示:

(6)

SS,COD,SNKj,e,SNO,e,BOD5,e为5种出水指标,Qa、Qr、Qw分别表示内回流流量、外回流流量、污泥排放量;Kla为氧转移速率,表征好氧池的曝气情况;T=4days,Qe为出水流量。

3 仿真验证

为了更加有效地模拟和评估污水处理过程曝气过程中使用的控制和优化策略,本文采用仿真基准模型 1号进行验证,BSM1 主要由生化反应池和二次沉淀池构成,生化反应池共有5个模块,2个厌氧区,主要进行反硝化反应,3个好氧区,主要进行硝化反应。配合内外回流,保证了曝气池中固体悬浮物的浓度,维持了活性污泥系统的稳定性。取晴天雨天暴雨天各四天,采样时间为15分钟共1152条数据作为验证数据,当入水数据进入系统后,通过优化得到得溶解氧设定值(下文统称优化后)与BSM1的原系统(下文统称优化前)Kla3=Kla4=10h-1,DO5set=2mg/L仿真结果进行比较。BSM1系统框图如下图8所示。

图8 BSM1系统图

优化前后出水水质对比图如图9、图10、图11、图12所示。

图9 出水氨氮浓度对比图

图10 出水COD浓度对比图

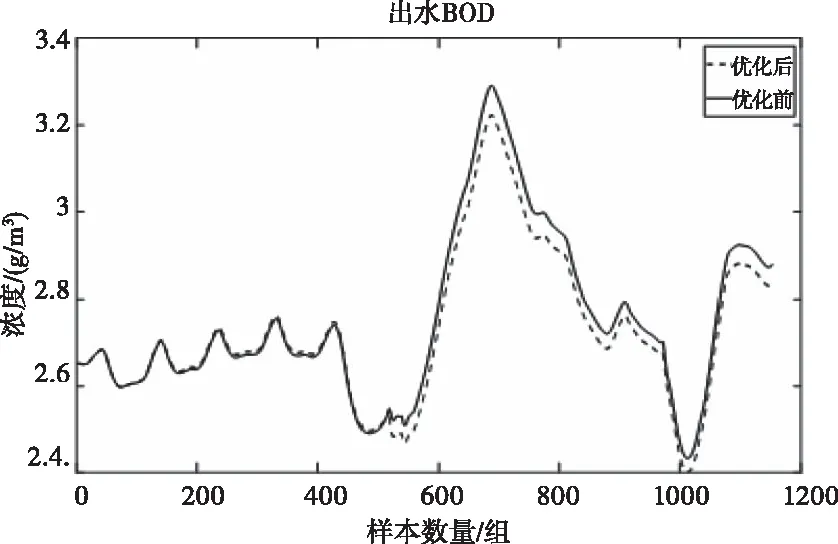
图11 出水BOD浓度对比图

图12 出水总氮浓度对比图

出水水质各指标如表1所示。

表1 两系统出水水质

两系统的曝气性能指标如表2所示。

表2 两系统污水处理性能

由图表信息可知经优化后晴天在出水水质降低2%的同时风机能耗降低18%左右,雨天在水质降低1%风机能耗上升不到3%,暴雨天在水质稍有上升的情况下风机能耗降低4%。

4 结语

与传统的污水处理曝气过程溶解氧控制相比,基于数据驱动的优化控制方法在复杂多变的入水工况下可以更精准的控制溶解氧的浓度。该方法具有以下特点:1)采用BP神经网络建立预测模型,考虑综合因素的干扰,非线性预测能力强,鲁棒性好,可快速预测出水。2)粒子群优化算法,算法精度高,收敛速度快,避免算法停滞现象。3)具有评估反馈系统有不断更新模型能力,使结果精度更高。最终经验证与原始数据对比得出,在出水水质变化不大的情况下总能耗降低了7%左右。