基于平滑S形曲线的永磁球形电机轨迹规划

骆成路,王群京,4,武思傲,李国丽

(1. 安徽大学电气工程与自动化学院,安徽 合肥 230601;2. 高节能电机及控制技术国家地方联合实验室,安徽 合肥 230601;3. 工业节电与用电安全安徽省重点实验室,安徽 合肥 230601;4. 工业节电与电能质量控制安徽省级协同创新中心,安徽 合肥230601)

1 引言

永磁球形电机是一种能够实现三自由度运动的电磁执行装置,它因具有体积小、精度高、结构新颖的优点而备受诸多领域所关注[1-3]。

在球形电机轨迹规划领域,天津理工大学的吴凤英等人利用不同算法针对转子在给定轨迹下的最短运行时间和加速度冲击做了运动学上的优化[4,5],但是其提出的算法并未考虑电机转子体动力学因素对其运行轨迹造成的影响。安徽大学的李绅采用三次样条插值的方法实现了球形电机的连续轨迹规划,并利用基于正弦加速度的点对点规划算法推导出对应的通电控制策略[6],但该策略并未考虑转子运行时的速度特性。Cheon H, Wang L等人研究了多自由度机器人与机械臂在三维空间中的轨迹规划算法[7,8],为球形电机的轨迹规划提供了一定理论基础。

S形曲线的轨迹规划算法最早应用在数控机床的控制中,该算法最显著的特点是对应的加减速曲线形如字母S形的走势,平滑的速度规划方式使得系统在运行时更加具有柔性,但其阶跃变化的加加速度仍然会对系统造成一定的冲击,从而引起机床的振动影响控制精度[9]。在S形曲线的应用领域,Chen Qizhi,Zhe Liu等人推导了S形曲线的加减速原理,利用S形曲线平滑连续的特性实现了其在数控系统领域中的高精度控制[10,11]。Fang, Yi和Fang, SX利用分段连续的加加速度算法改进了S形加减速曲线,进而提高了工业机器人在运行过程中的柔性[12,13],为改进S形曲线在球形电机中的应用提供了理论依据。

本文提出了的轨迹规划方法创新点在于,将S形曲线与球形电机转子动力学模型结合,相比与文献[4,5],实现了其在球形电机动力学层面上的应用;利用正弦函数无限可导的特点拟合改进S形曲线,相比与文献[9],使球形电机输出速度呈现S形的平滑加减速趋势,提高了球形电机在运行时的稳定性。

2 永磁球形电机的结构与控制转矩描述

2.1 永磁球形电机的结构

本文所研究的球形电机具体结构如图1所示[14],该电机本体主要由定子和球状转子组成,其中定子线圈结构分布为2/24方式,即上下两层定子外壳各内嵌12个线圈,由12块驱动电路板单独供电;转子体上永磁体分布为4/40方式,且永磁体由钕铁硼材料加工而成,二者交替排列于转子体上。当不同序列线圈通电后,线圈产生的磁场与永磁体的磁场相互作用产生不同方向的控制转矩,驱动转子实现三自由度运动。

图1 永磁球形电机本体结构图

2.2 永磁球形电机的动力学模型

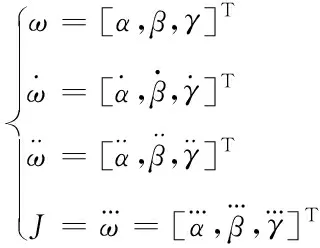
(1)

由刚体坐标变换原理与拉格朗日第二方程可得球形电机的动力学方程为

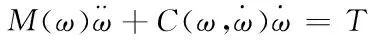
(2)

(3)

其中Jx,Jy,Jz是转子体在X、Y、Z轴方向上的转动惯量,将转子模型导入ADAMS软件中经计算其三轴转动惯量满足

(4)

于是离心和哥氏力项可表示为

(5)

2.3 基于坐标分解的永磁球形电机控制转矩描述

根据刚体在空间中的坐标变换原理,本文采用XYZ的坐标旋转次序描述球形电机末端位置的姿态角,即在三维坐标空间中转子输出轴末端A点在运动约束范围内任意旋转φ角到B点都可以视为其先绕X轴旋转α角度到A1(YOZ平面内),再绕Y轴旋转β角度到A2(XOZ平面内),最后再绕Z轴旋转γ角度到B点(XOY平面内)。具体旋转角φ的分解如图2所示。且令A的坐标为(xA,yA,zA),B的坐标为(xB,yB,zB),R为球心到输出轴末端的距离(本电机中R=105mm)。

图2 旋转角φ的坐标分解

经过三次坐标旋转变换,并通过转子末端姿态的逆运动学求解,即可得到输出轴末端空间直角坐标与对应欧拉旋转角之间的关系为

(6)

此坐标分解方法有利于求解球形电机的控制转矩,具体分析如下。当转子绕X轴由A点旋转至A1点时,此时旋转角β与γ及其角速度、角加速度均为零,则有

(7)

将其带入式(2),可得X轴方向上的控制转矩为

(8)

同理可求出输出轴末端由A1旋转至A2,由A2旋转至B时的控制转矩分别为

Ty=TA1-A2=[0,J*,0]T

(9)

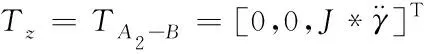
(10)

因此由式(8)、(9)、(10)可知,对球形电机轨迹规划的问题可视为对已知运行路径的加速度进行规划。

3 平滑S形曲线的永磁球形电机轨迹规划

3.1 S形曲线的运动学特性及规划策略设计

S形加减速曲线的由来是因为电机在加减速阶段的速度曲线呈现为S形,典型S形曲线在运行过程中分为7段:加加速段(I)、均加速段(II)、减加速段(III)、匀速段(IV)、加减速段(V)、匀减速段(VI)和减减速段(VII)。现给出7段S形曲线的加速度方程

(11)

(12)

再次积分得到完整S形曲线对应的角位移:

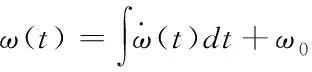
(13)

针对球形电机的控制转矩描述,设计适用于其动力学方程的速度规划策略为:

1) 转子启停时刻速度均为零,即加速阶段速度由0加速到最大值曲线呈现为S形,减速阶段由最大值减速到0亦为S形;

2) 为最大程度减小控制转矩的不对称性对系统造成的影响,令每个阶段的加减速持续时长相等;

3) 由式(10)可知,加速度为0时控制转矩也为零,因此对球形电机的动力学规划不考虑匀速阶段。

考虑上述约束,设一个规划周期的时长为T,总角位移为ω,则在该规划策略约束下的S形曲线对应的加速度方程为

(14)

将式(14)带入转子动力学方程,即可得到角位移ω与规划周期T约束下的三轴控制转矩。

3.2 正弦函数拟合改进S形速度曲线

对式(11)求导可得S形曲线的加加速度方程,经分析该规划方式下加加速度的值一直在Jmax,0,-Jmax之间呈阶跃形变化,当系统加减速形式发生转变时,此形状的加加速度会对系统产生冲击,使得系统不具有柔性,这在高精度控制系统中是不被允许的[15]。正弦函数本身具有无限可导的特点,若将其用于拟合改进原S形曲线的速度参数,则不仅使得转子输出角速度仍然为S形,且经过二次求导后的加加速度仍然可导,即不仅消除了加加速度的阶跃现象,而且使得系统能够更加稳定的运行。设拟合S形速度曲线的多阶正弦函数为

(15)

其中ai,bi,ci为待求拟合参数,为防止过拟合现象,设拟合阶数为j(j=1,2,3)。

现根据式(14)设计输出轴末端由原始点在5秒内沿X轴逆时针旋转20度的动力学方案,以确定适用于改进S形曲线的拟合阶数,进而规划更为复杂的轨迹。将运动过程中的角速度与时间的信息提取并进行拟合得到各阶拟合曲线及拟合误差曲线如图3、图4所示。其中图4中的Errorj2与Errorj3分别为j=2与j=3时的拟合数据与源数据的差值。

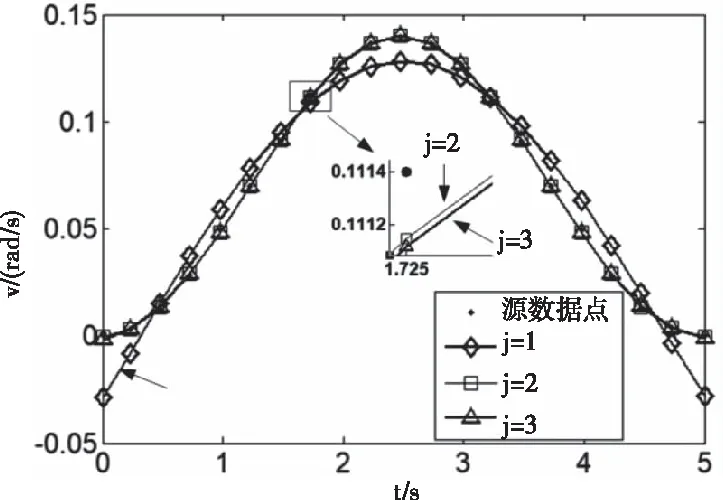
图3 多阶正弦函数拟合曲线图

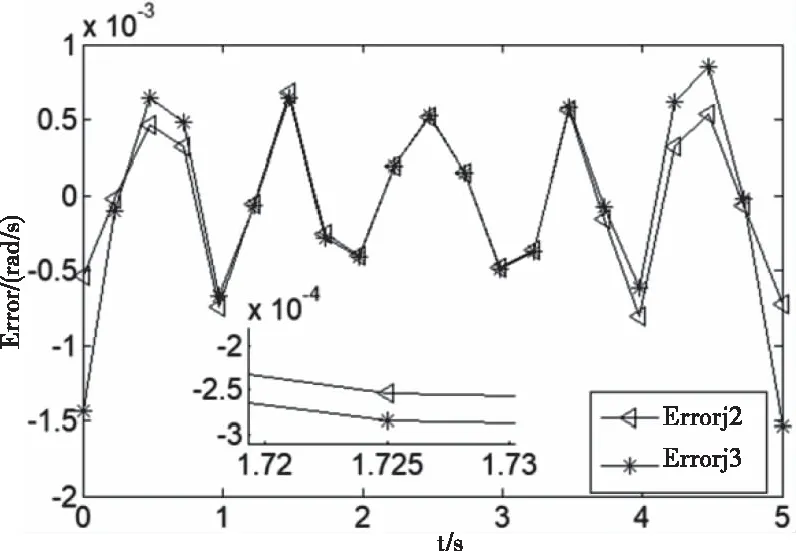
图4 拟合误差曲线图

由图3可知,j为1时对应的拟合速度曲线不满足S形的加减速趋势,j为2,3时虽已经达到S形的加减速效果,然而对比图4可知,j为3时的最大拟合误差较j为2时的大,且总体趋势不如j=2时的误差波动范围小。于是选择j为2时的拟合阶数,作为改进后的速度规划方式,结合式(15),改进后的角速度输入信号为

(16)

对式(16)求导可得对应的加速度方程

(17)

将式(17)带入球形电机动力学方程即可求出改进后各旋转角所对应的控制转矩。

4 动力学仿真验证

本文仿真验证平台选用ADAMS动力学仿真软件,首先将转子体模型以一定格式导入ADAMS/VIEW模块进行可视化仿真,观察规划路径;其次在Post-processing 后处理模块导出转子输出角速度、角加加速度数据并进行分析。现给定球形电机末端关键点位置信息如表1所示,旋转次序为A-B-C-D。

表1 关键点空间直角坐标信息

将上述关键点之间的欧拉旋转角求解出后,设每两点之间运行时间为2s,总时长为6s。经式(14)、(17)可求出改进前后轨迹规划策略所对应的加速度方程,进而得到两种方式的控制转矩如图5所示。其中S-TX、S-TY、S-TZ与SinS-TX、SinS-TY、SinS-TZ分别表示改进前与经正弦函数拟合改进后转子体在X、Y、Z轴方向上的控制转矩。

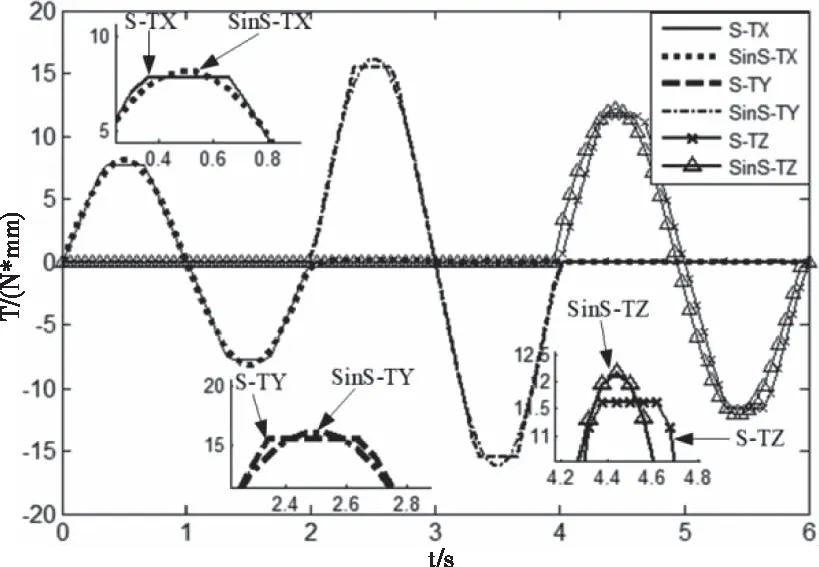
图5 两种方式的控制转矩图

由上图可以看出,原S形曲线对应的控制转矩为梯形,因此在转子加减速切换时刻会有转矩拐点的出现,不利于系统的流畅运行。然而经过改进后的转矩曲线可以看出,二阶正弦函数的改进方式平滑了原曲线的拐点,有利于转子加减速方式的平滑切换。将上图中的控制转矩输入至ADAMS软件建立的永磁球形电机转子动力学虚拟样机中,得到表1对应的仿真轨迹曲线如图6所示。

图6 动力学仿真轨迹

为进一步分析改进前后转子末端的速度特性,经ADAMS后处理模块导出该轨迹的速度曲线如图7所示,图中S-VX、S-VY、S-VZ与SinS-VX、SinS-VY、SinS-VZ分别表示改进前与经正弦函数拟合改进后转子体在X、Y、Z轴方向上的输出角速度。

图7 输出轴末端角速度曲线

可以看出在每2s的规划周期内,无论是改进前还是改进后,输出轴末端速度在加速和减速阶段均呈现为S形的趋势,且运行过程符合本文所设计的速度规划策略。再者由于本文采用二阶正弦拟合的方式改进原S形曲线,由图7知,改进后速度曲线与原S形曲线几近重合,说明拟合改进的结果是正确的。为进一步体现改进后的方式对转子运行过程中冲击的优化,现导出转子末端加加速度曲线如图8所示,其中S-JX、S-JY、S-JZ与SinS-JX、SinS-JY、SinS-JZ分别表示原S形曲线与经正弦函数拟合改进后转子体在X、Y、Z轴方向上的输出角加加速度。

图8 输出轴末端角加加速度曲线

角加加速度反映了系统的冲击特性,在图7的每个规划周期内,原S形曲线对应的阶跃形状的加加速度被改进后的速度规划策略所优化,使得转子体在运行过程中更加具有柔性,保证了球形电机的平稳运行。此外考虑到刚体的建模误差与改进算法的拟合误差,设ErrorX、ErrorY、ErrorZ分别为转子体在X、Y、Z轴方向上的角位移仿真数据与理论数据的差值,记为角位移误差(Error),经计算分析其误差曲线如图9所示。

图9 输出轴末端角位移误差曲线

由图9可知即使存在建模误差与拟合误差,然而在整个规划周期内,第5秒时达到的最大误差也不足0.01rad,说明了本文提出改进算法的可行性。

5 结论

本文提出了一种基于平滑S形速度曲线的永磁球形电机轨迹规划方法,在控制转矩、角速度、角加加速度和角位移误差四个方面进行改进前后轨迹规划的仿真分析,可以得到以下结论:

1) 利用二阶正弦函数改进后轨迹规划算法获得了较为平滑的控制转矩和加减速度曲线。实现了速度的平滑输出。

2) 解决了原S形速度曲线存在的加加速度阶跃现象的问题,减小了对系统造成的冲击。

3) 通过误差分析得到误差控制在0.01rad以下,证明了此算法的可行性。

通过对特定轨迹的仿真分析,验证了本文所提出轨迹规划方案的有效性与优越性,为球形电机的高精度控制奠定了基础。