基于多目标问题的装备维修保障资源调度研究 *

祝东攀，曹继平，毕杰

（火箭军工程大学，陕西 西安 710025）

0 引言

信息化条件下的战争具有突发性强、作战节奏快、战场形势变化迅速等特点，这些特点势必导致装备维修保障任务越来越重。战时，时间是赢得战争的关键因素，如何使受损装备尽可能快地恢复战斗力，再次投入战场，主要是由装备维修保障水平决定的，因此，提高装备维修保障能力是取得战争胜利的前提和基础。维修保障资源是装备维修保障能力的重要支撑［1］，装备维修保障水平的高低，一定程度上跟维修保障资源能否满足武器装备的维修保障需求有关。装备维修保障资源调度，是指在装备维修保障工作中，对维修保障所需要的各类保障资源进行合理分配［2］，因此研究装备维修保障资源调度问题对提高战时部队装备维修保障能力具有重要意义。

资源调度问题相关理论研究背景涉及物流、消防、军事和应急保障等领域。李悦等［3］研究了基于物联网平台下铁路物流中心装卸资源的调度优化问题，构建了以平均延误时间最短和最大作业时间最小为目标的多目标调度优化模型，对提高铁路物流中心的装卸效率具有一定意义。吴鹏等［4］针对资源受限情况下森林火灾救援的问题，在根据火灾严重程度和火势蔓延速度对火灾救援优先级划分的基础上，构建了以救援时间最小为目标的消防救援车辆路径优化的线性规划模型，为解决资源受限下森林火灾资源调度问题提供了一种解决办法。宋卫星等［5］针对装备维修保障任务量大、保障资源有限的问题，在分析装备维修资源投入与效益关系的基础上，构建了以维修装备数量最多、维修成本最低为目标的维修调度模型，对合理利用维修资源具有一定意义。李绍斌等［6］针对单需求点的战储资源调度问题，建立了以调度时间最少和调度成本最小的多目标调度模型，并运用模糊转换和线性规划的方法实现对模型的计算，为战时战储资源调度问题提供了一种解决思路。王薇等［7］针对高速公路交通事件应急救援问题，在分析高速公路施工区域对道路通行能力影响的基础上，以应急救援时间最短和应急救援相关费用最少为目标，构建了基于施工区通行能力的资源调度模型，为合理选择应急出救点提供了一种方法。陈超［8］、李沐鸿等［9］针对不确定条件下的应急资源调度问题，利用区间数完成了调度模型构建，为解决不确定条件下的资源调度问题提供了借鉴。这些理论研究均为战时装备维修保障资源调度问题研究提供了一定理论参考。但是，战时装备受损情况的不断变化导致维修保障资源需求不确定，维修保障资源在运输途中可能由于天气、自然灾害、敌特侵袭等原因，使得保障点到需求点运输时间不确定，道路、桥梁等交通设施遭敌打击后的通行情况不确定。上述研究大多是以时间、费用等单一因素为优化目标，且都假定保障资源的需求量和保障点到资源需求点的时间为确定值，具有一定局限性，没有体现出战时维修资源需求、维修资源配送时间等因素的不确定性，难以适应部队战时背景下时间紧、维修资源需求点多、维修保障点多等问题。装备维修保障活动是一项复杂的工程规划类活动［10］，对装备维修保障资源调度研究，若只针对某一单一目标进行优化，将会造成其他目标效益低下，不符合战时装备维修保障资源调度的情况。本文将构建不确定性多目标模型，引入三角模糊数来表示维修保障资源需求的不确定性、维修保障资源调度时间的不确定性、调度路径可靠性的不确定性，来制定最优的调度方案。

1 模型构建

1.1 问题分析

装备维修保障资源调度过程如图1 所示。战时，各作战单元根据任务部署在指定区域，当作战单元遭受敌打击或发生故障时，由伴随保障小组负责维修。如果伴随保障小组所携带的资源不足以完成维修任务时，作战单元指挥员将根据维修情况向指挥所申请调度维修资源。指挥所收到申请后，根据战前维修保障资源部署情况及作战单元受损情况制定调度方案，命令相应的维修保障点在规定的时间内将维修保障资源运送至所需要的作战单元。当部队本级维修资源不足时，向基地级维修保障力量申请支援，基地级维修力量收到申请后根据实际情况安排相应的维修力量和维修资源前往支援。

图1 装备维修保障资源调度流程图Fig. 1 Scheduling flow of equipment maintenance and support resources

战时装备多，分布地域广，装备维修保障资源呈现“多需求点，多保障点”特点，随着战争进程的变化，战场信息也处于不断变化当中。开展装备维修保障资源调度时，由于装备受打击情况、天气情况、道路和桥梁等交通设施遭敌打击情况等处于不断变化当中，因此维修保障资源的需求量、维修保障资源调度时间、调度路径的可靠性等无法确定。因此，以维修保障资源需求量、运输时间等因素为某一固定值处理战时装备维修保障资源调度方案难以客观反映实际。

1.2 不确定性装备维修保障资源调度

本文通过引入三角模糊数来表达战时维修保障资源需求的不确定性、维修保障资源调度时间的不确定性和调度路径可靠性的不确定性来建立合理的调度模型求解。维修保障资源需求点j对维修保障资源的需求量可表达为，这里三角模糊数为͂，模糊数的最保守估计值为xj1，模糊数的最可能估计值为xj2，模糊数的最乐观估计值为xj3；将维修保障点i向维修保障资源需求点j配送资源 的 时 间 表 示 为为 三 角 模 糊 函数，模糊数的最保守估计值为tij1，模糊数的最可能估计值为tij2，模糊数的乐观估计值为tij3；将维修保障点i到维修保障资源需求点j的路径可靠性表示为为 三 角 模 糊 函 数，模 糊 数 的最保守估计值为pij1，模糊数的最可能估计值为pij2，模糊数的最乐观估计值为pij3。

1.3 目标函数确定

战时，装备维修保障是为了让受损装备快速恢复战斗力，因此维修保障资源越能尽早到达需求点，维修保障分队就能越快对受损装备进行维修，故而装备维修保障资源调度的第一个目标便是维修保障资源调度时间最小。将以维修保障资源调度时间最小为目标的函数表示为

式中：xij为维修保障点i向维修保障资源需求点j提供的维修保障资源量为维修保障点i向维修保障资源需求点j配送维修保障资源所需的时间。

在进行装备维修保障资源调度时，从维修保障点将资源运送至维修保障资源需求点的路径可靠性问题也影响着维修保障的效率，合理的运输路径选择不仅能够将维修保障资源迅速、准确地运送至目的地，而且能够减少运输成本。装备维修保障资源调度的第二个目标便是维修资源顺利运输至需求点的路径可靠性最高。本文中假设相应的维修保障点到维修保障资源需求点的路径已经确定，只考虑该路径在战时遭受自然灾害和敌打击后可以快速修复、恢复通行的概率问题，如果概率越高，表示道路受损后恢复通行的速度越快，在运输过程中时间浪费越少，即路径可靠性越高。假定维修保障点i到维修保障资源需求点j的路径为Lij，该路径在战时遭受自然灾害和敌打击后可以快速修复，恢复通 行 的 概 率kij，则 令为 保 障 点i将 维 修 保障资源运送至需求点j的路径可靠性。

将以维修保障资源调度路径可靠性最高为目标的函数表示为

虽然战时装备维修保障以军事效益为主，但装备维修保障资源调度在满足时间最小和路径可靠性最高的条件下也应兼顾考虑调度成本问题，避免不合理的浪费。将以维修保障资源调度成本最小为目标的函数表示为

式中：cij为维修保障点i到维修保障资源需求点j的单位资源运输成本。

综上得到以装备维修保障资源调度时间最小、调度路径可靠性最高、调度成本最小的多目标函数可表示

2 约束条件函数的建立

假设各维修保障点的运力充足，现结合背景设置以下约束条件：

（1） 各维修保障点提供的维修保障资源总量与各维修保障资源需求点对资源的需求总量相等；

（2） 各维修保障点向维修保障资源需求点提供的资源量之和等于所有维修保障点实际供应量；

（3） 每个维修保障点所供应的维修保障资源量不大于其所储存的维修保障资源量；

（4） 维修保障资源调度路径的可靠性大于0；

（5） 维修保障点向维修保障资源需求点提供的维修保障资源量不小于0；

（6） 维修保障资源的需求量为三角模糊数；

（7） 维修保障资源配送时间为三角模糊数；

（8） 维修保障资源调度路径的可靠性为三角模糊数。

约束条件函数为

式（5）表示维修保障点提供的维修保障资源量与需求点对维修保障资源的需求量相等，其中：xij表示维修保障点i向维修资源需求点j所提供的维修保障资源量͂ 表示维修保障资源需求点j所需要的资源量。式（6）表示每个维修保障点向需求点提供的维修保障资源量之和等于所有维修保障点实际供应量；N表示所有维修保障点实际供应量。式（7）表示每个维修保障点所供应的维修保障资源量不大于其所储存的维修资源量；Ni'表示维修保障点所储存的维修保障资源量。式（8）表示维修保障资源调度路径的可靠性大于0。式（9）表示维修保障点向需求点提供的维修保障资源量不小于0。式（10）表示需求点j的维修保障资源需求量为三角模糊数。式（11）表示维修保障点i向需求点j配送资源的时间为三角模糊数。式（12）表示维修保障点i将维修保障资源运送至需求点j的路径可靠性为三角模糊数。

3 模型求解

3.1 算法分析

常用于解决多目标规划问题的方法有线性加权法、目标规划法、分层序列法、极大极小法、理想点法等［11］。本文模型采用极大极小法进行求解。由于多目标装备维修保障资源调度问题中，各目标函数的重要性不同，对调度问题的影响不同［12］，为避免某一单个目标函数主导整个目标函数优化过程，本文首先通过构造目标函数相对重要性判断矩阵，确定各目标函数的权重值；其次再通过求得各单目标函数的极大值和极小值，对目标函数进行规范化处理；最后将多目标函数转化为单目标函数，利用LINGO 软件进行求解。

3.2 算法求解过程

（1） 确定目标函数权重

邀请相关专家对各目标函数的重要性进行两两比较判断，并对指标因素的重要性程度按1-9 标度赋值［13］（表1 所示），构建目标函数的判断矩阵A。

表1 目标函数重要性判断标度Table 1 Judgment scale of objective function importance

由于判断矩阵的构造一定程度受专家的主观因素和个人判断能力影响，为检验判断矩阵的构造是否合理，还需对判断矩阵进行一致性检验［11］。根据一致性比例CR=CI/RI对各判断矩阵的一致性进行检验，其中一致性指标CI=λmaxn/（n-1），n为判断矩阵阶数，RI为平均一致性指标。当n=3 时，查得RI=0.58（见表2），若CR＜0.1，则认为构造的判断矩阵是合理的，否则需要不断校正。

表2 平均随机一致性指标RITable 2 Mean random consistency index RI

计算矩阵的特征向量W，wk（k=1，2，3）即为各目标函数的权重。

（2） 对目标函数进行规范化处理，即

式中：maxfk(x)和minfk(x)为目标函数可取值的极大值和极小值，k=1，2，3。

（3） 将多目标函数转化为单目标函数进行求解。

4 算例

某作战区域内战前共预置有3 个维修保障点，每个维修保障点储存的维修资源种类和数量如表3所示。假设在某次作战过程中因战场损伤导致参战的4 个作战单元装备受损，急需维修保障资源开展装备维修保障工作。由于战场环境处于不断变化当中，随着战争进程加深，以及天气等外界因素影响，作战单元受损装备数可能会不断增加，因此作战单元对维修保障资源的需求不确定，各维修保障点将维修保障资源运输至作战单元的时间不确定，维修资源运输路径可靠性不确定。通过有关部门评估，得到3 个作战单元对各类维修保障资源需求量的三角模糊数如表4 所示，维修保障点到各作战单元的单位资源运输成本、配送时间的三角模糊数和路径可靠性的三角模糊数如表5 所示，表内成本所对应的数据表示4 种资源中每种资源单位运输成本。现要求给出最优调度方案。

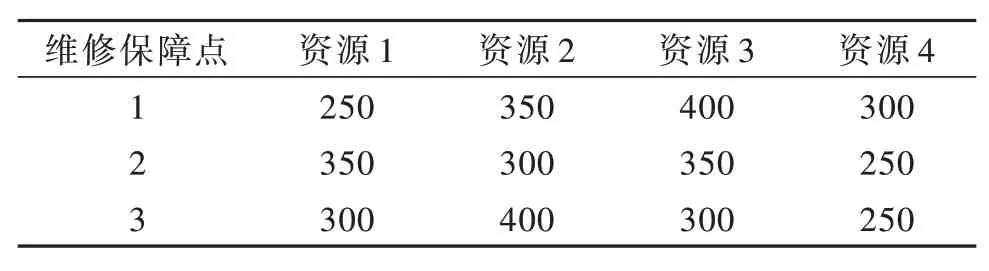
表3 各维修保障点储存的维修保障资源种类和数量Table 3 Types and quantities of maintenance and support resources stored at each maintenance and support point

表4 作战单元需要的维修保障资源种类和数量Table 4 Types and quantities of maintenance and support resources required for combat units

表5 维修保障点到各作战单元的单位资源运输成本、运输时间和路径可靠性Table 5 Transport cost， transport time， and transport path reliability of unit resource from maintenance and support point to each combat unit

已知此次作战任务中，指挥决策者是风险中立的，根据三角模糊数运算规则［14］，得到各类维修保障资源需求量的三角模糊数期望值如表6 所示，维修资源运输时间和维修资源安全送达受损装备处的概率的三角模糊数期望值如表7 所示。

表6 各作战单元需要的维修保障资源种类和数量的期望值Table 6 Expected types and quantities of maintenance and support resources required by each combat unit

表7 维修保障点到各作战单元的单位资源运输成本、运输时间和路径可靠性的期望值Table 7 Expected transport cost， transport time， and transport path reliability of unit resource from maintenance and support point to each combat unit

由以上数据，可建立资源1 以调度时间最小、调度路径可靠性最高、调度成本最小为目标的多目标调度模型：

（1） 首先邀请相关专家对各目标的重要性进行两两比较判断，并对指标因素的重要性程度按1-9标度赋值，得到目标函数的判断矩阵

根据一致性比例CR=CI/RI对判断矩阵的一致性进行检验，计算得CR=0.003 2，因为0.003 2＜0.1，所以认为该目标函数的判断矩阵是合理的。通过计算得到该判断矩阵的特征向量W=（0.65，0.23，0.12）即为各目标函数权重。

（2） 对目标函数进行规范化处理

通过LINGO 软件求得单个目标函数在约束条件下的极大值和极小值为

maxf1(x) = 5 918.75， minf1(x) = 4 696.2，maxf2(x) = 667.5， minf2(x) = 499.25，maxf3(x) = 3 100， minf3(x) = 2 010.

处理后的函数为

（3） 将多目标函数转化为单目标函数进行求解

通过LINGO 软件求出其最优解：x11=0，x12=250，x13=0，x14=0，x21=0，x22=0，x23=195，x24=155，x31=135，x32= 35，x33=0，x34=60。

同理，可分别建立资源2，资源3，资源4 以调度时间最小，调度路径可靠性最高，调度成本最小为目标的多目标调度模型，并通过LINGO 软件计算结果如下：

资源2：x11=0，x12=165，x13=0，x14=0，x21=0，x22=0，x23=300，x24=0，x31=185，x32= 0，x33=20，x34=175。

资源3：x11=0，x12=360，x13=0，x14=0，x21=0，x22=0，x23=290，x24=60，x31=80，x32= 0，x33=0，x34=35。

资源4：x11=0，x12=220，x13=0，x14=55，x21=0，x22=0，x23=245，x24=5，x31=100，x32= 0，x33=0，x34=150。

综上，以调度时间最小、调度路径可靠性最高、调度成本最小为目标的维修保障资源调度方案如下：

维修保障点1 的调度任务：

向作战单元2 提供250 个单位的资源1，165 个单位的资源2，360 个单位的资源3，220 个单位的资源4；向作战单元4 提供55 个单位的资源4。

维修保障点2 的调度任务：

向作战单元3 提供195 个单位的资源1，300 个单位的资源2，290 个单位的资源3，245 个单位的资源4；向作战单元4 提供155 个单位的资源1，60 个单位的资源3，5 个单位的资源4。

维修保障点3 的调度任务：

向作战单元1 提供135 个单位的资源1，185 个单位的资源2，80 个单位的资源3，100 个单位的资源4；向作战单元2 提供35 个单位的资源1；向作战单元3 提供20 个单位的资源2；向作战单元4 提供60 个 单位的资源1，175 个单位的资源2，35 个单位的资源3，150 个单位的资源4。

按以上方法得到的调度方案所对应的3 个目标函数值分别为f1(x)=18 286.25，f2(x)=2 518.75，f3(x)=10 140。若只以调度时间最小为目标得到的调度方案对应的3 个目标函数值分别为f1(x)=17 281.25，f2(x)=2 393，f3(x)=11 625。若只以调度路径可靠性最高为目标得到的调度方案对应的3 个目标函数值分别为f1(x)=18 292.5，f2(x)=2 654.5，f3(x)=10 580。若只以调度成本最小为目标得到的调度方案对应的3 个目标函数值分别为f1(x)=20 552.5，f2(x)=2 361.05，f2(x)=7 980。由以上结果比较可以发现，本文采用的方法所得到的调度方案兼顾了时间、路径可靠性、成本3 个因素对维修保障资源调度的综合影响，相比只以某一个因素为目标得到的调度方案在总体上有更好的优越性。

5 结束语

装备维修保障资源调度方案的合理与否直接影响战时装备维修保障能力。本文在分析战时装备维修保障资源调度问题的基础上，通过引入三角模糊函数，将战时维修保障资源需求量、调度时间、调度路径可靠性这些不确定信息量化，构建了多目标装备维修资源调度模型，并给出了模型求解算法。最后算例表明，本文所给出的不确定条件下装备维修保障资源调度方法，模型符合实际情况，算法具有一定合理性，为决策者开展战时装备维修资源调度提供了一定的分析角度和依据。