循环码的像构造2类新量子码

郭宏哲, 朱士信

(合肥工业大学 数学学院,安徽 合肥 230601)

0 引 言

量子纠错码理论的研究始于20世纪90年代末,文献[1-3]证明了量子纠错码的存在。随着第1个量子纠错码实例的出现,研究人员陆续提出了许多构造量子纠错码的方法,如厄米特构造、(CSS)Calderbank-Shor-Steane构造法和辛自正交构造。近年来,许多研究人员致力于利用厄米特自正交码构造良好的量子纠错码,并取得了一系列成果。文献[4]给出了常循环码是厄米特自正交码的充要条件,并利用厄米特构造得到了新的量子最大距离可分(maximum distance separable,MDS)纠错码。研究人员试图使用不同种类的纠错码来构造量子纠错码。文献[4-6]分别从常循环码、RS(Reed-Solomon)码、BCH(Bose-Chaudhuri-Hocquenghem)码中获得一些好的量子纠错码。循环码易于编码,经常被用于构造其他码,如Kerdock码、Preparata码和Justesen码。随着研究的深入,研究人员发现循环码可以构造良好的量子纠错码[7-8]。文献[9]得出qm-元循环码的q-元像也是循环码的条件。此后,循环码的像开始被用来构造量子纠错码,许多成果表明,这种构造方法有其自身的优点。文献[8]利用4m-元循环码的厄米特自正交像得到了良好的量子纠错码;文献[10]研究了qm-元码的q-元像在广义上自正交的条件,并利用4m-元循环码的自正交像构造新的量子纠错码。

本文对循环码的厄米特自正交像构造量子纠错码作了进一步研究。定义了一类映射,并给出关于循环码的像的几个性质;给出了q2m-元长度分别为n=(q2m-1)/(q-1)、n=(q2m-1)/(q2+1)(m>2偶数)的循环码的q2-元像是厄米特自正交的充分条件;对有q2m-元循环码的q2-元厄米特自正交像,使用厄米特构造得到2类新的量子循环码;与已知的量子纠错码相比,2类新的量子纠错码具有更高的码率或更大的最小距离。本文约定q是素数p的次幂。

1 基本概念

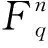
定义1 设C为长度为n的q-元线性码,则码C是循环码当且仅当对任意(a0,a1,…,an-1)∈C都有(an-1,a0,a1,…,an-2)∈C。

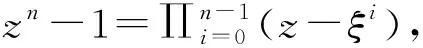
集合Cq[k,n]={k,qk,q2k,…,qlk-1k}称为包含k的q-模n分圆陪集,lk满足qlkk≡k(modn)。 若k是集合中的最小值,则称k为陪集首。集合I={0,1,2,…,n-1}可以被划分为分圆陪集I=∪k∈KCq[k,n],K是模n陪集首的集合。因此g(z)=∏k∏i∈Cq[k,n](z-ξi),其中,k遍历集合K的某子集K0。称g(z)的根ξi为码的零点。设g(z)的根的集合为T0={j|j∈∪k∈K0Cq[k,n]},并称T0为码C的零点集,即定义集。设h(z)=(zn-1)/g(z),h(z)称为C的奇偶校验多项式,h(z)的根的集合称为C的非零点集,设为T1,则T1={j|0≤j≤n-1}T0。

定义2 若g(z)是Fq上以ξb,ξb+1,…,ξb+δ-2为根的最低次首一多项式,则C=〈g(z)〉是Fq上设计距离为δ的BCH码,其中b≥0。

定理1(BCH界)[11]若C是Fq上长度为n、设计距离为δ的BCH码,则C的最小距离d≥δ。

2 循环码及其像的自正交

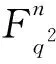
称C为厄米特自正交码当且仅当C⊆C⊥H。

容易推出C⊥H=(Cq)⊥E=(C⊥H)q。令C的非零点集为H⊆{j|0≤j≤n-1},则C⊥H仍然是循环码且有定义集-qH={-qh(modn)|h∈H}。可以推出C为厄米特自正交码的充要条件是(-qH)∩H=∅。

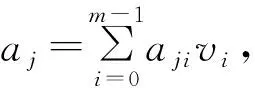
a=(a0,a1,…,an-1)=

LV(a)=(a00,…,an-1,0,a01,a11,…,an-1,m-1)。

定义参数为[n,k,d]q2m的循环码C的像LV(C)={LV(a)|a∈C}。容易推出LV(C)是参数为[mn,mk,≥d]q2的线性码。

设U={u0,u1,…,um-1}是Fq2m的1组厄米特正交基,当m为奇数时,LV(C)⊥H=LU(C⊥H);当m为偶数时,LV(C)⊥H=LU(C⊥H)q[4]。假设码C的非零点集为T2m,T2m是某些q2m-模n分圆陪集的集合。设D=〈∏t∈T2(x-ξt)〉是长度为n的q2-元循环码,其中T2=∪Cq2[k,n]⊆T2mCq2[k,n]。若D⊆D⊥H,则LV(C)⊆LV(C)⊥H。因此,-qT2∩T2=∅当且仅当对任意j、i∈T2m,t∈N,都有jq2t+1+i≡/0(modn)。

3 量子纠错码的构造

3.1 构造1

定理2(Hermitian构造)[12-13]设C是长度为n的q2-元线性码,

d=min{wt(c)|c∈C⊥HC},

若C⊆C⊥H,则存在参数为[[n,n-2k,d]]q2的量子纠错码。

设n=(q2m-1)/(q+1),m≥2,则q2m-模n分圆陪集可以表示为Cq2m[i,n]={i},其中0≤i≤n-1。考虑C是长度为n的q2m-元循环MDS码。

设

证明仅需证明对任意j、i∈T2m,t∈N,都有jq2t+1+i≡/0(modn)。

假设存在j、i∈T2m, 0≤t≤2m-1,使得jq2t+1+i≡0(modn)。注意到q4m≡1(modq2m-1),则j+iq2(2m-t-1)+1≡0(modn)。因此只需假设0≤t≤m-1。下面分2种情况讨论。

(1)m=2k≥2的情况。

当0≤t≤(m-2)/2时,

q+1≤jq2t+1+i≤

矛盾!

矛盾!

(2)m=2k+1≥3的情况。

当0≤t≤(m-1)/2时,

矛盾!

当0≤t≤(m-1)/2时,

与假设矛盾!

定理3 当n=(q2m-1)/(q-1),m≥2且m是正整数时,存在q-元[[mn,mn-2mu,≥u+1]]量子纠错码,其中1≤u≤δ1。

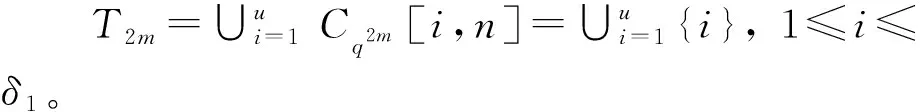
显然零点集有n-u-1个连续根ξu+1,…,ξn-1,ξn,因此C是Fq2m上一个参数为[n,u,n-u+1]的MDS循环码。C⊥H也是一个q2m-元MDS循环码,且参数为[n,n-u,u+1]。容易看出,LV(C)⊥H的距离d1≥u+1。因为LV(C)⊆LV(C)⊥H,所以可以推出LV(C)的参数为[mn,mu,≥u+1]q2。由厄米特构造知,存在参数为[[mn,mn-2mu,≥u+1]]的量子纠错码。

例1 令q=4,m=2,n=85,根据定理3,存在长度为170的四元量子纠错码。通过使用文献[14]中的加长规则,得到长度为171的四元量子纠错码。得到的量子纠错码与文献[15]中已知量子码比较,有更高的码率或更大的最小距离。结果见表1所列。

表1 四元量子码的比较

3.2 构造2

考虑C是长度为n=(q2m-1)/(q2+1)的q2m-元循环MDS码,m∈N且m>2为偶数。显然q2m-模n分圆陪集可以写为:

Cq2m[i,n]={i}, 0≤i≤n-1。

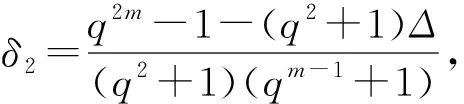
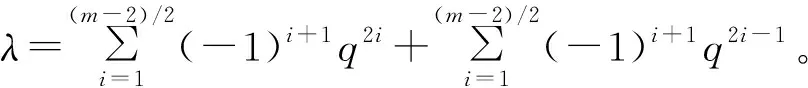
证明假设存在j、i∈T2m, 0≤t≤2m-1,使得jq2t+1+i≡0(modn)。两边同乘以q4m-2t-1,可得:

j+iq2(2m-t-1)+1≡0(modn)。

因此可以假设0≤t≤m-1。下面分2种情况讨论。

(1)m=4k≥4的情况。

当0≤t≤(m-2)/2时,

q+1≤jq2t+1+i≤

矛盾!

q+1≤j+iq2(m-t)-1≤

矛盾!

(2)m=4k+2≥6的情况。

当0≤t≤(m-2)/2时,

q+1≤jq2t+1+i≤

矛盾!

q+1≤j+iq2(m-t)-1≤

与假设矛盾!

定理4 当n=(q2m-1)/(q2+1)时,m∈N且m>2为偶数,1≤u≤δ2时,存在q-元[[mn,mn-2mu,≥u+1]]量子纠错码。

例2令q=2,m=4,n=51。根据定理4,存在长度为204的二元量子纠错码。通过使用文献[14]中的加长规则,得到长度为205的二元量子纠错码。得到的量子纠错码与文献[15]中已知量子码比较,结果见表2所列。由表2可知,得到的量子纠错码有更高的码率。

表2 二元量子码的比较

4 结 论

本文用MDS循环码的厄米特自正交像构造新的量子码。这些新的量子码具有良好的纠错性能,与文献[15]中已知的量子码相比,这些新的量子码在长度相同时具有更大的最小距离或更高的码率。因此本文具有一定的理论与应用价值。