基于时间协同的异型反舰导弹集群作战目标分配策略研究
邹智伟 邹强 尹肖云 马平原

引用格式:邹智伟,邹强,尹肖云,等.基于时间协同的异型反舰导弹集群作战目标分配策略研究[J].航空兵器,2023,30(1):19-24.
ZouZhiwei,ZouQiang,YinXiaoyun,etal.ResearchonAllocationStrategyofSpecial-ShapedAnti-ShipMissileClusterCombatTargetBasedonTimeCoordination[J].AeroWeaponry,2023,30(1):19-24.(inChinese)
摘要:针对异型反舰导弹集群作战的目标分配问题,建立了一种基于时间协同的目标分配模型。首先根据反舰作战信息,分析了导弹飞行时间差、弹-目距离和飞行速度对集群协同作战目标分配的影响,建立了一种基于导弹飞行时间标准差的时间协同优势函数,并结合距离优势与速度优势建立了综合优势函数。最后通过遗传算法求解模型最优解,仿真得到分配结果。对比分析结果表明,有时间协同优势的作战方案平均时间标准差小于无时间协同的作战方案平均时间标准差,两个算例的平均时间标准差分别下降了49.18%和63.49%,验证了模型的有效性。
关键词:反舰导弹;集群作战;目标分配;时间协同;飞行时间;优势函数;协同控制
中图分类号:TJ761;E927
文献标识码:A
文章编号:1673-5048(2023)01-0019-06
DOI:10.12132/ISSN.1673-5048.2022.0108
0引言
异型导弹集群区别于其他导弹集群,其能够充分发挥不同型号导弹的优点,适应更加复杂的作战对抗环境,能够有效提升集群作战火力打击与抗干扰能力。
同时临空是提高反舰导弹对抗作战能力的重要措施之一,保证导弹同时临空能有效提高集群的协同打击突防能力[1]。实现同时临空效果,需要对导弹集群飞行时间进行协同控制,而对集群的目标分配研究是实现集群时间协同控制方式之一。异型导弹集群通过目标分配实现导弹的时间协同,不仅需要考虑导弹的作战态势信息,还需要考虑导弹作战功能、性能的差异性,其模型更加复杂。
现有目标分配研究中,文献[2]研究了同型导弹集群的目标分配,通过蒙特卡洛方法计算导弹毁伤概率,以导弹与目标之间的距离差定义导弹之间的协同性,并以此协同性优化目标制定目标分配方案。文献[3]根据导弹集群和目标初始位置、速度、运动方向,建立带有轨迹约束的导弹命中概率模型,并在此基础上以最大毁伤效果为优化目标进行目标分配研究。文献[4-7]以集群个体的飞行路径总和最小为优化目标制定作战分配方案。文献[8-9]以无人集群作战的最短飞行时间作为优化目标,并结合距离以及任务优先等级作为约束条件,求解任务分配最优方案,同时添加限制条件避免资源倾斜。文献[10]利用层次分析法进行目标优选,再通过分配模型求解最大毁伤概率与最小耗弹量的分配方案。文献[11]以异型导弹集群的最大毁伤、最小耗弹量等多个优化指标为依据制定集群导弹的目标分配方案。
上述研究中,大多以集群中导弹最短路径之和或最小作战时间等为优化目标,而对异型导弹集群之间的时间协同问题研究较少。对异型导弹集群目标分配问题进行时间协同研究,能有效提升集群的同时临空效果,提高导弹集群的协同突防能力。因此,本文针对异型反舰导弹集群,提出了一种基于时间协同的目标分配策略,并通过遗传算法求解模型最优解,仿真得到分配结果。
1目标分配问题描述与影响因素分析
1.1问题描述
设我方有n枚反舰导弹打击敌方m艘舰艇。导弹与目标作战示意图如图1所示。
图1中,M1~Mn表示第1~n枚导弹,V1~Vn表示第1~n枚导弹的飞行速度,T1~Tm表示敌方第1~m个目标,Dij表示第i枚导弹与第j个目标之间的距离。每枚导弹以一定速度直线飞向目标。
导弹-目标分配方案可表示为分配矩阵X,即
X=x11x12…x1m
x21x22…x2m
xn1xn2…xnm(1)
式中:xij取值范围为{0,1},xij=1表示将第i枚导弹分配给j目标,xij=0表示该导弹没有分配给j目标。
1.2目标分配影響因素分析
在异型导弹集群反舰作战过程中,主要考虑的反舰导弹目标分配影响因素包括:导弹飞行时间差、弹-目距离、导弹飞行速度[11]。
(1)多枚导弹攻击同一目标时,导弹之间越接近同时临空效果,其协同攻击饱和度越高,多弹协同攻击的作战效果越好[1]。因此,分配方案中,若能使导弹同时临空,集群的协同优势就越大。
(2)反舰导弹攻击远距离目标时,导弹飞行距离越远,飞行时间越长,越容易被敌方目标拦截,造成集群整体毁伤效能下降。因此,导弹飞行距离越小,其优势越大。
(3)对反舰导弹而言,导弹飞行速度越慢,被敌方舰艇拦截的概率越高,其优势越小;导弹飞行速度越快,拦截概率越低,其优势越大。
(4)当时间协同优势较小,而导弹的距离优势、速度优势较大时,即导弹集群难以实现同时临空,而导弹个体作战优势较大,可视为该枚导弹远离导弹集群,易被目标防御系统拦截,此时无法体现导弹集群的协同作战效果,集群的综合优势较小。
2目标分配建模
2.1优势函数建立
为保证导弹集群能以最优方案打击目标,需进行合理的目标分配,同时为量化目标分配影响因素,建立优势函数。
2.1.1距离优势函数的建立
根据异型导弹集群的作战态势信息可知,导弹与目标之间的距离矩阵D为
D=d11d12…d1m
d21d22…d2m
dn1dn2…dnm(2)
式中:dij为第i枚导弹与第j个目标之间的相对距离。
根据目标分配影响因素分析可知,弹-目之间距离越小,相对作战优势越大。根据这一基本认识,可定义第i枚导弹相对第j个目标的距离优势函数为[12]
sDij=e-dijdmax(3)
式中:dmax=maxidij。
2.1.2速度优势函数的建立
由目标分配影响因素分析可知,导弹飞行速度越快,目标越难以拦截,其相对作战优势越大,因此定义速度优势函数为
sVt=e-1vi(4)
式中:Vi为第i枚导弹的飞行速度。
2.1.3时间协同优势函数的建立
为提高导弹集群作战的协同性,使得导弹打击目标更能接近同时临空效果,需建立时间协同优势函数来量化导弹集群的时间协同优势。
由导弹集群的弹-目距离与速度信息可计算出第i枚导弹相对第j个目标的剩余飞行时间:Tij=dijVi,构成剩余飞行时间矩阵T:
T=T11T12…T1m
T21T22…T2m
Tn1Tn2…Tnm(5)
异型导弹集群中,各个导弹针对目标j的时间标准差表示导弹飞行时间的离散程度,在一定程度上反映了导弹之间的进袭时间差异程度,则针对目标j的分配中,其时间标准差为
σj=1∑ni=1xij∑ni=1(Tijxij-T-J)2(6)
式中:j=1,2,…,m;TJ=1∑ni=1xij∑ni=1(Tijxij)为针对目标j分配的导弹平均飞行时间。
其时间标准差越小,导弹飞行时间的离散程度越小,导弹集群越接近同时临空目标,时间协同性越高。其变化规律与距离优势函数类似,则借鉴距离优势函数结构,为量化时间标准差与时间协同优势之间关系,定义时间协同优势函数为
STj=e-σj/A(7)
式中:σj为分配给目标j中导弹集群剩余飞行时间标准差;A为常系数,可根据专家经验给出。
当针对目标j的时间标准差σj=0时,则表示我方导弹集群能同时临空,其时间协同优势达到最大;当针对目标j的时间标准差σj越大,优势函数越小,导弹集群越难以实现同时临空,导弹集群的协同程度越低。该时间协同优势函数满足导弹飞行时间标准差对导弹集群协同作战的影响关系。
2.1.4综合优势函数的建立
首先,根据距离优势与速度优势定义可知,距离优势与速度优势相互独立,将距离优势与速度优势函数关系构建为两者之和的形式[12],且距离优势与速度优势对综合优势影响程度不同,因此需要将距离与速度优势进行权重分配。
结合上述距离优势与速度优势关系,同时依据时间协同优势函数定义,针对以下情形进行分析:
(1)当导弹集群时间协同优势函数最大,即可实现导弹集群的同时临空,根据导弹距离与速度优势函数定义,此时距离与速度优势函数不会为0,导弹通过与其他导弹实现协同保证作战效能,综合优势不会很小。
(2)当导弹集群时间协同优势较小时,即导弹之间难以实现同时临空,此时导弹之间无协同作战优势,综合优势相对较小。
考虑上述特性以及时间协同优势函数、距离优势函数、速度优势函数模型,结合无时间协同的综合优势函数模型[13],建立综合优势函数:
sij=KsTj(c1sD+c2sV)xij(8)
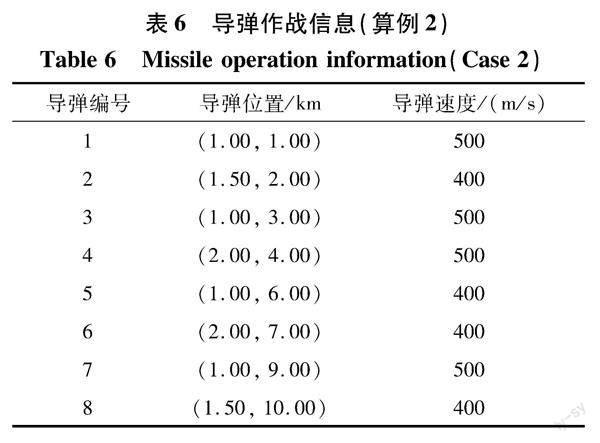
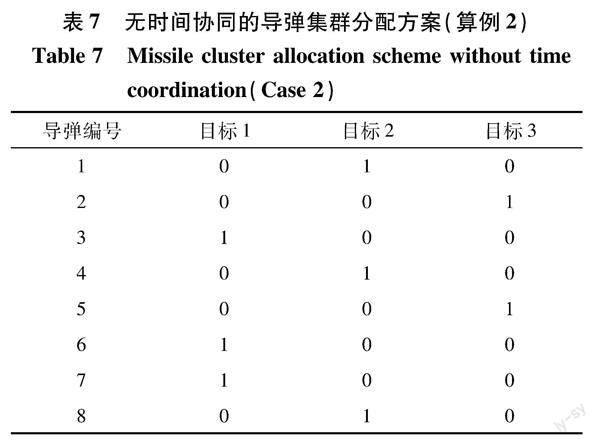
综合优势由距离优势与速度优势的和与时间协同优势的乘积组成。其中,K>0为常系数,具体数值可根据专家经验给出;c1,c2分别为权系数,其值由距离优势与速度优势函数对综合优势函数的影响程度决定,0 2.2目标分配模型的建立 针对异型反舰导弹集群,本文提出一种基于时间协同的目标分配模型。由建立的综合优势函数模型可知,目标分配的优化目标为 minF=-max∑ni=1∑mj=1sij(9) 即保證目标分配的综合优势最大。 根据反舰导弹作战性质,有以下约束条件: (1)每一枚导弹只能分配给一个目标,即 ∑mj=1xij=1(i=1,2,3,…,n)(10) (2)确保每个目标都能被打击,即 ∑ni=1xij≥1(j=1,2,3,…,m)(11) (3)为避免导弹资源的倾斜,造成分配不均的现象,加入限制条件: ∑ni=1xij≤G(j=1,2,3,…,m)(12) (4)避免资源浪费,保证我方所有导弹全部分配完毕: ∑ni=1∑mj=1xij=n(13) 3仿真设计与分析 3.1仿真算例1 针对海上反舰作战背景,现假设有3个敌方目标,我方有反舰导弹8枚。导弹集群中有4种类型导弹。 目标编号及位置分布见表1,导弹分布位置与飞行速度大小如表2所示。 在实验仿真过程中,按照上述表格数据进行仿真实验,并利用遗传算法求解相关模型的最优解。目标分配模型相关参数设定:优势函数参数设定K=100,c1=0.5,c2=0.5,A=200。约束条件参数设定:导弹数量约束G=5。 3.1.1无时间协同的目标分配模型优化仿真(算例1) 在仿真算例1中,利用遗传算法求解无时间协同目标分配模型[13]的最优解,得到综合优势函数最大值为263.53,此时对应的目标分配方案如表3所示。 在该分配方案下,针对目标1,分配了导弹2,6;针对目标2,分配了导弹4,7,8;针对目标3,分配了导弹1,3,5,针对每个目标分配的导弹数量小于5枚。在该方案下,针对目标1的导弹飞行时间标准差为56.20s;针对目标2的导弹飞行时间标准差为72.27s;针对目标3的导弹飞行时间标准差为68.08s,3个目标的导弹飞行时间标准差之和为196.55s,平均标准差为65.52s。其作战分配示意如图2所示。 3.1.2有时间协同的目标分配模型优化仿真(算例1) 利用遗传算法求解带时间协同优势模型的最优解,得到综合优势函数最大值为240.58,此时对应的目标分配方案如表4所示。 在该分配方案下,针对目标1的打击任务分配给导弹3,6;针对目标2的打击任务分配给导弹1,2,4;针对目标3的打击任务分配给导弹5,7,8,针对每个目标分配的导弹数量小于5枚。在该方案下,针对目标1的导弹飞行时间标准差为0.97s;针对目标2的导弹飞行时间标准差为23.41s;针对目标3的导弹飞行时间标准差为47.37s,3个目标的导弹飞行时间标准差之和为71.75s,平均标准差为23.92s。其作战分配示意图如图3所示。 对比两种模型仿真结果中导弹飞行时间标准差,在导弹集群中有4种类型导弹时,有时间协同优势的作战方案时间标准差小于无时间协同的作战方案优化结果,其平均时间标准差下降了63.49%。 3.2仿真算例2 针对海上反舰作战背景,现假设有3个敌方目标,我方有反舰导弹8枚。导弹集群中有2种类型导弹。 目标位置分布见表5,导弹位置分布与飞行速度如表6所示。目标分配模型相关参数设定与算例1相同。 3.2.1无时间协同的目标分配模型优化仿真(算例2) 利用遗传算法求解无时间协同优势模型的最优解,得到综合优势函数最大值为289.17,此时对应的目标分配方案如表7所示。 在该分配方案下,针对目标1的打击任务分配给导弹3,6,7;针对目标2的打击任务分配给导弹1,4,8;针对目标3的打击任务分配给导弹2,5,针对每个目标分配的导弹数量小于5枚。在该方案下,针对目标1的导弹飞行时间标准差为43.37s;针对目标2的导弹飞行时间标准差为42.10s;针对目标3的导弹飞行时间标准差为0.42s,3个目标的导弹飞行时间标准差之和为85.89s,平均标准差为28.63s。其作战分配示意图如图4所示。 3.2.2有时间协同的目标分配模型优化仿真(算例2) 利用遗传算法求解含时间协同优势模型的最优解,得到综合优势函数最大值为185.37,此时对应的目标分配方案如表8所示。 在该分配方案下,针对目标1的打击任务分配给导弹2,5,6;针对目标2的打击任务分配给导弹1,7,8;针对目标3的打击任务分配给导弹3,4,针对每个目标分配的导弹数量小于5枚。在该方案下,针对目标1的导弹飞行时间标准差为1.00s;针对目标2的导弹飞行时间标准差为41.62s;针对目标3的导弹飞行时间标准差为1.03s,3个目标的导弹飞行时间标准差之和为43.65s,平均标准差为14.55s。其作战分配示意图如图5所示。 對比两种模型优化结果可知,有时间协同优势模型得到的作战方案平均时间标准差小于无时间协同的作战方案优化结果,其平均时间标准差下降了49.18%。 3.3仿真分析 根据上述两个算例分析可知,通过与无时间协同优势的目标分配算例相比,有时间协同优势的目标分配算例表明:在保证满足作战约束条件的基础上,缩短了导弹集群的进袭时间差、提高了导弹集群同时临空效果、提升了导弹集群协同突防打击优势,符合战场实际需求,证明了有时间协同优势目标分配模型的有效性。 4结论 本文针对海上反舰作战的异型导弹集群时间协同目标分配问题进行了一定的探索性研究。首先在目标分配模型的建立上,分析了导弹飞行时间差、导弹-目标距离、导弹飞行速度对导弹集群作战影响,提出了一种基于反舰导弹飞行时间标准差的时间协同优势函数,以此反映导弹集群的时间协同优势,再结合距离优势函数与速度优势函数,构成综合优势函数作为目标分配模型的优化目标,并依据导弹集群作战理论,建立模型约束条件,最后通过遗传算法求解模型的优化结果,并对比无时间协同优化模型与有时间协同优化模型结果,验证了含有时间协同的目标分配模型的有效性。 参考文献: [1]卢发兴,焦安龙,贾正荣.反舰导弹饱和攻击时差规律研究[J].电光与控制,2015,22(5):46-48. LuFaxing,JiaoAnlong,JiaZhengrong.LawofTimeDifferenceinAnti-ShipMissileSaturationAttack[J].ElectronicsOptics&Control,2015,22(5):46-48.(inChinese) [2]钟建林,宁德旭,邹强.反舰导弹协同突防近防炮在线目标分配算法[J].兵器装备工程学报,2019,40(9):12-16. ZhongJianlin,NingDexu,ZouQiang.AlgorithmofOnlineTargetAssignmentforAnti-ShipMissilesCooperativelyPenetratingClose-QuartersCannons[J].JournalofOrdnanceEquipmentEngineering,2019,40(9):12-16.(inChinese) [3]白建保,尹栋,谢海斌,等.基于命中概率模型的反舰导弹:目标分配方法研究[J].舰船电子工程,2021,41(7):34-39. BaiJianbao,YinDong,XieHaibin,etal.ResearchonAnti-ShipMissile-TargetAssignmentMethodBasedonHitProbabilityModel[J].ShipElectronicEngineering,2021,41(7):34-39.(inChinese) [4]邓道靖,马云红,龚洁,等.基于并行GAPSO算法的多无人机协同任务规划[J].电光与控制,2016,23(11):18-22. DengDaojing,MaYunhong,GongJie,etal.CooperativeMissionPlanningofMultipleUAVsBasedonParallelGAPSOAlgorithm[J].ElectronicsOptics&Control,2016,23(11):18-22.(inChinese) [5]张梦颖,王蒙一,王晓东,等.基于改进合同网的无人机群协同实时任务分配问题研究[J].航空兵器,2019,26(4):38-46. ZhangMengying,WangMengyi,WangXiaodong,etal.CooperativeReal-TimeTaskAssignmentofUAVGroupBasedonImprovedContractNet[J].AeroWeaponry,2019,26(4):38-46.(inChinese) [6]张富震,朱耀琴.复杂环境中多无人机协同侦察的任务分配方法[J/OL].系统仿真学报,2021.https://doi.org/10.16182/j.issn1004731x.joss.21-0552. ZhangFuzhen,ZhuYaoqin.TaskAllocationMethodforMulti-UAVCooperativeReconnaissanceinComplexEnvironment[J/OL].JournalofSystemSimulation,2021.https://doi.org/10.16182/j.issn1004731x.joss.21-0552.(inChinese) [7]JiaTao,XuHaihang,YanHongtao,etal.DecentralizedMulti-AgentTaskPlanningforHeterogeneousUAVSwarm[J].TransactionsofNanjingUniversityofAeronauticsandAstronautics,2020,37(4):528-538. [8]SteczW,GromadaK.UAVMissionPlanningwithSARApplication[J].Sensors,2020,20(4):E1080. [9]苏梅梅,程咏梅,胡劲文,等.基于改进蚁群算法的无人机集群任务分配和路径规划联合优化[J].无人系统技术,2021,4(4):40-50. SuMeimei,ChengYongmei,HuJinwen,etal.CombinedOptimizationofSwarmTaskAllocationandPathPlanningBasedonImprovedAntColonyAlgorithm[J].UnmannedSystemsTechnology,2021,4(4):40-50.(inChinese) [10]楊晓,王玉玫.基于AHP和遗传算法的导弹作战任务分配问题研究[J].计算机与数字工程,2018,46(3):459-464. YangXiao,WangYumei.ResearchontheAllocationofMissileCombatMissionsBasedonAHPandGeneticAlgorithm[J].Computer&DigitalEngineering,2018,46(3):459-464.(inChinese) [11]陈思,胡涛.基于多目标优化遗传算法的武器-目标分配[J].舰船电子工程,2015,35(7):54-57. ChenSi,HuTao.Weapon-TargetAssignmentwithMulti-ObjectiveNon-DominatedSetRankingGeneticAlgorithm[J].ShipElectronicEngineering,2015,35(7):54-57.(inChinese) [12]吴森堂.导弹自主编队协同制导控制技术[M].北京:国防工业出版社,2015:89-99. WuSentang.CooperativeGuidance&ControlofMissilesAutonomousFormation[M].Beijing:NationalDefenseIndustryPress,2015:89-99.(inChinese) [13]安炳合,寇佳禹,王永骥,等.基于改进烟花算法的多导弹目标分配方法[J].弹箭与制导学报,2020,40(3):113-118. AnBinghe,KouJiayu,WangYongji,etal.AMulti-TargrtsAllocationMethodBasedonImprovedFireworksAlgorithm[J].JournalofProjectiles,Rockets,MissilesandGuidance,2020,40(3):113-118.(inChinese) ResearchonAllocationStrategyofSpecial-ShapedAnti-ShipMissile ClusterCombatTargetBasedonTimeCoordination ZouZhiwei1,ZouQiang1*,YinXiaoyun1,MaPingyuan2 (1.NavalUniversityofEngineering,Wuhan430033,China;2.Unit92840ofPLA,Qingdao266000,China) Abstract:Aimingattheproblemoftargetallocationinoperationsofspecial-shapedanti-shipmissileswarms,atargetallocationmodelbasedontimecoordinationisestablished.Firstly,accordingtotheanti-shipcombatsituationinformation,theinfluenceofmissileflighttime,missile-to-targetdistanceandflightvelocityonthetargetallocationofclustercoordinationoperationsisanalyzed,andatimecoordinationadvantagefunctionbasedonthestandarddeviationofmissileflighttimeisestablished,andthecomprehensiveadvantagefunctionisformedintegratedthedistanceadvantagefunctionwithvelocityadvantagefunction.Finally,theoptimalsolutionofmodelisdeducedbygeneticalgorithm,andtheallocationresultsaregottenbysimulation.Theresultsofcomparativeanalysisshowthatthestandarddeviationofaveragetimeofoperationschemewithtimecoordinationislowerthanthatwithouttimecoordination.Thestandarddeviationofaveragetimefortwocasesdescendsabout49.18%and63.49%.Thesimulationresultsverifythevalidityofthemodel. Keywords:anti-shipmissile;clustercombat;targetallocation;timecoordination;flighttime;advantagefunction;collaborativecontrol 收稿日期:2022-05-24 基金项目:国防科技创新特区项目(19-H863-05-ZD-013-001-02) 作者简介:邹智伟(1998-),男,湖北孝感人,碩士研究生。 *通信作者:邹强(1977-),男,江西宜丰人,博士,副教授,硕士生导师。

