有控弹箭稳定性边界的解析预测模型
常思江 李东阳


引用格式:常思江,李东阳.有控弹箭稳定性边界的解析预测模型[J].航空兵器,2023,30(1):11-18.
ChangSijiang,LiDongyang.AnalyticalPredictionModelofStabilityBoundaryforGuidedProjectiles[J].AeroWeaponry,2023,30(1):11-18.(inChinese)
摘要:针对弹箭在控制力作用下的稳定性问题,对有控弹箭稳定性边界的解析预测模型进行研究。通过对弹轴系纵轴向角速度的线性化,在弹轴系下建立了有控弹箭角运动方程;通过对弹轴系与非滚系之间滚转角的线性化,在非滚系下建立了五阶角运动方程。根据线性系统稳定性理论,分别推导出弹轴系和非滚系下的稳定性边界解析预测模型。对两种模型在多种工况下开展了仿真分析,结果表明,所提出的弹轴系模型可用于升弧段和降弧段,但控制方位角的应用范围受限;而非滚系模型不受控制方位角范围限制,预测精度较好,但只能用于降弧段,且控制力过大对模型精度产生不利影响;实际工程中建议对两种模型进行综合应用。
关键词:有控弹箭;控制力;角运动;稳定性;弹轴坐标系;非滚转坐标系
中图分类号:TJ760
文献标识码:A
文章编号:1673-5048(2023)01-0011-08
DOI:10.12132/ISSN.1673-5048.2022.0219
0引言
随着精确打击和低间接伤害概率逐渐成为现代战争对弹药武器的基本要求,各类低成本弹道修正弹、制导炮弹、制导航弹等有别于一般导弹的有控弹箭应运而生,目前已广泛用于航炮、舰炮、地炮等武器系统,具有较高的效费比[1]。
由于这类有控弹箭主要是在相应的无控弹箭平台基础上通过制导化改造而成,故自20世纪70年代末以来,研究人员就十分关注弹箭在控制力作用下的稳定性和动力学响应等问题[2-4],针对各种有控弹箭开展了相关研究。Wernert等[5]对鸭式布局双旋稳定弹的稳定性判据进行了研究;Corriveau等[6]针对脉冲发动机控制弹箭,研究了双脉冲策略下的弹体响应特性;Cooper等[7]研究了鸭式布局非对称尾翼弹的稳定性问题。国内外学者近年来针对鸭式布局(含固定舵和可偏转舵)双旋弹这类有控弹箭,对自由运动[5]、强迫运动[8]、弹体对控制力和重力的动态响应[9]、法向力计算模型[10]、质心偏移运动特性[11]、全弹道动态稳定性[12]、控制稳定性[13]等方面开展了深入研究。此外,Hu等[14]利用傳递函数研究了捷联导引头延时所引起的弹箭锥形运动不稳定;Li等[15]研究了弹道修正弹的稳定控制力边界问题。
从研究方法角度,上述研究主要是基于攻角方程,通过各种简化对攻角方程实施近似解析求解,从而得到相关的稳定性判据等。为了验证相关解析解的有效性,往往还需对刚体弹道模型进行数值计算,由此也引出一重要的学术问题。
Lloyd等[2]通过数值计算发现,对具有头部控制力的有控弹箭(如鸭式布局双旋弹,其头部与后体通过滚动轴承连接,可实现差动滚转),控制力的作用会引起弹体章动和进动不稳定,而传统的外弹道线化理论却无法解释数值计算中出现的这种现象。研究表明[2-3],这其实与角运动建模的坐标系选取有关。弹箭角运动建模,可选择弹轴坐标系(以下简称弹轴系)或非滚转坐标系(以下简称非滚系)。若采用反旋电机等部件,可近似实现头部控制力相对于惯性系(如地面坐标系)保持方向不变[2,11-13],则在非滚系内建模,必然引入新的变量(滚转角度N),如忽略该变量,将无法预测上述不稳定现象;在弹轴系内建模,存在纵轴向角速度的问题(表现为弹体俯仰角和摆动角速度的耦合),若忽略该纵轴向角速度,则等效于在非滚系内建模。以往研究常假设俯仰角为零(即水平射击),这与实际中“控制力往往在弹道降弧段作用”的工况具有较大差异。
对此,Lloyd等[2]首先在非滚系下建模,对弹轴系与非滚系之间的滚转角进行简化,并利用线性化理论研究了角运动方程的特征根,进而给出控制力在水平和铅直方向的稳定范围。针对同一问题,Murphy[3]认为,不必从弹轴系转换到非滚系也能得到相应结果,他通过引入共轭变量,采用拟线性法求出复攻角方程的特征根,据此给出控制力诱导出的最大平衡攻角之稳定边界。Li等[15]针对弹道修正弹的控制力稳定边界问题,通过补偿矩阵对控制力和重力的影响在弹轴系内进行了补偿,但并未深究不同坐标系下建模的本质差异。
文献[2-3,15]所研究的问题本质上可概括为“有控弹箭稳定性边界的解析预测”。“稳定性边界”是指只要控制力大小在边界范围内,则可保证受控弹箭的稳定飞行;而“解析预测”是指利用角运动方程,通过解析方式找到相应的边界值。该研究可为有控弹箭总体方案的初步设计提供理论依据。根据上述分析,该问题的关键在于坐标系。简言之,Lloyd等[2]认为不能在弹轴系内建模而只能在非滚系中建模;Murphy[3]和Li等[15]则都认为可在弹轴系内建模,只不过需针对具体方程做一些修正。此外,上述文献仅针对弹道降弧段工况进行了研究,而实际上在弹道升弧段进行控制也是需要的(如对于防空类弹药)。
为从弹道学机理角度厘清上述问题,本文以一类具有前(头部)、后(弹身)两体双旋结构的旋转稳定弹道修正弹为研究对象(其头部可提供弹道控制所需的法向力),将在弹轴系和非滚系下分别建立计及控制作用的弹箭角运动模型,根据线性系统稳定性理论,推导稳定性边界的解析预测模型,考察升弧段和降弧段两类工况,据此分析不同坐标系下所得结果的优势和局限性,以期为该问题的机理研究及有控弹箭总体方案设计等提供参考。
1不同坐标下的弹箭角运动方程
1.1坐标系简介
弹箭攻角运动方程的建模可在弹轴系或非滚系下进行。由于弹轴系和非滚系是从地面坐标系(简称地面系)和弹体坐标系(简称弹体系)得到,故本节先介绍地面系和弹体系。
地面系原点A取为炮口中心;ZE轴沿重力方向,向下为正;XE轴与重力方向垂直,指向弹体的速度方向为正;YE轴由右手法则确定。通常将地面系(AXEYEZE)平移至弹体质心,得平动坐标系(OXEYEZE)。
弹体系与弹体固联,原点位于弹箭质心O;X轴与弹体纵轴重合,指向头部为正;Y轴在弹翼对称平面内与X轴垂直,从弹尾向前看去,向右为正;Z轴方向按右手法则确定。弹体系(OXYZ)可由平动坐标系经欧拉转换,依次绕Z轴、Y轴和X轴旋转弹体偏角ψ、俯仰角θ和滚转角得到。
弹轴系的Y轴始终在水平面内,为此,将弹体系绕X轴转过滚转角-即得弹轴系(OXYAZA);非滚系X轴的角速度始终为零,故将弹轴系绕X轴转过滚转角N,使X轴的角速度为零,即得到非滚系(OXYNZN)。需要说明的是,滚转角N是一個人为定义的角度,与飞行器俯仰角、偏航角、滚转角等姿态角相比,并非一可视化的姿态角,其物理意义在于:角速度N恰与弹轴系X轴的自转角速度抵消,从而保证非滚系X轴的自转角速度为零,使得角运动建模过程得以简化。
值得说明的是,对于双旋稳定弹的控制力,在弹轴系内建模,模型相对准确但计算不便;在非滚系内建模,模型误差稍大但计算方便。因此,本文在两种坐标系下开展研究,以便为不同应用场合提供适用的模型和算法。
1.2弹轴坐标系下的角运动方程
设弹箭在弹轴系下的角速度三分量分别为p,q,r,则弹轴系纵轴向(X轴)的角速度可表示为
Ωx(s)=-rdVtanθ(1)
式中:d为弹径;V为来流速度;s为无量纲弹道弧长,s=∫Vdt/d,t为弹箭飞行时间;θ为弹体俯仰角。
对于本文研究的有控弹箭,作用在弹体上的控制力和力矩如图1所示。
如图1所示,NC和MC分别为控制力和控制力矩;控制力作用点至弹体质心的距离为XC(定义控制力作用点位于质心之前为正,XC>0);φP为控制力NC相对于地面系铅直轴(重力方向)的方位角。
控制力在弹轴系中的表达式为
FCxFCyAFCzA=NC0sinφP-cosφP(2)
控制力矩在弹轴系中的表达式为
MCxMCyAMCzA=XCNC0cosφPsinφP(3)
当控制力很小或为零时,角速度Ωx(s)≈0;但对于控制力较大的情形,Ωx(s)值不可忽略,否则会引起文献[2]所示的误差。
设攻角在弹轴系下的分量为高低攻角α和方向攻角β,则θ=θV+α,其中θV为弹道倾角;同时,将攻角角速度近似等于弹体横向角速度,即r≈-β·,q≈α·。因此,为方便后续求平衡点,对式(1)做如下近似:
Ωx(s)=β′tan(θV+α)≈β′[tanθV+(1+tan2θV)α](4)
取状态变量
x=[αα′ββ′]T(5)
式中:“′”表示对无量纲弧长s的一阶导数。
根据外弹道理论[16],在弹轴系下建立以时间t为自变量的横向运动方程,为
v·=Fay+Fnaym-(uΩz-Ωxw)
w·=Faz+Fnazm-(vΩx-Ωyu)
q·=May+MnayIy-(σpΩz-Ωxr)
r·=Maz+MnazIy-(Ωxq-σpΩy)(6)
式中:Ωx,Ωy,Ωz为弹轴系相对于地面系的角速度分量;其余符号同前。
定义复攻角ξ=(v+iw)/V和复弹体摆动角速度μ=(q+ir)(d/V),取无量纲弹道弧长s=∫Vdt/d为自变量,则可将式(6)写成复数形式,即
ξ′+V′V+iΩxdVξ-iuVμΩ=(Fy+iFz)dmV2μ′+V′V+iΩxdVμ-iσpdVμΩ=(My+iMz)d2ItV2(7)
式中:
μΩ=(Ωy+iΩz)(d/V),可认为μΩ≈μ;
Fy+iFz=mAV2(Cy+iCz)/d+(Fnay+iFnaz);
My+iMz=Ak-2t·(Cm+iCn)ItV2/d2+(Mnay+iMnaz);(Cy+iCz)为侧向气动力系数,(Cm+iCn)为侧向气动力矩系数,限于篇幅,两者的具体表达式从略。
从式(7)中第1式解出μ,将其关于s求一阶导数可得μ′,将μ和μ′代入式(7)中第2式,经推导得到只含有复攻角ξ的角运动方程,为
ξ″+[H-i(P1-P2)]ξ′-[M-P1P2+i(PT-P′2+S1)]ξ=(Ry+iRz)(8)
式中:P1=P-Ωx(s);P2=Ωx(s)+P20;P=σpd/V;P20=PACNpα/σ+ACSN;等号右端的Ry和Rz是与控制力和重力有关的项,其具体表达式较冗长,这里从略;其余符号同前。
由于攻角α≈v/V和β≈w/V,式(8)可化为以α,α′,β,β′为状态变量的状态空间形式的角运动方程(一阶微分方程组),将式(4)与Ry,Rz的具体表达式代入其中,忽略影响较小的重力项,并记x1=α,x2=α′x3=β,x4=β′,可得
x′=[x2x′2x4x′4]T(9)
式中:
x′2=(M-[-Ω2x+(P-P20)Ωx+PP20])x1-(PT-Ω′x+S1)x3-(P-P20-2Ωx)x4-Hx2+Rz0+RzΩΩx;
x′4=(M-[-Ω2x+(P-P20)Ωx+PP20])x3+(PT-Ω′x+S1)x1+(P-P20-2Ωx)x2-Hx4+Ry0+RyΩΩx;
Ry0=(-FCyAkC+FCzAP+F′CyA)B;
Rz0=(-FCzAkC-FCyAP+F′CzA)B;
RyΩ=-FCzAB;RzΩ=FCyAB;
kC=xCk-2t+Ak-2tCMq;xC=XC/d;
H=-Ak-2t(CMq+CMα·)+ACNα;
M=Ak-2tCMα+A2CNαk-2tCMq;
S1=Ak-2tCSM+A2CSNk-2tCMq;
T=T0-ΩxPH1;T0=1σAk-2tCMpα+ACNα;
H1=H+Ak-2tCMα·;
P=σpdV;P20=PACNpασ+ACSN;
A=ρSd2m;B=dmV2;k-2t=md2It。
其中:m為弹箭质量;S为弹体横截面积;ρ为弹箭所处位置的大气密度;σ=Ix/It,Ix和It分别为弹体的轴向和横向转动惯量;CMq为赤道阻尼力矩系数;CMα·为下洗延迟力矩系数;CNα为法向力系数;CMα为俯仰力矩系数;CSN为诱导侧向力系数;CSM为诱导侧向力矩系数;CNpα为马格努斯力系数;CMpα为马格努斯力矩系数。
1.3非滚转坐标系下的角运动方程
在非滚系下建立角运动模型时,为了准确地计及控制力的影响,相对于地面系方向固定的控制力在向非滚系的三个轴进行投影时,必须考虑滚转角度N的影响,此时会出现N的三角函数,使得角运动方程在非滚系内出现几何非线性。对此,考虑到一般情况下N不断变化且量值较小,可对N进行小角度假设,即sinN≈N,cosN≈1,以消除几何非线性。
因此,控制力在非滚系中的三分量为
FCxFCyNFCzN≈0FCyA+FCzAN-FCyAN+FCzA(10)
控制力矩在非滚系内的三分量为
MCxMCyNMCzN≈0(-FCzA+FCyAN)XC(FCzAN+FCyA)XC(11)
设非滚系下的速度分量为(u,v,w),令α=v/V表示非滚系内攻角的高低分量,β=w/V表示非滚系内攻角的侧向分量,且由于θ=θV+α,故可近似取θ′≈α′。
采用文献[16]中角运动建模的一般思路,经繁杂的推导,可得到非滚系下的弹箭横向运动方程组为
β′=Fay+FnaymdV2-uVr^-βV′V
α′=Faz+FnazmdV2+uVq^-αV′V
q^′=May+MnayItd2V2-σp^r^-q^V′V
r^′=Maz+MnazItd2V2+σp^q^-r^V′V
′N=(q^sinN+r^cosN)tanθ(12)
式中:p^=pd/V;q^=qd/V;r^=rd/V;Fay,Faz,May,Maz为作用在弹箭上的空气动力和力矩;Fnay,Fnaz,Mnay,Mnaz为重力和控制力,即
Fay=dmV2[-ACNαβ+(p^ACNpα+ACSN)α+
A(CNq+CNα·)r^];
Faz=dmV2[-ACNαα-(p^ACNpα+ACSN)β-
A(CNq+CNα·)q^;
May=d2ItV2[Ak-2tCMαα+Ak-2t(p^CMpα+CSM)β+
Ak-2t(CMq+CMα·)q^];
Maz=d2ItV2[-Ak-2tCMαβ+Ak-2t(p^CMpα+CSM)α+
Ak-2t(CMq+CMa·)r^];
Fnay=FCyN+mgcosθ·N;
Fnaz=FCzN+mgcosθ;
Mnay=MCyN;Mnaz=MCzN。
式中:CNq为弹轴摆动引起的俯仰阻尼力系数;CNα·为下洗延迟俯仰阻尼力系数。关于CNq和CNα·的具体描述可参见文献[17]。
根据小角度假设,对式(12)的最后一式做如下近似:
′N≈r^tanθ(13)
为便于建模,这里取状态变量为
x=βαq^r^NT(14)
将控制力和力矩表达式(10)~(11)、气动力和力矩的具体表达式代入式(12),并结合式(13),经推导、整理,可得非滚系下的五階角运动方程为
x′=Kx+Q(15)
式中:
K=LNp0NqF3NpL-Nq0-F2MpMMq-PM3-MMpPMq-M2000tanθ0;
Q=[F2,F3,M2,M3,0]T;
矩阵K和矩阵Q中元素的具体表达式为
L=-ACNα
M=Ak-2tCMα
Mp=Ak-2t(p^CMpα+CSM)
Np=p^ACNpα+ACSN
Mq=Ak-2t(CMq+CMα·)
Nq=A(CNq+CNα·)-1
F2=FCyAB
F3=FCzAB
M2=-xCk-2tFCzAB
M3=xCk-2tFCyAB。
值得说明的是,本文通过对滚转角N进行线性化得到的上述五阶角运动方程,相较于文献[15]中的六阶角运动方程,降低了计算复杂度。
2稳定性边界的解析预测模型
根据上述不同坐标下的弹箭角运动方程,利用线性系统的稳定性理论,推导相应的稳定性边界预测模型。
2.1弹轴坐标系下的解析预测模型
对弹轴系下的弹箭角运动方程式(9),求其平衡点为
xe=δMRz0-δTRy00δMRy0+δTRz00(16)
式中:δM=-M~M~2+(PT0+S1)2;δT=(PT0+S1)M~2+(PT0+S1)2;M~=M-P·P20;下标“e”表示“平衡点”。
在平衡点附近进行局部线性化,可得平衡点的Jacobian矩阵为
Je=0100M~-H-(PT0+S1)RC20001PT0+S1P~M~RC4(17)
式中:
P~=P-P20;RC2=(-P~·x1e+H1·x3e+RzΩ)Ωx1-P~;RC4=(-P~·x3e-H1·x1e+RyΩ)Ωx1-H;Ωx1(x1e)=tanθV+(1+tan2θV)x1e;
x1e和x3e分别表示状态变量x1和x3对应的平衡点。
由上式可见,控制力出现在RC2和RC4中,从而影响平衡点的特征根。因此,可通过特征根来分析控制力对弹箭角运动稳定性的影响。
系统的特征多项式可表达为
d4λ4+d3λ3+d2λ2+d1λ+d0=0(18)
式中:
d4=1;d3=H-RC4;d2=-2M~-P~RC2-HRC4;d1=-M~(H-RC4)+(PT0+S1)(P~-RC2);d0=M~2+(PT0+S1)2。
根据线性系统稳定性理论中的Routh判据,在控制力作用下,若弹箭角运动在平衡点附近是稳定的,则弹箭的结构参数、气动参数以及控制参数等,需满足以下条件:
di>0,i=0,1,2,3d2d3-d1>0d1d2d3-d23d0-d21>0(19)
由于控制力和控制力矩参数出现在系数d1,d2及d3中,则利用不等式组式(19),可确定弹箭在某一飞行条件下允许的控制参数范围。这里,控制参数组合为(FyC,FzC,xC),也可采用(NC,φP,xC)的组合形式,两者通过式(2)~(3)进行换算。
2.2非滚转坐标系下的解析预测模型
由非滚系下的弹箭角运动方程式(15)可知,与控制力(矩)有关的项(即F2,F3,M2,M3)包含在系数矩阵K中。根据线性系统稳定性理论,通过求解K的特征根可判断系统的稳定性,进而确定控制力的稳定范围。
弹箭角运动系统的平衡点为
xe=-K-1Q(20)
系统的特征多项式为
d5λ5+d4λ4+d3λ3+d2λ2+d1λ+d0=0(21)
式中:
d0=tanθ{
[-(LM-MpNp)P+(LMp+MNp)Mq]F2+[(LM+MpNp)Mq+(LMp-MNp)P+(M2+M2p)Nq]F3+
[-Mq(L2-N2p)-(LM-MpNp)Nq]M2+[-P(L2-N2p)-(LMp+MNp)Mq]M3};
d1=(P2+M2q)(L2-N2p)+(M2+M2p)N2q+2LNq(MMq+PMp)+
tanθ{(2LP+MpNq)M3+(L2-N2p+2LMq+MNq)M2+(-LM-MpNp-MMq-PMp)F3+[-(LMp+MNp)+MP-MpMq]F2};
d2=-2[(L2-N2p)Mq+L(P2+M2q)+(LM+MMq+PMp)Nq]+tanθ·[MF3+F2Mp-PM3-(2L+Mq)M2];
d3=L2-N2p+P2+M2q+4LMq+2MNq+M2tanθ;d4=-2Mq-2L;d5=1。
仍采用Routh判据,可得非滚系内弹箭角运动稳定所必须满足的条件为
di>0,i=0,1,2,3,4d4d3-d2>0d2(d4d3-d2)-d4(d4d1-d0)>0d4d1-d0>0(22)
當仅考虑水平方向的控制力FCyA时,即FCzA=0,则F3=0且M2=0,从上述di的表达式可知,只有di(i=0,1,2)中含有控制力F2和力臂系数xc(定义xc=xC·k-2t),故可将F2和xc分离出来,即等价表达为如下形式:
di=di0+dic·F2(23)
式中:dic=dic0+dicc·xc。限于篇幅,di0,dic0,dicc的具体表达式从略。
于是,不等式组式(22)可改写为
di>0,i=3,4di0+dicF2>0,i=0,1,2-d2cF2+d3d4-d20>0a2F22+a1F2+a0>0(d4d1c-d0c)F2+d4d10-d01>0(24)
式中:
a2=-d22c;
a1=d3d4d2c-d24d1c+d4d0c-2d20d2c;
a0=d3d4d20-d24d10+d01d4-2d220。
只要给出控制力的作用位置XC,控制力F2的稳定范围就可通过求解不等式组式(22)或式(24)得到。
3仿真与分析
至此,推导出了弹轴系下的稳定性边界解析预测模型式(19)和非滚系下的稳定性边界预测模型式(22)或式(24)。为验证模型的有效性,开展仿真分析。
3.1仿真条件
以某105mm旋转弹[15]为例,假设在弹道降弧段进行控制,对应的弹道参数和气动力系数如表1所示。其中,LCG为弹体重心至弹顶的距离,以弹径的倍数计。据此计算出角运动方程的系数,如表2所示。
除上述外,本节仿真中还考虑控制力作用位置在θV=±43°处(弹道升弧段和降弧段)、弹体左旋(取p=-1050rad/s)的工况,并给出相应的仿真结果。
3.2结果与分析
(1)弹轴系解析模型的仿真结果与分析
将表1~2中的系数代入不等式组式(19),可得控制力参数组(NC,φP,xC)的可行范围,如图2所示。
图2中,蓝色对应不等式d1>0,青色对应不等式d2>0,绿色对应不等式d3>0,红色对应不等式d2d3-d1>0,黄色对应不等式d1d2d3-d23d0-d21>0;竖轴的数值为不等式符号左端的取值。不难看出,后两个不等式(红色和黄色)起主要作用。
图3~4分别给出了弹道升弧段(θV=43°)和降弧段(θV=-43°)工况下,不同控制方位角φP对应的稳定控制力NC的范围。同时,转速取p=±1050rad/s。
图3(a)和图4(a)均为控制方位角φP的极坐标表示,p=1050rad/s对应弹体右旋,p=-1050rad/s对应弹体左旋。
由图可知,对于升弧段,所推导模型只能预测右旋弹在φP∈(0°,180°)时的NC稳定边界,而无法预测φP∈(180°,360°)时的NC稳定边界,对于左旋弹却正好相反;对于降弧段,模型只能预测右旋弹在φP∈(180°,360°)时的NC稳定边界,而无法预测φP∈(0°,180°)时的NC稳定边界,左旋弹也正好相反。
根据第1.2节关于控制力的描述,NC可表示控制力的幅值(值域为[0,+∞]),控制力方向由φP表征。若控制力作用位置为弹顶(xC=2.96),考察p=1050rad/s时的降弧段工况,利用解析模型可计算得到:当φP=90°时,控制力的稳定边界为4.9N;当φP=270°时,控制力的稳定边界为37.27N。只有当控制力小于对应边界值时,才可实现稳定的角运动。同时,对未采取任何近似的方程组式(12)(可认为是精确模型)进行数值积分,所得结果为:当φP=90°时,控制力的稳定边界为55N;当φP=270°时,控制力的稳定边界为37N。显然,解析模型与精确模型对稳定控制力一侧边界(φP=270°)的预测结果十分吻合,但对另一侧(φP=90°)则差异较大。这也是该解析模型的主要缺点。但相比于现有文献中的模型,该模型既可求解降弧段(θV<0)工况,又可求解升弧段(θV>0)工况。
值得说明的是,方程组式(12)来自于6自由度刚体弹道方程组,未作任何简化,只是对应于某一特征点(速度V为常数)。对方程组式(12)进行数值积分,本质上等同于对6自由度刚体弹道方程组在相应特征点上进行数值求解。因此,通过数值积分方程组式(12)来验证解析计算模型是合理、可行的。
根据第2节的理论分析,稳定控制力只能在平衡点附近的一定邻域内满足稳定性,无法保证在任何条件下均实现稳定运动。
(2)非滚系解析模型的仿真结果
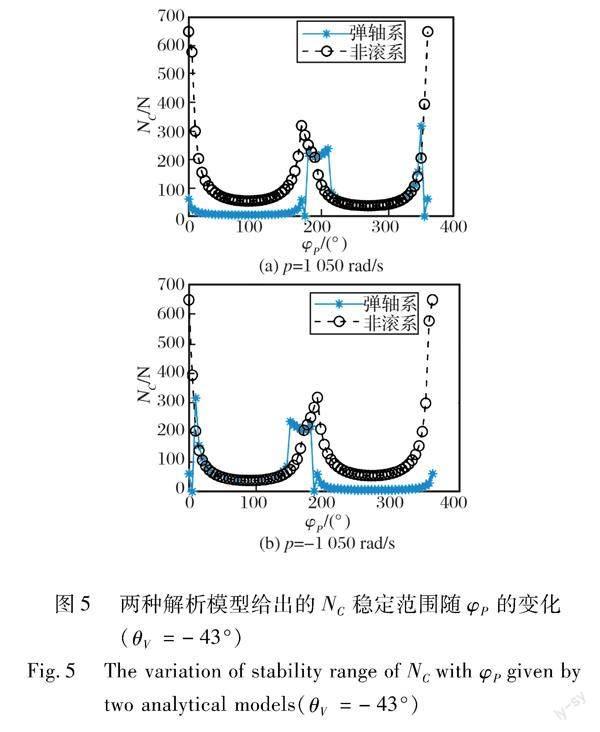
这里仍以上述105mm旋转弹为例。由于非滚系解析模型无法计算弹道升弧段工况,故仅给出降弧段(θV=-43°)工况下不同控制方位角φP对应的稳定控制力NC的范围,仍取p=±1050rad/s。将上述结果与弹轴系解析模型在相同条件下的计算结果进行对比,如图5所示。
由图5可知,对于降弧段工况,两种坐标系下的模型对于右旋时相对于铅垂平面向左的控制力稳定范围、左旋时相对于铅垂平面向右的控制力稳定范围,给出了相同的估计结果(可称为有效估计结果)。
取p=1050rad/s,θV=-43°,xC=2.96为条件,由解析模型计算可得:对于水平控制力NC·sinφP,当φP=90°时,控制力的稳定边界为53.65N;当φP=270°时,控制力的稳定边界为36.87N。由此可知,图5所示两种模型的有效估计结果与前述方程组式(12)的数值积分结果较为吻合。可见,本文利用小角度假设对滚转角N进行线性化是合理、可行的。与弹轴系模型相比,非滚系模型消除了对控制方位角φP应用范围的限制,这是该模型的优势,但其缺点在于无法应用于θV>0的升弧段。当θV>0时,判别式(24)的解为空集,但对方程组式(12)进行数值积分,仍可得到稳定控制力的边界。
值得注意的是,由于非滚系模型在推导过程中,对滚转角N进行了小攻角假设,因而上述结论只在N不太大时成立(如N<60°)。从五阶角运动方程式(15)及其平衡点表达式(20)可知,N的稳态值只涉及α,β的方程,故N的稳态值大小与控制力的大小有关。当控制力的模值越大,N也越大,并且攻角α,β也越大,此时线性化系统式(15)就和原系统相差较大,不能很好地预测角运动方程的稳态值,很可能会出现过估计的现象,这就限制了稳定性判据不等式(22)的应用范围。
4结论
本文针对作用在有控弹箭上的相对于惯性系方向固定的控制力,提出了弹轴系和非滚系下的两个稳定性边界解析预测模型,用于估计控制力对弹箭角运动稳定性的影响,可量化给出稳定控制力的边界范围。
通过对比、分析两个坐标系下的模型,总结出两者各自的优势和不足:
(1)与现有文献模型相比,本文所建立的弹轴系模型可应用于升弧段和降弧段两种工况;不足之处在于其给出的稳定控制力上、下界,只有其中一个足够准确,而另一个却由于近似处理的原因而退化为无效。
(2)由于本文所提出的非滚系模型是一个五阶方程,相较于文献中的六阶方程,降低了计算复杂度。在降弧段,该模型对稳定控制力的预测结果与数值积分结果吻合较好;不足之处在于其不能用于升弧段。此外,滚转角N的大小和控制力大小密切相關,过大的控制力会产生较大的N,导致小角度假设失效,影响分析结果的准确性。
在实际应用中,建议根据所研究有控弹箭的弹道特点、战术技术要求等,同步利用上述弹轴系模型和非滚系模型开展稳定性边界预测,在对两个模型的计算与分析结果进行综合考量后,作为理论设计的依据。
参考文献:
[1]王中原,史金光,常思江,等.弹道修正弹技术发展综述[J].弹道学报,2021,33(2):1-12.
WangZhongyuan,ShiJinguang,ChangSijiang,etal.ReviewonDevelopmentofTechnologyofTrajectoryCorrectionProjectile[J].JournalofBallistics,2021,33(2):1-12.(inChinese)
[2]LloydKH,BrownDP.InstabilityofSpinningProjectilesduringTerminalGuidance[J].JournalofGuidanceandControl,1979,2(1):65-70.
[3]MurphyCH.InstabilityofControlledProjectilesinAscendingorDescendingFlight[J].JournalofGuidance,Control,andDyna-mics,1981,4(1):66-69.
[4]OllerenshawD,CostelloM.SimplifiedProjectileSwerveSolutionforGeneralControlInputs[J].JournalofGuidance,Control,andDynamics,2008,31(5):1259-1265.
[5]WernertP.StabilityAnalysisforCanardGuidedDual-SpinStabilizedProjectiles[C]∥AIAAAtmosphericFlightMechanicsConference,2009:5843.
[6]CorriveauD,WeyP,BernerC.ThrustersPairingGuidelinesforTrajectoryCorrectionsofProjectiles[J].JournalofGuidance,Control,andDynamics,2011,34(4):1120-1128.
[7]CooperG,FresconiF,CostelloM.FlightStabilityofanAsymme-tricProjectilewithActivatingCanards[J].JournalofSpacecraftandRockets,2012,49(1):130-135.
[8]常思江,王中原,刘铁铮.鸭式布局双旋稳定弹强迫运动理论研究[J].兵工学报,2016,37(5):829-839.
ChangSijiang,WangZhongyuan,LiuTiezheng.ATheoreticalStudyofForcedMotionforDual-Spin-StabilizedProjectileswithCanards[J].ActaArmamentarii,2016,37(5):829-839.(inChinese)
[9]ChangSJ.DynamicResponsetoCanardControlandGravityforaDual-SpinProjectile[J].JournalofSpacecraftandRockets,2016,53(3):558-566.
[10]钟阳,王良明,李岩,等.旋转稳定二维修正弹鸭舵法向力计算模型研究[J].弹道学报,2019,31(2):48-54.
ZhongYang,WangLiangming,LiYan,etal.CalculationModelofNormalForceofCanardonSpinStabilizedTwo-DimensionalTrajectoryCorrectionProjectile[J].JournalofBallistics,2019,31(2):48-54.(inChinese)
[11]ChangSJ,LiDY,WeiW.SwerveSolutionforSpin-StabilizedProjectileswithCanards:ARevisit[J].JournalofSpacecraftandRockets,2021,58(5):1352-1360.
[12]赵新新,史金光,王中原,等.固定鸭舵双旋弹全弹道动态稳定性及其影响因素[J].力学学报,2022,54(5):1364-1374.
ZhaoXinxin,ShiJinguang,WangZhongyuan,etal.DynamicStabilityandInfluenceFactorsoftheWholeTrajectoryofFixedCanardDual-SpinProjectiles[J].ChineseJournalofTheoreticalandAppliedMechanics,2022,54(5):1364-1374.(inChinese)
[13]赵新新,史金光,王中原,等.固定鸭舵双旋弹角运动特性与控制稳定性研究[J].哈尔滨工业大学学报,2022,54(1):123-131.
ZhaoXinxin,ShiJinguang,WangZhongyuan,etal.StudyonAngularMotionCharacteristicsandControlStabilitywithFixedCanardDual-SpinProjectile[J].JournalofHarbinInstituteofTechnology,2022,54(1):123-131.(inChinese)
[14]HuX,YangSX.ConingMotionInstabilityofSpinningMissilesInducedbytheDelayofStrap-DownSeeker[J].ChineseJournalofAeronautics,2020,33(12):3360-3368.
[15]LiRP,LiDG,FanJR.ResearchonInstabilityBoundariesofControlForceforTrajectoryCorrectionProjectiles[J].MathematicalProblemsinEngineering,2019,2019:6362835.
[16]韓子鹏,常思江,史金光.弹箭非线性运动理论[M].北京:北京理工大学出版社,2016.
HanZipeng,ChangSijiang,ShiJinguang.NonlinearMotionTheo-ryofProjectileandRocket[M].Beijing:BeijingInsitituteofTechnologyPress,2016.(inChinese)
[17]McCoyRL.ModernExteriorBallistics[M].Atglen:SchifferPublishingLtd.,1999.
AnalyticalPredictionModelofStabilityBoundaryfor
GuidedProjectiles
ChangSijiang*,LiDongyang
(CollegeofEnergyandPowerEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,China)
Abstract:Aimingattheproblemofprojectilestabilityundertheactionofcontrolforce,thispaperstudiedtheanalyticalpredictionmodelofstabilityboundaryforguidedprojectiles.Bylinearizingthelongitudinalaxialangularvelocityofbodyaxiscoordinate,theangularmotionequationunderthebodyaxiscoordinateisestablished.Throughlinearizingtherollanglebetweenthebodyaxiscoordinateandnon-rollingcoordinate,afive-orderequationofangularmotionisproposedunderthenon-rollingcoordinate.Usingthestabilitytheoryoflinearsystem,theanalyticalpredictionmodelofstabilityboundaryunderthebodyaxiscoordinateandnon-rollingcoordinateareobtained.Simulationsofthetwomodelsundervariousworkingconditionsareconducted.Resultsindicatethattheproposedmodelunderthebodyaxiscoordinatecanbeappliedintherisingarcsegmentandthefallingarcsegment,whereasthecontrolforceorientationislimited.Themodelunderthenon-rollingcoordinateisnotlimitedbythecontrolforceorientation,andthepredictionaccuracyisgood.Thedrawbackofthismodelisthatitcanonlybeusedforthefallingarcsection,anditsaccuracywillbeharmfullyaffectedbyexcessivecontrolforce.Itissuggestedthatthetwomodelsshouldbeappliedcomprehensivelyinpracticalengineering.
Keywords:controllableprojectiles;controllableforce;angularmotion;stability;bodyaxiscoordinate;non-rollingcoordinate
收稿日期:2022-10-17
基金项目:瞬态冲击技术重点实验室基金项目(6142606183107)
*作者简介:常思江(1983-),男,广西恭城人,博士,副研究员。

