反舰导弹类型的Bayes-可拓识别模型

王 丰 林 瑜 农元苑

海军航空大学，山东烟台 264001

反舰导弹[1-2]可以从地面、水面舰艇和潜艇、飞行器等多种武器系统上发射，自问世以来,其在近现代的历次海战中都发挥了重要作用。使用反舰导弹对舰艇进行饱和攻击是当前对舰攻击的主要方式。在舰艇对反舰导弹的作战中，最主要的技术难点是目标反舰导弹类型的识别，如果能较早识别反舰导弹的类型，会对其飞行的精确路径跟踪、威胁度的评估及舰艇防御方案的制定与决策均有积极的意义。

文献[3-4]利用贝叶斯方法对反舰导弹的类型和身份识进行了研究。该方法是在考虑各误判损失发生的先验概率和误判损失的前提下，用探测的反舰导弹数据修正先验概率的分布函数，进而识别反舰导弹的身份或类型。Bayes-可拓方法在许多领域，取得了一些应用成果。本文将可拓学中的可拓识别方法[5]与Bayes方法[6-8]相结合，提出了一种反舰导弹类型识别方法，即考虑了Bayes方法的优点，又考虑了各识别特征指标与各反舰导弹类型总体特征指标的“关联”契合程度。使反舰导弹类型识别过程中考虑的因素更多、更全面。较其它识别方法，精确度更高，结果更符合实际情况，为反舰导弹的类型识别提供了一个新视角。

1 反舰导弹类型识别的Bayes-可拓方法

1.1 基本思路及步骤

1.1.1 流程图

通过对Bayes方法和可拓识别方法的总结、梳理，得到反舰导弹类型识别的Bayes-可拓方法流程如图1。

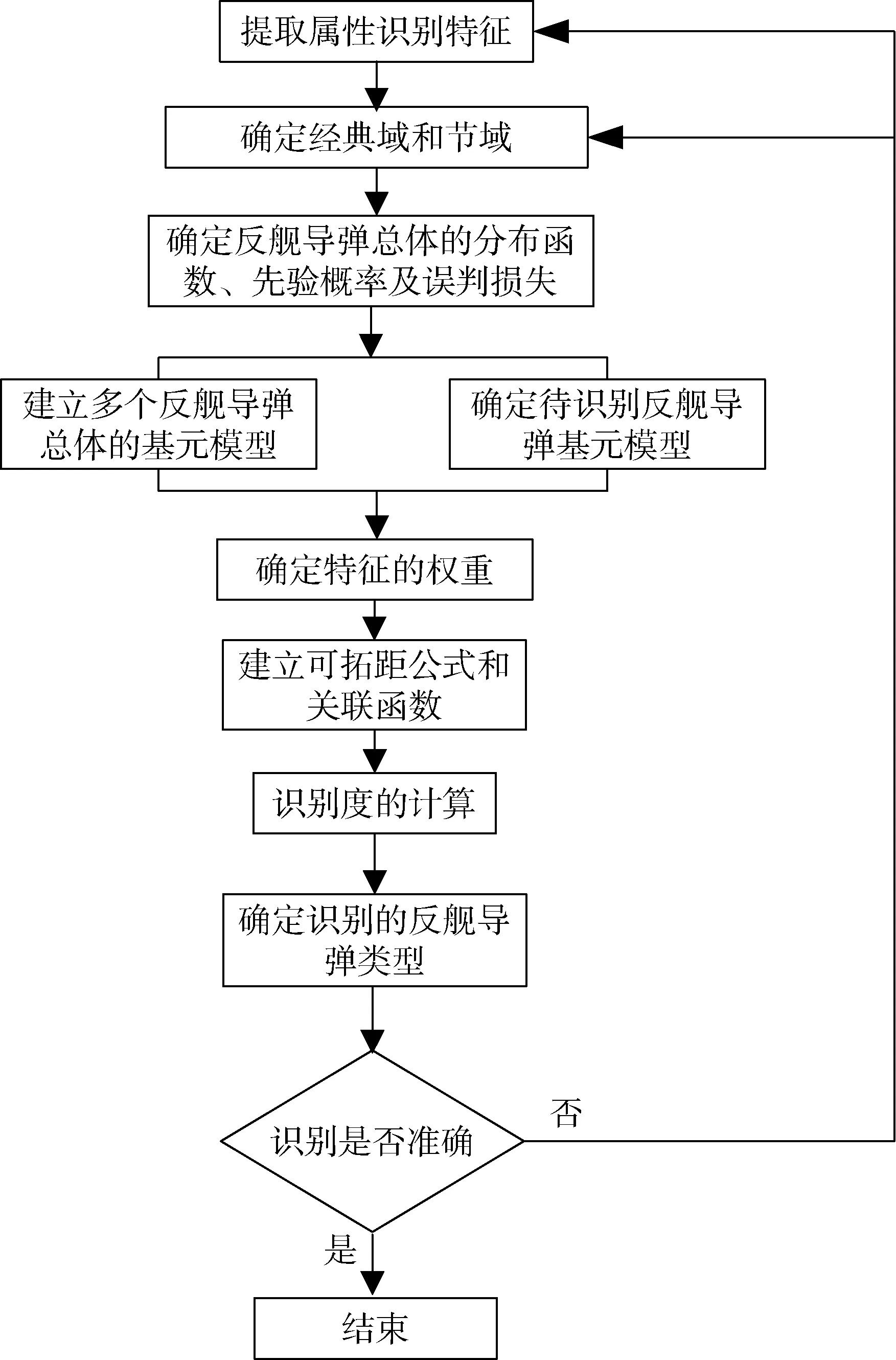
图1 敌反舰导弹类型识别的Bayes-可拓方法

1.1.2 步骤

1)构建反舰导弹总体的基元模型,确定分布函数及误判损失

反舰导弹类型识别涉及因素较多，通常，识别反舰导弹类型的属性特征有目标速度、目标机动性、目标飞行高度、导引头雷达的发散频率、脉冲宽度和脉冲重复频率等。根据情报和各种有效传感器的测量数据[3]，得到反舰导弹的先验信息及属性特征量值，建立m个反舰导弹的总体Zi(i=1,2,…,m)，并用基元模型[9]刻画为

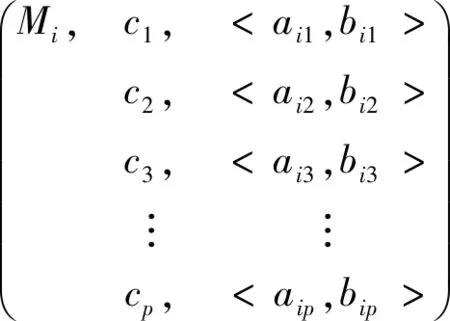
(1)

其中，Mi为待识别的第i(i=1,2,…,m)个反舰导弹；ci(i=1,2,…,p)为描述反舰导弹Zi(i=1,2,…,m)的p个识别特征指标；Vi=为待识别敌反舰导弹Mi(i=1,2,…,m)关于识别特征指标ci(i=1,2,…,p)所规定的量值域范围，即经典域[9-10]。

(2)

对敌反舰导弹的类型发生误判，必将造成反舰导弹威胁度的评估结果、我方拦截方案的制定和决策发生错误的判断。统一将将其误判损失记为C(l/j)，有

C(l/j)≥0，l,j=1,2,…,r

(3)

C(l/l)=0，l=1,2,…,r

(4)

2)建立待识别反舰导弹的基元模型

根据情报和各种传感器的测量数据，结合参考文献，得到待识别反舰导弹M特征的各项量值，从而用基元，建立其模型为

RX=(M，C，VX)=

(5)

其中，vi(i=1,2,…,p)为待识别反舰导弹M关于p个识别特征ci(i=1,2,…,p)所测量得到的具体数值。

3)构建可拓距公式和关联函数

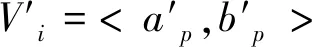
(6)

(7)

根据可拓距公式，构建待识别反舰导弹关于p个识别特征的关联函数[5,9-10,12]

(8)

4)权重的计算

权系数表示p个识别特征指标对反舰导弹类型确定的影响程度，权系数越大，表示影响程度越大。在反舰导弹[13-14]类型识别特征指标确定后，根据组合赋权法、模糊评价法等方法确定p个识别特征指标的权系数。并分别记为φr(r=1,2,…,p)，其中

(9)

5)构建识别度函数

在可拓距、关联函数和权系数的基础上，建立各反舰导弹总体Zi(i=1,2,…,m)的综合识别度函数[5]

(10)

6)确定反舰导弹的识别结果

通过将传感器及各种途径得到的各项特征数据，代入相应计算公式，得到综合识别度函数值Ki(M)。

如果考虑识别的先验概率及误判损失，则构建反舰导弹的识别度计算公式，为

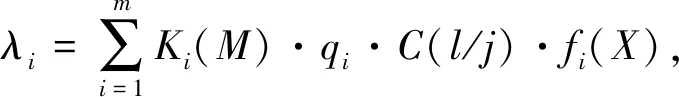
(11)

将得到的量值代入公式(11)中，得到待识别反舰导弹的识别度。

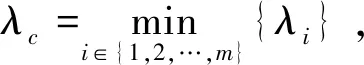
2 实例仿真研究

通过仿真实验环境，对来袭反舰导弹的实例分析，验证本文方法的有效性和全面性。

本文选取目标速度c1、目标机动性c2、目标飞行高度c3、导引头雷达的发散频率c4、脉冲宽度c5和脉冲重复频率c66个属性特征作为识别特征[4]。经过传感器数据和情报数据的汇总分析[15-16]，得到来袭反舰导弹1、2关于c1，c2，c3，c4，c5，c66个识别特征指标的量值，如表1。

表1 两枚反舰导弹关于识别特征指标的量值

假设通过训练数据的仿真路径分析[17-18]，构建反舰导弹飞行路径的分布函数[9]为

的正态分布。确定先验概率，分别记为

q1=0.12，q2=0.22，q3=0.23，q4=0.26，q5=0.17

得到反舰导弹类型识别的误判损失量值，见表2。

根据仿真训练数据集，将各特征指标数据进行数量级统一处理后，建立反舰导弹的经典域基元为Zi(i=1,2,3,4,5)，刻画为

根据5个经典域范围数据，构建反舰导弹类型的节域基元模型

计算各识别特征指标的权重，分别记为

δ1=0.19，δ2=0.225，δ3=0.147，δ4=0.18，δ5=0.123，δ6=0.135。

1)若不考虑先验概率和误判损失的情况，只运用可拓识别方法，根据所建立的经典域和节域模型，并将表1相应数据代入公式(6)～(9)，得到反舰导弹1和2的综合识别度分别为

K1(1)=0.558，K2(1)=0.68，K3(1)=0.625，K4(1)=0.492，K5(1)=0.471；K1(2)=0.612，K2(2)=0.532，K3(2)=0.497，K4(2)=0.762，K5(2)=0.548。

有

可见，反舰导弹1属于类型二，反舰导弹2属于类型四。

2)若考虑先验概率和误判损失，通过仿真，得到2枚反舰导弹类型的Bayes-可拓识别度仿真图，如图2。

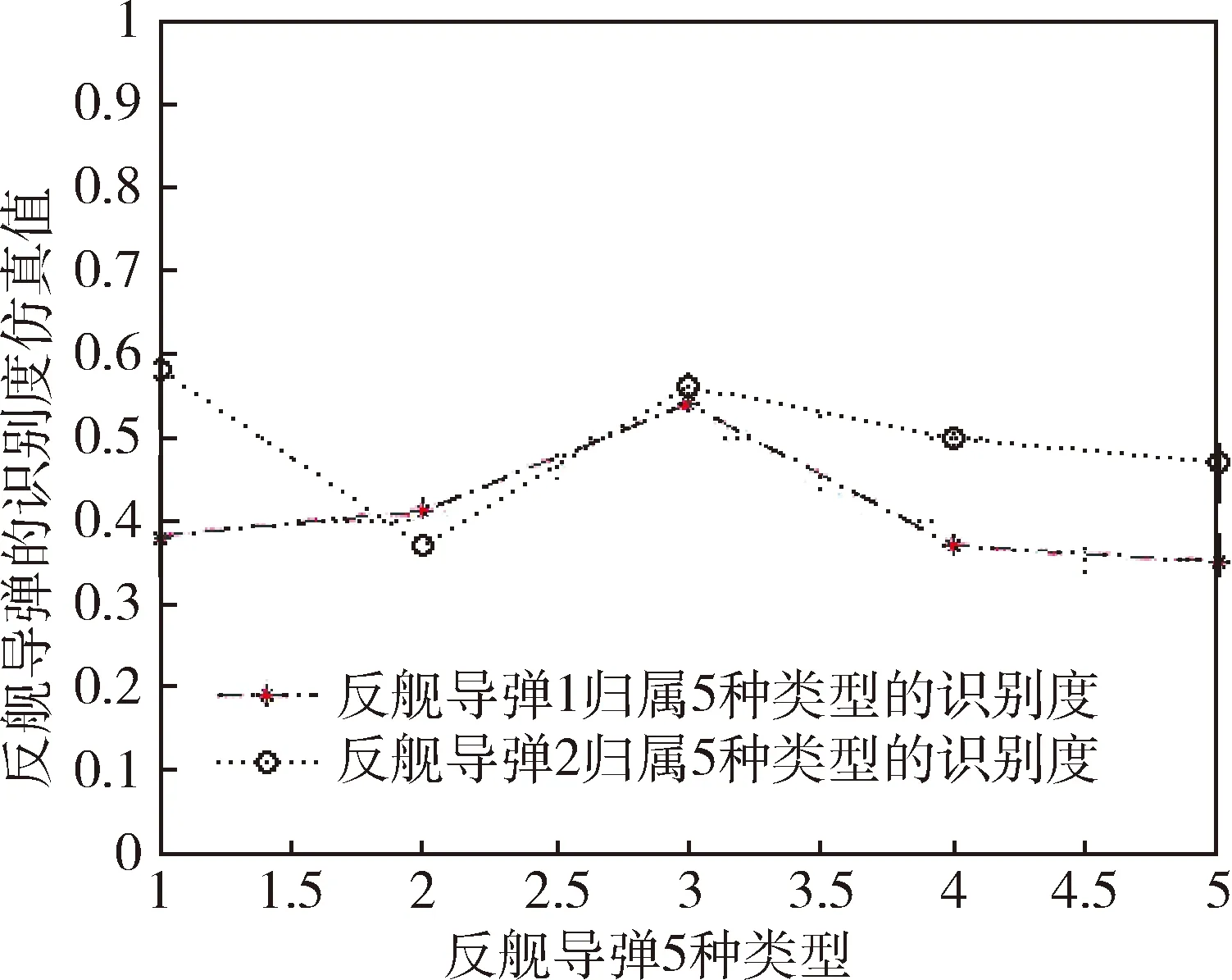
图2 两枚反舰导弹关于5种类型识别度的仿真

从仿真图中可见：

1)反舰导弹1的类型识别度仿真结果为λ5<λ4<λ1<λ2<λ3，该反舰导弹为类型五。

2)反舰导弹2的类型识别度仿真结果为λ2<λ5<λ4<λ3<λ1，该反舰导弹为类型二。

通过上述分析，在考虑先验概率和误判损失前后，2枚反舰导弹的类型归属不同。较可拓识别方法，该方法考虑问题更加全面，识别结果更令人满意。

3 结束语

在Bayes方法和可拓识别方法的基础上，提出了一种反舰导弹类型的Bayes-可拓识别方法。该方法使考虑的因素更加全面，识别结果更令人满意，为反舰导弹威胁度的评估、拦截方案决策的制定提供了参考。由于训练集样本数量不够充分，导致关联函数的构建不够准确,这都需要在后续日常演习、仿真训练过程中重点解决。