在“鸡兔同笼”教学中培养学生创新意识的探索

【摘要】本文聚焦小学数学教学中的“鸡兔同笼”问题模型，探讨培养学生创新意识的策略方法，提炼出两点实践经验：一是基于学生的基础认知，引导学生通过对常规方法的归纳、类比发现“假设思想”应用的规律，建立“鸡兔同笼”问题解决的基本模型，初步培养学生的创新意识；二是创设新的问题情境，引导学生基于问题解决基本模型，探索一些非常规的问题解决思路和方法，进一步培养和发展学生的创新意识和能力。

【关键词】小学数学 “鸡兔同笼” 模型意识

创新意识

【中图分类号】G63 【文献标识码】A

【文章编号】0450-9889（2023）04-0065-04

创新意识是《义务教育数学课程标准（2022年版）》（以下简称《2022年版数学课标》）提出的三个方面数学核心素养在小学和初中阶段的具体表现之一，主要表现为主动尝试从日常生活、自然现象或科学情境中发现和提出有意义的数学问题，包括“初步学会通过具体的实例，运用归纳和类比发现数学关系与规律”“提出數学命题与猜想，并加以验证”“勇于探索一些开放性的、非常规的实际问题与数学问题”等。培养学生的创新意识，有助于学生形成独立思考、敢于质疑的科学态度与理性精神。

“鸡兔同笼”问题是1 500年前我国古代数学名著《孙子算经》中记载的一种数学趣题，也是一种较为典型的数学问题模型，该模型不仅可用于解决“鸡兔同笼”的基础问题，而且可用于解决生活中类似的“人马问题”“租船问题”等。“鸡兔同笼”问题安排在人教版四年级下册的“数学广角”，笔者尝试在“鸡兔同笼”教学中培养学生的创新意识，进行了一些实践探索，积累了一定的教学经验。

一、基于学生的基础认知，引导学生通过对常规方法的归纳、类比发现“假设思想”应用的规律，建立“鸡兔同笼”问题解决的基本模型，初步培养学生的创新意识

四年级的学生已经积累了一定的数学活动经验，掌握了一定的数学思想方法。本课开始，笔者决定从简单的问题入手，引导学生完全凭借自己的理解和现有认知经验去寻找解决问题的路径和方法，然后同组之间进行平等交流，从中提炼出问题解决的基本模型，培养创新意识。在学生独立思考、合作学习的过程中，笔者不给出任何提示。

在课堂教学中，笔者立足教材，先给学生讲解了“鸡兔同笼”问题的来历，再从简单的问题入手引出教材中的例题1：“笼子里有若干只鸡和兔。从上面数，有8个头，从下面数，有26只脚。鸡和兔各有几只？”接下来让学生根据题目中给出的条件自行“猜测”两种动物的数量；再借助题目中给出的数量关系进行合理分析，得出问题解决的方法和结论；最后在班级中展开讨论。在学生独立思考、合作学习的过程中，教师侧重引导学生在列表填数和画图思考的过程中认清定量和变量，培养有序思考的习惯，顺势归纳“极端假设”的方法，形成解决一类问题的基本模型，发展问题解决能力。

学生在自主学习、合作探究的过程中，总共给出了三种问题解决的方法。第一种是猜测列表法，第二种是画图法，第三种是算术法。

（一）猜测列表法中的有序思维

针对猜测列表法的形成过程，笔者与相关学生展开了下面的课堂对话。

师：请问你是如何得出这个结果的？

生1：我其实是胡乱分配数量的。我想，只要它们的和满足了8只这个条件就行，于是我先猜测可能有5只鸡、3只兔。但是，在计算两种动物的脚数时我发现5只鸡、3只兔总共才有22只脚。

师：这个结果便与题目中给出的总脚数发生了冲突。接下来该怎么办呢？

生1：我发现这样算出的总脚数比实际总脚数少了，因为每只兔是4只脚，每只鸡只有2只脚，每只兔子的脚数多于每只鸡的脚数，所以，我前面的猜测，应该是兔的只数猜少了、鸡的只数猜多了。

师：条分缕析，分析得头头是道！既然知道问题出在哪里了，你接下来是怎么做的？

生1：我就增加兔的只数呗。我再猜兔6只、鸡2只。但是，结果还是对不上，总的脚数又多了。于是我只好再减掉一只兔，变成兔5只、鸡3只，这一次总算对上了。

师：千辛万苦，总算是对上了！老师为你不屈不挠的精神点赞！不过，你这种方法虽然可行，但你变换鸡和兔的只数的过程有点过于随意，缺乏章法，这样的思考通常效率低、成本高。你虽然能得出结果，但探究过程带有极强的偶然性，因为本题中鸡和兔的总只数较少。如果在第一次试取数对失败之后，我们按照一定的顺序增减调试，效果会更好，特别当我们遇到较大的数的时候，尤其需要有序地思考和调试。比如，首次猜测失败后，我们在首次猜测的基础上减去1只鸡、增加1只兔，变成4只鸡4只兔。这时的总脚数有24只了，但与总脚数相比，仍然欠缺2只，于是继续调整，再减1只鸡、追补1只兔，变成3只鸡、5只兔，这时，鸡和兔的总脚数才刚刚好是26只。虽然这个过程仍然并不简单，但它是有序地思考，不容易出现遗漏的情况。

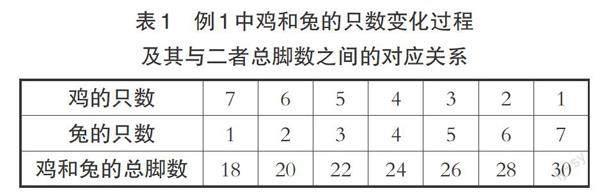
教师一边与学生进行课堂对话，一边用表格方式记录双方的问答，在明晰了“猜测—验证—反思—推理”的思维过程与方法的同时，拓展数据“鸡7兔1”“鸡1兔7”，呈现出如表1所示的整体思维框架暨鸡和兔的只数变化过程及其与二者总脚数之和的对应关系；接着引导学生围绕表格中“哪些元素发生了变化？”“哪些元素没有发生变化？”展开数据分析和讨论。学生在讨论中发现：首先，表格中变化的元素是鸡和兔各自的只数以及它们的总脚数，变化的规律是“每把1只鸡替换成1只兔，鸡的只数减少1，兔的只数便会相应增加1，而鸡和兔的总脚数就会增加2只”“每把1只兔替换成1只鸡，兔的只数减少1，鸡的只数便会相应增加1，而鸡和兔的总脚数就会减少2只”。其次，不变的元素是鸡和兔的总只数8以及鸡和兔的总脚数26，这是题目的既定条件，无法更改。

针对上述猜测法，教师进行了如下小结：大家可以先随意猜测一个数对，只要符合鸡和兔的总只数为8就行；然后一步一步增减调整，直到总脚数也符合既定的条件26即可。这种方法还真是管用，一道千年趣题居然就这么轻易地被大家破解了。那咱们以后就将这种自创的方法固定下来，作为解决“鸡兔同笼”问题的一种通用公式，如何？（生表示赞同）不过，这种不断增减数据的方法多少有点烦琐，咱们能不能找到一种更为简便的方法呢？

（二）画图法中的“极端假设”思想及其与算术法的推演关系

随着教师的引问，又一名学生出示了本组的问题解决方法——画图法，如图1所示。

生2：我先画了8只鸡，计算下来共有16只脚，和实际的总脚数相比，少了10只脚。因为1只鸡比1只兔少2只脚，于是我就在1只鸡上面添加2只脚，将它变成一只兔子，按照同样的方法变鸡为兔，结果我发现，只有将5只鸡变成兔时，才能补足缺少的10只脚。于是，我最终确定了兔的只数是5、鸡的只数是3。

生3：我和她画图的方法刚好相反。如图2所示，我先画了8只兔，算出共有32只脚，比实际脚数多了6只。这就说明，兔的只数画多了，只能通过将其中部分兔变成鸡，才能使鸡和兔的总脚数变小，又因为1只兔比1只鸡多2只脚，我给每只兔子擦去2只脚使它变成鸡，这样一共擦去了3只兔子的总共6只脚，才使结果与条件达成了一致。于是我的结论是，共有5只兔、3只鸡。

师：这样看来，画图法似乎比猜测法更为直观。那么这种办法是不是最好的方法呢？将它作为最终的解题通用公式，你们意下如何？（学生表示同意）其实，无论是上面的猜测法还是画图法，其中都隐含了一种假设的思想：先随意假设一种情况或假设一种极端情况，再对照条件对假设情况进行调整，使之最终合乎题目中隐含的数量关系，进而得出正确的结果。在画图法中，还隐含了一种“极端假设”的思想，就是把笼子里的动物全部假设为一种动物，要么全是鸡，要么全是兔。其实，“极端假设”与下面的算术法联系更为紧密。

接下来，教师板书运用算术法进行计算的过程：（1）先假设全是鸡，于是总脚数有8×2=16只，与条件中的总脚数尚有一定距离，尚缺脚数26-16=10只，这说明，笼子中不可能全是鸡，还有一部分兔子被误认成了鸡；而1只兔被误认为1只鸡便会少4-2=2只脚，尚缺的10只脚实际来自10÷2=5只兔；于是兔的只数是5，鸡的只数是8-5=3。（2）然后也可以假设全是兔……（解题过程略）

教师最后小结“极端假设”思想下例1中鸡和兔的只数变化过程及其与二者总脚数之间的對应关系，如表2所示。

数形结合的思想方法在数学教学中有广泛的应用，通常的应用情形有两种，一种是“以数解形”，一种是“以形助数”。所谓“以数解形”，指的是借助数的精确性来阐明形的某些属性；所谓“以形助数”，指的是借助形的几何直观性来阐明数之间的某种关系。基于小学生以具象思维为主的思维特点，“以形助数”在小学数学教学中有着更为广泛的应用。上面的教学过程，让学生自己思考解决问题的方法，学生除了运用“假设”的思想方法，运用画图法的学生还灵活运用了“以形助数”的数学思想方法。的确，让学生一下子想到算术法，无异于建筑“空中楼阁”，缺乏学情基础。在学生自主、合作尝试以后，教师适时引导，推出算术法便水到渠成了。在学生没有任何经验可供借鉴和没有任何现成模型支撑的前提下，运用常规的猜测法随机猜测时，教师适时引导学生学会“有序”猜测、合理猜测，在确保总只数为8、总脚数是26的前提下，学会用“渐变”的眼光看待问题，发展逻辑思维，从而为后面算术法的形成建立了思维模型；之后结合学生画图法的几何直观，通过添加鸡的脚数和削减兔的脚数来实现鸡和兔之间的“身份”转换，进一步发展学生的逻辑思维。用列表的方式呈现猜测法和画图法的有序思维过程，让学生联想到“极限法”，引出“极端假设”思想；从假设全部是兔（8只兔）这个极端情况起，通过不断增减两种事物的只数，一直推演到另一个极端（8只鸡），便为算术法的形成打下了思维发展的基础。其实，算术法的出现，就是以极端情况为基准，先计算出极端情况下的总脚数与实际脚数的差，然后基于每只鸡和兔的脚数的差，算出极端情况下的总脚数与实际脚数相差的具体量，最终确定鸡的只数和兔的只数。显然，算术法具有更强的抽象性和逻辑性，学生甚至可以根据这个公式计算出任何一道“鸡兔同笼”问题。因此，算术法才是数学学习所要追寻的问题解决的基本模型。

二、创设新的问题情境，引导学生基于问题解决基本模型，探索出一些非常规的问题解决思路和方法，进一步培养和发展学生的创新意识和能力

在得出上述问题解决基本模型之后，学生对假设思想有了更深的感悟。教师止步于此，也算初步达成了教学目标。但是，“鸡兔同笼”问题的确是一道千古趣题，让学生从解决此类题目的过程中，沿着“极端假设”的思想更进一步，找到新的解题方法，感受数学问题解决的趣味，是笔者想要达到的另一个教学目标。于是，笔者决定继续拓展学生的思维，通过创设新的问题情境，将“抬腿法”引入“鸡兔同笼”问题的解决，使学生从中体验到创新思维的乐趣，进一步培养和发展学生的创新意识和能力。

（一）“抬腿法”与“多一原理”在“鸡兔同笼”问题解决中的应用策略

为了拓展学生的解题思路，笔者向学生讲述了“抬腿法”与“多一原理”在“鸡兔同笼”问题解决过程中的妙用：草地上有一群鸡和一群兔。鸡对兔吹嘘道：“我们武艺高强，可以做金鸡独立式。”说着每只鸡都抬起了1只脚，只用1只脚站着。兔子们也不甘示弱地说道：“这有何难，看看我们的兔子作揖。”说罢，每只兔都抬起了2个前肢。这就是“鸡兔同笼”问题中的“抬腿法”。大家可别小看这个“抬腿法”，将它运用在“鸡兔同笼”问题解决过程中，可以大大简化我们的解题步骤。（课件出示“抬腿法”的解题思路，如图3所示。）在“抬腿法”的解题过程中，潜藏着一种“微妙的数量关系”，我们把它取名为“多一原理”。所谓“多一”，指两种同类事物相比较，一种事物所含的部件数量与事物本身的个数相等，而另一种事物的相同部件比其数量“多一”。在这种特殊情况下，用两种事物该部件的总量减去两种事物总量所得的差，就是所含部件比事物本身的数量“多一”的那种事物的个数。例如，用“抬腿法”解决前面的问题，解题过程便可简化如下：先假设每只动物都抬起半数的脚，那落在地上的鸡和兔的总脚数便变成了26÷2=13只脚；13-8=5，这个5就是兔子的只数；有了兔子的只数，剩下的鸡的只数便是8-5=3只了。我们来总结一下：前面的猜测法和画图法都是从动物的只数出发，算术法基于“极端假设”思想直接从腿数入手，“抬腿法”同样是从腿数入手，但因为借用了“抬腿”使腿数减半后两种动物腿数“多一”的原理而有效避免了两种动物身份的转换，巧妙推算出了鸡和兔的只数。

作为一种典型的数学问题解决模型，“鸡兔同笼”问题可广泛运用于解决现实生活中有关两种事物之间的数量关系的比较问题。而这些生活中的问题，在“抬腿”的情况下未必都能刚刚好符合“多一”的情况。比如下面的例题：“田野里有鸡和蝴蝶12只，它们的总腿数是44条腿，请问鸡和蝴蝶各有多少只？”虽然运用“抬腿法”，让鸡和蝴蝶各抬起一半的腿之后，鸡落地的腿数与只数是一一对应关系，但每只蝴蝶落地（或下垂）的腿数则比每只鸡落地的腿数多2条（蝴蝶共有6条腿），此时，用44÷2后可得到22，22-12后得到10，这个10仍然是多出的蝴蝶的腿数，因为鸡的腿数已经全部减掉，那么此时的10条腿不能代表蝴蝶的数量，必须再除以2，运用10÷2=5算出蝴蝶的只数。在该问题的解决过程中，蝴蝶与鸡“抬腿”后的腿数差虽然不是“多一”而是“多二”，但依然可以运用“多一原理”，先排除鸡的腿数，然后算出蝴蝶的只数5，再由蝴蝶只数推算出鸡的只数12-5=7只。也就是说，依此类推，“多一原理”依然可以与“抬腿法”相配合，无论是“多三”“多四”，都可以推算出两种相关事物之间的数量关系。

（二）组织学生灵活运用“抬腿法”和“多一原理”，巧妙解决生活中两种事物之间数量关系比较的现实问题

在现实生活中，符合“多一原理”的问题并不多见，这个时候便需要学生学会灵活變通，人为制造出“多一”的特效，将复杂的数学问题简单化，使较难解决的问题在“多一原理”的支持下迎刃而解。

例如，课堂教学中，笔者出示了下面的例题：30名职工共同制作新年贺卡80张，男职工每人制作3张，女职工每人制作2张，请问男、女职工各几人？

乍一看，这道题的题干里根本不含“多一”的元素，但仔细分析就会发现：如果用贺卡的总张数除以2，女职工的人数和她们制作的贺卡数就相等，男职工每人对应的贺卡张数就由原来的2张缩减至1.5张，在“一人一卡”的基础上，每个男职工就会多出半张，即在一人一卡的基础上，每多出0.5张贺卡，就代表着存在一名男职工。于是，该题的解题过程如下：80÷2=40（张）；40-30=10（张）；10÷0.5=20（名男职工）；30-20=10（名女职工）。

当然，还可以换一种方式运用“多一原理”：第一步不用总贺卡数除以2，而是把每名职工制作新年贺卡的张数都减去1，解答会更简单。如果把每名职工制作新年贺卡的张数都减少1，则：女职工每人制作贺卡1张，贺卡数量和人数形成了一一对应关系；男职工每人制作贺卡2张，制作的新年贺卡数就比人数“多1”，在“一人一卡”的基础上卡数比人数多了几张，就代表着存在几名男职工。解题过程如下：80-30=50（张）；50-30=20（名男职工）；30-20=10（名女职工）。

由上面的例题，可以总结出“多一原理”应用的核心是实现某种事物的数量与其某个部件数量的一一对应，而另一种事物与其某个相同部件的数量既可以“多一”，也可以“多二”“多三”“多四”……实现一一对应的方法，既可以运用除法的方式来制造，也可以运用减法的方式。需要说明的是，在完成“一一对应”关系的制造后，总数一定要随之发生变化：如果用的是除法，总数就要缩小相应的倍数；如果用的是减法，总数也要核减相应的数量，这才是“多一原理”运用中变与不变的核心思想。也就是说，无论现实的情况如何，都可以制造出一个事物的一一对应，但是，大前提是两种事物的某个特定部件在数量上形成了一定的比例关系。条件再次放宽，也就是满足这个条件的问题，都可以转化为“鸡兔同笼”问题。

总之，教师要善于创造机会和平台，引导学生在数学学习的过程中树立创新意识，学会融会贯通，激发思维的灵活性，培养和发展创新思维能力。

参考文献

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022.

作者简介：黄春莲（1979— ），广西博白人，本科，一级教师，主要研究方向为小学数学教育。

（责编 白聪敏）