从静观走向实验
汪燕芬






[摘 要]“长方形和正方形”单元包含认识长方形和正方形的特征、认识周长、周长的计算三块内容。通过梳理学生在学习此单元中存在的概念建立不清晰、周长公式算理不明确和解题思维力不够等问题,提出解决问题的路径——开展数学实验,以数学实验变革学习方式,动态呈现数学知识。
[关键词]数学实验;长方形;正方形
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2023)02-0040-04
苏教版三年级上册“长方形和正方形”这一单元的知识对学生来说较为抽象,因此,笔者先梳理出学生在单元学习中存在的一些普遍性问题,再以一个个具体案例阐述数学实验活动的实施路径,以期帮助学生突破学习难点。
一、问题分析:过度静观,导致学习过于抽象化
本单元的教学主要存在三大问题,究其原因主要是学生只是静听教师讲授知识,静观教师一个人操作,而缺乏动手实践。
1.概念理解不透彻
本单元的教学目标是学生掌握长方形、正方形的基本特征以及周长概念。而理解周长的含义是学生学习的难点,也是后续学习各图形周长计算的起点。对于稍加变式的练习题“如图1,判断是甲的周长长还是乙的周长长”,学生往往判断不准,原因就在于他们对周长的认识不够清晰,容易将周长和图形的面积混淆。这说明三年级的学生对周长概念的理解不透彻,易受干扰,教师要帮助其寻找到有效构建“周长”概念的方式。
2.周长公式算理不明确
长方形周长的计算是对长方形对边相等的特征的综合运用。在多种计算长方形周长的方法中,学生容易掌握的方法有“长方形的周长=长+宽+长+宽”“长方形的周长=长×2+宽×2”,但对“长方形的周长=(长+宽)×2”的方法只会套用公式机械计算,并不明白其中的算理。可见,把“长方形的周长=(长+宽)×2”理解透彻是学生学习的难点。
3.解题思维力不够
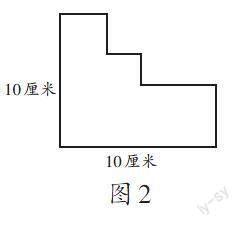
计算周长的变式题很多,例如,求图2中的多边形的周长。解题首先要在深刻理解周长含义的基础上明确是求哪些边线长度的和,然后通过平移,将多边形转化为正方形后才能求出周长,这对学生的思维要求比较高。本单元还有大量需要通过拼或剪图形之后求周长的问题,如“把两个长6厘米、宽4厘米的长方形拼一拼,怎么拼使得周长最长?怎么拼使得周长最短?”“把一个长8厘米、宽6厘米的长方形剪成两个相同的小长方形,两个小长方形的周长之和比原来的长方形的周长最多增加几厘米?”。为此,教师要研究如何帮助三年级的学生来理解并掌握解决这类问题的策略,以发展他们的思维。
二、解决问题的路径:数学实验的开发与实施
学生在学习中如同旁观者,以一种静观的状态来获取知识,这样的学习方式是呆板的。为了优化学生的学习方式,笔者找到了解决问题的路径——开展数学实验。
数学实验是指让学生借助实物和工具,通过对实验素材进行“数学化”的操作来验证数学结论、理解数学概念、探索数学规律、解决数学问题的一种数学学习方式。在2021年,本校成功申报了江阴市专项资金项目“指向学科育人的小学‘数学实验’的实践研究”,在项目研究的引领下,笔者作为该项目的主要参与者,开始和数学实验零距离接触。在教学 “长方形和正方形”单元时,笔者开展数学实验研究,让学生从静观走向实验,有效突破了教学难点,使教学取得了良好的效果。
1.数学实验内容的开发
数学实验活动应具备操作性、实践性和挑战性等特点,笔者从以下三方面来开发本单元的数学实验内容。
第一,教材。在充分理解教材编者意图的基础上,在教材中的新授内容以及习题中开发实验内容。例如,教材三年级上册第38页的习题(如图3)就可重新设计,开发为“从长方形中剪出一个最大的正方形”的实验活动,并用“如何折?”“为什么这样折?”“最大的正方形和长方形之间有什么关系?”等问题引导学生深入思考。
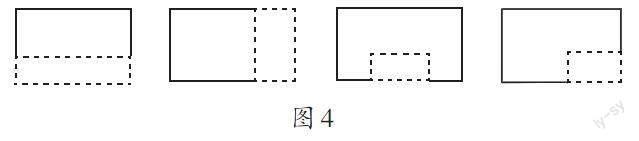
第二,数学课外读物。例如,《亮点给力提优班多维互动空间》(数学三年级上册)(以下简称“亮点给力”)这本数学读物的趣味性、挑战性比较强,如“剪去一个小长方形,周长会怎样?(如图4)”,可开发成数学实验:动手剪一剪,有几种不同的剪法?每种剪法对应的周长发生怎样的变化?综合各种剪法,你得出什么结论?
第三,生活问题。小学数学问题大部分来源于生活问题,教师可把学生要解决的生活问题设计成数学实验。
数学实验1:王大爷想在院子里围一个长10米、宽6米的长方形鸡舍。如果一面靠墙,有几种不同的围法?哪种围法用的篱笆最少?
数学实验2:快过年了,王阿姨有一张长26厘米、宽8厘米的长方形彩纸,她想剪出最大的正方形来制作窗花,一共可以剪出几个最大的正方形?
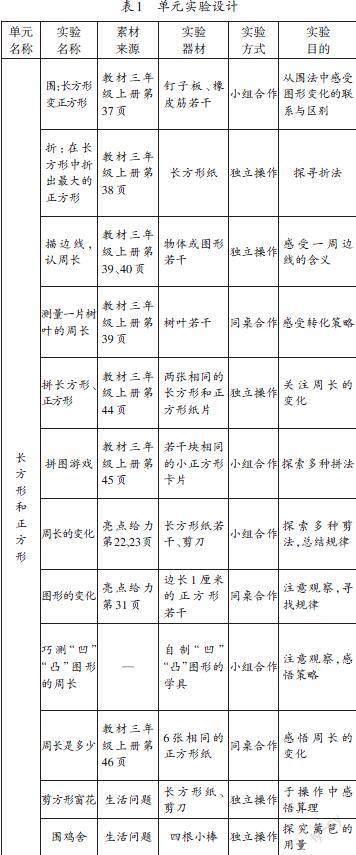
经过生活情境包装的数学实验更加能激发学生学习的乐趣。笔者充分理解教材意图,研读课外数学读本,再结合生活问题,对本单元数学实验进行了个性化和创造性地开发和设计(如表1)。
2.数学实验活动的实施
在本单元学习中,笔者通过开发数学实验,组织学生在活动中变革学习方式,如猜想试验、动手实践、探寻规律、总结归纳,使学生的学习过程留下痕迹,有效解决了文首提出的三个问题。
(1)建立概念:在实验中直观感知,理解数学概念
在教学长方形、正方形的特征时,笔者先让学生猜想边和角有什么特征,然后开展实验,引导学生通过量、折、比来验证自己的猜想。通过互动交流,学生的发现由无序变为有序、由零散变成完整。最后,通过实验“先在钉子板上围一个长方形,再把它改成正方形以及在一张长方形纸中剪出一个最大的正方形”让学生在长方形、正方形特征的比较中感受两者之间的联系,深刻理解两者的特点。
為了避免学生混淆周长和面积,笔者设计了丰富的实验活动:描边线、指边线、围边线等。先让学生用笔描出三张书签一周的边线(初步感知);再让学生分别指出课桌面、数学书封面、三角尺一周的边线(再次感知);最后让学生想办法测出一张树叶的周长。学生在建立周长概念的过程中,都是通过充分操作、实验来感知的。比如教材中的思考题“两个长5厘米、宽2厘米的长方形重叠成一个图形(如图5),求这个图形的周长”,只有让学生动手描边线,才能使学生的思维聚焦到概念中的“图形一周的边线”上。
(2)明晰算理:在实验中丰富表征方式,促进深度理解
数学表征是儿童数学学习的关键能力,也是儿童利用已有经验,在探索未知问题时,构建自己对未知问题理解的外显方式。对于“长方形的周长=(长+宽)×2”,为了帮助学生突破学习难点,笔者设计了数学实验:先用四根小棒搭一个长方形,然后探索如何计算周长。学生经过探索,得出多种方法,其中最典型的三种算法如图6所示,尤其是第③种,学生通过操作小棒,直观感知长方形的周长可以平均分成两份,每一份都是“长+宽”,所以“长方形的周长=(长+宽)×2”。学生在操作中思考,用图示表征算理,这比单独用语言表征、静观教师的图示表征效果好。可见,学生自己做过了,彻底理解了,就不会忘记。
(3)提升思维:在实验中渗透思想方法,促进思维发展
获取数学知识和结论不是数学实验唯一的目的,更重要的是帮助学生经历探究过程,使其在实验过程中获得数学活动经验,提升和发展数学思考力、探究能力和创新能力。
【案例1】化曲为直,测量一片树叶的周长
认识周长后,学生开始学习测量周长,如三角形、四边形、五边形等图形的周长,只要用直尺测量,再计算,就能解决。但生活中有大量曲线围成的图形,如何测量它的周长呢?笔者组织学生开展“测量一片树叶的周长”的实验。学生经过讨论后,有的说把树叶当成一个近似的长方形去测量,有的说把叶子的边线先剥离下来,有的说用尺子一段一段去量……“有没有既方便量,又量得准的方法呢?”笔者的这个问题一出,学生再次商讨,最后定为先用一根细绳沿着树叶边缘围一圈,再把绳子拉直后用尺子量。当进行实验反思时,笔者以问题“通过这个实验,你学会了哪一种测量方法?”引导学生反思与小结,渗透“化曲为直”的思想。
【案例2】平移转化,巧求图形周长
例如,图7的第二和第三个图形,如何计算它们的周长?笔者先引导学生用磁力棒围出这两个图形,接着提问:“如何求这两个不规则图形的周长?”学生开始是测量每一条边的长度,后来通过移动磁力棒,把图形转化成了一个长方形,最终顺利解决问题。再如,求图8中凹凸两种图形的周长。学生也是通过移动小棒,将其转化为规则图形后再求周长。
在实验反思环节,笔者追问:“通过这个实验,你学会了哪一种思考方法?”学生异口同声回答:“轉化法。”可见,学生亲身体验了图形的转化,已学会了把不规则图形转化成规则图形来解决问题的方法,并把这种方法铭记于心。
【案例3】有序列举,理解图形构造的规律
如图9,正方形的边长为1厘米,正方形的数量与拼成图形的周长之间有什么样的关系?
学生要完全理解这道题,就要进行数学实验,经历图形的构造过程。实验前,学生讨论出先用小棒摆或者用笔画出图形,从数量是1个正方形开始研究,再研究2个正方形相拼、3个正方形相拼……确定实验步骤后,学生一边摆或画,一边找关系:1个正方形的周长是4厘米,2个正方形相拼的周长是6厘米,3个正方形相拼的周长是8厘米,4个正方形周长是10厘米……学生用有序列举的方法边实验边思考,最终发现规律:每增加一个正方形,周长就增加2厘米(增加2条边长),即“第n个图形的周长=2×n+2”。
数学实验,不是仅仅停留在“做”的表层,而是注重引导学生在“做”中思,只有做思结合,才能促使学生真正掌握解决问题的策略,体会数学思想方法。
综上,依托数学实验,以发展思维为内涵,使静态的数学知识动态化,这样不但能有效帮助学生突破学习难点,还能在促进学生对数学知识深度理解的同时发展学生的数学思维。
[ 参 考 文 献 ]
[1] 施良方,崔允漷.教学理论:课堂教学的原理、策略与研究[M].上海:华东师范大学出版社,1998.
[2] 沈艳.课堂教学的改革与创新[M].南宁:漓江出版社,2010.
[3] 董林伟.“做数学”:中小学生适合教育的实践构建[J].教育研究与评论,2021,(3):16-21.
[4] 郭庆松.在“做数学”中促进深度理解[J].教育研究与评论,2021(3):30-35.
(责编 覃小慧)

