深度学习理念下的小学数学错题评讲教学策略

黄毕年

错题评讲是学生主动反思调整、重构认知的一种学习历程。以深度学习理论为指导，探索总结“活动评讲增体验”“联想评讲建结构”“变式评讲触本质”“迁移评讲助应用”等教学策略，构建错题评讲教学的新样态，可助力“减负提质”真正落地。错题评讲不应是教师简单评讲错题，学生更正答案，而应是学生参与错题评讲活动并在其中再次反省调整、重构认知的一种学习历程。教师面对学生在学习中出现的错题，该如何评讲才能让学生“迷途知返”，不再出现“评讲过仍又错”的窘境，对当前“减负提质”课题有很强的实践意义。深度学习作为近年来引领小学教学改革的重要理论，是数学错题评讲教学的指导思想和理念支撑。笔者基于深度学习理念，突破传统“师讲生纠”低效化错题评讲模式，创新小学数学错题评讲策略。

一、活动评讲增体验

深度学习提出“活动与体验”的学习机制，强调引导学生全身心投入参与到数学活动中，引发学生积极从事数学思考，获得鲜明、深刻的数学体验。这里的活动，不只是外在的肢体参与，更为重要的是内在的数学思维活动。在数学错题评讲教学中，之所以不少学生简单、肤浅参与，很大程度上是由于教师侧重于自己的充分讲解，认为讲明白了学生就知错并能改正了，而忽略了学生是否主动投入参与其中。事实上，“解铃还须系铃人”，数学错题评讲主体应是学生。错题评讲中，应让学生有活动的机会，有亲身经历错题的发现、纠正、调整与完善的机会。

首先，深度学习是指“深”在人的心里，“深”在人的精神境界中。错题评讲中，学生的主动学习愿望不是自发的，而是需要教师唤醒与点燃的。因此，错题评讲中教师应重视创设有温度的活动，变教师讲为学生做，让学生经历遇见错题、发现错题、分析错题及纠正错题的过程，增强数学活动体验，促进学生主动调适与完善数学认知结构。

例如，在教学人教版数学教材四年级上册“商不变规律”的简算时，教师呈现如下关于1700÷500的三道练习题目，让学生思考。

“下列简算对吗？你是怎样发现的？”

（1）1700÷500=3……200；

（2）1700÷500=17÷5=3……2；

（3）1700÷500=（1700÷5）÷（500÷5）=340÷100=3……40。

教师主动让位，学生通过“被除数=除数×商+余数”的数量关系计算、验证，发现（1）是正确的，而（2）和（3）错误的。这是为什么呢？学生产生释疑的欲望，展开思辨与交流、比较与分析、思考与判断，认识到被除数与除数同时乘以或除以不为零的相同数，虽然商不变，但是余数也发生了与被除数、除数相一致的变化。所以（2）和（3）简算中的余数，应根据简便算式中被除数、除数的变化倍数逆向推理求得余數应为200。这里，教师呈现学生的典型解法，以生探代师讲，引导学生主动参与发现、探索与解决问题的过程，获取鲜明的数学活动体验，不仅纠正数学错题，而且让学生学会交流与表达，增强数学活动体验，获得学力生长。

其次，深度学习具有高起点的特点。学生亲身经历与活动体验，并非完全是原生态的创造过程，而是有结构、简约地经历“再创造”过程。所以，错题评讲教学中，学生的“亲身经历”活动仍离不开教师的适时介入与指导。

例如，在教学人教版数学教材二年级下册的“轴对称图形”时，学生往往会产生“平行四边形是轴对称图形”“一般长方形有四条对称轴”等错误认知。在错题评讲时，既不能靠教师的讲解与强调，也不应是让学生随意判断，而应是教师适时指导学生实践与体验，经历关键环节的“再创造”过程。教师在学生争执不下、迷惑不解时，引导学生动手折、动眼看、动脑想后，再作出交流与判断。这样，学生在教师指导下适时经历关于轴对称图形判断的“再创造”过程，获取丰富的数学体验，重构属于他们的数学知识体系。

二、联想评讲建结构

深度学习强调“联想与结构”，提出经验与知识之间相互转化的学习新样态，即应将当下的学习内容与学生已有经验关联起来，融入学生原有的认知结构中，丰富和固定知识的检索与提取方式，拓展学生的认知结构。错题评讲中，教师若就错讲错，知识点就会呈现零碎、点状、割裂状态，缺乏整体性与结构化，只见树木，不见树林，学生侧重于个别识记，无法整体把握，自然评讲效果低下。深度学习视角下的错题评讲，将错题置于学生已有的数学经验与结构的整体关联之中，强调用学生的个体经验来关联错题学习，同时以错题重构的新结构进一步反省与完善已有的数学经验，实现两者的共生共长，彰显整体教学力量。

首先，深度学习强调的“联想与结构”表现为“以联想引结构”，即借助已有经验进行联想，使所学知识转化成有关联和可操作和思考的对象。错题评讲教学要基于错题的特点，充分挖掘数与数、数与形、数与事等诸多潜在关联，从特定的角度选择与切入，使学生以融会贯通的方式参与错题评讲学习，建立有结构的系统，并在结构系统中显示它的意义。

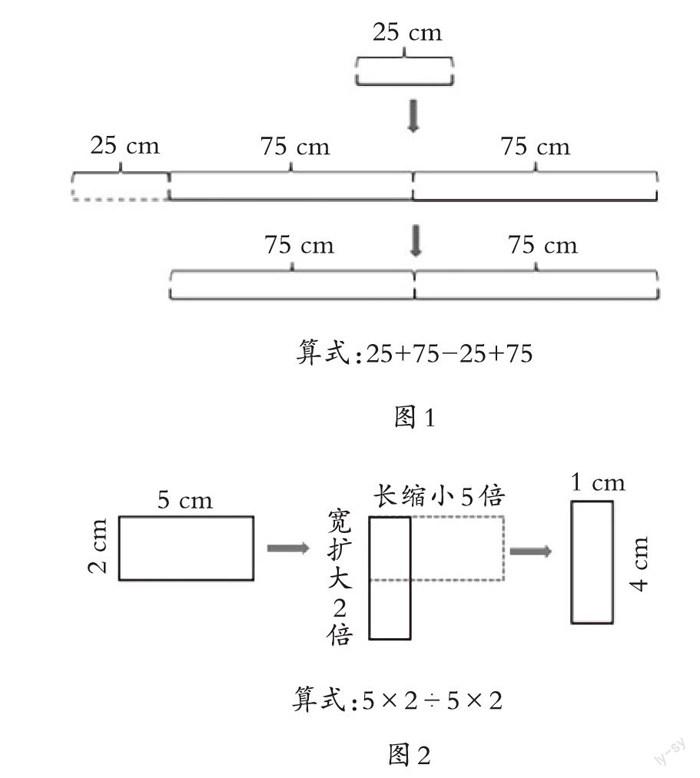
例如，在学生简算中我发现，不少学生的作业出现“25+75-25+75=100-100=0” “5× 2÷5×2=10÷10=1”等错误。有的教师就题讲题，费尽心思，但仍有学生一错再错，这很大程度上是因为教师没有将错题评讲与学生已有经验关联所致。相反，教师抓住“数的加减算式反映线段的长短变化、数的乘除算式反映长方形面积的大小变化”的数形经验，遵循学生直观思维占优势的经验特点，借形析算，讲好算式蕴含的数学故事，就能有效突破学生认知盲点。教师可引导学生根据“25+75-25+75”看式想图（如图1）：一条长25厘米的线段，再增加75厘米，然后去掉25厘米，最后再增加75厘米，不难看出这条线段最后长度是75+75=150（厘米）。“5× 2÷5×2”讲述了长方形面积变化（如图2）：一个长是5厘米，宽是2厘米的长方形，长缩小5倍，宽扩大2倍后，成了一个长1厘米，宽4厘米的长方形，面积是1×4=4（平方厘米）。这样，从数形关联入手，以形释算，轻松明理，发展学生的几何直观素养，使学生牢固建立数学认知结构。

其次，深度学习强调的“联想与结构”，还表现为“以结构助联想”，即运用重建后的认知结构进一步丰富学生已有的经验，形成有意义关联，完善其认知结构。学生答题之所以会错，很重要的一个原因是先前经验的负迁移所致。在错题评讲中，学生运用评讲重构的新认知开展回顾性链接，反省、审视、改造先前的经验，促进认知分化，培养思维的深刻性、思辨性。

例如，在学习人教版数学教材六年级上册的“求一个数比另一个数多（少）百分之几”时，学生往往会出现“一件衣服先提价10%，再降价10%，现价与原价相等”的错误认知。评讲时，在学生明理纠错后，教师还应让学生回顾：“当判断失误时，你是怎么想的？是受到什么影响所致？”“‘一个数增加百分之几再减少百分之几’与‘一个数增加几再减少几’的数量关系相同吗？”进一步引导学生明辨是非，厘清前者的数量变化是相对的，而后者是绝对的。所以，两者表示的数学意义是不同的。这样学生就拓展了对两个数量的认识，体现了“联想与结构”是相互成就、相互转化的一致性，培养了学生系统化思维能力。

三、变式评讲触本质

深度学习强调“变式与本质”，是指学生通过变式对学习材料对象进行深度加工，触及并把握事物的本质，排除非本质的干扰，形成清晰的基本概念。在错题评讲中，之所以会发生“都讲过仍又错”窘境，很大程度上是由于教师的错题评讲不得法，重于单一正例评讲，轻于结构变式评讲，导致学生对错题的思辨如同蜻蜓点水，隔靴搔痒，未能触及数学问题的本质所在。因此，错题评讲中教师应紧扣数学内容本质，迂回侧击，变式评讲，引领学生变换角度识错 、纠错，让学生在变中求不变，彰显数学本质，收到正面教学无法达到的效果。

首先，把握事物的本质，才能以简驭繁，举一反三，闻一知十。错题评讲中教师要充分利用错题资源讲清道理，帮助学生由表及里，把握知识的内在联系和学科本质，进而由本质走向变式。

例如，在教学人教版《义务教育教科书·数学》四年级下册“乘法分配律简算”时，不少学生出现了形如“101×17=17×100+1”“99×99+1=（99+1）×99”的错误。有的教师仅强调运用乘法分配律简算的注意方法，可学生仍一错再错，其重要错因是学生只停留于识记层面，没有对乘法分配律的核心概念进行本质性理解。事实上，纵析知识联系可知，四年级所学的乘法分配律是二年级乘法意义的拓展。因此，在评讲错题时，教师不仅要强调算法，更应强化算理，要侧重于从乘法意义的角度帮助学生识错与纠错。从左往右观察第一个错式可知，101×17表示101个17可以拆成100个17的和加上1个17的和，而非加上1，所以101×17=17×100+1×17；同理，第二个错式中“99×99+1”表示99个99的和加上1，并非表示100个99的和，正确算式应为99×99+1×99=（99+1）×99。这样，引导学生从乘法意义的“大概念”出发去评析乘法分配律的错误简算，学生对运算律本质的理解就更深透，也就更有利于学生迁移与变式，培养学生灵活的思维能力。

其次，深度学习认为，事物本质蕴含于正例的材料中，但不易为小学生所感知与发现。因此，在错题评讲中，教师适时借助正例与变式的比较，形成结构化素材，可以促进学生对错题的深加工，使其把握数学错题的错因所在，凸显数学本质。

例如，在教学人教版数学教材五年级下册“求一个数是另一个数的几分之几”时，在“一个小队有男生12人，女生比男生多4人，男生占全班的几分之几？”的练习中，不少学生列出了4÷12、12÷（4+12）、4÷（4+12）等错误算式。如果教师仅作正面讲解，强调审题认真、遵循公式、加强验算等注意事项，学生往往不以為然，难以达到有效纠错的目的。教学中，我变换角度作评讲，先以式构题：“如果要使上述列式正确，原题的数学信息该怎样修改？” 引导学生以式探因，逆向思考，进一步明晰错误算式的问题背景：“4÷12表示是女生比男生多的人数占男生几分之几？12÷（4+12）表示男生是女生的几分之几？4÷（4+12）表示女生比男生多的人数占女生的几分之几？”再以式引思：“纵观以上错误，你认为要求解答一个数占另一个数的几分之几时要注意什么？”进一步引导学生明晰：提炼解题的数量关系和基本路径，都是要先求出一个数和另一个数，再用除法列式计算，用分数表示两数相除商的结果。这样变换角度评讲，体现了深度学习“变式与本质”的内涵特征，增强了学生对数学问题本质的把握，有利于学生举一反三、触类旁通。

四、迁移评讲助应用

深度学习强调“迁移与应用”的活动特征，提出模拟社会实践，倡导间接经验直接化，体现了用数学语言表达现实世界的数学核心素养，要求将所学知识转化为综合实践能力。有学习就有迁移，迁移是学习的出发和归宿。数学是现实生活的抽象，而现实是抽象数学的具体。在数学错题评讲中，教师应引导学生跳出数学学习的狭隘框框，不直接在数学领域评讲错题的对错及理由，而是将学习内容外化、迁移、放置到具体生活中加以观察、表征与思考，这样有利于学生另辟蹊径，从实践运用角度对错题加以反思与调适，思考得更独特、更灵活、更深刻，引发高阶思维的真正发生。

首先，“迁移与应用”强调对学习内容的具体外化，是学习结果的操作与实践，是知识活化的重要标志。错题评讲要跳出用数学评析数学的范畴，从生活应用的角度思考数学，这样的数学思考就能更深入、更灵活。

例如，在教学人教版数学教材五年级下册“长方体表面积”时，一位教师出示如下一道题目：一个长方形游泳池，长60米，宽40米，深3米，要粉刷这个泳池，需要粉刷多少平方米？有的学生列式为（60×40+40×3+60×3）×2=5400（平方米）。教师引导学生联系游泳池上面露天的实际情形可知，不需求长方形泳池六个面的表面积，只需求出五个面的总表积即可，所以列式为60×40+40×3×2+60×3×2=3000（平方米）。教师进而引导学生思考：“联系日常生活情形，在解答有关长方体总面积数学问题时，还有哪些情形不需要求得六个面的表面积？”学生纷纷畅所欲言，各抒己见，提出众多想法，如“要求长方体鱼缸的玻璃面积时，也是往往只需考虑长方体五个面面积即可”“粉刷教室的墙壁，只需四个侧面面积之和和一个顶面面积外，还需扣除门窗的面积”“要求长方形通风管的材料面积是多少时，只需求出四个侧面面积之和”等。这里，教师将错题迁移到具体生活实践中进行评析，不仅让学生的数学思维更加有形、具体、可视，而且丰富、复杂的现实生活，为错题辨析提供了具体的背景和开放的思路，有利于学生深度理解错因，重构正确认知，培养了学生灵活解题能力和实践能力。

其次，“迁移与应用”不只是检验、判断学习结果的方式，更是重要的学习理念与具体方式。错题评讲中，教师要引导学生养成“由数到事”的自觉意识，主动形成将数学问题迁移到具体生活背景中考查与思考迁移能力，让错题评讲有丰沃的土壤和深厚的根基。

例如，在学习人教版数学教材四年级上册“商不变规律时”时，在练习中出现形如“△÷12=2，那么（△×5）÷12=2÷5；100÷△=5，那么（100×5）÷（△×5）=（5×5）”的错误判断，反映了学生对商不变规律理解得不透彻。为此，教师可引导学生联系生活实践经验帮助学生理解，对于第一个错式可这样思考：一堆馒头平均分给12人，每人得2个。后来馒头的数量扩大5倍，仍平均分给12人，那么每人得到的数量应更多了，不是“2÷5”，而是“2×5”，即每人得到馒头数量是原来的5倍。同理，第二个错式的辨析，也可迁移至具体的分东西情境中加以识别、判断，重构正确判断：100÷△=5，那么（100×5）÷（△×5）=5。

教师这样进行错题评讲，能够进一步增强数与事之间的联系，让错题辨析更加生动、形象，学生的建构也愈加牢固，彰显了迁移与应用的力量。

课题项目：本文系福建省基础教育课程教学研究课题“‘双减’政策下小学数学错题资源开发与利用的实践研究” 阶段研究成果。课题编号：MJYKT2021-050。

（责任编辑：杨强）