太赫兹大规模MIMO中结合量子变分算法的预编码方案*
汪锐,李汀,解培中
(南京邮电大学通信与信息工程学院,江苏 南京 210003)
0 引言
太赫兹和大规模MIMO技术是当前5G和面向6G通信的关键技术。太赫兹通信具有大带宽和传输速率高等特点,面向太赫兹频段的通信技术有望解决当前无线通信系统频谱稀缺和容量限制的问题。大规模MIMO技术是对第四代无线通信技术中的MIMO技术的延伸,它从空间上提升了系统容量,提高了通信系统的性能。但随着大规模MIMO中天线数的增大,算法复杂度以及实现的困难程度也会大幅增大,对于研究如何降低算法复杂度和如何减少开销是当下研究的重点。另一方面,量子计算与机器学习的结合成为新的交叉研究领域。量子计算由于其高并行性,n个量子比特能够计算传统通信中2n维的矩阵,能够大大降低传统机器学习算法的复杂度,在目前中等规模的含噪量子计算机上,可以接近传统算法的性能。因此,结合量子机器学习的无线通信技术将逐渐成为基于人工智能的6G无线通信研究的一个可能关注点。本文创新性地提出将量子机器学习应用于太赫兹大规模MIMO系统的预编码设计中,探索人工智能与6G通信具体技术环节结合的新方式。
在MIMO系统中,为了抑制信号干扰的影响,预编码技术成为解决问题的关键。预编码方案通常分为两种:全数字预编码和混合预编码。全数字预编码可以同时控制传输信号的相位和幅度,在单用户系统和多用户系统中都可以使用。根据处理方式是否线性,可以将全数字预编码划分为线性预编码和非线性预编码。线性预编码包括匹配滤波(MF)、奇异值分解(SVD)、迫零预编码(ZF)、最小均方误差预编码(MMSE)等。非线性预编码主要有脏纸编码(DPC)[1]、和汤姆林森-哈拉希玛预编码(THP)[2]。在大规模MIMO系统中,混合预编码受到广泛的关注。在单用户系统中,文献[3]提出了空间稀疏混合预编码器,文献[4]提出了基于连续干扰消除的混合预编码器。对于多用户系统,文献[5]提出了将正交匹配追踪(OMP,Orthogonal Matching Pursuit)算法用在基于量化码本的设计方案中,设计了一种混合最小均方误差(MMSE,Minimum Mean Square Error)预编码器,针对用户较多的应用场景,有一定的性能优势。文献[6]提出一种高效简单的混合预编码算法,它直接选用理想数字预编码的相位作为模拟预编码,数字预编码则采用最小二乘法(LS,Least Square)。除了以上这些需要完美CSI的方法,也有一些不需要完美CSI的预编码方法,如一种有限反馈法[8]就是利用毫米波信道模型特点,在一个有限的候选码字集中匹配到相对最佳的码字作为模拟预编码。
目前的量子计算机只支持有限数量物理量子位和有限门保真度,一般的量子算法很难在量子计算机上实现。因此,量子计算发展的一个重要方向就是找到一种可以在有噪声的中型量子计算机上(NISQ,Noisy Intermediate-Scale Quantum)有效运行的算法。量子变分算法(VQA,Variational Quantum Algorithm)可以在依赖外部参数的浅层量子电路中实现。它们也被称作参数化量子电路或量子神经网络(QNN,Quantum Neural Network),量子网络参数可以采用机器学习中的梯度算法在经典计算机上进行优化。近些年来,很多基于量子神经网络的量子变分算法相继被提出,文献[9]提出变分量子本征求解器(VQE,Variational Quantum Eigensolver),一种用于获得给定哈密顿量近似基态的变分算法,经过数值模拟,与传统求解矩阵特征值的算法相比,VQE在求解大维度矩阵的特征值时效率更高,并且能够在NISQ设备上运行。文献[10]针对NISQ设备上变分混合量子经典算法(VHQCA)在解决复杂问题时量子态制备和测量次数过多的问题,提出了一种新颖的优化器。文献[11]将量子变分算法用于求解线性方程组和矩阵向量乘法中的应用,并进行了数值测试。文献[12]提出引入量子奇异值估计算法来求解线性方程组,利用奇异值的变分原理设计一个新的损失函数,训练两个量子神经网络来学习奇异向量并输出相应的奇异值。文献[13]提出一个变分量子线路,来产生二分纯态的奇异值分解。文献[14]提出了一种由标准量子门组成的量子电路来实现梯度优化算法,并在四量子比特系统中展示了齐次多项式优化问题的求解,证明了该算法能够有效解决高维的优化问题。此外,不同于可容错量子计算机对纠错的较高要求,在低深度量子线路实现的量子计算机上噪声能够得到有效的抑制,同时也表明量子计算在有噪声的中等规模量子计算机上运行有一定的可行性。
随着量子技术的不断发展,各大商业巨头、学术机构以及政府战略都将目光转向量子计算,并且作为未来几十年主要的发展方向。同时,随着无线通信技术的快速发展,无线用户的数量规模越来越大,对处理数据的能力和对数据分析的能力需求更高,而量子计算具有的高并行性可以降低传统机器学习算法的复杂度,能够大量减少运算量。因此,将量子计算应用到无线通信领域被认为是助力未来6G、后6G时代无线通信技术发展的一个很有前景的方向。文献[15]设计了一种改进的量子算法用于实现基于MMSE的大规模MIMO上行链路检测,在该问题中,首先设计一个基于量子奇异值估计的量子算法得到量子态形式的发射信号,然后,提出改善的量子态信息提取算法获取量子态发射信号的幅度和相位,以便信息可在传统设备中使用。文献[16]提出一套完整的量子算法用于实现无线通信系统中的多信号分类问题。包括量子奇异值分解的量子信号协方差矩阵重构、基于变分量子算法的密度矩阵特征分解。该量子算法相比于传统的MUSIC算法能够提供多项式甚至指数级别的加速。文献[17]提出基于量子奇异值估计算法的量子ELM算法,将量子奇异值估计算法引入无线信道预测中,将经典ELM算法同量子奇异值估计算法相结合,在伪逆计算的部分使用量子奇异值估计,降低了经典ELM算法的时间复杂度。然而,在太赫兹移动通信系统的预编码技术中,目前还没有同量子机器学习结合的方案,本文创新性地提出将量子变分算法用于太赫兹大规模MIMO系统中的预编码方案的设计中,并在Google量子机器学习平台进行了实验仿真,利用量子计算的高并行性,降低算法的复杂度,提高整个通信系统的性能。
1 信道模型与问题描述
1.1 太赫兹信道模型
太赫兹通信具有大带宽和传输速率高等特点,在自由空间中传播时损耗非常大,且视线路径(LoS,Line of Sight)相对于非视线路径(NLoS,None Line of Sight)损耗较低。本文中,根据文献[18]的描述,太赫兹大规模MIMO信道模型考虑在经典的S-V信道模型(Saleh-Valenzuela)中进行改进,采用归一化线性阵列(ULA,Uniform Linear Array)建模。由于太赫兹信号受到大气吸收、衍射损耗等因素的影响,随着传播距离的增加而衰减很快,因此太赫兹系统中水平和垂直到达角较小。假设每一条传播路径中仅有一条散射路径,这样可以将太赫兹信道视作视距传播信道。则其收发端之间Nt×Nr的时域信道矩阵可表示为:
其中,Nt为基站的发送天线数,Nr为用户接收天线数。L表示传输路径数,αl表示第l条路径的增益,服从复高斯分布,其中,复信道增益满足条件表示归一化常数。δ(•)表示脉冲响应函数,τl表示第l条路径的延迟,Gt,l、Gr,l分别表示发送端和接收端的天线增益,取决于阵列天线的规模以及单个元件的天线阵列函数。φl表示第l条路径的到达角(AoD,Angle of Departure),φl表示第l条路径的离开角(AoA,Angle of Arrival),且分别表示接收端和发送端的阵列响应矢量,可表示为:
其中,λ表示传输信号的波长,d表示天线之间的距离。
1.2 问题描述
图1展示了大规模MIMO系统模型,发送端配备了Nt根天线,接收端配备Nr根天线,发送符号数为d,发送端预编码矩阵为F∈CNt×d。接收端接收矩阵为W∈CNr×d。信道矩阵为H∈CNr×Nt。

图1 大规模MIMO系统模型
为了简化分析,假设发送符号数、发送天线数和接收天线数相等,即d=Nt=Nr。发送端发送的信号可以表示为:
其中,n表示加性复高斯白噪声向量,均值为0,方差为σ2,经过接受矩阵W处理后的信号可表示为:
在大规模MIMO系统中,本文为简化接收端处理,假设WHW=1,系统可达和速率可以表示为:
其中,记Mm=HmHm,Mm的SVD分解为,最大特征向量即为最优解,本文考虑构造一个变分量子系统,将M作为系统哈密顿量,通过量子本征求解器,获得M的最大本征向量,即最大特征向量Vm,式(11)的最优解为fn,由此可以得到预编码矩阵
2 基于量子变分算法的预编码设计
2.1 变分量子特征值求解器
变分量子特征值求解器算法是基于变分原理所提出的,变分原理是指对于任意一个初态用某一体系的哈密顿量作用它时,可以得到该体系在这一状态下的平均能量E,它将大于或接近于体系的基态能量E0,即:
从上式可以看出,如果所制备的初态正好就是体系的基态,那么E=E0,直接得到体系的基态能量;但往往所制备的初态与体系的基态能量有很大的差别,导致E≫E0,这个时候需要引入一组参数,通过不断调节参数,设置一个阈值,使得所制备的量子态能够无限接近于体系的基态。对于一个n阶较大方阵的特征值λ1λ2...λn求解,可以利用VQE算法,寻找到描述某一体系的哈密顿量的本征值E1E2...En,从而获得特征向量。VQE算法的基本流程如图2所示:

图2 VQE算法的基本流程
变分量子特征值求解器是一种量子-经典混合算法,用于寻找体系的基态,并且能够有效地找出一个较大矩阵H的特征值,该算法能够大大降低相干时间的要求。所以,为了求解前文公式(13)的预编码优化问题,本文提出将VQE与预编码结合的算法,将Mm作为变分量子本征值求解器的系统哈密顿量,首先,构建参数化量子线路用于表征可通过参数调整的预编码向量;然后将Mm分解为由泡利矩阵组成的子哈密顿量,分别在量子神经网络中进行训练,经过梯度优化算法,得到最大奇异向量,最终生成预编码矩阵F。
2.2 量子系统哈密顿量Mm的分解形式
在进行量子模拟时,为了能够在量子线路中将哈密顿量成功映射到量子比特上,需要将哈密顿量分解为泡利算符组成的形式。一般地,对于任意一个哈密顿量都可以表示为:
根据上式,可以将式(11)展开成以下形式:
考虑写成相对于系统大小的多项式的哈密顿量,可以近似为n倍张量积之和的矩阵。通过经典加法器,〈H〉的计算简化为一个量子态|ψ〉的简单泡利算子的期望值的多项式数之和,再乘以一些实常数。量子设备可以有效地得到任意数量的简单泡利算子的张量积的期望值。使用n量子位,就可以得到这个2n×2n哈密顿量的期望值。
2.3 参数化量子神经网络的训练
酉算子H表示可观测量的特征值问题,本文提出的算法中,首先要制备预编码向量的参数化量子初态,通过对一个全0量子态|ψ〉作用含参量子线路,如式(15),制备预编码向量对应的参数化量子初态,它可以写成本征态的组合。
实现VQE过程中,首先需要设计搭建量子神经网络QNN,也可以理解为一个参数化量子线路U(θ),来构建试探波函数使得U(θ)|ψ〉=|ψ(θ)〉。量子神经网络U(θ)如图3所示。其中D表示量子神经网络的深度。

图3 量子神经网络
通过作用量子神经网络U(θ)在初始态上,得到输出态。在VQE模型中,通过给出解析表达式来计算全局损失函数L(θ)的梯度,并且可以通过更新参数化量子线路中的参数θ来估计梯度。损失函数L的梯度取决于参数θ,把期望值作为优化的损失函数,一般由关于哈密顿量的期望值给出。
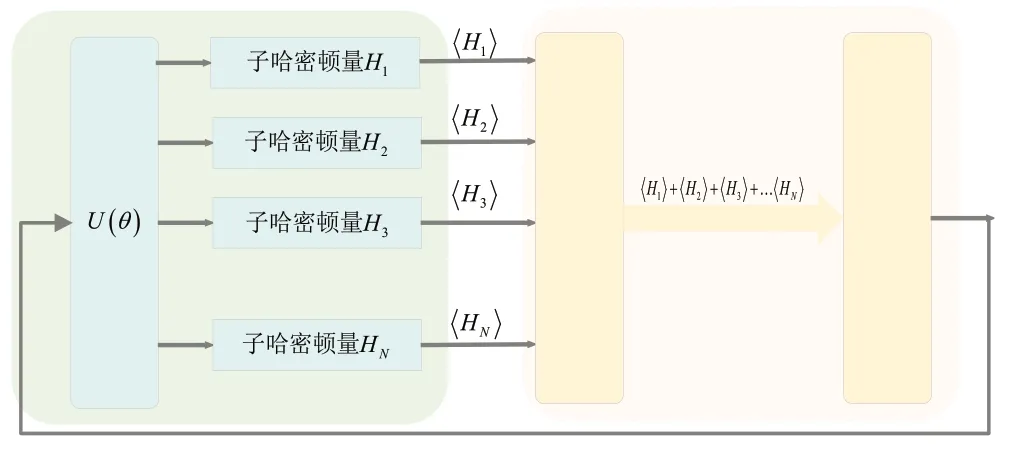
图4 量子变分算法流程图
整体算法步骤如下:
步骤1:根据Saleh-Valenzuela信道模型生成信道矩阵,以系统可达和速度最大为目标,将最优预编码矩阵设计问题转化为的特征分解;
步骤4:随后构建参数化量子神经网络,将分解后的子哈密顿量加载到参数化量子线路中进行训练。得到输出态|ψ(θ);
步骤5:根据步骤二中经训练后得到的输出态中的参数θ,将期望值作为优化的损失函数,损失函数如式(17)所示;
步骤7:根据训练完成的量子线路U(θ),提取对应的矩阵表达式,提取最大本征态对应的最大本征向量Vm,fn=Vm;
步骤8:依次计算{f1,f2,...fN},生成预编码矩阵Fopt=diag{f1,f2,...}。
2.4 算法复杂度分析
一般使用经典计算机时,需要分别优化哈密顿量的所有子哈密顿量,这会受到N表示性问题的影响,对应量子复杂度类为QMA,这对于经典计算机和量子计算机来说都是难以解决的。本文提出的方案的优势在于,根据量子计算的高并行性,量子硬件可以存储全局量子状态,其资源比经典硬件所需的资源要少得多,因此不会出现N表示性问题。
任意数量泡利算子的张量积的期望值可以通过每个量子比特的局部测量来估计。这种独立的测量可以并行执行,从而产生恒定的时间成本[19]。此外,这些算子中的每一个频谱都是有界的,每个算子的复杂度可以由计算精度p来描述,复杂度可以近似估计为。这里的M是哈密顿量分解中的项数,hmax是哈密顿量分解中具有最大范数的系数。这种方法的优点是准备状态后进行单次测量的相干时间为。相反,这种方法相对于量子期望估计的不同是操作总数的缩放,这种缩放反映所需状态准备的重复次数,在量子期望估计中,状态准备步骤的次数是恒定的。从本质上讲,通过增加关于量子期望估计的多项式重复次数,显著降低了相干时间要求,同时保持了相对于经典情况的指数优势。此外,量子变分特征求解器对基态波函数近似计算基态特征值时,相对于量子期望估计算法,同样具有相对短的相干演化的优势。
本文提出的算法与经典算法相比,算法复杂度有显著的优势。使用当前已知的量子态精确编码存储量子态向量需要至少2n个复数。给定这种量子态,使用经典算法计算期望值需要点运算。因此,当在经典计算机上执行单个函数评估时,预计在存储和计算中都需要指数级资源。此外,经典最小化算法准确表示此状态所需要的参数数量为2n。因此,即使执行经典最小化算法来确定也需要指数级的资源。可以粗略估计这个过程的复杂度为。可以发现,与经典算法相比,本文提出的算法在复杂度上有显著的优势。
3 数值仿真
本文采用的仿真环境为太赫兹大规模MIMO系统模型,训练参数设置为:量子神经网络深度D设置为2,总迭代次数设置为80。为了验证算法的有效性,在Google量子平台进行验证,利用量子编程框架cirq,分别与以下算法在不同信噪比和不同发送天线数下的系统可达和速率进行对比:1)SVD预编码;2)MMSE预编码。由于目前在经典计算机中模拟量子计算机是一个困难的问题,量子计算系统的操作行为需要经典计算机中指数数量的操作来模拟,因此本文的仿真实验在接收天线数较少的情况下进行。仿真结果如图所示。
图5和图6分别表示当系统为Nt=4、Nr=4时和Nt=16、Nr=16时各算法系统可达和速率和信噪比的关系,从图5和图6中可以看出,系统可达和速率随信噪比的增加而增加,本文提出的算法系统可达和速率性能近似于传统SVD预编码性能,优于MMSE预编码性能。

图5 4×4时不同信噪比下系统可达和速率对比图

图6 16×16时不同信噪比下系统可达和速率对比图
图7表示当Nr=4时各算法系统可达和速率随着发送天线数由16到196的变化关系,由图7中可以看出,各算法系统可达和速率随发送天线数的增加而增加,本文提出的算法性能与SVD预编码算法性能相近,优于MMSE预编码算法。

图7 发送天线数由16到196的系统可达和速率对比图
4 结束语
本文提出的结合变分量子本征值求解器的预编码方案,以系统可达和速率最大为目标,利用变分量子特征值求解器,将问题转化为求解系统哈密顿量的期望及其对应的量子态,在量子机器学习平台上准备一个参数化的试探波函数,然后结合经典机器学习的优化算法,训练得到一组最优的参数来更新参数化量子线路,从而获得最优的预编码矩阵。经验证分析,该方案能具有指数级加速,与经典的算法相比较,性能相近,但具有计算复杂度优势。本文提出的方案是将量子机器学习与无线通信技术相结合的一次尝试,为未来无线通信技术的发展提供了更多的可能。

