基于Apriori算法的沿海地区洪涝灾害成因分析
吴嘉欣,林凯荣,2,3,刘梅先,2,3,黄利燕
(1.中山大学 土木工程学院,广东 珠海 519082; 2.广东省海洋土木工程重点实验室,广东 珠海 519082;3.广东省华南地区水安全调控工程技术研究中心,广东 珠海 519082)
0 引 言
近几十年以来,随着全球气候变化以及不断加快的城镇化进程,城市洪涝灾害愈加频繁,造成了巨大损失[1,2]。因此,研究城市洪涝灾害的成灾机理以及相关防灾减灾技术,在当前气候与城镇变化条件下显得尤为重要。目前,评估洪涝灾害的方法主要包括物理模型、数值模型和经验方法[3]。物理模型运算复杂且需要大量观测数据验证,在应用中受到较大的限制[4],数值模型则可通过大量水文、地形等数据来模拟实际过程,因此很大程度上已取代物理模型[5],随着GIS和遥感的发展,经验模型开始应用于在洪涝灾害评价中[6]。定量的方法依赖于数据,定性的方法受限于专家,半定量的多准则决策方法(Multi-Cri‐teria Decision-Making,MCDM)由于结合两者的优点得到广泛的应用[3],MCDM主要分为层次分析法、网络分析方法、模糊逻辑法、逼近理想值排序法等[7],它可以从致灾因子、孕灾环境以及城市本身的承载能力[8]的角度进行综合分析。如Zhong等[9]结合云信息扩散模型与层次分析法,建立山洪灾害风险评估模型;Lin[10]等提出一种基于改进层次分析法和最大似然聚类的山洪综合风险评估法,以广东省为例验证了该方法的可靠性;黄国如等[1]从危险性、易损性角度选取指标建构评估体系,对珠三角地区城镇化前后城市洪涝风险进行分析。
需要指出的是,经验模型评估的准确性取决于洪涝影响因子的选取。然而,在选取影响因子和构建指标体系时,经常依赖于专家知识和专业文献。由于不同学者对灾害的认知和定义不同[8],相关评估方法尚未形成统一的标准,指标评估体系的客观性和一致性均受到限制。降雨作为洪涝灾害最直接的驱动因素,洪灾的发生与一定时段内降雨总量有关,时段内的降雨量对灾害评估起决定性作用,但目前尚未确定哪个指标是评估洪涝灾害的最佳指标。基于此,本文以沿海城市——广东省湛江市赤坎区为例,提出了一个基于k-means聚类和Apriori算法的城市洪涝灾害成因分析框架,采用Apriori算法来分析洪涝灾害的成灾机制,选取降雨、高程、坡度、不透水率和距河距离等因素作为指标[11,12],探索赤坎区洪涝灾害成灾机制。
1 研究区域与数据来源
1.1 研究区域
以广东省湛江市赤坎区为研究区域(图1)。湛江市位于广东省西南部,赤坎区是湛江市的中心城区,区域面积6 205 hm2,地势由西北向东南倾斜,最高海拔43 m,平均海拔19 m,西部、北部为岗丘起伏的台地地区,东南部为低平的海积平原和岛屿。区境内有8条河溪,多年平均降雨量为1 596 mm。赤坎区作为湛江市中心城区,城镇建设用地多,占全区土地总面积的63.16%,加之其地处湛江湾西北岸,属于台风、风暴潮多发地,极易引发洪涝灾害。如2015年10月4日台风“彩虹”从湛江坡头区登陆,赤坎区降雨量达300 mm,多处遭遇洪水侵袭,直接经济损失0.64亿元。

图1 研究区域Fig.1 Maps of the study area
1.2 数据来源
不同持续时间降雨数据来源于广东省水文站、雨量站共440站的长序列雨量资料。DEM数据来源于中国科学院资源环境科学数据中心的遥感影像数据,分辨率为30 m×30 m。土地利用数据来自地理检测云平台土地资源类数据集(分辨率30 m)。历史洪水资料来自广东省洪灾调查数据。1、3、6、12和24 h多年平均最大降雨通过ArcGIS克里金插值得到,不透水率基于土地利用类型重新赋值[13],距河距离的指标使用欧几里得公式计算。
2 研究方法
2.1 k-means聚类
采用k-means聚类方法对各风险指标进行分组,其作用是将大数据划分成有意义的几组(簇),具有“组内差异小,组外差异大”的特点。使用Apriori算法对数据库进行挖掘之前,需将连续指标进行离散。k-means聚类算法是根据观测距离将x划分为k个维度,具体步骤为:
(1)随机抽取k个样本作为初始质心g=1,2,…,k)。
(2)将每个样本点分配到离它们最近的质心,生成k个簇。
(3)对于每个簇,计算所有被分到该簇的样本点xi的平均值作为新的质心,目的是样本点到其所在簇的质心距离最小。对于离散指标,如不透水率,则按原属性分为4类。对于连续指标,如降雨指标、高程、坡度等,使用欧几里得距离作为计算公式将其分成4类:
(4)重复以上步骤,当质心的位置不再发生变化时,迭代停止,聚类完成。
各风险指标按以上流程进行聚类,洪涝灾害等级图根据赤坎区收集的洪涝灾害清单,通过不同淹没深度对市民日常生活的影响[14],将其划为4个等级(表1),其空间分布见图2,各指标分类结果见表2,风险指标空间分布见图3。

表1 赤坎区城市洪涝等级划分Tab.1 Classification of urban flood in Chikan district

表2 洪涝灾害等级与风险指标分类Tab.2 Classification of flood hazards and the risk indicators
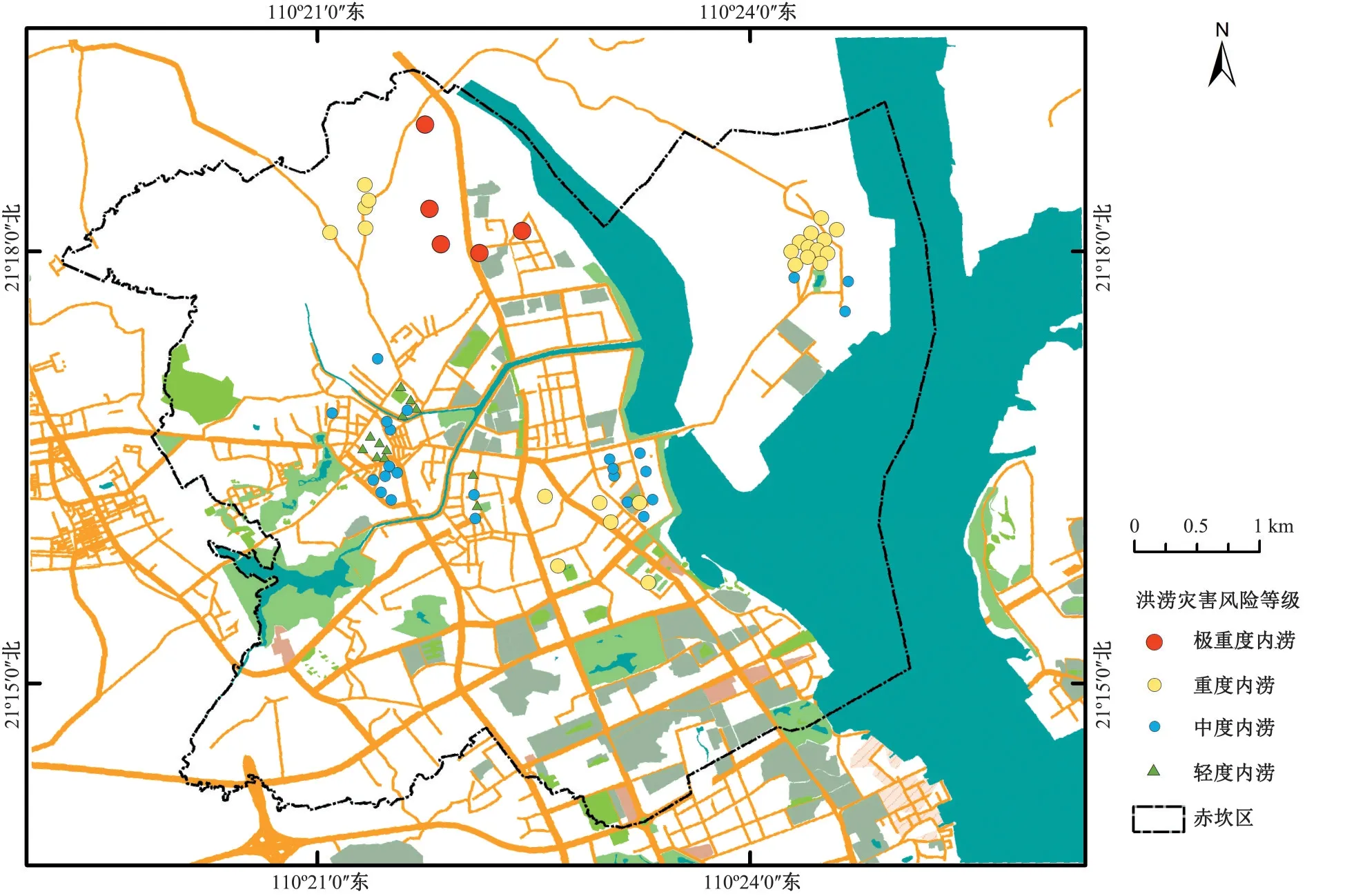
图2 赤坎区洪涝灾害分布图Fig.2 Distribution of urban flood in Chikan district

图3 各风险指标空间分布Fig.3 Spatial distribution of the risk indictors
2.2 Apriori算法
关联规则已在商业、医学和灾害管理等领域得到广泛应用,关联规则挖掘是一种重要的数据挖掘方式[15],如基于多候选项集的Apriori算法,基于模式增长的FP-growth算法和基于垂直格式的Eclat算法。关联规则暗示两个事件之间可能存在的很强关系,是一种非监督学习算法。关联规则表示为:“A→B”,假设I为数据库中所有项的集合,D为数据库中所有事务的集合,其中A∈I,B∈I,且A∩B=∅,即事务集D是I的一个非空子集,并且A、B均包含于D中;其中,A是关联规则的前件,B是关联规则的后件,“A→B”称为强关联规则。“A→B”是否构成强关联规则主要取决于支持度和置信度。
支持度是A和B在数据集I中出现的次数占总数据集的比重P(A∪B),它可以表示为:
置信度是A发生的条件下,B发生的概率,是一种条件概率P(B|A),A对B的置信度为:
Apriori算法采用一种水平搜索的迭代方法来缩小搜索空间,通过设置一组最小支持度(minSup)和最小置信度(min‐Conf),从而生成频繁项集和强关联规则,主要分为两个步骤:
(1)频繁项集的产生。
这一步的目标是发现满足minSup的所有项集,称为频繁项集。
(2)关联规则的产生。
从第一步产生的频繁项集中提取所有满足minConf的规则,称为强关联规则。
2.3 风险挖掘流程
研究所提出的流程(图4)主要分为3个过程:数据收集、数据预处理和关联规则挖掘,其中关键在于关联规则挖掘。首先,整理降雨、高程和洪涝灾害等数据,初步获取各风险指标;将风险指标进行离散化处理并分组;设置一组合适的关联规则阈值(minSup和minConf)进行关联规则挖掘,先识别最佳降雨指标,再提取洪涝成因强关联规则。由于部分灾害等级事件发生较少,原阈值无法获取各等级灾害的强关联规则,需要对小概率事件进行抽样,重新设置关联规则阈值,对其进行深层次的分析,获得研究区域洪涝成灾机制。
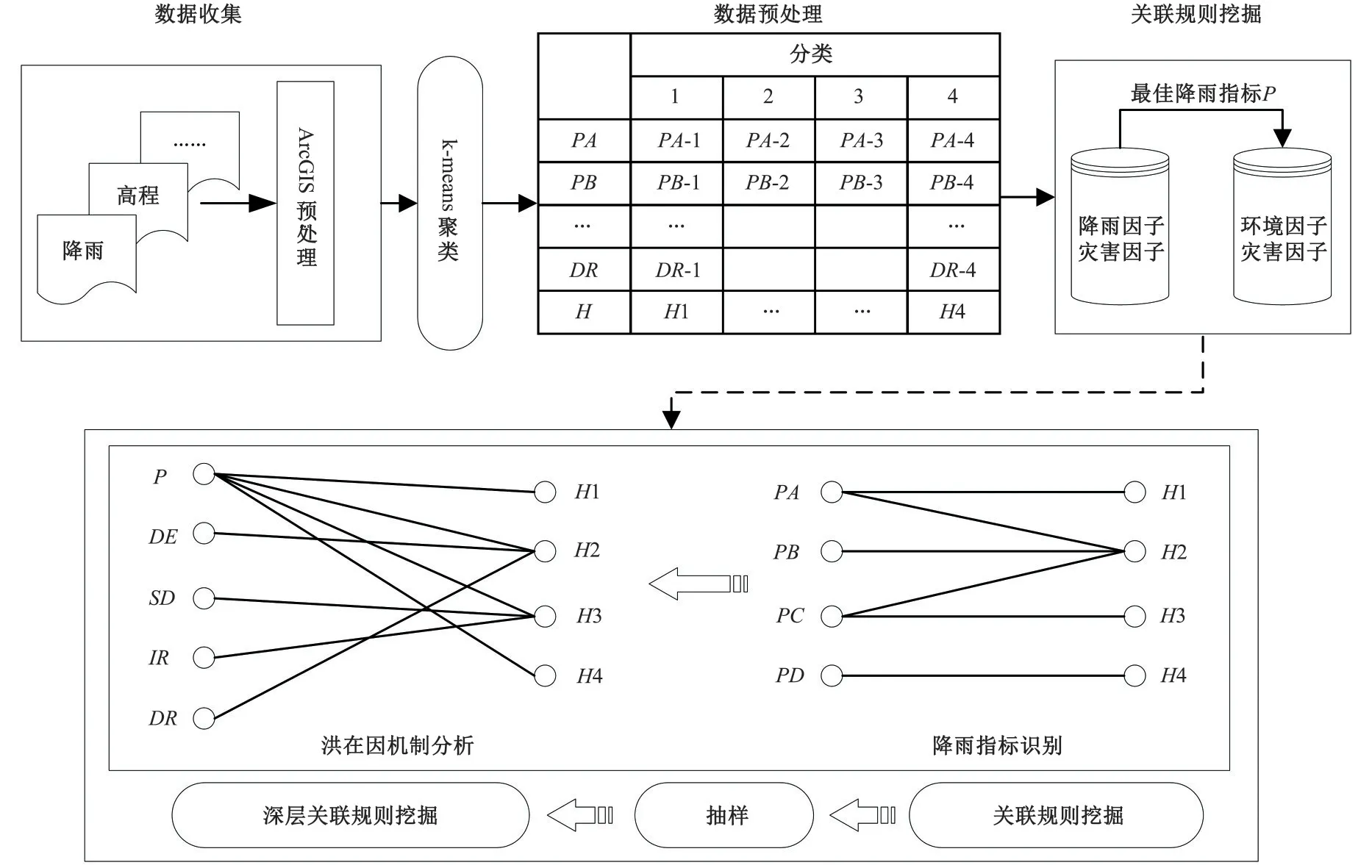
图4 基于Apriori算法和k-means聚类的分析框架Fig.4 Framework based on Apriori algorithm and k-means clustering
3 结果与讨论
3.1 降雨指标的识别
根据表1各指标构建数据库(database 1),初设关联规则阈值进行规则提取,多次试验并调整阈值[16,17],直至提取到满意的结果,剔除明显不存在因果关系的关联规则。当minSup=0.19,minConf=0.42时,可挖掘到较为满意的结果,如表3所示。

表3 多降雨指标的关联规则 %Tab.3 Association rules for multiple rainfall indices
其中,规则1支持度为33.29%,置信度为55.35%,表明包含PD-2(多年平均最大24 h降雨为167.50~167.87 mm)和H2(中度内涝)的洪涝事件占33.29%,在PD-2的前提下,发生H2的概率为55.35%;对于规则2~11,关于H2的强关联规则中,在支持度相近的情况下,包含PD的关联规则置信度大于55.35%,均高于不含PD的规则,H2的出现通常伴随着PD,这表明H2的发生与PD有着紧密的联系。关于H3(重度内涝)的关联规则12~14前件也均包含PD项集,表明大多数洪涝灾害与PD有较高的关联性。
由于中度内涝和重度内涝的发生率较高,初次挖掘只提取到关于H2或H3的关联规则,对数据库进行抽样,提取H1(轻度内涝)、H4(极重度内涝)事件,构建新的数据库(database 2),minSup=0.37,minConf=0.80,生成16条强关联规则,见表4。

表4 深层挖掘多降雨指标的关联规则 %Tab.4 Association rules based on multiple rainfall indices after sampling
由表4可见,这些规则的前件均包含PD,且置信度均达98%;规则9~16意味着H4的出现,必然伴随着PD的发生。然而值得注意的是,规则前件的降雨指标中,灾害更严重的“H4”相比“H1”,降雨量级反而更小,降雨对于灾害的发生固然重要,但推动H4的发生可能还存在其他关键因素。这一结论与前人的研究成果相符[18],洪涝与一定时间内降雨总量有关,几小时的短历时强降雨,由于总量较小,一般难以形成大洪水;此外,降雨阈值对于洪水产生至关重要[19],不同区域成灾的降雨历时不同。结合表3分析,与其他降雨指标相比,PD是分析赤坎区洪涝灾害成灾机制最适合的降雨指标。
3.2 洪涝成灾机制分析
不同研究区域的地形地貌、水文气象和社会经济条件不同,造成洪涝灾害发生的机制也不同,单风险因素对一个地区的洪涝发生影响可能较小,与其他因素耦合则可能产生重要影响。将上一节最适降雨指标PD与环境因素、历史洪涝灾害数据结合构成新的数据库(database 3),按照同样的方法调试出关联规则阈值,minSup=0.10,minConf=0.50,如表5所示生成风险指标的频繁项集。

表5 风险指标的频繁项集 %Tab.5 Frequent item sets for risk indicators
如表5所示,赤坎区洪涝灾害的等级主要为中度和重度,结合图3可知,赤坎地势较为平缓,整体起伏不大,城镇居民用地居多,径流系数大导致坡面汇流增加,坡度大小又影响汇流时间,坡度缓容易积水,在台风、风暴潮等极端事件的驱使下,洪涝灾害发生的机率将大幅提高。以IR(不透水率)为例,(IR-4,H2)和(IR-4,H3)均为频繁项集,支持度分别为32.60%和24.13%,表明洪涝灾害常发生在不透水率高的地方。
当minSup=0.10,minConf=0.50,database 3挖掘到关于H2的17条关联规则;为获取其他等级灾害的关联规则,对其抽样构成数据库database 4,新阈值当minSup=0.12,minConf=0.55,提取到关于H3的30条强关联规则,多指标的关联规则风险分布见图5。图5(a)规则前件大部分包含PD-2,其中{PD-2}→{H2}支持度最高,sup=33.29%,conf=55.35%,表明PD-2作为前因与H2一同出现的可能性是最高的,再次证明PD是洪涝事件发生的最直接驱动要素;{PD-2,DR-1}→{H2}置信度最高,conf=76.34%,说明环境因素中,DR-1致中度内涝灾害的作用最大。如图6所示,设minSup=0.10,minConf=0.37,获取的14条关于H2关联规则,支持度相差不大的情况下,前件包含PD-2的规则置信度均有不同程度的提升,提升幅度为7.65%~25.74%,其中DR-1的提升幅度最大,印证PD是中度洪涝事件发生的最直接驱动要素,环境因素中DR-1的致灾效果最显著。

图5 多指标关联规则分布Fig.5 Distribution of multi-factor association rules
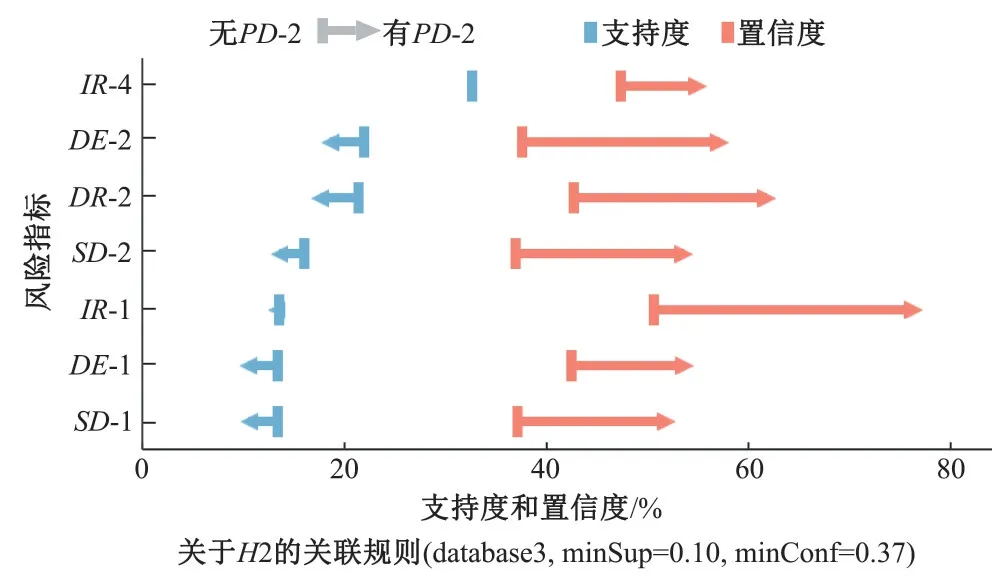
图6 降雨对单指标关联规则的影响Fig.6 Effects of rainfall on association rules for single factors
图5(b)相较于(a),PD-2作为H2的最直接驱动要素,在关于H3的规则中,其地位有所下降,PD-1和PD-2作为规则前件,出现的频数分别为6次和8次,意味着重度内涝发生机制更为复杂;规则{PD-2,DE-1}→{H3}和{PD-2,SD-1}→{H3}置信度较高,分别为86.8%和80.71%,重度内涝发生机制中,DE-1(高程-7~8 m)和SD-1(坡度≤1.72°)更为敏感;由图5(b)可知,前件无PD的规则{SD-1}→{H3}和{SD-2}→{H3}支持度相近,随着坡度的平缓,置信度提高12%,且前件包含SD-1的规则置信度均超过70%。
总的来说,赤坎区城镇居民地区多,离河距离≤284.61 m是中度内涝高发地,坡度≤1.72°或高程-7~8 m的区域是重度灾害的易发地。究其原因,PD是造成当地洪水的直接原因,对于沿海区域,持续时间长的强降雨和风暴潮的都是诱发洪水的重要因素[20],离河较近的地方自然更易受到两者耦合作用,直接导致沿海洪水。加上赤坎区内部地势低洼平缓,容易积水,外部潮位影响排水系统[21],海水倒灌,在多因素耦合情况下,易引发严重的洪涝灾害。
4 结 论
以沿海地区——广东省湛江市赤坎区为例,构建了基于kmeans聚类和Apriori算法的城市洪涝灾害成因分析框架,提取强关联规则,探索风险因素与洪涝灾害的因果关系。主要结论如下:
(1)多年平均最大24 降雨(PD)是分析赤坎区洪涝灾害成因最合适的降雨指标。降雨作为洪涝灾害最直接的驱动因素,关联规则挖掘发现,与其他降雨强度指标相比,各等级灾害均与PD指标有紧密联系。
(2)灾害多发生于不透水率高的居民区,沿海区域由于风暴潮原因,更易发生沿海洪水,潮位影响海水倒灌,地势平缓低洼地区容易引发更严重的洪涝灾害。
(3)PD-2作为中度洪涝事件发生的最直接驱动要素,在重度内涝成灾机制中其地位有所下降,环境因素的重要性可能提升。由于受到资料的限制,数据库未考虑排水管网密度、潮汐等重要因子,后续的研究可以此进行深入分析,Apriori算法挖掘出的结论可为城市洪涝成因分析提供参考。

