ARMA模型在预测全球平均温度情况中的应用

程 研，华志强，黄玉洁，侯云艳

（内蒙古民族大学 数理学院，内蒙古 通辽 028043）

0 引言

工业化以来，人们对自然界能源的大肆开发导致恶劣的全球变暖问题的发生，若要缓解全球变暖的危害，当务之急是对未来气温变化情况有所掌握，所以，研究气温预测的相关问题具有重要的现实意义。

进入气象大数据的时代，诸多学者在气温预测上取得了丰富的理论成果。雷凯[1］基于LSTM 深度学习模型对未来合肥市日最高气温进行预测，表明LSTM 的预测精度高，模型是有效的。王芳等[2］针对重庆市温度资料，结合小波神经网络(WNN)对温度进行估计，结果显示模型的相对误差较小。姜文瑞等[3］借助某地30 年的气象数据，采用决策树的分类与回归树分类方法，为气象预测研究提供了参考。朱晶晶等[4］基于平均气温数据，建立气温的SVM 回归预报模型，实验显示SVM 算法在气温短期预测中有明显的适用性。付正辉等[5］建立灰色马尔科夫动态预测模型，完成模型准确性的检验，对某地当今至2050 年的平均气温进行预测。

基于上述研究，近些年时间序列分析方法也受到广大学者的关注，时间序列分析方法在自然环境[6-7］、医疗防疫[8-9］、经济发展[10-11］等方面有出色的表现，例如，相旭东等[6］利用Marion 站点的地表月平均温度资料来预测未来两年的地表月平均温度，证明ARIMA(p,d,q)模型适用于预测地表月平均温度；程颖等[8］基于某医院的非伤寒沙门菌发病率数据预测发病率，对病情控制有指导作用；瞿海情等[11］利用ARIMA(p,d,q)模型，对湖北省GDP 未来趋势进行预测，为地区治理奠定理论基础。

综上所述，基于气温预测的重要性，采用时间序列分析方法，对全球平均气温序列进行数据预处理，模型分析和模型预测等建立ARMA(p,q)模型，对全球气温变化情况进行预测，为制定应对方案提供科学参考。

1 模型建立与统计分析

1.1 记号与假设

为研究方便，引入记号并做出相应假设，xt表示第t年的全球平均气温，εt表示第t年时人类活动和自然因素对平均温度产生的影响或者干扰，而且有以下假设：

（1）εt是零均值白噪声，即εt~WN( 0,σ2)。

（2）xt是二阶矩平稳的，xt期望和方差是存在的，记Ext=μ,Varxt=σ2，协方差cov(xt,xs)=γt-s。

引理设随机序列{} 满足：

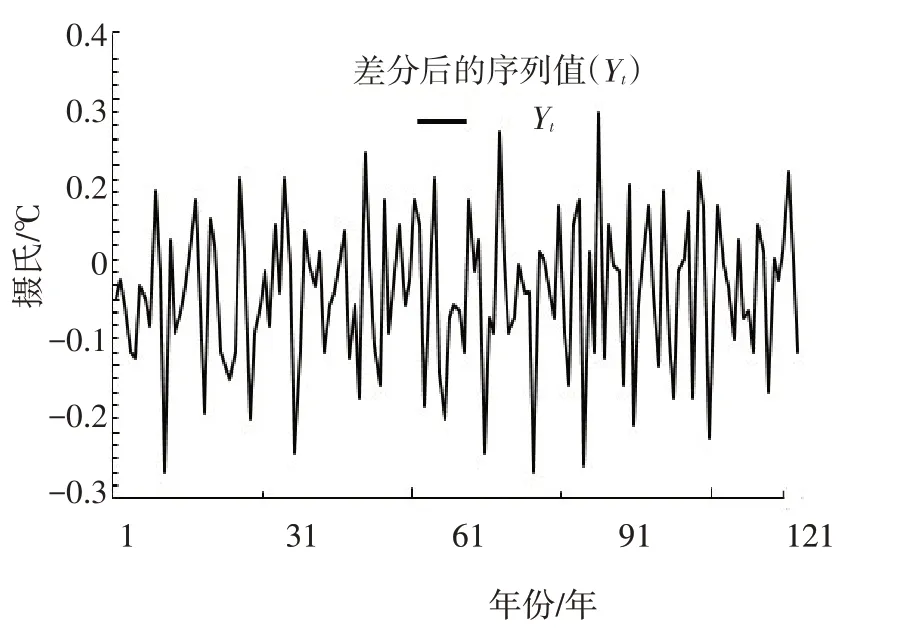
（1）xt=ϕ0+ϕ1xt-1+…+ϕpxt-p+εt-θ1εt-1-…-θqεt-q；（2）ϕp≠0,θq≠0 且E(xtεt)=0,∀s

1.2 参数估计

若x1,x2,…,xn是序列{xt} 的n个观测值，有如下命题：

命题1xt为可逆的ARMA(p,q)模型，即

则ξ的矩估计量为，对于模型（1），记yt=xt-，则{yt} 仍为可逆的ARMA(p,q)序列。

证明由（1）以及{yt} 可知，{yt} 是原可逆的ARMA(p,q)模型{xt} 中心化得到的，-ξ=0，此时{yt}依然满足引理条件，故{yt} 为中心化的可逆的ARMA(p,q)模型。

命题2若满足下列条件：

（1）εt∼WN(0,σ2ε)；（2）Θq(B)=1-θ1B-…-θqBq；（3）Φp(B)=1-ϕ1B-…-ϕpBp。则命题中的参数ϕ,θ的最小二乘估计为

证明首先对序列建立AR模型，取AR模型阶数的上界得到AR模型的阶数估计和模型残差可得相近的ARMA(p,q)模型，这里引入是待定参数。最后对函数进行极小化，得到参数的最小二乘估计所以，函数f(ϕ,θ)写成那么，最小二乘估计由方程决定，在满秩的情况下可解出最小二乘估计，即式（2）。

命题3若序列{}的观测值期数为n，指定的时滞期数为m，延迟k期的自相关系数估计值为，则

即QLB统计量近似服从自由度为m的卡方分布。

证明已知因为独立同分布且近似服从正态分布，对进行标准正态变换得到有m个相互独立的χ2(1)变量之和服从χ2(m)分布，根据正态分布和卡方分布之间关系，可得由此可得式（3）。

1.3 预测

定理对于平稳可逆的ARMA() 模型，当在上述式中Gi+l=Wi时，则第l步的预测误差的方差满足线性预测方差最小原则，即

证明时间序列模型可表示成传递函数的形式，由平稳模型的特点以及线性函数的可加性知，

当Gi+l=Wi时，预测方差最小。此时，xt+l的预测值是预测误差为

2 数值模拟

2.1 数据平稳化处理

图1 为连续140 年的全球平均温度值，从图1 中知，前138 年的平均温度值是非平稳时间序列且序列可由直线趋势模型拟合。直线趋势模型的特点是一阶差分为常数，令Yt=xt-xt-1可实现趋势的消除。差分后的序列值始终在常数值附近波动且波动的范围有界，见图2。

图2 一阶差分的序列Fig.2 Sequence of the first order difference

现采用ADF 单位根检验法判断差分后的序列是否为平稳时间序列，ADF 检验t统计量对应的值是-10.162 21，-10.162 21小于1%、5%、10%检验水平的临界值，则差分后的序列是平稳的，见图3。

图3 单位根检验Fig.3 Unit root test

2.2 白噪声检验

白噪声序列要满足γ() =0,∀k≠0，所以原假设和备择假设可为：

在命题3 条件下，当统计量的P值小于α（α=0.05）时，就以1-α的置信水平拒绝原假设，则该序列是非白噪声序列，反之，该序列为白噪声序列。在短期延迟内，Q统计量值对应的P值小于0.05，则该序列是非白噪声序列，见图4。

图4 自相关和偏自相关图Fig.4 Autocorrelation and partial autocorrelation graph

2.3 模型分析

2.3.1 模型定阶 由ACF 和PACF 表现出来的性质，选择合适的阶。根据图4 可知，ACF 和PACF 在延迟1 期时，有明显的超出2 倍标准差且多期后的ACF 和PACF 不趋于0，说明两者是拖尾的，则拟合为ARMA(1 ,1) 模型。

2.3.2 参数估计 为简化计算，在命题2 下的ARMA（p，q）模型，假设过去未观测到的序列值为0。见图5，ϕ1=0.467 827,ϕ0=0.008 066,θ1=-0.831 704，故模型为

图5 参数估计Fig.5 Estimated parameters

2.3.3 模型检验 模型提取的信息越充分说明模型越有效，因此，模型的显著性检验为残差序列的纯随机性检验，残差序列的ACF 和PACF 都在2倍标准差之内且Q统计量对应的P值大于0.05，故模型通过显著性检验，见图6。

图6 残差检验图Fig.6 Residual test graph

参数的显著性检验是检验每一个未知参数是否显著为零，所以假设检验：

在正态分布假设下，为第j个未知参数的最小二乘的估计值且是不可观测的，用最小残差平方和得到可构造检验未知参数显著性的t检验统计量：或α大于检验统计量的P值时，则拒绝原假设，认为该参数是显著的。由图5 可知，估计值对应的统计量的P值小于0.05，故系数通过显著性检验。

2.3.4 预测数据 预测是指借助拟合模型，利用序列中观测值来估计未来某时刻的序列值。对于平稳可逆的ARMA(1 ,1) 模型（6），已知，预测未来数据所示，可近似得到，见图7。

图7 模型预测值Fig.7 The value of model prediction

2.3 误差分析

模型对未来趋势的表现可以判断模型的优劣，保留一部分数据作为测试集，利用之前的数据进行外推，计算实际值与预测值的误差。误差分析指标为平均绝对百分误差(MAPE)，若MAPE 小，则模型的拟合程度高。

由上得知，在误差允许范围内，模型对历史数据的拟合程度较高，建模效果较好。

3 结论

气温变化是气候研究的重点问题，ARMA 模型能快速地从样本序列中分析气温变化的情况，但在建模时要考虑相关因素对预测结果的干扰，为保证后续预测结果的准确度，要用新观察的数据来修正模型。因此，运用时间序列分析方法，结合EViews 工具对气温预测展开研究，可为预防灾害和自然资源利用提供理论依据。