工业纯钛TA2 压载荷下含表面裂纹板应力强度因子

张雨宸，姚锡铭，裴 琦，周昌玉，贺小华

（南京工业大学机械与动力工程学院,江苏 南京 211816）

0 引言

工业纯钛具有综合力学性能优异，耐腐蚀性能好且具有较好的可加工性能等特点，成为国内常用于钛制设备和容器的主要材料之一，广泛应用于石油化工、生物制药、航天航空等领域[1−2]。随着钛材的大量使用，含缺陷的钛制承压结构的安全性也显得愈发重要[3]。裂纹是最危险的缺陷形式，轻则导致泄露事故的发生，重则引起严重的脆性断裂爆破事故。应力强度因子广泛应用于裂纹体强度与疲劳裂纹扩展研究，是评价含裂纹结构强度的重要参数。因此，有必要了解和掌握工业纯钛裂纹体应力强度因子影响因素，合理评价裂纹体的结构完整性[4]。

早期研究中，文献[5–8]通过理论分析研究了拉弯载荷下Ⅰ型表面裂纹的应力强度因子，并提出了近似表达式，其中Raju，Newman 提出的表面裂纹近似解具有良好的适用性，至今仍被作为基本模型运用于各类表面裂纹断裂参量的相关研究。有限元方法具有良好的经济性、可行性和精确性，在工程和科学计算领域应用广泛，文献[9–11]基于有限元方法研究了拉伸或弯曲载荷下复合型表面裂纹应力强度因子分布规律。结果表明，受拉载情况下，裂纹不同几何参量（裂纹倾角β，裂纹相对深度a/t，裂纹形状系数a/c等）对表面裂纹应力强度因子KⅠ，KⅡ，KⅢ变化规律产生影响。文献[12–14]基于有限元计算结果，提出拉伸或弯曲条件下复合型表面裂纹应力强度因子经验公式，此时表面裂纹同时存在应力强度因子KⅠ，KⅡ，KⅢ。外压或压载荷是压力容器和管道常见载荷之一，压载荷下有关应力强度因子的研究大多关注穿透裂纹形式。文献[15–17]通过解析法和有限元方法研究了压载荷下复合型穿透裂纹应力强度因子分布规律。此时，I 型应力强度因子KI=0，仅存在II 型应力强度因子KⅡ。

笔者针对工业纯钛TA2 含半椭圆表面裂纹板模型，采用Abaqus 有限元数值分析方法，研究压载荷下复合型表面裂纹应力强度因子KⅡ和KⅢ分布规律，并提出了适于工程应用的单轴压载下含半椭圆表面裂纹板的应力强度因子KⅡ和KⅢ解。

1 基本理论

在经典断裂力学中，将裂纹按受载后裂纹面相对位移方向将裂纹分为张开型裂纹（Ⅰ型）、滑移型裂纹（Ⅱ型）、撕开型裂纹（Ⅲ型）[18]。

Ⅰ、Ⅱ、Ⅲ型裂纹前缘应力场分布如图1 所示，其表达式通过Westergaard 复变函数方法推导出[11]。实际裂纹结构并不会呈单一受载形式，裂纹前缘的应力应变场应由3 种不同类型裂纹的独立表达式组合叠加而成。在拉伸作用下，裂纹表面不存在相互作用力，因此裂纹表面相对自由。对于受单轴压载荷作用下的闭合裂纹，由于物质的不可侵入特性，上下裂纹面并不会发生相互穿透，所以裂纹前缘Ⅰ型分量不存在即为0，这点在文献[17,19]中都有提到，并且有具体推导过程。实际压载荷下裂纹前缘应力应变场分布公式如式（1）：

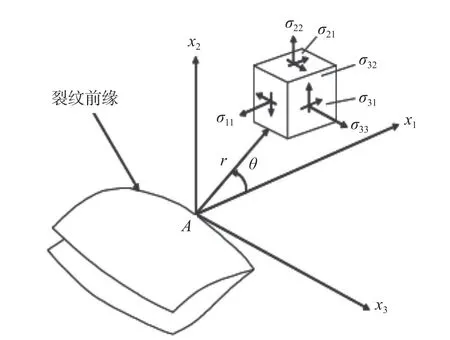
图1 裂纹前缘应力分布Fig.1 The scheme of stress at crack front

2 有限元模型分析

针对工业纯钛TA2 含半椭圆形表面裂纹板模型，笔者选用有限元软件Abaqus 对其进行三维数值模拟。板结构几何模型如图2 所示。平板宽度与长度分别用2W和2H表示，且均为200 mm，试样厚度为t，裂纹长度为2c，裂纹深度为a，裂纹倾角为β，表征裂纹面与加载方向之间的角度，裂纹前缘椭圆偏心角为θ，A为裂纹前缘最深处点，B为裂纹前缘与板自由面交点。在单轴压载荷作用下，裂纹板下端面施加位移全约束，上端面施加均匀载荷σy=100 MPa。

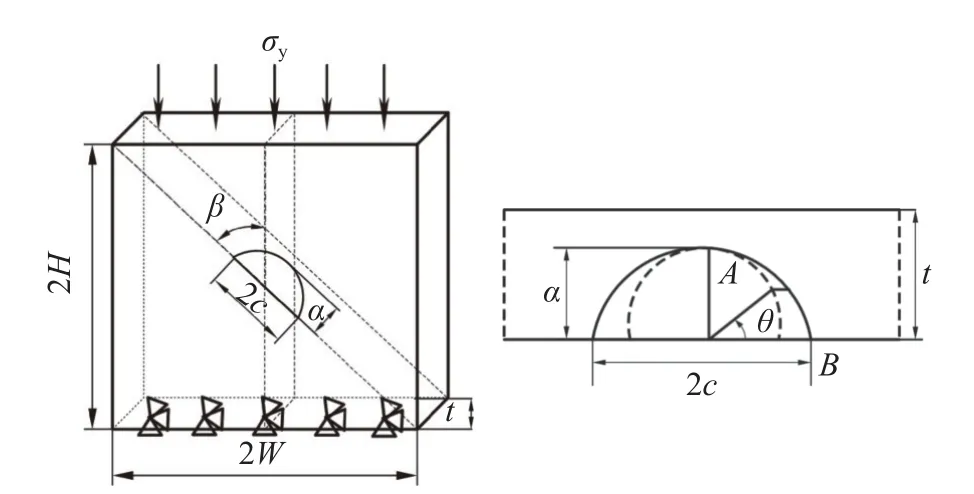
图2 含半椭圆表面裂纹板几何模型Fig.2 Geometric model of semi-elliptical surface crack in plate

材料选用TA2 工业纯钛，弹性模量E=113.1 GPa，泊松比ν=0.348。有限元计算模型参照文献[20]提出的建模方式。由于复合型裂纹存在几何不对称效应，需对裂纹体建立全模型计算。应力强度因子通过Abaqus 中“围道积分”方法获得。承受压载荷的裂纹板，裂纹面产生接触。使用罚函数表征裂纹表面之间的切向摩擦力，同时将法向接触设置为接触后允许分离的“硬接触”，防止可能发生的穿透现象。裂纹整体模型由含裂纹前缘的part1 和剩余平板part2 组成，part1 中裂纹前缘用楔形单元和蜘蛛网结构细分，网格类型为C3D8R，选用中心节点为0.25 的二阶四元单元模拟裂纹尖端奇异性。part1 除去裂纹前缘剩余部分选取C3D10自由网格进行划分；part2 部分选用结构网格行进划分。part1 与part2 采用绑定约束，最大化消除两种网格类型连接产生的误差。通过转动part1 达到变换裂纹倾角β的效果，大大简化建模时间成本，并且保证相同模型网格精确性，有限元计算模型如图3所示。表1、2 提供了网格敏感性分析。不同网格尺寸下KⅡ，KⅢ最大相对误差为3.82%，满足网格敏感性要求。选取最小网格尺寸0.1 mm，裂纹前缘周向网格数120。

表1 最小网格尺寸网格敏感性分析（a/c=0.2，a/t=0.4，β=45°，θ=30°）Table 1 Verification of meshing on minimum sizes of element（a/c=0.2，a/t=0.4，β=45°，θ=30°）

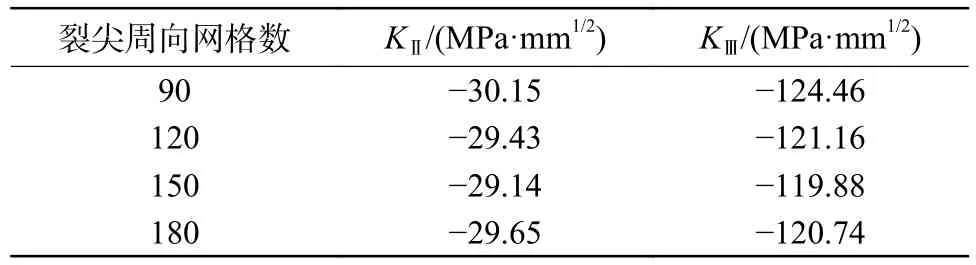
表2 裂纹前缘裂尖周向网格敏感性分析（a/c=0.2，a/t=0.4，β=45°，θ=30°）Table 2 Verification of meshing on numbers of element along crack front（ a/c=0.2， a/t=0.4， β=45°，θ=30°）

图3 含半椭圆表面裂纹板有限元模型Fig.3 Finite element model of semi-elliptical surface crack in plate

提取a/t=0.4 时，a/c=0.2，0.4，0.6，0.8，1 时分别对应的裂纹表面点B和裂纹深处点A的KⅠ有限元解与Newman-Raju[6]和GB/T 19624-2019[21]解对比，验证模型准确性。如图4 所示，有限元计算结果可以满足精度要求。

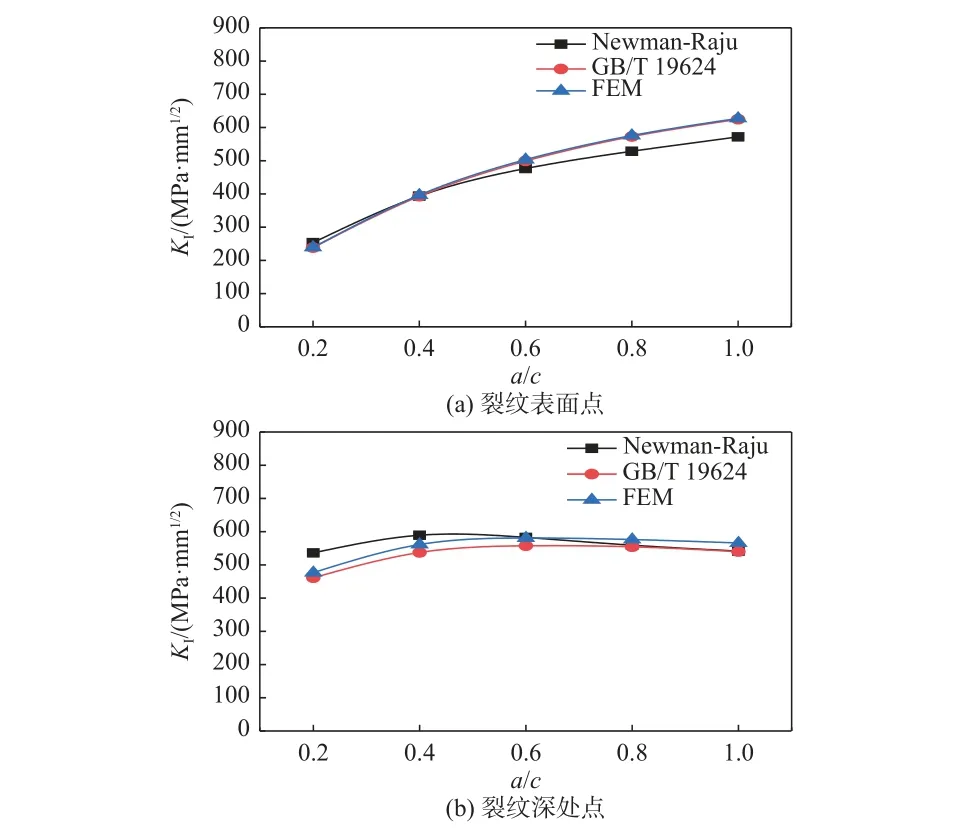
图4 有限元结果与Newman-Raju 和GB/T 19624 应力强度因子解对比Fig.4 Comparison of stress intensity factor by finite element results,Newman-Raju and GB/T 19624 solutions

3 压载下表面裂纹应力强度因子影响因素分析

本节主要考虑裂纹倾角β(0°，15°，30°，45°，60°，75°，90°)，裂纹相对深度a/t(0.2，0.4，0.6，0.8)，裂纹形状系数a/c(0.2，0.4，0.6，1)，摩擦系数μ(0，0.3，0.5，0.7)与侧压系数λ(0，0.25，0.5，1)对压载荷下应力强度因子的影响。为了更为直观地观察半椭圆形表面裂纹应力强度因子的分布规律，使用Newman 和Raju 于1981 年提出的Kr和Q参数对其进行归一化处理[6]，应力强度因子分量Ki、归一化参数Kr、Q可分别表征为：式中分别表征归一化应力强度因子Ⅰ，Ⅱ，Ⅲ型分量。

3.1 裂纹倾角对应力强度因子影响

图5、6 分别给出了a/c=0.4，a/t=0.8，μ=0.3 时，分别对应不同裂纹倾角β=15°，30°，45°，60°，75°时压载荷下表面裂纹表面和裂纹前缘的应力云图。图7 给出了a/c=0.4，a/t=0.8，μ=0.3 时，分别对应不同裂纹倾角β=0°，15°，30°，45°，60°，75°，90°时压载荷下表面裂纹应力强度因子Ⅱ型和Ⅲ型分量。

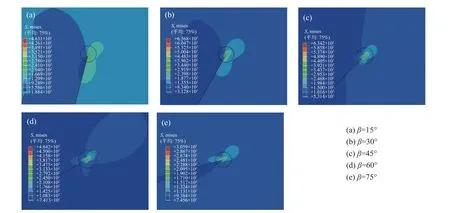
图5 裂纹表面Mises 应力云图Fig.5 Mises stress of crack surface

图6 裂纹前缘Mises 应力云图Fig.6 Mises stress along crack front

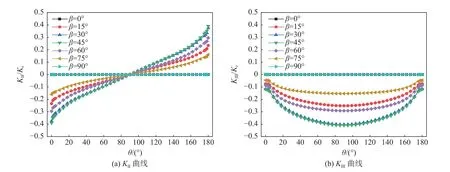
图7 应力强度因子KⅡ，KⅢ随β 变化曲线Fig.7 Variation of stress intensity factors KⅡ, KⅢ along crack front with β

由图5 可以看出，复合型裂纹表面点B处裂纹尖端Mises 应力场沿裂纹面分布不对称。随着裂纹倾角的增大，Mises 应力先增大再减小，在β=30°时出现最大值，裂纹尖端应力分布区域沿逆时针旋转。图6 中，整个裂纹前缘处Mises 应力在β=45°时出现最大值，其次是在β=30°，60°下，Mises 应力最低出现在β=15°，75°下。对比图5、6，不难发现β=30°，45°时，Mises 应力最大值在裂纹深处点A；当β=15°，60°，75°时，Mises 应力最大值在裂纹表面点B，这表明裂纹倾角的改变影响表面裂纹前缘应力分布。

由图7(a)可以看出，应力强度因子KⅡ关于θ=90°呈反对称分布。裂纹倾角β=45°时，KⅡ变化范围最大，其次是β=30°时，并且曲线较为接近，随后是β=60°、15°和75°的KⅡ，KⅡ分布规律与β=30°时相似。这与图6 应力云图中应力最大值随裂纹倾角的变化规律吻合。β=0°和90°时，KⅡ随裂纹前缘椭圆偏心角分布近似为直线，并且接近于0。表面裂纹KⅡ最大值位于表面裂纹两侧接近自由平面区域，在裂纹最深处(θ=90°)最小。由图7(b)应力强度因子KⅢ关于θ=90°呈现对称分布，且随裂纹倾角变化规律与KⅡ类似。表面裂纹KⅢ最大值（绝对值）位于表面裂纹最深处，在裂纹接近自由平面时最小。

3.2 裂纹相对深度对应力强度因子影响

图8 给出了a/c=0.2，β=45°，μ=0.3 时，裂纹相对深度a/t=0.2，0.4，0.6，0.8 对应的压载荷下表面裂纹应力强度因子Ⅱ型和Ⅲ型分量。

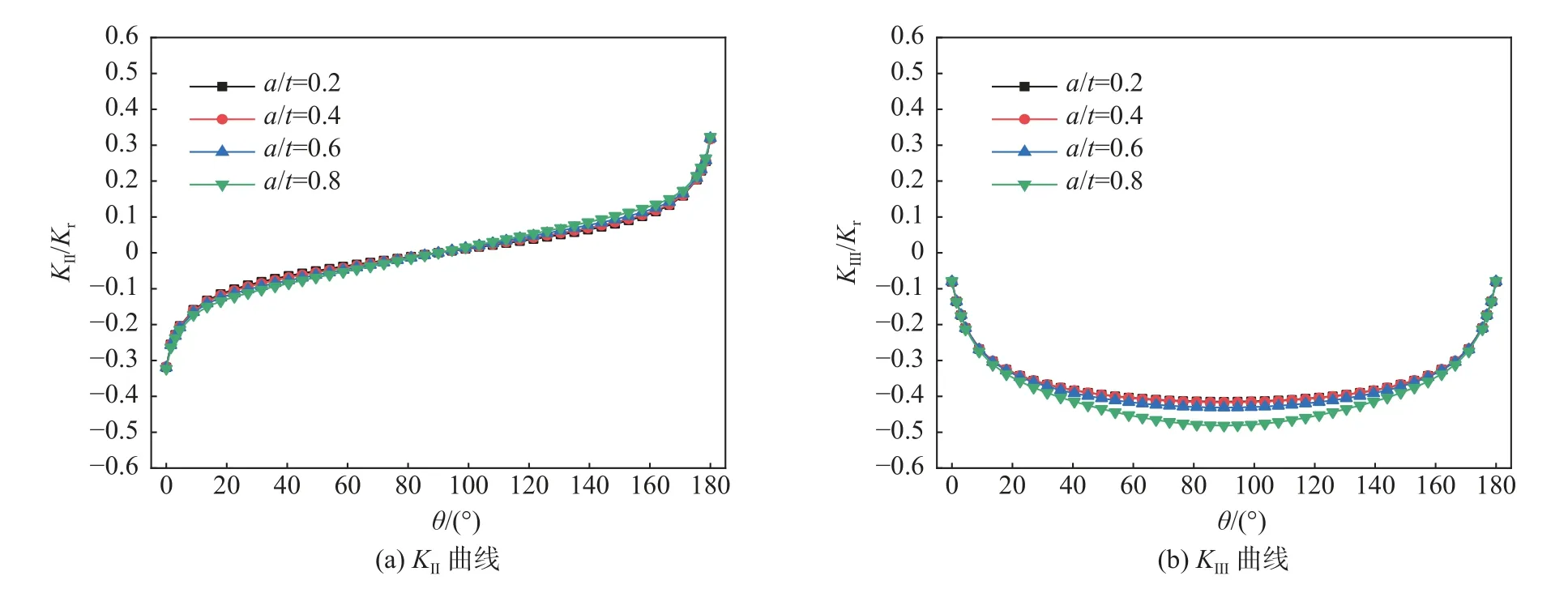
图8 应力强度因子KⅡ，KⅢ随a/t 变化曲线(β=45°)Fig.8 Variation of stress intensity factors KⅡ, KⅢ along crack front with a/t (β=45°)

从图8 可以看出，在固定裂纹形状a/c，裂纹倾角β时，应力强度因子KⅡ和KⅢ绝对值随着裂纹相对深度a/t的增加呈现增大趋势，但是变化幅度较小。这表明在单轴压载荷作用下，裂纹相对深度对裂纹前缘处KⅡ和KⅢ分布影响程度较弱。

3.3 裂纹形状系数对应力强度因子影响

图9 给出了a/t=0.8，β=45°，μ=0.3 时，裂纹形状系数a/c=0.2，0.4，0.6，1 对应的压载荷下表面裂纹应力强度因子Ⅱ型和Ⅲ型分量。

图9 应力强度因子KⅡ，KⅢ随a/c 变化曲线(β=45°)Fig.9 Variation of stress intensity factors KⅡ, KⅢ along crack front with a/c (β=45°)

从图9(a)可以看出，在固定裂纹相对厚度a/t，裂纹倾角β时，应力强度因子KⅡ随裂纹形状系数的增大而变大，并且以θ=90°为分界线，大于90°时，其曲线形状逐渐由内凹变为外凸。图9(b)中，应力强度因子KⅢ随裂纹形状系数的变化与KⅡ截然相反，随着裂纹形状系数的增大，其绝对值变小。这表明KⅡ，KⅢ对于裂纹形状系数影响变化较为敏感，随着形状系数的增大由KⅢ主导逐渐变为KⅡ主导。KⅢ在θ=0°和180°附近时没有趋向于0，产生有波动，这是由于接近裂纹面位置处存在奇异性。文献[12,22]指出裂纹表面处奇异性与自由表面效应和泊松比有关。

3.4 摩擦系数对应力强度因子影响

图10 给出了a/c=0.4，a/t=0.8，β=45°时，分别对应摩擦系数μ=0，0.3，0.5，0.7 时压载荷下表面裂纹应力强度因子Ⅱ型和Ⅲ型分量。

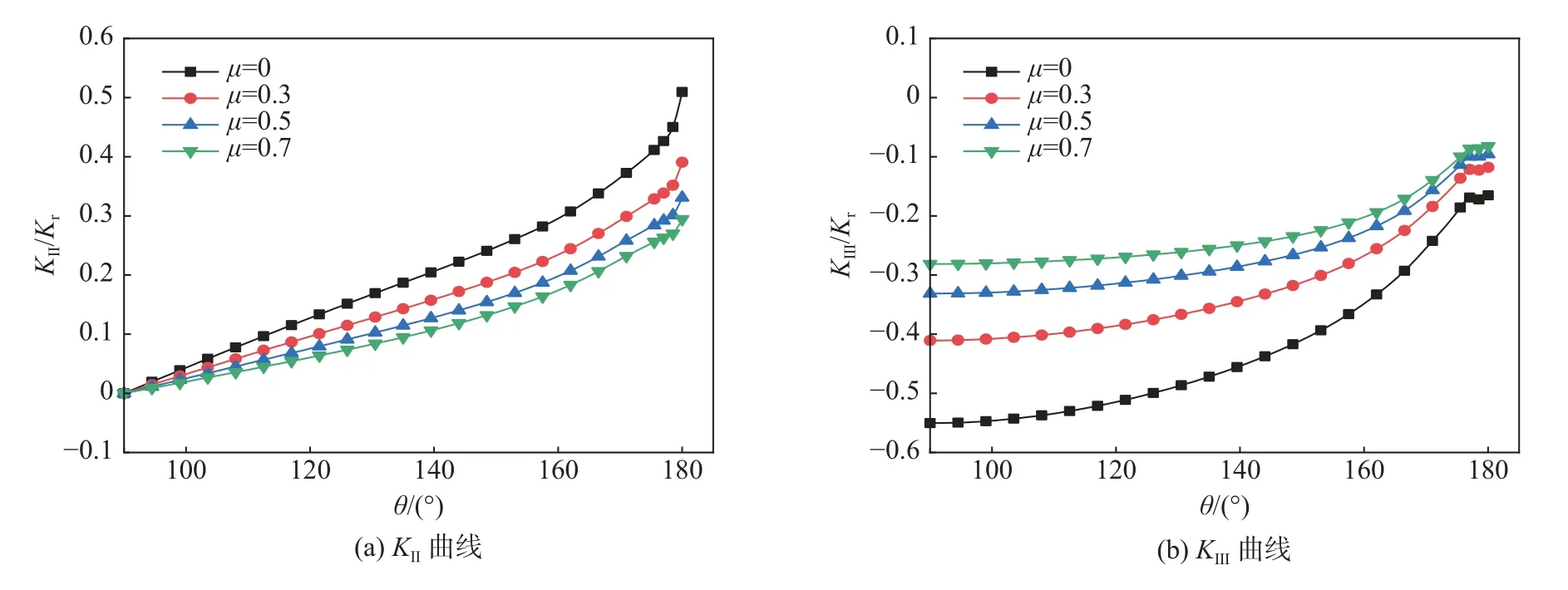
图10 应力强度因子KⅡ，KⅢ随μ 变化曲线(β=45°)Fig.10 Variation of stress intensity factors KⅡ, KⅢ along crack front with μ (β=45°)

图11 给出了a/c=0.4，a/t=0.8，摩擦系数μ=0，0.3 时，分别对应裂纹倾角β=30°，45°，60°时压载荷下表面裂纹前缘的应力强度因子Ⅱ型和Ⅲ型分量。

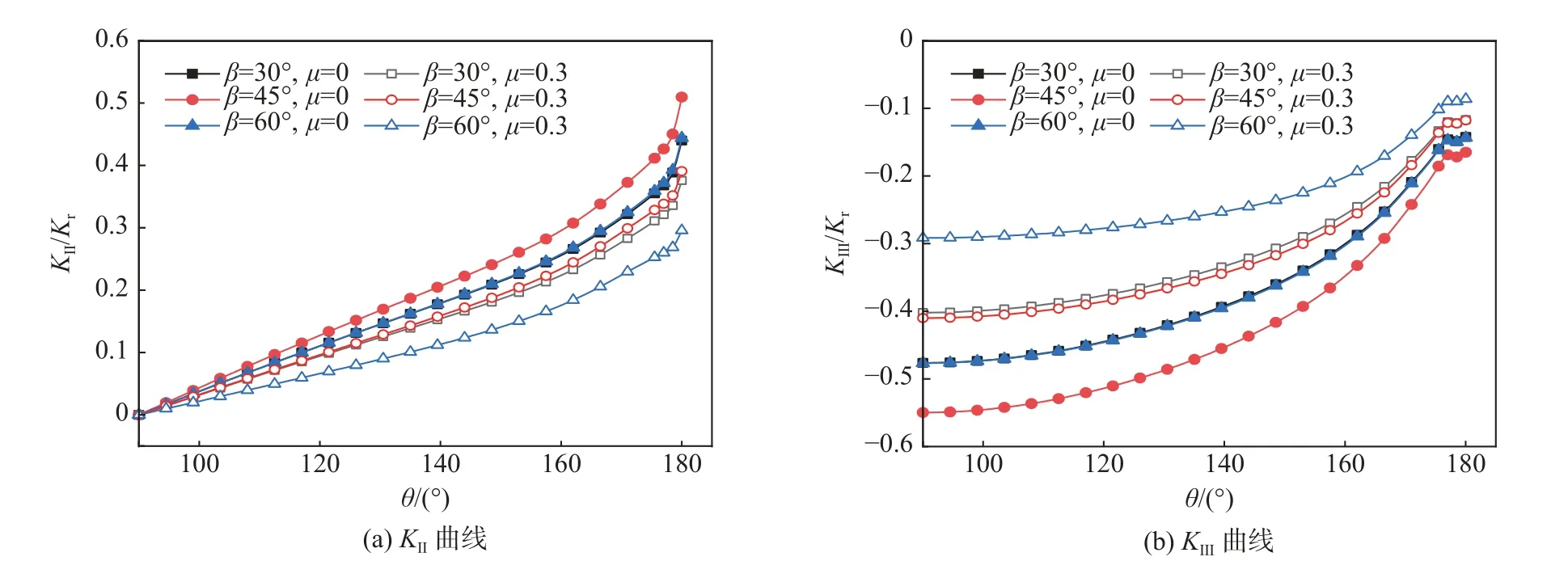
图11 应力强度因子KⅡ，KⅢ随β 变化曲线(μ=0，0.3)Fig.11 Variation of stress intensity factors KⅡ, KⅢ along crack front with β (μ=0，0.3)

图10 可以看出，应力强度因子KⅡ和KⅢ绝对值均随μ的增大而减小，摩擦系数的增大可以阻碍压载引起的剪切应力所导致的断裂破坏。图11 中，μ=0，β=45°时，KⅡ和KⅢ绝对值最大，β=30°，60°时其次，并且应力强度因子曲线基本重合。在μ=0.3 时，KⅡ和KⅢ均小于μ=0 时，KⅡ和KⅢ绝对值在β=45°时仍最大，β=30°，60°时KⅡ和KⅢ绝对值其次，且曲线出现分离，这表明摩擦改变了不同裂纹倾角下应力强度因子的分布。

3.5 拉压载荷对应力强度因子影响

图12 给出了a/c=0.2，a/t=0.2，μ=0.3 时，拉伸和压缩载荷分别对应裂纹倾角β=0°，15°，30°，45°，60°，75°，90°时表面裂纹应力强度因子Ⅰ型、Ⅱ型和Ⅲ型的分量。由图12 可以看到，首先在拉伸载荷情况下，由于裂纹面张开，应力强度因子KⅠ存在，并且随裂纹倾角的增大而增大，应力强度因子KⅡ和KⅢ曲线随裂纹倾角先增大后减小，|KⅠ/Kr|max>1，而|KⅡ/Kr|<0.4，|KⅢ/Kr|<0.5，表明拉伸载荷下，随着裂纹倾角的增大，应力强度因子主要由KⅠ主导。在压载荷下，由于裂纹面闭合，KⅠ=0，应力强度因子由面内/外剪切应力所引起的KⅡ和KⅢ主导。曲线在拉伸和压载荷下沿KⅡ=0 和KⅢ=0 近似对称，且β=0°时，KⅠ、KⅡ、KⅢ均为0，表明拉伸和压载荷改变了剪切力的方向。拉载荷情况下，β=15°和30°分别与β=60°和75°重叠，而压载下由于摩擦的存在，曲线发生不同程度的分离，并且对应β下KⅡ、KⅢ绝对值均小于拉载荷的KⅡ和KⅢ。由于闭合裂纹KⅠ的缺失，导致随着β的增大，压载荷下应力强度因子KⅡ、KⅢ绝对值逐渐与拉载荷下KⅡ、KⅢ拉开差距。

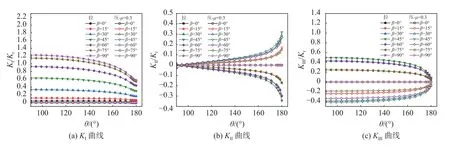
图12 拉伸/压缩载荷下，应力强度因子KⅠ，KⅡ，KⅢ随β 变化曲线Fig.12 Variation of stress intensity factors KⅠ,KⅡ, KⅢ along crack front with β under the tensile/compressive loads

3.6 侧压系数对应力强度因子影响

图13 给出了双轴压载荷下，a/c=0.4，a/t=0.8，β=45°，μ=0.3 时，侧压系数λ=0，0.25，0.5，1 对应的压载荷下表面裂纹应力强度因子Ⅱ型和Ⅲ型的分量。

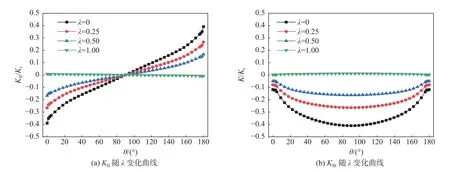
图13 应力强度因子KⅡ，KⅢ随λ 变化曲线Fig.13 Variation of stress intensity factors KⅡ, KⅢ along crack front with λ

由图13 可以看出，随着侧压系数的增大，裂纹前缘处KⅡ和KⅢ变小。在λ=1 即双轴等压时，表面裂纹应力强度因子Ⅱ型Ⅲ型分量均接近0，这点与文献[15]结论一致。表明等压条件下裂纹不会发生扩展，侧压系数的增大进一步阻碍剪切应力所导致的断裂破坏。

4 单轴压载荷下半椭圆表面裂纹应力强度因子KⅡ和KⅢ近似解

压载荷下表面裂纹应力强度因子KⅡ和KⅢ最大值分别出现于裂纹表面点处和裂纹最深点处，通过有限元求解虽然可以保证较高的精度，但是计算成本较高，不便于工程应用，所以有必要基于KⅡ和KⅢ有限元解，回归得到KⅡ和KⅢ的近似解，以便于工程评定。在裂纹面摩擦系数μ=0 情况下，受压载荷表面裂纹KⅡ和KⅢ最大，高于裂纹面摩擦系数μ>0 时的KⅡ和KⅢ。因此，本节对摩擦系数μ=0 时的应力强度因子KⅡ和KⅢ进行非线性回归，得到适于工程应用的近似解。

在经典断裂力学中，远场拉载荷作用下穿透裂纹KⅠ，KⅡ，KⅢ表达式见式（5）：

在文献[17]中，定义远场压载荷下不考虑裂纹面接触时，复合型穿透裂纹KⅠ，KⅡ，KⅢ表达式见式（6）：

根据文献[6,21]，笔者提出单轴压载下表面裂纹表面处KⅡ和裂纹深处点KⅢ近似解，具体表达式见式（7）：

由图14 可知，β=45°时，不同a/t和a/c下，通过KⅡ，KⅢ有限元与非线性拟合获得的结果误差较小。表3、4 为应力强度因子具体对比结果。

表3 裂纹表面点处KⅡ对比Table 3 Comparison of KⅡ at surface point of crack

表4 裂纹最深处点KⅢ对比Table 4 Comparison of KⅢ at deepest point of crack

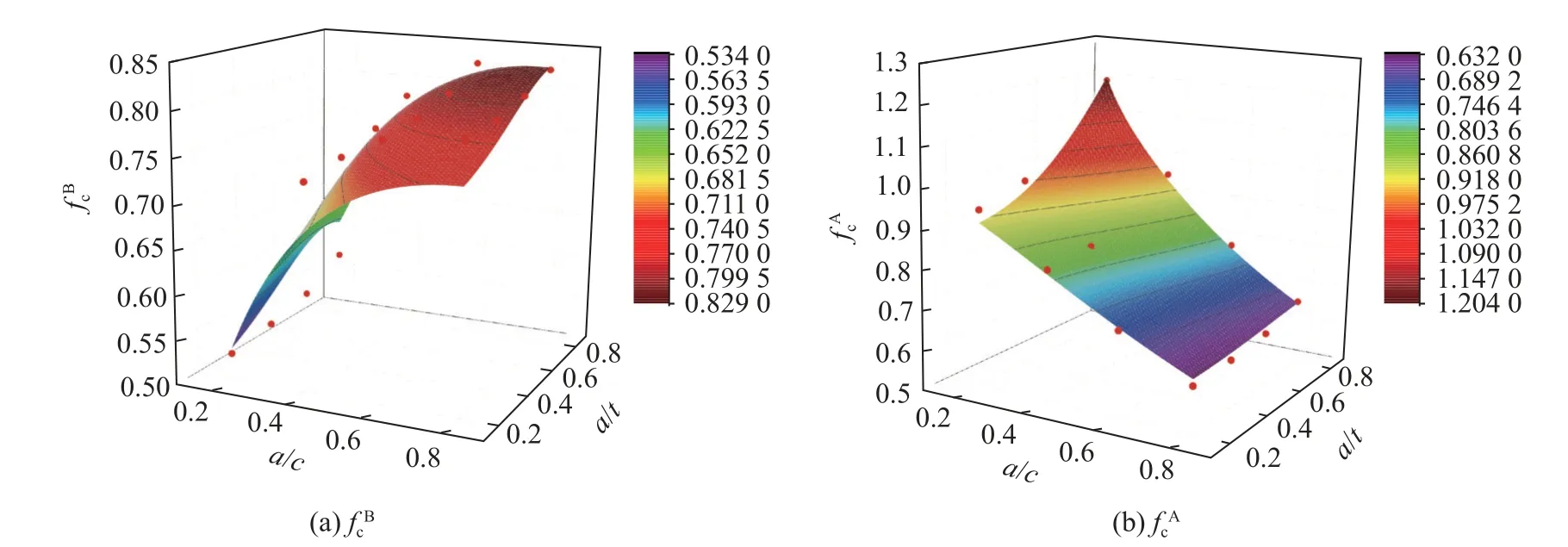
图14 拟合结果（β=45°）Fig.14 Fitted results of （β=45°）

由表3，4 可以看出，裂纹表面点KⅡ拟合结果在不同a/c时最大平均误差为6.01%，裂纹深处点KⅢ拟合结果在不同a/c时最大平均误差为2.18%，近似解与有限元数值计算所得结果较吻合，近似解对于工程评定具有参考价值。

5 结论

以工业纯钛TA2 含表面裂纹板为研究对象，分析研究了压载荷下表面裂纹应力强度因子影响因素及分布规律，进行非线性回归，得到了适于工程应用的应力强度因子KⅡ和KⅢ近似解。结论如下：

1）压载荷下，表面裂纹应力强度因子KⅡ和KⅢ分别关于θ=90°呈反对称和对称分布。β<45°时，KⅡ和KⅢ绝对值随β增大而增大，在β=45°时取得最大值；β>45°，KⅡ和KⅢ绝对值随β增大而减小。表面裂纹KⅡ和KⅢ随a/t增大而增大，a/t对应力强度因子影响较弱。表面裂纹随a/c的增大由KⅢ主导逐渐变为KⅡ主导，KⅡ、KⅢ对于a/c影响变化较敏感。

2）压载荷下，表面裂纹应力强度因子KⅡ和KⅢ绝对值随摩擦系数μ，侧压系数λ增大而减小，μ和λ可明显改善闭合裂尖应力分布，抑制剪切力导致的断裂破坏；压载荷下，表面裂纹应力强度因子KⅠ=0，KⅡ和KⅢ曲线在拉伸和压缩载荷下沿KⅡ=0和KⅢ=0 近似对称；由于闭合裂纹KⅠ的缺失，导致随着β的增大，压载荷下应力强度因子KⅡ、KⅢ绝对值逐渐与拉载荷下KⅡ、KⅢ拉开差距。

3）基于应力强度因子有限元解，通过非线性回归，得到了单轴压载荷下表面裂纹KⅡ和KⅢ近似解。研究结果对工业纯钛TA2 含表面裂纹结构安全评价具有参考价值。