研究中考真题 明晰考查方向
文/陆丽萍

圆,作为几何图形的基本图形之一,是中考数学的重要考查对象。本文精选了2022 年与圆相关的中考真题,从考查方向、呈现形式、设问出发,对命题趋势做些思考,希望对同学们的备考有所帮助。
一、圆周角定理及其推论
圆周角定理及推论以“弧”为中介,把圆中的角联系起来,可用来求角的度数以及证角相等,单独考查时会出现在选择题、填空题中,与其他知识结合时多出现在综合解答题中,是中考必考内容。
例1(2022·江苏苏州)如图1,AB是⊙O的直径,弦CD交AB于点E,连接AC、AD。若∠BAC=28°,则∠D=______°。
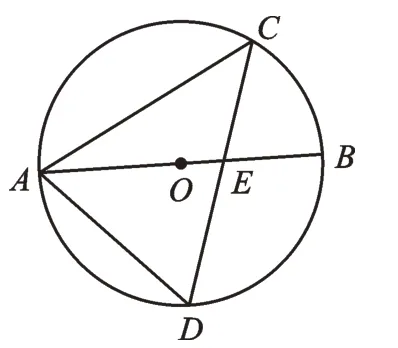
图1
【解析】如图2,连接BD,根据直径所对圆周角是90°,可得∠ADB=90°。由圆周角定理得∠BDC=∠BAC,进而可得∠ADC=90°-∠BDC=62°。故答案为62。
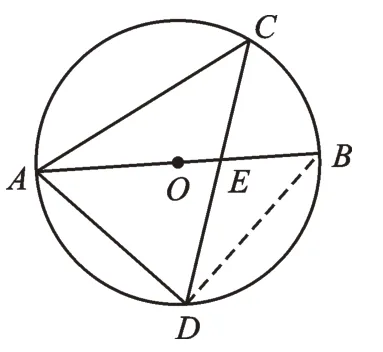
图2
【点评】本题考查了同弧所对的圆周角相等,直径所对的圆周角是直角,掌握圆周角定理及其推论是解题的关键。
二、切线的判定与性质
切线的判定与性质是中考热点,考查题型设置广泛,但处理方法并不复杂。
例2(2022·江苏扬州)如图3,AB为圆O的弦,OC⊥OA交AB于点P,交过点B的直线于点C,且CB=CP。试判断直线BC与圆O的位置关系,并说明理由。
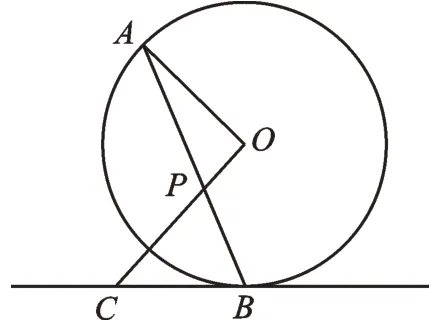
图3
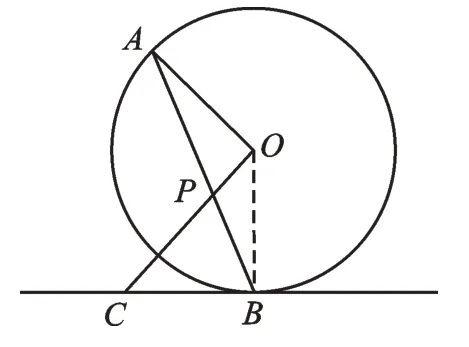
图4
【解析】连接OB,根据等腰三角形的性质得出∠A=∠OBA,∠CPB=∠CBP,求出∠OBC=∠AOC=90°,再根据切线的判定得出结论。
【点评】判定一条直线是圆的切线时,若直线与圆的公共点已知,证明方法是“连半径,证垂直”;若直线与圆公共点未知,证明方法是“作垂线,证半径”,证圆心到直线的距离等于圆的半径(即证d=r)。
例3(2022·江苏盐城)如图5,AB、AC是圆O的弦,过点A的切线交CB的延长线于点D,若∠BAD=35°,则∠C=______°
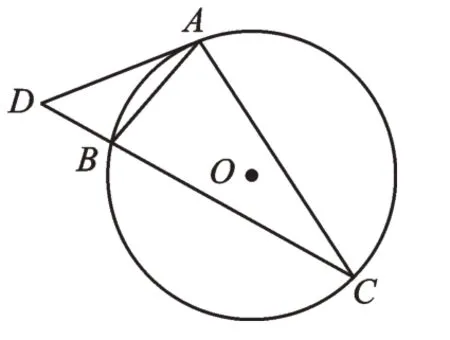
图5

图6
【解析】连接AO并延长,交圆O于点E,连接BE。根据圆周角定理可得∠E+∠BAE=90°,再根据AD为⊙O的切线,可得∠BAE+∠BAD=90°,可得∠E=∠BAD=35°。最后根据圆周角定理即可求得∠C=∠E=35°。故答案为35。
【点评】如果我们要运用切线的性质来解决问题,常见作辅助线的方法是连接圆心和切点,再利用垂直构造直角三角形。
三、弧长、扇形面积与圆锥侧面积的计算
弧长、扇形面积、圆锥侧面积的计算重在明晰公式中字母的各自指代,如此才能灵活运用公式进行计算。
例4(2022·江苏盐城)如图7,在矩形ABCD中,AB=2BC=2,将线段AB绕点A按逆时针方向旋转,使得点B落在边CD上的点B'处,线段AB扫过的面积为______。
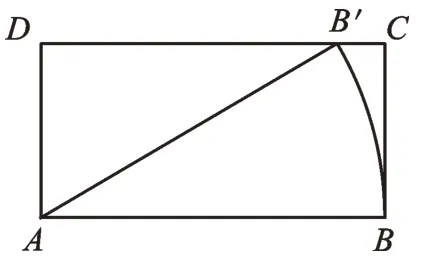
图7
【解析】由旋转的性质可得AB'=AB=2,由锐角三角函数可求出∠DAB'=60°,从而得出∠BAB'=30°。由扇形面积公式,得线段AB扫过的面积=故答案为
【点评】本题主要考查了旋转的性质、矩形的性质、扇形面积公式、锐角三角函数等知识,通过旋转构建图形并运用合适的公式是解决此题的关键。
解决圆的问题,我们要熟悉图形的性质与判定,能从复杂图形中分离出基本图形。这种化繁为简的处理策略是解决问题的一种有效途径。

