基于PageRank 传播机制的超图神经网络
刘彦北,周敬涛
(天津工业大学电子与信息工程学院,天津 300387)
图的应用是非常广泛的,现实生活中处处是图的场景。近些年,图神经网络的方法得到了广泛的关注,以传统图结构为基础,在图表示学习方面取得了很大的成果。然而随着图神经网络应用的不断扩展,传统图结构定义的点与点成对关系已经无法满足描述现实情况中数据之间高阶复杂关系的要求,传统图表示学习在消息传递方面也面临挑战。
相对于普通图而言,超图可以更加准确地描述存在多元关联的对象之间的关系。超边构建非成对关系,因此,超图很适合用于描述高阶数据相关性,同时在学习多模态和异构数据上都有建树。超图学习最早由Schölkopf 等[1]提出,用于处理超图结构,减小超图上连接性紧密点的标签的差异。Metaxas 等[2]提出超图学习被应用于视频对象分割任务。Huang 等[3]利用超图结构对图像关系进行建模,并且对图像排序进行转导推理。Gao 等[4]引入l2 正则化来学习最优超边权值。Hwang 等[5]通过假设高度相关的超边缘应该具有相似的权重,进一步探讨了超边缘之间的相关性。之后Gao等[6]引入了多超图结构,并且为不同的子超图分配不同的权重,以此在处理多模态数据的基础上应对不同的模式。Jiang 等[7]提出了动态超图神经网络DHGNN,由动态超图构造(DHG)和超图卷(HGC)2 个模块构成,通过不断更新超图结构来最终达到最贴切数据的学习表示。Bai[8]在图神经网络中引入了2 个端到端的可训练操作内容,即超图卷积和超图注意,用于有效学习高阶图结构数据上的深度嵌入。Feng 等[9]设计了一种超边缘卷积,在超图神经网络HGNN 中学习高阶数据相关性。Zhang 等[10]开发了一种新的基于自注意的图神经网络,称为Hyper-SAGNN,适用于具有可变超边大小的同质和异质超图。Xia 等[11]将超图网络与自监督学习相结合并应用于会话推荐任务。Lee 等[12]采用个性化的重加权方案进行节点跳跃,通过概率的形式重新解释超图上的随机游走概念。
传统的消息传递算法是在图神经网络上展开的。文献[13-14]提出了谱图卷积神经网络;文献[15-16]提出了消息传递算法;Dai 等[17]通过递归神经网络进行邻居聚合;Veliˇckovic'等[18]在图神经网络的基础上引入了注意机制;AbuElHaija 等[19]提出了随机游走;Gilmer 等[20]使用了边缘特征;文献[21-24]试图增加跳跃的连接步数来改进传统的消息传递算法;Xu 等[25]将消息传递与聚合方案相结合。然而,上述工作的消息传递层数依然是有限的。Li 等[26]通过合作训练和自我训练相结合的方式来促进模型训练。Eliav 等[27]也有类似的表现,取得的改进效果接近于其他的半监督分类模型。文献[28-29] 通过结合残差连接和批量归一化避免了过拟合问题。Gaseiger[30]使用图像卷积的关系网络(GCN)和网页排名得出一种改进的传播方案即基于个性化的网页排名。Sun 等[31]利用将AdaBoost 与网络合并的方法,构建新图卷积网络AdaGCN,从根节点的高阶邻居中提取信息。综上所述,超图学习需要在增大学习领域范围的同时,保持对根节点的适当关注。
本文提出了一种使用个性化网页排名PageRank代替传统邻居聚合的传播方案,该算法增加了传播过程传回根节点的概率,PageRank 算法在对根节点的局部领域进行编码时,能够在扩大学习领域的同时保持对根节点信息的关注。模型的传播方案允许网络层数逐渐增多,理论上可以接近无限多层,而且不会导致过平滑。除该优势之外,本算法当中的传播算法与神经网络独立存在,因此,可以在不改变原有神经网络的基础上来实现更广的传播范围,使模型具有一定的推广性。与前人所述PageRank 与传统图卷积网络方法相结合的算法PPNP[30]相比,本文提出的算法是将PageRank与超图卷积网络相结合克服各自局限性的模型HGNNP,优势在于:利用超图适合处理数据之间高阶关系的特点,有效学习根节点周围更多类型的连接信息;使用PageRank 思想在根节点周围实现更广的学习领域,同时不丢失根节点本身的信息。为验证所提出的HGNNP 算法的有效性,本文进行了视觉对象分类任务实验,并与目前流行的方法相比较,以期能够在较深的卷积网络层数下较好地处理多模态数据的高阶关系。
1 模型及方法
本文模型HGNNP 将超图神经网络与个性网页排名相结合,包含超图构建、超图卷积网络、个性化网页排名机制等内容。
1.1 超图构建
超图学习是一个很宽泛的概念,其中最基础的是超图构造。通常情况下,超图被定义为G=(V,E,W)。其中:节点集为V,包含了超图上所有的顶点;超边集为E,包含由任意个关联顶点构成的边;W 则是由每条超边的权重构成的权重集,是由超边权重构成的对角矩阵;而超图的关联矩阵H 可以由|V|×|E|来表示;对于任何一个属于V 的节点v 而言,节点的度被定义为d(v)=h(v,e);对于一个属于E 的超边e而言,边的度被定义为δ(e)=;那么很显然,De和Dv表示超边度和节点度的对角线矩阵。
普通图描述的是边和成对节点之间的关系,超图的关联矩阵描述的是超边与节点之间的关系。特殊情况下,当超图中所有的超边包含的节点个数都为K 个时,称该超图为K 均匀超图。还应当注意的点是,在超图构建的过程中,即使超边所包含的点个数是相同的,超边的类型也会因为所包含节点类型的不同而不同,从这里也能看出超图适用于处理多模态数据。
1.2 超图卷积网络
超图卷积网络(HGNN)是在构建超图的基础上捕捉节点之间的高阶关系,是由传统图卷积网络发展而来的。
首先回顾下普通图的卷积网络(GCN),传统的GCN网络如式(1)所示:
对于超图卷积网络而言,输入网络数据集通常分为训练数据集和测试数据集。在输入网络时,与传统图相同的地方是都使用了最初始的数据特征,不同的地方在于关联矩阵的形成。超图利用多模态数据集的复杂相关性构造了很多超边缘结构群,通过超边生成的方式(hyperedge generation)将其连接起来,进而生成邻接矩阵H,然后将新生成的邻接矩阵与节点特征输入超图神经网络,得到最后的标签特征。由此可知,一个超边卷积层的公式为:
式中:X(l+1)代表第l+1 层节点的特征;σ 代表非线性激活函数。超图神经网络基于超图上的谱卷积,在式(2)中实现了节点—边—节点特征的转换,利用超边特征聚合和邻居节点特征融合,捕捉节点数据之间的高阶相关性。其中,滤波器矩阵θ(l)与初始的节点特征X(l)相乘进行滤波处理,改变特征的维度;然后根据超边的特性,将节点特征汇聚成超边特征,这一步骤通过与的乘法实现;然后以乘以关联矩阵He的方式,将与根节点相关的超边特征重新汇聚成节点特征,Dv和De起到归一化的作用;最后通过非线性激活输出最终结果。
在超图神经网络中,超图构造首先要考虑超边的构建,如图1 所示,网络模型根据节点之间的距离来构造关联矩阵,进而形成超边。普通图中,边只考虑两点之间的联系,而超边衡量了多个节点之间的关系。

图1 超边生成Fig.1 Hyperedge generation
1.3 网页排名机制PageRank
PageRank 来源于网页链接之间的随机游走机制,使用户可以点击链接跳转到新的页面,不至于一直在本网页停留,也不至于链接不到新的网页,使用户可以一直浏览自己所感兴趣的网页内容,类似于学习到了用户的兴趣范围,其传播机制如图2 所示。

图2 PageRank 传播机制Fig.2 Propagation mechanism of PageRank
由图2 可知,对于根节点x1来说,信息的传播在相连的节点之间进行,从一个顶点到下一个顶点游走的过程中,有α 的概率回归它本身,有1-α 的概率传递给x2、x3、x4,同时下一次传递时,这3 个顶点也是有α 的概率传回x1。这个传播过程是以x1为重心的,即以它作为本次传播的根节点,最终学习到的信息为该节点的信息表示。
如前文提到的,可以利用网页排名机制PageRank来避免根节点信息的丢失。为了更方便快速地实现本模型的设计目的,引入一个PageRank 的变体,即将根节点考虑在内的个性化PageRank。与普通的网页排名机制不同,个性化PageRank 是针对个人而言的PageRank,每次重新游走的时候,都是从根节点用户节点u 开始,在学习节点u 的信息时,该节点初始化为1,其他节点初始化为0。
个性化PageRank 的进阶公式为:
式中:ix为根结点特征向量;为加上归一化以及自循环的邻接矩阵;πppr(ix)为传播之后的特征;α 为传播概率。在这里,先将网页排名机制与图网络的传播过程联合在一起,得到的公式为:
式中:X 为特征矩阵;fθ(x)为参数为θ 的对数据特征进行预处理的神经网络。由式(5)可知,对节点标签进行预测的神经网络与传播机制是分割开来的,神经网络的结构以及层数深度是独立于传播算法存在的。由此可以灵活地改变模型中神经网络的模型,可以用任意的传播矩阵来替换式(5)的。本文对式(5)使用了简便的形式以降低模型的计算复杂度。此外HGNNP模型训练是端到端的。
1.4 基于PageRank 算法的超图神经网络
HGNNP 模型如图3 所示。

图3 HGNNP 模型示意图Fig.3 Schematic diagram of HGNNP model
由图3 可知,初始数据经过超边聚集(hyperedge generation)生成超图的关联矩阵H,该关联矩阵描述的是超边与它包含的多个节点之间的连接信息,通过该方法生成了不同于传统图的“连接信息”。神经网络的输入不仅需要连接信息,还需要节点的属性信息。因此,将生成的关联矩阵H 与原始的节点特征共同输入超图神经网络。该网络的作用就是利用超图以及超边的特性来对原始的节点特征进行重新表示学习。
具体步骤为输入的节点特征利用关联矩阵中超边与节点的关联信息,依据超图神经网络的网络模型(hypergraph neural networks),经过一层点—边—点的特征变化过程,不断迭代更新以得到最终的学习表示,其中“边”指的是超边特征。节点特征经过节点特征转换、超边特征聚合、节点特征聚合过程得到新的节点学习表示,再经过非线性激活函数,最终得到初始嵌入节点特征hi。在初始嵌入节点特征基础之上,使用个性化PageRank 机制进行信息传播,吸收周围邻居节点的信息;同时以一定的概率回到根节点本身,每经历一层的信息传播之后,再进入超图神经网络进行下一次特征学习,直到得到最终学习表示。
具体来讲,处理之后的节点特征结合PageRank进行信息传播,该传播机制使得节点信息有α 的概率传回本身,有1-α 的概率再次进入超图神经网络中,正是这个概率保证了一定程度上可以再次汇聚根节点本身的信息,防止在吸收周围的邻居节点信息时学习范围过广或层数过深使得根节点的信息被丢失掉。因此,使得模型能够在有效吸收周围邻居节点信息的同时,一定程度上保留根节点的信息。
上述过程有效地防止了模型层数过深时过拟合、节点学习表示趋近于稳定值和模型泛化能力弱的情况。具体表现为,当学习层数过深时,节点的学习表示会趋向该图的极限分布,节点表示不再取决于根节点和其周围的邻居信息,而取决于整个图本身,而模型使用的网页排名机制解决了这个问题。
本文模型结合超图神经网络和网页排名机制,得到HGNNP 的整体公式:
式中:X(l+1)为下一层的节点特征;α 为传播概率;Dv和De为节点和超边的度矩阵,起到了归一化的作用;X(0)不是初始的节点特征,而是经过超图神经网络预处理之后的节点特征hi;其余字符含义不变。
对比超图神经网络,HGNNP 每一次传播不是直接传播到相邻节点,而是有α 的概率回归到本身,本质上传播机制发生了改变。对比PageRank 算法和传统图网络结合的方法,神经网络模型引入了超图和超边的概念,根本区别是卷积网络中的连接信息发生改变,多个节点相连的超边的存在使得节点表示学习中节点信息学习得更为全面准确。
综上所述,HGNNP 将超图神经网络与PageRank算法相结合,不仅解决了传统图学习算法无法处理的高阶数据相关性的问题,而且可以利用特定的传播机制加深模型的网络层数,以使网络模型更全面更准确地学习节点的信息,在处理分类问题和预测问题时,实验效果会更好。
2 实验和结果
2.1 数据集和实验设置
为了验证本文所提出的HGNNP 模型,实验利用了2 个视觉对象分类的数据集,包括普林斯顿大学的ModelNet40 数据集以及台湾大学的NTU 3D 模型数据集。表1 为2 个数据集的节点种类个数、训练和测试的节点个数以及总共的节点个数。需要注意的是,ModelNet40 数据集由来自40 个流行类别的12 311 个对象组成,并应用了相同的训练/测试分割。其中,9 843 个物体用于训练,2 468 个物体用于测试。NTU数据集由来自67 个类别的2 012 个3D 形状组成,包括汽车、椅子、国际象棋、芯片、时钟、杯子、门、框架、笔、植物叶等。在NTU 数据集中,80%的数据用于训练,其他20%的数据用于测试。本实验采用2 种提取特征的方法MVCNN(用于3D 形状识别的多视图卷积神经网络)和GVCNN(用于3D 形状识别的群视图卷积神经网络)在该三维模型数据集上提取特征,这2种方法在三维对象表示上有着非常好的性能表现。

表1 ModelNet40 和NTU 数据集的详细信息Tab.1 Detailed information of ModelNet40 and NTU datasets
为了与传统图神经网络做对比,利用节点之间的距离来构建图结构。在构造超图步骤时使用2 种方法:一种是依据KNN(K 最邻近分类算法)思想选取10个离根节点最近的点构成超边,进而构建超图;另外一种是在数据特征呈现多模态时,构建超图关联矩阵,并将多个不同属性特征的关联矩阵拼接在一起,构成多模态特征的超图。
在上述2 个数据集完成半监督分类实验的基础之上,对传播概率α 和传播层数N 进行控制变量和消融实验,以更直观地判断出2 个超参数对模型效果的影响。
2.2 半监督分类
在ModelNet40 和NTU 数据集上分别实现半监督分类实验,评价标准主要是分类的准确率。其中,每一个数据集在提取特征时都使用MVCNN 和GVCNN 这2 种方法,这2 种方法皆可用于构建超图或者提取特征。实验针对不同条件进行分类讨论,将2 种卷积方法分别用于构建超图以及提取特征。
用直方图直观地表明本文模型效果的提升,如图4 所示,并对比不同参数条件下2 个数据集的实验效果。如不做特殊说明,G+M 表示GVCNN 和MVCNN相结合;G+M_G 表示在构造超图时使用GVCNN 和MVCNN 提取的特征,在训练网络时使用GVCNN 提取的特征这一实验情况,其他的类比即可。

图4 不同参数条件下2 个数据集上的分类结果比较Fig.4 Comparison of classification results on two data sets with different parameters
由图4 可知,在NTU 数据集上,与其他模型相比,HGNNP 多数实验条件下分类效果是最好的,提升的程度比较大,最高准确率达到85.79%,与HGNN 相比,提高了8.59%;在ModelNet40 数据集上,与其他模型相比,HGNNP 模型性能较好,最高准确率达到了93.07%,但由于ModelNet40 与NTU 数据集相比数据样本偏少,HGNNP 模型的提升效果不明显,与HGNN 相比,提高了0.47%。综上所述,与HGNN 相比,HGNNP在多数情况下提升效果显著,由此验证了本文模型的有效性和稳定性。个别情况效果比较差,原因是实验条件中用于构建超图的特征和用于学习的特征之间存在差异,深度网络使差异明显化,因此,在准确率上会有一定的误差。
2.3 参数分析
为分析传播概率α 对于模型的影响,本文将所有情况下针对α 在[0.01,0.2]区间内的分类结果进行展示,如图5 所示,以探求α 取何值时模型效果取得最优。
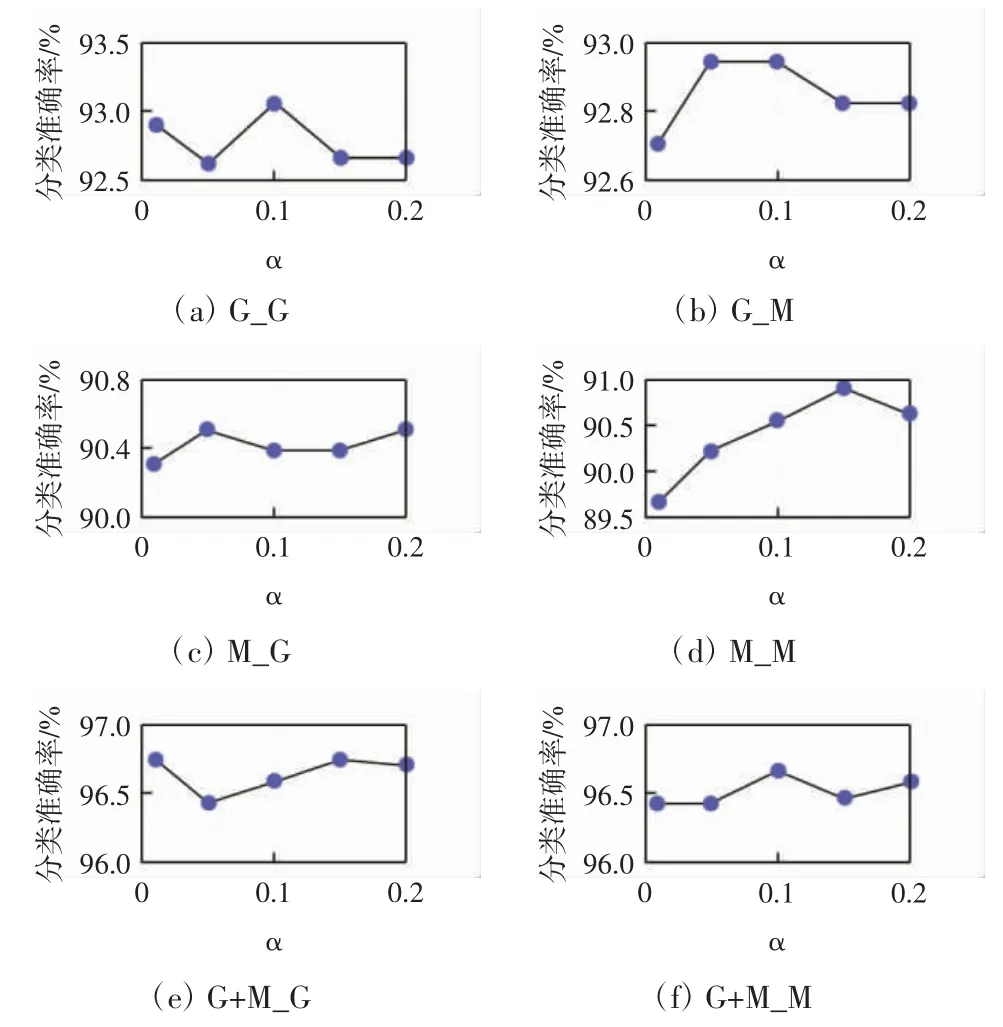
图5 HGNNP 在ModelNet40 数据集上随α 的变化Fig.5 Changes of HGNNP with α in ModelNet40 dataset
由图5 可以看出,在ModelNet40 数据集上HGNNP随α 的变化趋势。一开始在0.1 处准确率比较低,也就是说当接近以往的传播机制,没有概率传回根节点本身时,准确率会比较低;在0.1~0.15 之间,准确率达到最高,说明在这一范围内调节α 可以得到最优模型。这也验证了对根节点信息进行一定的保留比直接传播学习的信息更全面准确。在NTU 数据集上也可以发现类似的规律,本文不再赘述。传播概率α 对HGNNP模型效果影响显著,传播层数N 在模型中也是重要的影响参数。HGNNP 在Model-Net40 数据集上的分类效果随N 的变化如图6 所示。

图6 HGNNP 在ModelNet40 数据集上随N 的变化Fig.6 Changes of HGNNP with N in ModelNet40 dataset
由图6 可知,传统的卷积神经网络在层数过深时会出现过拟合的现象,而本文模型在层数过深时依然可以保持稳定的分类准确率,并且随着层数的加深,存在一个临界值使得模型分类效果最优。本文模型在传播层数较少时准确率较低,传播层数接近1 时模型上近似于传统的神经网络;随着传播层数的加深,分类准确率逐渐上升,在传播层数为2~5 之间时逐渐达到最大值;之后会逐渐地下降。同等意义上,对于本文模型来说,使用网页排名的传播机制传播5 层左右,可以使HGNNP 达到最优。
更为重要的是,当传播层数逐渐加深到一定程度时,HGNNP 表现趋于稳定,不再出现大幅度的变化,甚至当接近无限的网络层数后,模型表现依然不会出现很大的变化,不会因为过平滑的问题而分类错误,这正对应了前文提到的要解决的挑战和问题,验证了本文模型相比传统神经网络的优越性。
3 结论
本文针对传统超图神经网络卷积过程中层数过深过拟合以及传播范围小的问题,提出了一种基于PageRank 传播机制的深度超图神经网络HGNNP。实验结果表明:与传统的深度图神经网络相比,HGNNP在各种学习任务中都可以取得较好的性能。其中在ModelNet40 数据集上,最高准确率达到了93.07%,相比HGNN 提高了0.47%;在NTU 数据集上,最高准确率达到了85.79%,相比HGNN 提高了8.59%。

