考虑尖点突变理论的边坡安全稳定性综合评价

廖元欢,邓 涛,李 得,庞 鑫,秦 梨,周 成,张成良*

(1.昆明理工大学 国土资源工程学院,云南 昆明 650093;2.攀钢集团矿业有限公司设计研究院,四川 攀枝花 617063)

边坡作为岩土工程领域一个较为关注的问题,因边坡引起的滑坡、泥石流等地质灾害突出,边坡的稳定性直接影响着工程进度和国民生产安全[1-4],特别是对公路、露天矿山等大型边坡产生的边坡滑坡和失稳会造成重大损失[5],因此研究边坡稳定性具有重要意义。当前边坡稳定性分析方法主要包含极限平衡法和强度折减法[6]等,其中强度折减法需要面对的问题就是失稳状态判据的选择。目前已有位移突变、塑性区贯通、数值计算不收敛、剪切应变贯通等作为判断依据,但由于人为因素的影响存在的差异,这些判据并未使失稳判据进行量化;而极限平衡法不能分析边坡的演化过程,只能求解整体稳定性系数。突变理论[7]作为一种非线性分析方法可以有效考虑不连续破坏过程,在很多工程已经得到应用,特别是对有多种因素影响的边坡,可以很好地解释其破坏过程。近年来,许多学者对边坡稳定性做了相关研究。周子涵等[8]基于突变论建立了用于判定边坡失稳的能量突变判别准则,并且在考虑安全系数的情况下表明能量突变趋势与安全系数在开挖次数下具有一致性。李志平等[9]基于尖点突变理论建立以折减系数为控制变量,塑性区应变为状态变量的突变模型,以此表征塑形应变能的变化过程。赵旭等[10]考虑地震荷载响应下建立折减系数与塑性区应变的突变模型,计算所得安全系数最大误差仅为3%。史俊涛等[11]基于突变理论建立了非均质土边坡的数值失稳突变模型,极大克服了人为因素误差使结果更加客观。因此,尖点突变理论-强度折减法在自然工况下的边坡稳定性分析中已经有所应用,然而对于地震工况下尖点突变理论-强度折减法的应用虽然在隧道的稳定性中有研究,但对于边坡动力稳定性分析并未有过多研究。

综上,本文运用FLAC3D有限元分析软件,基于尖点突变理论-强度折减法,建立强度折减系数与边坡监测位移的尖点突变理论位移突变数学模型,判断边坡失稳情况,实现失稳判据的量化,并结合强度折减法、极限平衡法计算该边坡在自然工况、地震荷载[12]作用下的边坡失稳情况,通过分析对比判断边坡的最终稳定性情况,为边坡稳定性分析提供一个新思路,并对后期边坡支护提供指导。

1 基本原理

1.1 强度折减法

强度折减法[13]是通过有限元软件建立的数值分析模型,对模型自身抗剪强度参数,黏聚力、内摩擦角,持续进行折减,直至模型达到破坏条件,所得折减系数即是安全系数,如下所示:

(1)

式中:C、C′ 分别为岩体折减前后的黏聚力;θ、θ′分别为岩体折减前后的摩擦角;F为折减系数。运用强度折减法进行安全技术计算时,首先要确定合理的失稳判定准则。

1.2 尖点突变理论

突变理论[14]作为一种非线性分析方法,能很好地解释系统突变的这一过程,有助于理解系统变化和中断。尖点突变理论作为一种解决不连续突变问题的方法,因其几何直观性强,已广泛应用于边坡稳定性评价和抗震性分析,其势函数为

V(u,v,x)=x4+ux2+vx

(2)

式中:u、v为控制变量;x为状态变量。若V′(x)=0,可求得其平衡方程为

V′(x)=4x3+2ux+v

(3)

一个三维连续曲面的平衡曲面和控制平面如图1所示。曲面可分为下叶、中叶、上叶3个部分,形成1个弯曲折叠的曲面,上叶、下叶为平衡稳定点、中叶处于失稳状态。对V′(x)求导可以得到奇点集满足

图1 平衡曲面和控制平面Fig.1 Equilibrium surface and control plane

V″(x)=12x2+2u=0

(4)

结合式(3)和式(4),可得突变理论的判别方程为

Δ=8u3+27v2

(5)

此为尖点突变理论失稳的判别方程。

1.3 边坡尖点突变理论位移失稳判定模型建立

边坡的失稳通常可以认为是一个突变的过程,因此,运用强度折减法计算时可以得到各强度折减系数下位移的突变情况,即强度折减系数与位移的函数关系f(k),构建强度折减系数-位移突变数学模型。在计算过程中,以折减系数作为控制变量,位移作为状态变量构建折减系数位移方程,对其进行4次Taylor级数展开如下:

V(x)=f(k)=c0+c1k1+c2k2+c3k3+c4k4

(6)

式中:ci(i=0,1,…,4)为拟合参数;k为边坡折减系数。

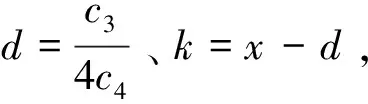
V(x)=b4x4+b2x2+b1x+b0

(7)

bi与ci关系如下:

b0=d4c4-d3c3+d2c2-dc1+c0

b1=-4d3c4+3d2c3-2dc2+c1

b2=6d2c4-3dc3+c2

b4=c4

(8)

对式(7)等式两边同时除以b4可得其标准式

V(x)=x4+ux2+vx+c

(9)

其中:

式中,c为常数。

依据尖点突变理论的失稳判定原理,可得边坡失稳的突变特征值为

Δ=8u3+27v2

当Δ=8u3+27v2>0时,表示边坡稳定;当Δ=8u3+27v2<0时,表示边坡失稳;当Δ=8u3+27v2=0时,表示边坡处于临界状态。 因此,突变特征值可判定在不同折减系数下边坡的稳定性情况。

2 工程概况

某工程边坡位于滇西南地震带的澜沧—耿马次级地震带内,区内历史上发生过多次破坏性地震。边坡呈折线形,长100 m,高40 m,主要为中风化砂岩。目前该边坡并未进行分台削坡减载和平台修整,根据工程地质测绘结果,斜坡现状稳定性较好。边坡数值计算剖面图如图2所示。

图2 边坡数值计算剖面图Fig.2 Slope numerical calculation profile graph

3 数值分析

为说明突变理论-强度折减法建立的位移尖点突变理论数学模型的合理性,运用Rhino-Griddle-FLAC3D联合建立边坡数值计算模型,如图3所示。模型X轴100 m,Z轴60 m,Y轴10 m,坡高40 m;计算过程中固定四周及底部边界,计算服从摩尔库伦本构数值计算模型。岩土体物理力学参数如表1所示。

图3 边坡数值计算模型Fig.3 Numerical calculation model for slopes

表1 岩土体物理力学参数Tab.1 Physical mechanics parameters of rock and soil mass

3.1 稳定性计算分析

通过FLAC3D内置fish语言编写强度折减法程序,以初始折减系数F=1.05对边坡进行强度折减计算。当F=1.67时,计算收敛;当F=1.68时,计算不收敛,位移严重失真,此时认为边坡安全系数为1.67。不同折减系数下剪切应变云图如图4所示。由图4可以看出:当F=1.65时,最大剪切应变未贯通;当F=1.66时,最大剪切应变贯通,因此判定此时的边坡安全系数为1.65。

(a)F=1.65 (b)F=1.66图4 剪切应变云图Fig.4 Shear strain contour

3.2 尖点突变理论的位移失稳判定分析

FLAC3D对边坡进行强度折减法计算过程中,对不同折减系数情况下边坡位移进行监测,构建折减系数与位移的尖点突变理论失稳判定数学模型。运用Origin软件对其进行四次多项式拟合,拟合结果如图5、表2所示。由图5和表2可知:当F=1.65时,Δ>0;当F=1.66时,Δ<0,因此确定此时的边坡安全系数为1.65。当折减系数大于1.65时,边坡处于失稳状态;随着折减系数的减小,突变特征值呈现一种增大的趋势,此区域即是安全区域。

图5 位移与强度折减系数的拟合曲线Fig.5 Fitting curve of displacement to intensity reduction factors

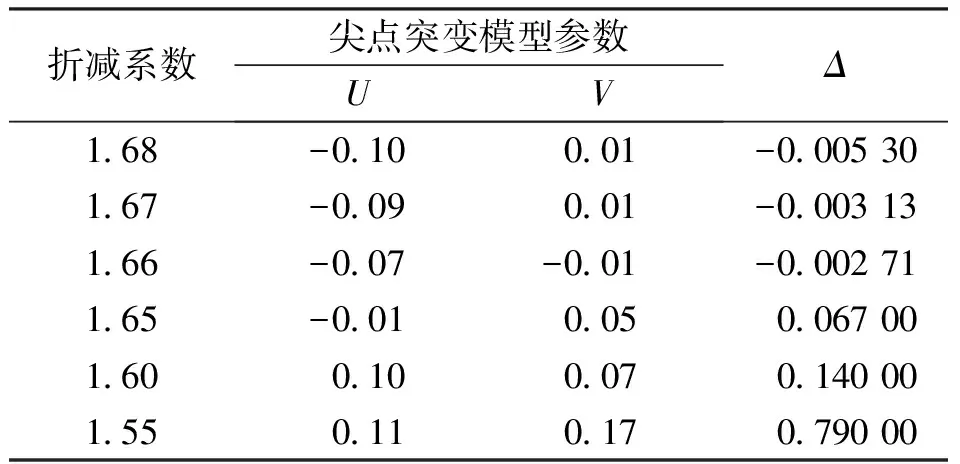
表2 不同折减系数突变特征值Tab.2 Mutation characteristic values of different reduction coefficients

3.3 抗震性分析

为研究地震载荷作用下边坡失稳状况,运用FLAC3D对边坡进行抗震性分析。模型采用摩尔库伦本构,四周施加自由场边界,底部施加静态边界,阻尼设为局部阻尼,选用EI波,加速度0.2g,加速度时程曲线图如图6所示。动力计算过程中,在底部施加水平方向0.3g、竖直方向0.2g的加速度时程,采用fish语言的动力强度折减法对边坡进行折减计算。因计算过程中动力计算的特殊性,计算不收敛不能作为在地震工程的失稳判据准则。

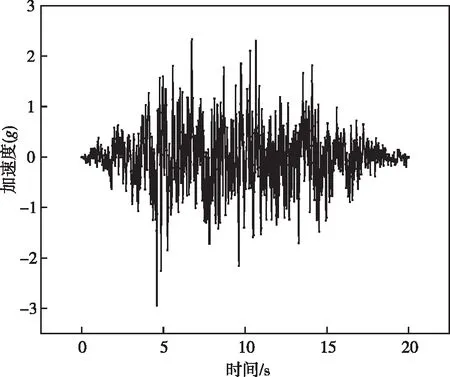
图6 加速度时程曲线Fig.6 Acceleration time-history curve

3.3.1塑性区分析

动力计算过程中,边坡为了维持自身稳定性,塑性区会不断变化。当F=1.22时,边坡塑性区云图如图7(a)所示,边坡塑性区贯通,边坡发生破坏;当F=1.21时,边坡塑性区云图如图7(b)所示,边坡塑性区未贯通,此时确定边坡安全系数为1.21。图7中,n表示正在发生破坏,p表示过去发生破坏现在处于稳定状态。根据fish塑性区体积计算程序计算不同折减系数下塑性区体积,如图8所示。由图8可知:v_tension_now在折减计算过程中变化平稳,v_tension_past随折减系数增大而减小;v_shear_now随着折减系数增大不断增大,v_shear_past随折减系数增大而增大。在折减系数为1.2时,v_shear_now出现拐点急速增加,结合塑性区贯通,综合判定此时的边坡安全系数为1.21。

(a) F=1.22 (b) F=1.21图7 边坡塑性区云图Fig.7 Cloud map of slope plastic zone

图8 不同折减系数与塑性区关系Fig.8 Relation between reduction factors and plastic zones

3.3.2位移分析

在地震作用下,边坡监测点破坏严重,随着折减系数增大边坡位移增大,坡顶最大竖直方向位移为154.28 mm,坡趾最大水平位移为165.89 mm,如图9所示。由图9(a)可以看出:当F=1.2时,水平位移发生突变,位移增速变大;而图9(b)中,位移随F增大而增加,但并未发生明显的位移突变情况,因此选择坡趾监测点水平位移用于位移突变分析数据源。

图9 地震作用下不同折减系数监测点位移Fig.9 Displacement of monitoring points with different reduction coefficients under earthquake

3.3.3基于尖点突变理论的动力强度折减法位移突变分析

在地震荷载不断作用下,边坡位移会随着加速度载荷的改变而变化,取一段时间载荷作用下的位移进行位移突变是可靠的。地震载荷下不同折减系数突变特征值如表3所示。由表3可知:当F=1.21时,Δ>0,边坡在地震加速度载荷作用下处于稳定状态;当F=1.22时,Δ<0,边坡在地震加速度载荷作用下处于失稳状态。根据尖点突变理论失稳判定准则,此时边坡的安全系数为1.21。

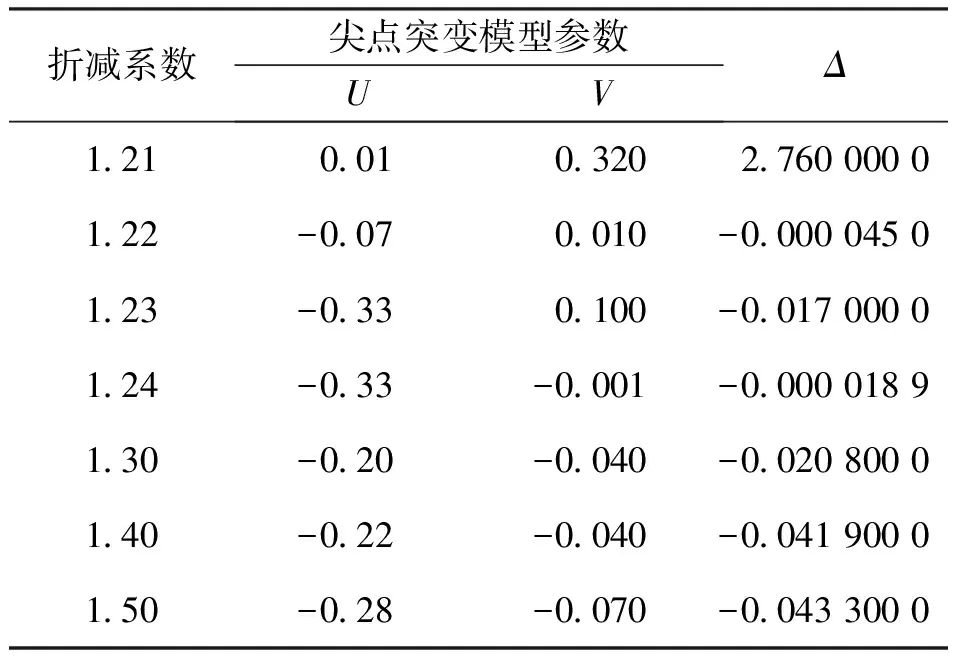
表3 地震载荷下不同折减系数突变特征值Tab.3 Mutation characteristic values of different reduction coefficients under seismic load

3.4 各失稳判据对比分析

在自然、地震2种工况下,将极限平衡法、强度折减法与本文的尖点突变理论计算的边坡安全系数进行对比,如表4所示。由表4可以看出:简化Bishop法、简化Janbu法计算的自然工况下安全系数分别为1.682、1.585,地震工况下安全系数分别为1.204、1.102;强度折减法计算的自然工况下安全系数分别为1.67、1.65,地震工况下安全系数为1.21;本文方法计算的自然、地震工况下安全系数分别为1.65、1.21,与强度折减法、极限平衡法的安全系数相近。计算过程中,因人为主观因素,不能单方面看塑性区是否贯通来确定边坡是否失稳。综上所述,运用尖点突变理论建立的折减系数-位移突变数学模型,实现失稳判定的量化,能较好避免人为因素为判断边坡失稳带来的误差。

表4 不同判别方法下安全系数Tab.4 Safety factors under different discriminant methods

4 结论

1)本文基于尖点突变理论-强度折减法,结合工程算例,建立强度折减系数-尖点突变理论的位移突变数学模型,对自然工况、地震工况进行了分析。结果显示:自然工况下边坡安全系数为1.65,地震工况下安全系数为1.21,因此边坡处于稳定状态。

2)在抗震性能分析计算过程中运用动力强度折减法,充分考虑了动力加载过程中的位移随地震加速度载荷的变化情况,计算的安全系数更加客观准确。

3)结合突变理论,相比于传统的塑性区贯通、计算不收敛、位移突变等失稳判定方法,尖点突变理论位移突变数学模型计算的安全系数实现了失稳判定的量化,并且与强度折减法相比,安全系数基本一致,误差处于可靠范围内,尤其是与极限平衡法的简化Bishop法、简化Janbu法所求安全系数相近,因此证明此方法的可靠性,同时为边坡稳定性失稳判定提供一种新的方法,为类似工程提供理论指导。