一种改进遗传算子的遗传算法组卷策略

张净宇，王 靖，吴志雄，王 旭，丁 宇

（长江大学 计算机科学学院，湖北 荆州 434020）

0 引言

近年来，计算机、人工智能技术在不同领域得到了广泛的应用，与现代教学方式的结合，弥补了传统教学方式的缺陷与不足。在线教学与考核在现代教学方式中的占比不断提升，利用计算机辅助教师出题组卷进行在线考核成为当下研究的热点［1］。与传统试卷命题相比，计算机智能组卷具有以下优点：

（1）智能组卷系统可减轻任课教师在试卷命题的工作量；

（2）有效避免教师在试卷命题上的主观性因素，试卷依据设定的参数自动生成，难度系数和考点范围相对均衡，试卷的实际效用得到提升。

目前，考试组卷大多是从试题库中抽取相应题型的试题进行组卷，通常有以下3 种形式：

（1）人工手动抽取试题；

（2）系统随机完成试题组合；

（3）采用智能组卷策略［2］。

人工选取试题组卷允许任课教师根据教学实际情况进行针对性的训练测试。但这种方式一般需要教师耗时数天来完成试卷命题，且难以满足不同教学大纲要求。

系统随机组合试题常用的方法有随机抽取法和回溯试探法。随机抽取法是从题库中选取出符合条件的试题进行组合，简单、易于实现且抽取速度快，多用于小型的在线考试系统，但组卷过程随机性较大，成功率较低，试卷质量非可控因素较多；回溯试探法则是基于随机抽取法的一种改进方式，该算法记录每次随机抽取的结果，若组卷不成功则返回上一步另行试探，直至组卷成功［3］。回溯试探法的成功率高于随机抽取方式，但时间和空间复杂度较高且生成的试卷质量难以有效保证。

使用智能组卷策略的命题系统普遍采用的是遗传算法。遗传算法的性能主要与算法中设定的选择算子、交叉算子和变异算子有关。选择算子决定了种群进化的方向；交叉算子与变异算子则影响着种群进化的速度。利用传统遗传算法组卷，若选择算子设置不当可能会致使种群收敛到局部最优处或算法难以收敛到最优点，形成“早熟”问题，在组卷实际应用中表现为生成的试卷不能满足用户要求。

为解决传统遗传算法早熟的问题，提高遗传算法在组卷应用中的性能，本文以《C 语言程序设计》组卷为例，提出了一种改进遗传算子的遗传算法组卷策略：种群初始化阶段摒弃了传统遗传算法的二进制编码方式，改用十进制实数对试题编码以降低交叉变异的计算难度；改进的选择算子摒弃轮盘赌算法，采用了轮盘赌与最优个体保存策略结合的综合选择方法以保留优良基因型；改进的交叉、变异算子摒弃传统遗传算法初始设定的固定概率，根据种群进化过程中的适应度值自适应动态调整交叉与变异概率，以控制种群进化的速度。将改进遗传算子的遗传算法与标准遗传算法进行实验比较，结果表明改进遗传算子后的遗传算法不仅组卷速度更快，在最优解和算法的稳定性方面，也呈现出显著优势。

1 组卷问题的数学建模

组卷问题实质上是在多重约束条件下的函数寻优问题，属于典型的CSP（Constraint Satisfaction Problem）问题，同时也属于NP-Hard 问题，要求满足一定前提条件下，在试题库中抽选出合理的试题组合，快速高效地生成一套标准试卷。在解决此类问题过程中，需要设定多个评价指标和一个反映试卷质量的目标函数。设某套试卷题量为m，每道题有n个指标，则此套试卷可视为一个m × n的矩阵。

其中，tij代表本套试卷第i道题的第j个属性。

本文取n为4，分别对应本文建立的组卷数学模型的难度系数、答题时间、区分度和知识点覆盖率的评价指标，试卷评价指标条件定义见表1。

表1 试卷评价指标条件定义Tab.1 Definition of test paper evaluation indicators

在试卷生成中，重点考虑其难度系数、答题时间和区分度与用户设定的期望相近，以满足实际需要，希望生成的试卷知识点覆盖率尽可能的大，以便试卷能综合考察学生对知识点掌握情况。为满足用户需要，根据试卷的4 个评价指标定义给出以下4 项指标的量化评价函数，公式（2）～公式（5）：

其中，D∗、H∗、Q∗分别为用户设定的难度系数、答题用时和区分度，D、H、Q为算法组卷达到的难度系数、答题用时和区分度。

4 个评价函数均经过正向化处理，函数值越大越接近用户期望，反映出该套试卷的试题组合在该指标下表现越好。层次分析法（AHP）是一种定性分析和定量分析相结合的多属性决策方法，广泛应用于评价模型中确定指标权重。由于AHP 法用9个标度表示不同的重要程度，在构建判断矩阵时重要程度划分存在主观因素的影响，判断矩阵的一致性检验问题存在缺陷。而3 标度AHP 法较传统AHP 法引入了判断矩阵的最优传递矩阵，降低了主观性对指标权重的影响。为对比各个指标的相对重要性，确定指标的权重，本文采取了3 标度的AHP对指标赋权，将多目标优化问题转化为单目标的组合优化问题。确定目标函数如式（6）所示：

其中，w为通过改进的AHP 法得到的指标的客观权重。

2 改进遗传算子的遗传算法组卷策略

用户首先设定条件进行约束，在初始随机生成的种群中，若有个体已满足用户设定的条件，则将种群中的最优个体输出，算法结束；否则对其进行选择操作：保存最优的30%个体后整个种群进行轮盘赌选择；被选中的个体依据当前的交叉、选择概率判定是否进行交叉操作和变异操作；将之前保留的30%最优个体替换掉，进行交叉变异后的种群中低于30%最优个体的部分个体，形成新一代种群，即为迭代一次；再检查新种群中的最优个体是否满足用户条件或迭代次数是否达到最大次数。如此重复，直至种群进化完成。

改进遗传算子的遗传算法的流程图如图1所示。

图1 改进遗传算子的遗传算法流程Fig.1 Process of genetic algorithms with improved genetic operators

2.1 初始化种群

首先，对试题（基因）进行编码，通常采用二进制编码方式。但在组卷实践中，发现二进制编码长度随试题量的增加而增加，从而增加了计算难度，一定程度上降低了算法的性能，因此本文采用分段十进制实数编码替代传统二进制编码，生成若干个不重复随机数列，每个实数代表一道试题的题号。为了简化后续交叉与变异的处理，每个数列分为4 小段，分别代表一套标准试卷中的4 种题型：选择题、填空题、运行结果题与程序设计题，将这些数列作为初始种群以供进化。

其次，确定种群的规模，种群规模过小，算法的采样点缺乏会限制算法的表现；种群规模较大，种群基因型丰富，可有效避免算法陷入局部最优，但不可避免地会增加计算量，致使算法收敛速度变慢［4］。一般种群规模设定范围为20～100，本文取值为50。

2.2 选择算子

选择操作用于模拟自然选择的“优胜劣汰”，适应度值高的个体更有机会存活下去，适应度值低的个体则难以遗传至下一代，种群从而逐代进化。常见的选择方法有轮盘赌法与最优个体保存策略，轮盘赌法根据个体适应度值在种群适应度值的比例确定，适应度越高的个体越容易被选中，适应度低的个体也有一定的机率得到遗传，能较好地保持种群基因的多样性，但随机性较大，甚至可能丢弃掉最优个体，造成种群退化。

轮盘赌法中第i个个体被选中存活的概率，公式（7）：

显然，适应度越高越容易被选中。同时，适应度低的个体也有一定的机率得到遗传。

最优个体保存策略是将种群中最优个体直接保存下来，避免经交叉和变异后优良个体的良好基因型被破坏，并用其替换下一代中经交叉变异后适应度值最低的个体，能够保证算法在一定程度上的收敛，但最优个体保存策略也难以排除局部最优解。

为保障遗传算法能够收敛，又能避免过快收敛陷入局部最优。本文改进的选择算子将轮盘赌法与最优个体保存策略结合使用，保存30%适应度最高的最优个体，不参与交叉变异，解集中其余的解则由轮盘赌法选择出来，最后用保存的30%的最优个体替换轮盘赌法选择出来的低于30%的最优个体的部分。

2.3 交叉算子与变异算子

在生物进化的过程中，两个个体间进行交配产生下一代，其实质就是染色体上部分基因进行交换重组，称为交叉运算；产生新一代个体时，个体染色体上可能会发生等位基因的替换，即发生了基因突变。传统的遗传算法采用固定的参数作为交叉概率和变异概率，这种固定的取值方式没有考虑到种群在迭代中的逐步优化，不能动态地适应种群在进化的不同时期的需要。种群迭代早期，个体间相似度较小，为充分进行基因交流，应当提高交叉概率而减小变异概率；随着迭代的进行，种群趋向最优基因型，个体间相似度较高，为避免陷入局部最优，此时应当降低交叉概率而提高变异概率。交叉概率PC影响种群的丰富度，变异概率Pm影响算法解的优劣。Pc越大则种群越丰富，但也越容易破坏优良个体的基因型；Pm越大越容易找到全局最优解，跳出局部最优的陷阱，但Pm过大，算法将退化为随机抽取法。同时，PC与Pm过小时，种群难以产生新个体，进化停滞不前［5］。

鉴于此类问题，有学者提出了一种动态调整交叉与变异概率的自适应遗传算法（Adaptive Genetic Algorithm），其基本思想：对于低于种群平均适应度的劣势个体，为改善该个体适应度，采用较高的交叉概率与变异概率；对于高于种群平均适应度的个体，为保持其优良基因型，应采用较小的交叉概率和变异概率［6］。

公式表达如公式（8）和公式（9）：

其中，k1～k4为控制参数，取值范围（0，1］；fmax是当前种群的最大适应度；favg是当前种群的平均适应度；f为交叉的一组个体中较优个体的适应度或发生变异的个体的适应度。

但这种自适应遗传算法也存在着较明显的缺点：首先，PC与Pm受控制参数k的影响较大，而k的值随机性较强，影响了种群的个体质量；其次，当f ＝fmax时，PC与Pm均为0，即最优个体不再发生交叉和变异，这会导致种群进化停滞不前［7］。

有学者发现logistic 函数在区间两端平滑收敛，趋于固定值，能够较好地描述有界增长的现象，能平衡线性与非线性变化之间的平衡，且logistic 函数的函数值范围从0 到1［8］。

一种简化的logistic 函数如公式（10）：

本文利用logistic 函数的这种良好特性，针对交叉和变异算子进行改进，通过调整系数将其嵌入交叉与变异概率的调节公式中，改进后的自适应交叉与变异概率如公式（11）和公式（12）所示：

其中，α表示种群当前的显示系数，定义为式（13）：

其中，期望EX反映出当前种群的平均适应度，公式（14）；方差DX反应出当前种群适应度的离散程度，公式（15）：

显然，随着迭代次数的增加，种群逐步进化，种群的平均适应度不断提高，趋向于优良基因型，个体间的相似性越来越大，最优解趋于收敛，即离散程度一再降低，相似系数α随之增加［9］。本文确定交叉概率的区间为［0.4，0.9］，变异概率的区间为［0.01，0.1］，因此各控制参数赋值为：k1＝1，k2＝1，k3＝0.4，k4＝0.9，k5＝0.198，k6＝1，k7＝0.001，k8＝0.1。采用自适应调整的交叉与变异概率进行交叉与变异操作，其过程如图2、图3 所示。

图2 交叉操作Fig.2 Crossover operation

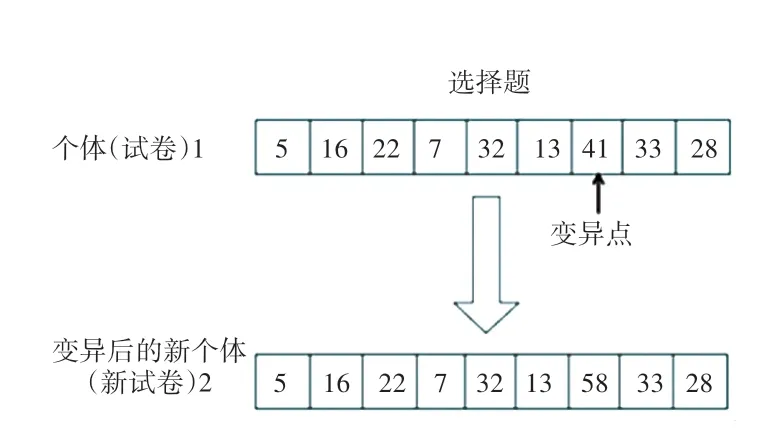
图3 变异操作Fig.3 Mutation operation

3 仿真实验与分析

为验证本文策略在组卷实践中性能上的提升，以《C 语言程序设计》试卷为例，设定用户期望、标准遗传算法参数与系统开发环境，见表2～表4。

表2 设定用户期望Tab.2 Set user expectations

表3 设定标准遗传算法参数Tab.3 Set standard genetic algorithm parameters

表4 系统开发环境Tab.4 System development environment

采用本文改进遗传算子的遗传算法在上述条件下组卷，种群进化过程中适应度的变化如图4 所示。

图4 改进算法适应度变化Fig.4 Improved algorithm adaptability variations

由图4 可知，区别于标准遗传算法采用的轮盘赌选择方式导致进化曲线波折震荡，本文的选择算子采用最优个体保存策略与轮盘赌结合的方式，在种群不断进化的过程中仍能保存优良个体的基因型，使得种群稳健的逐步提升，不会出现震荡“退化”的现象。在迭代至第五代附近，即使没有进化出更优的个体，仍能保持着最优基因型不退化。

按此要求生成的试卷样例展示如图5 所示。

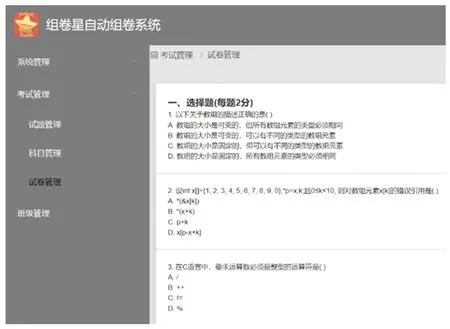
图5 生成试卷展示Fig.5 Generate test paper presentations

将其与同等条件下标准遗传算法生成的试卷进行对比实验，并就实验结果进行分析：

（1）通过30 次的试验，改进遗传算子的遗传算法达到收敛平均需要48 代，而标准遗传算法收敛所需迭代次数约为本文算法的2～3 倍，显然本文算法在计算速度方面优于标准遗传算法，更适宜应用于组卷等实时请求场景；

（2）随着进化次数的增加，本文算法最优个体的适应度值不断提高，逐渐高于标准的遗传算法最优个体适应度值，两种算法对用户不同期望的满足程度如图6 所示，本文算法生成的试卷在总体上更能满足用户的期望要求。

图6 两种算法对用户不同期望的满足程度Fig.6 The degree of satisfaction of the two algorithms to the different expectations of users

4 结束语

智能组卷策略是计算机辅助教学研究的热点问题，需综合考虑试卷难度、考试时长、区分度系数以及知识点覆盖等多种约束条件。本文将改进的遗传算子融于标准遗传算法中，又基于组卷问题的实际需求，调整了编码方式、加入了允许误差，提出了一种多约束条件下的智能组卷策略。在以《C 语言程序设计》为例的试卷命题仿真对比实验中，验证了本文的组卷算法相较于传统遗传算法具有更高的应用价值。