培养小学生数学建模能力的策略研究

郑国良

几何直观是研究数学的重要思想方法，而数学建模是一种通过抽象、简化建立能近似刻画并“解决”实际问题的、有效的数学手段。它有助于学习者多渠道获取知识，培养抽象思维、立体思维和空间想象力，形成良好的学习习惯和学习策略。

一、问题的提出

数学建模在实际教学应用中往往存在以下问题：

（一）教师对建模价值认识淡薄

很多数学教师在进行教学设计时，教学思路局限在“知识与技能”维度上，单纯地为学生获取数学知识而设计，从铺垫到新课再到练习，没有借助生活情境作为支撑和背景。虽然教学设计中也有一些过程设计，但其过程设计更多体现在数学学科内部知识的演化，忽略了数学建模意识和建模思想。

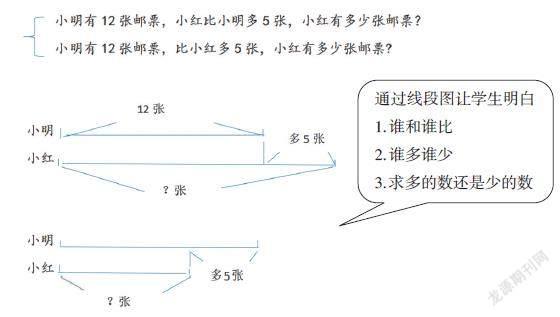
例如：在低段解決“比多比少”的问题时，学生出示问题：“小明有12张邮票，比小红多5张，小红有多少张邮票？”然而，出现正确率很低的现象，是因为学生将其与“小明有12张邮票，小红比小明多5张，小红有多少张邮票”这一数量关系混淆了，教师在解决“比多比少”问题时潜意识地让学生形成看到“多”用“加”，看到“少”用“减”的捷径方法。这样的解题方法抛弃了建模的过程，主观上抹杀了学生正确分析数量关系的过程。

（二）学生应用模型意识差

学生的学习探究、合作拘泥于形式，缺少必要的数学模型意识和应用模型意识，很少将数学学习方式与建模联系起来，仅仅是单纯的数学技能的训练，没有“建模”和“用模”的痕迹。

例如：在教学乘法分配律时教师讲解得很生动，可是学生一碰到简便计算时易错误百出，最常见的是与“乘法结合律”相混淆。其主要原因是：第一，学生对乘法分配律的理解只停留在运算概念的表象中，没有归入自己的认知结构；第二，对乘法分配律缺乏直观体验。

（三）测试评价内容单一

教学日常测试卷更多时候是局限于应用规律和公式来解决生活问题，是对学生知识技能的掌握考评，是以知识的深度作为“难题”来衡量数学是否学好的标准。而对培养学生建模意识、检测学生建模能力为目的的数学问题的解决是少之又少，这样的评价内容和手段是有偏颇的，这样的试题对日常教学以及教师观念的转变有很强的导向作用。

二、研究的过程和方法

培养学生的几何直观能力是小学数学教学的重要目标，它在帮助学生理解数学知识、培养思维能力、建立模型思想等方面都有重要的作用，教师应在教学中使学生借助几何直观经历建立数学模型、应用数学模型解决实际问题，积累一定的数学活动经验，让学生真正体会到数学是“讲道理”的学科，而不是靠“背公式”“记方法”就能学好的学科。

（一）借“线”建模，形成体系

1.关注数轴，发展数感。数轴不仅将抽象的“数”直观形象化，而且有助于理解不同的数、数的运算，数轴在一二年级频繁出现，然后贯穿小学六年。

例如：在一年级中为了让学生建立数序、数的大小的表象，就借助“数轴”填数这个几何直观的模型，帮助学生形成数的大小表象，比较出数字与数字之间的距离。

数轴在理解正数、负数的意义，大小、相差大小等方面也是发挥着至关重要的作用。数轴以0为分界线，0的左边是负数，比0小，0的右边是正数，比0大。如果要比较两个正数与负数之间相差多少在数轴上数一数就一目了然了，简单、直观地让学生发展了数感。

“数轴”模型在小学阶段不断出现，主要是让学生认识到几何直观模型的重要性，不断积累几何直观的经验。

2.利用线段图，破除难点。线段图在解决数学问题中起到了关键性的作用，学生通过绘制线段图，可以理清数量关系，抓住本质所在，真正建立解决此类问题的模型。在小学阶段中解决“比多比少”的数学问题是以后学习分数、百分数中相关应用题的基础，所以必须在低段就要引导学生通过画线段图来理解数学问题。例如：

借助线段图，在不断地绘制中真正理解此类应用题的数量关系，在脑海中建立解决此类数学问题方法的模型。

（二）借“图”建模，呈现过程

1.绘制“示意图”，深层建构算理。在代数领域，学生掌握了计算方法，但对算理的理解经常停留在“知其然而不知其所以然”，数学教学中很多代数问题可以转化成直观图形来思考，形象直观地描述常常会有很好的效果，能帮助学生对知识进行深层建构，加深对算理的理解。

例如：在教学  +  +  +  =？，由于数字不大，很多学生会选择先进行通分，化成同分母分数后再直接相加，如果让学生用简便方法计算，学生就不知道方法了，为了让学生能更清楚明白算理，教学时采用画示意图，在图中学生能清楚看到4个分数相加的和就是阴影部分总和，因为空白部分是  ，所以阴影部分的和就是  。

2.绘制“过程图”，丰富建构过程。“过程图”其实就是“思维导图”。数学的本质是要让学生的思维在比较中逐步走向深刻，经历抽象数学问题、构建数学模型的过程，更重要的是渗透在学习过程中的诸如列表、画图等的思维导图让学生的模型思想进行有效建构。

例如：在教学《沏茶问题》时，教材凸显了课程标准中要求让学生通过“经历”和“体验”数学思想和模型建构的形成过程，以学生能在家做点家务的生活经验为基础，通过绘制思维导图来感受工作的有序、合理安排。

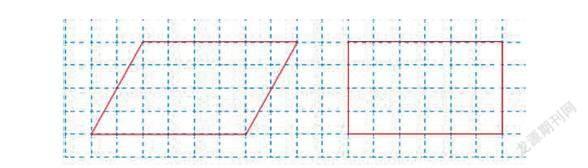
3.利用“方格图”，建构空间模型。在平面图形教学中，如果用好“方格图”就可以有效地促进学生空间观念的建立。在平行四边形、三角形、梯形的面积计算公式的推导，一般先出现方格图，让学生用数方格的方法计算面积，然后通过引导学生观察它们的底和高的数据与面积之间的关系，借助方格图探究未知图形与已知图形面积关系的本质，建构面积计算的模型。

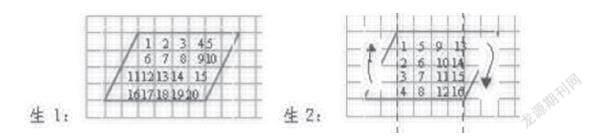
在教学《平行四边形面积》，教师让学生在方格图中数一数一共有多少格，面积是多少？（每一个小格是1平方米，不满1格按半格算）

学生通过数、割、移、补等方法数出平行四边形面积。

在转化过程中，教师刚好可以顺势引导平行四边形的底和高与长方形长和宽的关系，由此得出平行四边形面积计算方法也是水到渠成。学生经历探究过程，计算方法模型也就在学生脑海中深深地打上了烙印。

三、结束语

基于几何直观培养学生建模的能力，既是过程，又是结果，具有动态性、模型性的特点。利用几何直观能让学生将直观的图形语言和抽象的数学语言有机地结合起来，使形象思维和抽象思维结合起来，为学生数学建模的学习开辟了一个重要的途径。对于怎样探索小学数学建模教学的方法与途径，找寻适合教材中不同学段、不同阶段的数学模型，构建数学建模的基本方式，要以具体的课例研究为载体，从各种课例研究实践中，提炼出共性的做法，构建出教学模式，这才是我们需要共同努力的方向。

（徐德明）