孔系自参考位置度最小区域的一般化判别方法
秦玲 唐哲敏 程彬彬

摘 要:评定孔系自参考位置度時,没有一般化的判别方法来裁定某个算法构造或找到的误差边界是否满足最小区域条件。针对这一问题,研究基于边界点的孔系自参考位置度最小区域一般化判别方法。分析了孔系的测点集与误差边界的相对空间关系,建立了孔系位置度最小区域模型;分析了最小区域判别逻辑的基本数理形式及其基本推论;建立边界点的基本运动矩阵,并将最小区域的判别逻辑问题转化为等效的基于矩阵的一般化判别方法。最后通过一个实例验证了提出的孔系自参考位置度最小区域一般化判别方法。
关键词:判别方法 位置度 孔系 自参考 误差评定
中图分类号:TH161 文献标识码:A
A Generalized Discrimination Method for the Minimum Zone of Self-Reference Positional Tolerance of the Pattern of Holes
QIN Ling1 TANG Zhemin2* CHENG Binbin1
(1. Guilin Institute of Information Technology, Guilin, Guangxi Zhuang Autonomous Region, 541004 China;
2. Guilin University of Electronic Technology, Guilin, Guangxi Zhuang Autonomous Region, 541004 China)
Abstract: When evaluating the self-reference positional tolerance of the pattern of holes, there is no generalized discrimination method to determine whether an algorithm construction or found error boundary meets the condition of the minimum zone or not. In view of this problem, a generalized discrimination method for the minimum zone of the self-reference positional tolerance of the pattern of holes based on boundary points is studied. This paper analyzes the relative spatial relationship between the measure point set and the error boundary of the pattern of holes, establishes the model of the minimum zone of the positional tolerance of the pattern of holes, analyzes the basic mathematical form and its basic inference of the discriminant logic of the minimum zone, establishes the basic motion matrix of boundary points, transforms the discriminant logic problem of the minimum zone into an equivalent matrix-based generalized discrimination method, and finally uses an example to verify the proposed generalized discrimination method for the minimum zone of the self-reference positional tolerance of the pattern of holes.
Key Words:Discrimination method; Positional tolerance; Pattern of holes; Self-reference; Error evaluation
孔系自參考位置度误差是机械零部件的一项重要几何误差,通常用于保障以孔系安装定位的零件的可装配性及装配精度,在相关标准中的严格评定方法是最小区域法[1-2]。几何误差最小区域的几何判别条件比较复杂,国标和ISO给出了给定方向上的两条平行直线、两个平行平面及圆柱的共计十余条几何判别准则,但并未列举孔系位置度误差的最小区域判别准则。
为了减少形状误差的判别条件款项,丁喜波等和熊有伦从不同角度提出了基于几何学的统一判别方法[3-5],统一了各类形状误差的判别,但具体操作和计算仍较复杂,因此,目前几何误差的最小区域判别方法大多与具体评定算法相关。Ameta G、肖欢等利用T-MAP等方法构造的变动域凸包,可以借助计算几何方法枚举所有“顶点”的误差区域并找出其中最小值,即判别方法为数值上的“区域最小”[6-7],这类方法能准确判定最小区域,但不适合测点较多的情况。自适应虚拟量规法、旋转投影法等基于被测要素的几何特性来构造边界并搜索大小更合适的包容边界,直至满足最小区域的几何判别条件[8-9]。闵浩晨、李新、LUO J、王生怀等分别利用牛顿法、二分法等传统优化方法和差分进化算法、混合教与学算法等智能优化算法进行几何误差评定,这些优化算法的判别方法通常为两次迭代间步长或函数值的变化较小[10-13];当出现争议时,这类方法仍需要采用几何判别方法裁定。
综上所述,在经常需要处理大量测点数据的当下,还缺乏一种一般化的、程式化的最小区域判别方法,以便在出现评定争议时裁定算法是否找到了最小区域。本团队近期研究了若干类型几何误差最小区域的一般化判别方法,通过分析边界点与误差区域之间的相对空间关系,建立边界点的基本分析矩阵,尝试解决了圆柱度、空间直线度误差的一般化判别方法[14-15]。
孔系位置度误差是机械零部件中典型、重要且比较复杂几何误差,为解决其最小区域判别问题,本文研究其基于边界点矩阵的一般化的、程式化的判别方法。分析了圆柱测点集与最小区域边界之间的空间关系以及最小区域成立条件的数理逻辑形式,并利用边界点集矩阵的性质提出一种最小区域的一般化判别方法。最后,通过一个评定实例验证了提出的孔系位置度一般化判别方法。
1 孔系位置度包容区域模型
1.1 孔系测点集与包容区域的相对方位
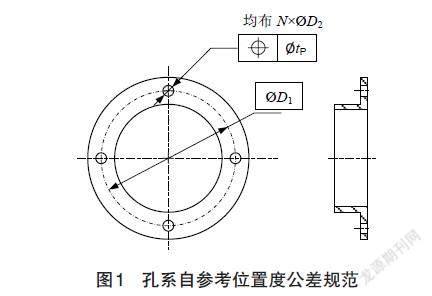
孔系位置度误差包容区域是保持理想方向、位置的若干直径相同的圆(柱),且每个圆(柱)都包容着相应的孔心;孔系位置度误差值为构造的最小圆(柱)的大小。如图1所示,当孔系中各孔的位置不由其它几何要素定义时,各孔位置的参考关系完全由自身决定,这时,孔系位置度是自参考的位置度。孔系自参考位置度通常用于保障以孔系安装定位的零部件的可装配性及装配精度。
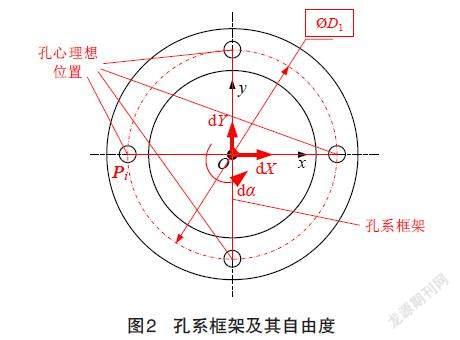
如图2所示,构造孔系自参考位置度包容区域时,可以先建立XOY平面坐标系,在坐标系上建立评定孔系位置度的孔系框架。对于孔系自参考位置度而言,孔系框架的几何形状是固定的,但方向、位置没有外部参考物,因此,孔系框架是可以浮动的,具有在XOY平面内的两个平移自由度dX、dY和绕原点的转动dα。理想孔心可以描述为被测孔心Pi的集合{Pi|Pi=(Xi,Yi),i=1,2,…}。
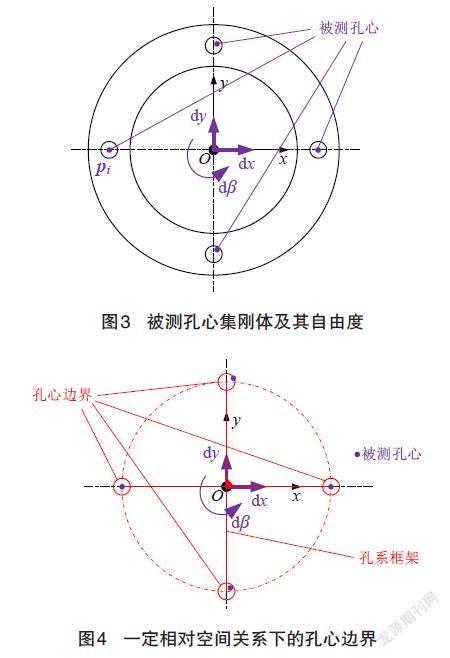
如图3所示,作为零部件的组成部分,各被测孔心可以视为刚体上的若干固定点,它们之间的相对位置是固定的;因为自参考位置度公差规范没有直接定义测点与参考系之间的关系,所以被测孔心集刚体{pi|pi=(xi,yi),i=1,2,…}也可以相对于XOY平面、相对于孔系框架浮动,被测孔心集刚体{pi}自由度方向为沿x、y轴的平动dx、dy和绕原点的转动dβ。
如图4所示,孔系框架、被测孔心集刚体都是可以浮动的,当它们处于某个相对空间关系时,可以根据各被测孔心到孔系框架上相应理想点的距离的最大值,作出相应的孔心边界。一定空间相对关系下,测点pi到孔系框架上相应理想点Pi的距离为ri=|Pi-pi|,孔心边界的半径D=2max ri。
孔系自参考位置度的值应当为孔系框架和被测孔心集刚体浮动过程中孔心边界直径的最小值Dmin。显然,取决于孔系框架和被测孔心集刚体之间的相对空间位置,两者只需要保持一个运动、一个静止即可。为便于分析计算,本文令孔系框架保持静止,令被测孔心集刚体运动。
当按自由度方向调整被测孔心集刚体时,被测孔心pi的方位变化趋势dpi如公式(1)和图3所示。
其中:Rdβ为测点绕原点O逆时针旋转的坐标变换矩阵,E2×2为单位矩阵;自由度调整量极小,因此sin dβ≈dβ,cos dβ≈1,dβ·dβ≈0。
1.2 孔心边界的变化趋势
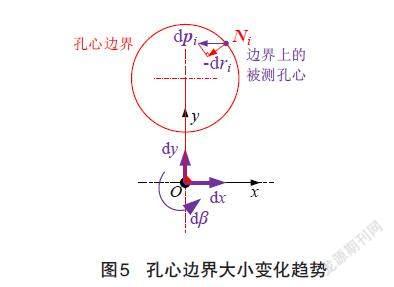
孔系框架和被测孔心集刚体有相对方位变化趋势时,孔心边界的大小变化趋势仅受与孔心边界接触的被测孔心影响。如图5所示,被测孔心pi到理想孔心Pi距离的变化趋势dri,是dpi在孔心边界法向Ni=[(Xi-xi)/ri,(Yi-yi)/ri]T上的投影,即dri=-dpi·Ni。将dpi表达式公式(1)代入投影公式,可以得到dri的代数表达式,如公式(2)所示:
为便于分析,可以将公式(2)中pi自由度运动趋势合记为运动趋势向量Ψ=[dx,dy,dβ]T,Ψ的系数合记为运动系数向量Ai,如公式(3)所示。
将Ai、Ψ代入公式(2),可以得到dri的线性向量表达式,如公式(4)所示。
记G={g}为与孔心边界接触的被测孔心序号集,则孔心边界变化趋势dR=min drg。代入公式(4),可以得到dR的向量表达式,如公式(5)所示。
2 孔系自参考位置度最小区域的表达
2.1 2 孔系自参考位置度最小区域的逻辑形式
孔系自参考位置度的最小区域可以一般性地描述为:被测孔心刚体与孔系框架间的相对方位已调整至最佳,相对方位发生任意改变时,在孔心边界上至少存在一个被测孔心使孔心边界不会更小。据此可以建立最小区域判别的基本逻辑形式,如公式(6)所示,其中,h∈G。
公式(6)是对于运动趋势向量Ψ的“求证”形式,不便于直接分析其是否成立。其互斥的否命题形式如公式(7)所示,是对于运动趋势向量Ψ的“求解”形式,有利于进行下一步数学分析。因此,本文建立基于公式(7)的最小区域判别:如果公式(7)成立,则孔心边界不是最小区域,否则,孔心边界是最小区域。
记A=[…,AgT,…]T为孔心边界上被测孔心集的运动系数矩阵,b=[…,drg,…]T为运动常数项,则公式(7)等价于公式(8)。
2.2 基于逻辑表达式的一般化判别方法
设孔心边界上被测孔心数目为m,rank(A)=r,则Ag共有m个,A共有m行。当rank([A,b])=rank(A)=r时,AΨ=b总是有解,即,公式(8)总是成立,孔心边界不是最小区域。下面讨论rank([A,b])>r时公式(8)的成立条件。
记B=[…,b,…]T,则公式(7)中的不等式组{AgΨ<b}在任意给定超平面AΨ=B上的基本解集Fj={Ψ}j不超过Cmr个,相关定义如下:
定义1:在AΨ=B中任选r个线性无关的运动系数向量Ag、对应的drg及常数项b,分别集合成矩阵Ar、常数项br及常数项Br;线性方程组ArΨ=Br的解集Fj={Ψ}j就是不等式组{Au,vΨ<b}在超平面AΨ=B上的一个基本解集;其余的运动系数向量Ag及对应的drg分别集合成矩阵As和常数项bs,s∪r=G。
由公式(11)可知,可以先求解方程ArΨ=Br的一个解Ψ,然后考察Ψ是否满足P2(Ψ),即可判断相应的基本解集Fj={Ψ}是否为有效基本解集。
如果Ψ满足P2(Ψ),则公式(8)成立,即公式(7)成立,孔心边界并非最小区域;如果Cmr个ArΨ=Br的特解Ψ都不满足P2(Ψ),则Cmr个ArΨ=Br的任意解Ψ都不满足P2(Ψ),则公式(8)恒不成立,即公式(7)不成立而公式(6)成立,孔心边界是最小区域。
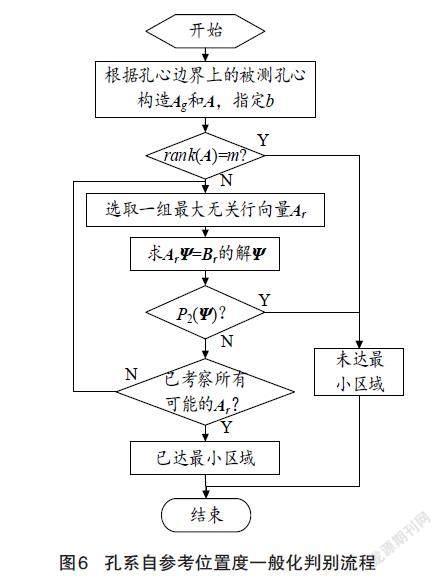
综上所述,孔系自参考位置度的最小区域统一判别方法的基本流程如图6所示。
3 实例验证
本节以仿真法兰盘的一组测点数据为对象,用优化法评定仿真孔系的自参考位置度,并用本文提出的方法辨别优化法是否准确构建了自参考位置度的最小区域,以验证提出的判定方法。
3.1 仿真法兰盘的自参考位置度评定
本例根据法兰盘孔系公差规范(图7)用Matlab对法兰盘孔系进行仿真,每个孔16个仿真点,如图8所示;测点原始数据可以通过编辑部或作者免费咨询获取。
拟合得到8个孔的仿真中心pi后,可以用优化法求解孔系自参考位置度,如公式(12)所示;优化求解方法为Matlab R2021a自带的fminucon函数。
在MATLAB R2014a中,自编程序求解得到仿真法兰盘的自参考位置度为0.045mm,构成与最小区域边界接触的仿真孔心的序号为1、3、5、6,如表1所示。
3.2 评定结果的判别
基于提出的判別方法,对表1中的评定结果进行判别,判断优化法是否满足最小区域条件。将位于孔心边界上的仿真孔心的最终位置代入公式(3),可以求出运动系数向量Ai及运动系数矩阵A,如公式(14)所示。
指定m=4个b=-1,并将其集合为b=[b,b,b,b]T=[-1,-1,-1,-1]T。因为rank([A,b])=4>rank(A)=3,所以需要选取不超过Cmr=C43=4个Ar并检验基本解的有效性。本例借助MATLAB 2014R内置函数“nchoosek”在A的4个行向量中选取3个行向量。
以第一组为例,选取A的前3行为Ar,并将第4行向量视为As;选取Br=[b,b,b]T=[-1,-1,-1]T。用Matlab 2014R内置函数“\”求得ArΨ=Br的解Ψ。因为A4Ψ=-0.0993>-1,P2(Ψ)不成立,所以基本解集(单元素集)F1=Ψ*并不是有效基本解集。
依次检验4组Ar对应的基本解集,发现并不存在有效基本解集。因此,优化法求得的位置度孔心边界满足最小区域条件,孔系的自参考位置度误差为0.045mm。
4 结语
分析了孔系被测孔心集刚体与孔心框架之间的相对空间关系;基于数理逻辑、线性方程组和不等式组理论,分析了孔系自参考位置度误差的最小区域的判别条件,并给出了相关线性矩阵及流程图。提出的判别方法由程式化的运算、条件选择构成,是一种程式化的、一般化的代数判别方法,可以在出现评定争议时裁定算法是否找到了最小区域。
用优化法评定了一个仿真法兰盘的孔系自参考位置度误差,用提出的方法检验了优化法的评定结果。提出的判别方法识别了优化法求得的最小区域,具备最小区域判别的能力。
该文推导了孔系自参考位置度误差最小区域的一般化判别方法,其中运用的自由度、法向量、数理逻辑、线性理论等也适合其他形状的最小区域评定。未来可以参考该文方法继续研究轮廓度等形状、方向和位置误差的最小区域判定。
参考文献
- AMETA G,SINGH G,DAVIDSON JK, et al.Application of T-MAPS for Composite Position Tolerance for Patterns of Features[C].ASME International Design Engineering Technical Conferences/Computers and Information in Engineering Conference(IDETC/CIE 2017),2017,1:V001T02A014.

