基于双参数自适应优化的无人履带车辆轨迹跟踪控制

卢佳兴, 刘海鸥, 关海杰, 李德润, 陈慧岩, 刘龙龙

(北京理工大学 机械与车辆学院, 北京 100081)

0 引言

近年来,地面无人平台在港口运输、疫情防控、野外搜救以及战场环境中得到了越来越多的应用,轨迹跟踪控制作为无人驾驶的关键技术,其发展也得到了越来越多学者的关注,其中以模型预测的控制算法应用较多[1-4]。然而,目前大多数都是基于定参数的轨迹跟踪控制算法,很难保证车辆在复杂多变工况下的跟踪精度和稳定性。基于此,有学者提出自适应参数调整算法,包括更精确的车辆模型参数在线估计、更合理的控制系统结构设计以及更高效的优化算法架构设计等。Zhao等[5]结合瞬时转向中心模型提出履带车辆滑动参数实时估计算法,对越野工况下的履带车辆轨迹跟踪进行了探究。但由于越野工况下地面-履带的相互作用关系难以精确表征,因此基于车辆模型参数在线估计的方法很难为系统提供稳定、可靠的输入,且在线估计对系统的实时资源配置要求较高。Pereida等[6]提出了将模型预测控制(MPC)与底层控制器相结合的框架。Yuan等[7]基于模糊推理、预瞄模型、预瞄点搜索算法建立了自适应轨迹跟踪控制系统,提升了不同速度下轨迹跟踪的工况适应性。李睿等[8]基于自动驾驶履带车辆的运动学与动力学耦合模型,采用自适应控制方法对模型进行前馈补偿。Wang等[9]基于多层感知机(MLP)神经网络和贝叶斯优化相结合的算法,提升了控制性能。这些研究成果证明了以MPC为基本框架,通过增加前馈、数据学习等方式提升轨迹跟踪性能的有效性,但是缺乏在实际高速履带平台的验证。

模型预测轨迹跟踪算法中,影响控制效果的控制参数主要包括代价函数中的各权重系数、控制时域中的相关参数等,其中控制时域长度和控制时间步长影响较大[7,10]。基于学习的控制参数自适应轨迹跟踪算法的主要建模过程包括最优参数组合评价与提取、在线最优控制参数预测两部分。在最优参数提取方面,可变惯性权重的改进粒子群优化(PSO)算法已被学者广泛应用。赵新等[11]基于改进PSO算法建立引信与战斗部配合威力计算模型,实现了更高精度的最大杀伤面积计算和更快的收敛速度。谭顿等[12]将改进PSO算法用于寻找同步控制系统的最优PID系数,有效减小了系统超调与同步控制误差,提升了系统响应速度。在线最优参数预测方面,常用的算法有高斯混合回归、支持向量机[13]、分类与回归决策树[14]、神经网络[15]等。其中,基于神经网络的算法应用较广。牛江川等[16]利用盾构施工案例的大量历史数据作为样本数据,基于PSO-反向传播(BP)神经网络进行模型训练,实现盾构刀具配置方案的合理推荐,在计算精度和训练时间上实现了较大的提升。但未见在无人履带车辆方面的研究成果。

本文基于改进PSO-MLP算法,以控制时域长度tl和控制时间步长ts为优化目标,以离线和在线相结合的方式,设计一种双参数自适应优化的无人履带车辆轨迹跟踪控制算法,总体框架如图1所示。离线部分,首先对不同控制参数下的履带车辆轨迹跟踪响应状态信息进行提取,得到包含运动基元类型、参考轨迹Sr、轨迹跟踪响应信息、车辆状态ξ(k)以及控制参数的车辆历史数据集合DH;然后,基于改进PSO算法得到不同运动基元下的最优控制参数组合,并构建训练数据集,利用学习率自适应优化算法完成对MLP神经网络模型的训练。在线部分,首先对运动基元类型和车辆状态进行特征匹配,基于MLP神经网络对控制时间步长ts和控制时域长度tl进行预测,为轨迹跟踪控制模块提供自适应双参数输入。然后,结合自适应参数输入、车辆模型、约束条件C以及代价函数等建立轨迹跟踪控制器,得到最优控制量u,实现双侧独立电驱动履带平台的自适应轨迹跟踪控制。

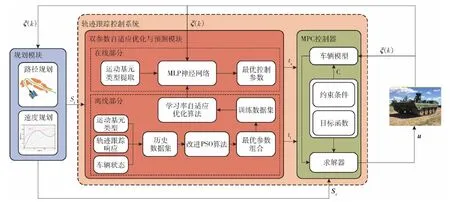
图1 总体框架Fig.1 Overall framework

1 履带车辆模型

本文基于履带车辆运动学模型生成MPC控制器的状态空间。同时,为弥补车辆运动学模型往往忽略车辆动力学特性的缺陷,引入履带车辆动力学模型,为运动学模型提供安全边界。

1.1 履带车辆运动学模型

本文的研究对象为双侧独立电驱动履带车辆,根据履带车辆的差速转向特性,为了与规划模块生成的参考轨迹的坐标方向保持统一,建立图2所示的履带车辆运动学模型。

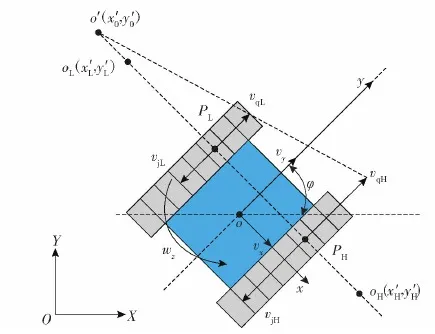
图2 履带车辆运动学模型Fig.2 Kinematics model of a tracked vehicle

图2中:OXY为固连于地面的惯性坐标系,坐标轴OX、OY所在平面与路面重合;oxy为固连于履带车辆并随履带车辆共同运动的牵连坐标系,o(x0,y0)位于履带车辆的几何中心,ox为车辆的横向方向,oy为车辆的纵向方向,且ox、oy所在平面与路面平行;vx、vy分别为车辆的横向速度、纵向速度,ωz为车辆的横摆角速度,定义逆时针为正,φ为车辆的航向角;o′(x′0,y′0)为惯性坐标系中履带车辆的瞬时转向中心,oL(x′L,y′L)、oH(x′H,y′H)分别为低速侧履带、高速侧履带接地面的瞬时转向中心(转向极),三者中心在一条垂直于车辆纵向对称面的直线上;vqL、vqH分别为低速侧和高速侧履带上PL、PH点的牵连速度;vjL、vjH分别为低速侧和高速侧履带的卷绕速度。

履带车辆通过调整两侧履带的速差实现转向操控,在固连于地面的空间笛卡尔坐标系下,车辆的状态向量可以表示为ξ(x0,y0,φ),由车辆位置坐标和车辆航向角组成,则履带车辆的运动学模型可以描述为

(1)

基于传统的运动学模型,当履带的卷绕速度为0 m/s时,无法通过表达式反求出履带的卷绕速度,基于瞬时转向中心的运动学模型可以很好地解决这个问题[17]。根据图2中建立的履带车辆运动学模型坐标系体系,结合文献[17]中的模型建立过程,推导得到如式(2)所示的基于瞬时转向中心的履带车辆运动学微分方程:

(2)

1.2 履带车辆动力学模型

履带车辆特殊的驱动方式,导致履带和地面的相互作用关系的复杂性,为简化建模,进行如下所示的假设[18]:

1)车辆在转向过程中,不考虑履带的沉陷作用和推土作用;

2)履带载荷沿着履带长度方向均匀分布;

3)在进行阻力分析时,忽略空气阻力的作用;

4)在转向过程中的行驶阻力系数与直驶过程相同。

图3所示为履带车辆的动力学模型。图3中:C为车辆的重心;P为牵连坐标系中车体转向中心;L为履带接地段长度;B为履带中心距;xC、yC分别为履带车辆的重心与几何中心的横向、纵向距离;λC为由离心力作用产生的转向中心纵向偏移量;R′为履带车辆的稳态转向半径;R为惯性坐标系中履带车辆的瞬时转向中心与车辆重心的垂直距离;FC为车辆转向时产生的离心力;FCx、FCy分别为离心力的横向分量、纵向分量;FrL、FrH分别为低速侧、高速侧履带接地段所受的地面变形阻力;FyL、FyH分别为低速侧履带制动力、高速侧履带驱动力;FxL、FxH分别为低速侧、高速侧履带所受横向阻力的合力;MμL、MμH分别为低速侧、高速侧履带所受的转向阻力矩,μ表示转向阻力系数。

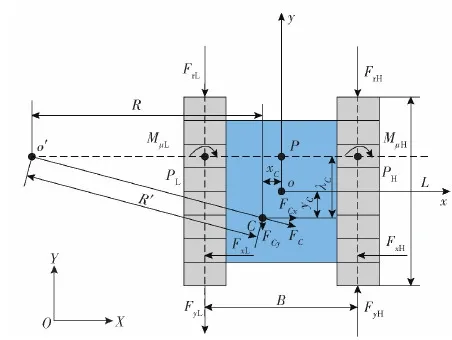
图3 履带车辆动力学模型Fig.3 Dynamic model of a tracked vehicle

基于达朗贝尔原理,在oxy坐标系中对车辆几何中心建立履带车辆动力学方程组:

(3)

式中:m为履带车辆的整车质量;δ为履带车辆旋转质量换算系数;Mμ为转向阻力矩,Mμ=MμL+MμH;J为履带车辆绕z′轴的转动惯量。

考虑履带车辆在转弯时,由于离心力作用导致的车辆转向中心前移、载荷转移,根据履带车辆动力学方程组式(3),将FyL、FyH、λC作为未知量,车辆在进行平地转向时为匀速转向,在已知规划路径曲率特征、纵向规划速度以及车辆的结构参数、性能参数等的情况下,对上述的3个未知量进行求解,可得

(4)

2 基于模型预测的轨迹跟踪控制器

MPC模块根据规划模块提供的参考路径曲率特征以及参考速度、车辆状态信息,结合双参数自适应优化与预测模块输出的控制时域长度、时间步长,考虑车辆运动学边界和电机外特性,进行最优控制序列的迭代求解,并将第1个时域内的控制量下发给执行器,实现最优控制。

2.1 目标函数

在进行轨迹跟踪控制器的设计时,系统可以表达为

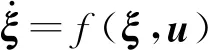
(5)

式中:u=[vjL,vjH]。由式(2)可知,要实现对车辆状态的准确预测,还需要得到车辆瞬时中心的位置,该参数通过状态观测模块提供给MPC控制器,在此不作赘述。

对式(5)中的连续系统模型进行离散化,可得

(6)

式中:ξ(k)、u(k)分别为k时刻的车辆状态向量、控制输入向量,k≥0;yc(k)为k时刻的控制输出向量;yb(k)为k时刻约束输出向量。控制量、控制量增量Δu(k)约束以及输出约束分别为

(7)

式中:umin、umax分别为控制量下限值、上限值;Δumin、Δumax分别为控制量变化率的下限值、上限值;ymin(k+j)、ymax(k+j)分别为k+j时刻约束输出的下限值、上限值。

在进行代价函数的构建时,需要综合轨迹的跟踪精度、稳定性。在k时刻,基于离散非线性模型的MPC优化问题可以描述为

(8)

(9)

式中:J(ξ(k),Uk)为目标函数

(10)

le、he、v分别为轨迹跟踪的横向偏差、航向偏差、实际车速,ldesired、hdesired、vdesired分别为期望横向偏差、期望航向偏差以及期望车速,Q、R、P、M、N分别为对应项的权重系数矩阵;Np、Nc分别为预测时域、控制时域的个数,且Nc≤Np。

2.2 约束设置

为保证履带车辆不发生侧翻,车速需要满足:

(11)

式中:kr为侧翻阈值系数;β为车辆的侧倾角度;hg为车辆重心高度。

为了保证车辆在转弯时不发生失控的情况,车辆的转向中心纵向偏移量需要满足:

(12)

整理得:

(13)

式中:ks为侧滑阈值系数;fφ为路面附着系数;α车辆俯仰角度。

在规划轨迹已知的条件下,在入弯之前对车辆转向的转矩需求进行预测:

(14)

(15)

T(vy,ρ)=max [TL,TH]

(16)

式中:TL、TH分别为低速侧、高速侧履带转矩需求;η为机械传动效率;i为综合传动比;r为驱动轮半径;T为基于规划轨迹的电机最大转矩需求;ρ为路径的曲率。

电机外特性是影响电机性能的边界条件,图4为本文履带平台的电机外特性。在基于转速控制的轨迹跟踪研究中,如果在当前电机转速下,实际车辆行驶的转矩需求达到或接近电机外特性曲线上的转矩极限值,车辆的转矩调节范围就会受到约束,在当前转速下的转向能力就会得到制约,难以满足车辆轨迹跟踪控制的性能要求,严重时甚至会导致轨迹不可控。

图4 电机外特性Fig.4 External characteristics of the motor

将电机的转矩和功率作为约束输出,并设置转矩保护系数kT和后备功率保护系数kP,可得

T(vy,ρ)kT≤Tmax(vy)

(17)

P(vy,T)kP≤Pmax(vy)

(18)

式中:Tmax(vy)、Pmax(vy)分别为当前电机转速下电机可以提供的最大转矩和最大功率;P(vy,T)为当前工况下电机功率的需求。

3 双参数自适应优化与预测模块

双参数自适应优化和预测模块基于运动基元类型进行车辆历史数据的提取,历史数据集基于实验室现有的双侧独立电驱动无人履带平台,以机器人操作系统(ROS)作为通信系统完成对越野工况下车辆状态信息的记录和储存[4]。通过离线优化和在线预测,为MPC控制器提供自适应最优控制参数输入。

3.1 算法总体介绍

模块以履带车辆历史数据集合为输入,主要基于改进PSO-MLP算法,完成最优参数组合的离线提取和最优控制参数的在线预测。基于上述算法得到了运动基元类型与轨迹跟踪最优控制参数(控制时域长度、控制时间步长)之间的映射关系,MPC控制器通过轨迹点匹配,实现实时工况下控制参数的自适应调整,以提高履带车辆在复杂多变工况下的轨迹跟踪精度和稳定性。具体的算法原理,如图5所示。

图5 改进PSO-MLP算法伪代码

3.2 运动基元提取

基于真实驾驶数据对运动基元进行提取和再生成,以表征不同工况下车辆-道路之间复杂的耦合关系,是提升无人驾驶车辆系统适用性的重要途径之一[19-20]。

本文在文献[19]中的运动基元提取思想基础上,在离线状态下基于最优控制理论,根据大量无人履带车辆在实际越野场景下的历史数据,进行运动基元库的生成。在线状态下,根据感知模块提供的栅格地图、全局规划的参考路径以及运动基元库,针对典型工况,轨迹模块基于A*搜索算法进行运动基元的实时拼接和平滑过渡,以得到具备车辆位姿信息以及运动语义信息的参考轨迹:

Sr=[sx,sy,sz,syaw,spitch,sroll,sv,sρ,stype]

(19)

式中:sx、sy、sz为参考轨迹点在车体坐标下的坐标;syaw、spitch、sroll为参考轨迹的车辆三维姿态信息;sρ为参考轨迹的曲率;sv为车辆的参考速度;stype为履带车辆运动基元的类型。

针对环境中具备的几种典型越野工况,规划模块生成的参考轨迹中主要由以下4种运动基元组成:类直线运动基元PS、类小曲率转向运动基元PG、类单移线运动基元PC、类U形弯运动基元PU。图6所示为本文进行轨迹跟踪控制的参考轨迹。

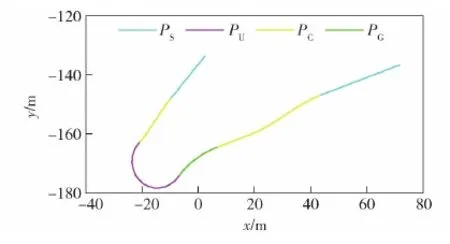
图6 参考路径图Fig.6 Diagram of the reference path

3.3 基于改进PSO算法的最优参数组合提取

对于已经提取出来的包含运动语义信息、车辆状态信息、以及轨迹跟踪响应信息的历史数据集DH,采用改进PSO算法,进行不同运动基元类型下的最优控制参数组合提取,为MLP神经网络模型的训练提供数据基础。将输入到MPC模型的控制时域长度和时间步长大小作为粒子,则粒子的位置可以表达为

(20)

对粒子的位置和速度进行初始化:

(21)

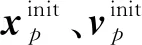
越野工况下,恶劣的环境条件使得硬件处于不良的工作状态,导致MPC的控制量求解时间极不稳定。如果在一个控制周期内,MPC求解器无法求解出最新控制量,会严重威胁行车安全。因此,在对每种运动基元内的最优控制参数进行提取时,PSO算法中适应度函数的设置需要综合考虑车辆的轨迹跟踪精度、稳定性以及计算时间成本。跟踪精度代价项通过横向偏差和航向偏差体现,跟踪稳定性代价项由控制量变化率体现,而计算时间成本代价项则由MPC求解器的迭代求解时间确定,一般来说,迭代求解时间随着控制参数的变化而变化[10]。根据粒子的位置信息,结合履带车辆历史数据集合DH,可以匹配到相应的车辆轨迹跟踪响应状态信息,为适应度函数的评价提供依据。适应度函数的表达形式为

(22)

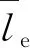
(23)

式中:t、t+1为迭代次数;vp(t)、vp(t+1)分别为第p个粒子在第t、t+1轮迭代的速度;w(t)为第t轮迭代的惯性因子,w(t)>0;c1、c2为学习因子,分别代表认知系数和社会系数,通常c1=c2∈(0,4);r1、r2为(0,1)之间的随机数;Pp(t)为第p个粒子累计到第t轮迭代的局部最优值;xp(t)、xp(t+1)分别为第p个粒子在第t、t+1轮迭代的位置;G(t)为粒子群内所有粒子累计到第t轮迭代的全局最优值。为解决算法早熟以及迭代后期易在最优解附近振荡的情况,这里采用线性可变权重系数的方法进行权重系数的设置:

(24)

式中:wmax、wmin分别为权重系数的最大值和最小值;tmax为最大迭代次数。

在进行状态更新时,需要对位置和速度进行越界修正:

(25)

(26)

式中:vmax为粒子的最大速度;xmin、xmax分别为粒子位置的最小值和最大值。

3.4 基于MLP的最优控制参数预测

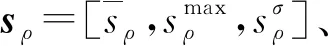
图7 MLP算法原理图Fig.7 Schematic diagram of the MLP algorithm

本文采用学习率自适应优化算法进行MLP神经网络的训练,具体流程如图8所示。

MLP神经网络具体算法流程如下:

步骤1初始化网络深度l、模型权重系数矩阵W(q)、模型的偏置参数b(q)等参数,q∈{1,…,l}。模型的激活函数选择tanh 函数:

(27)

步骤2基于模型输入、模型参数进行模型输出的求解,并得到损失函数L(,y),y为输入x时的神经网络输出真值,为输入x时的神经网络输出预测值。

图8 学习率自适应优化算法流程伪代码表

h(0)=xh(0)=x
h(k)=f(b(k)+W(k)h(k-1)),k∈{1,…,l}
=h

(28)

式中:h(k)为第k层隐藏单元的向量。

步骤3反向传播更新。

未达到迭代终止条件时,需要根据误差的梯度方向对不同网络深度的权重系数矩阵和偏置参数进行更新,然后再重复步骤2,直至达到迭代收敛条件。

将改进PSO算法优化得到的数据集划分为训练集和测试集。训练集的数据用于基于学习率自适应优化算法的MLP神经网络的模型训练,测试集数据用于对模型的精度进行评价,得到如图9所示的预测结果。图9中tstep为时间步长标签值,step为时间步长预测值,tlr为时域长度标签值,lr为时域长度预测值,step、lr可以对tstep、tlr进行良好预测。基于改进PSO-MLP算法,以当前车辆状态、运动基元类型等作为输入,可以对最优控制参数组合进行较好预测。

图9 MLP神经网络预测效果Fig.9 Prediction of the MLP neural network results

4 试验验证

为了验证本文提出的算法框架的有效性,分别进行仿真实验和实车试验。仿真实验由ROS-VREP联合仿真环境测试完成,而实车试验则通过一辆双侧独立电驱动中型无人履带平台完成。试验过程中的平台结构、性能参数如表1所示。

表1 各平台试验参数表

4.1 ROS-VREP联合仿真

仿真实验是对算法初步的功能性验证,用于保证实车测试的安全性,场景如图10所示,平台的具体参数如表1所示,仿真所需的参考轨迹为图6所示的轨迹,仿真过程中的最高车速为20 km/h。为了体现数据真实规律,每组实验重复3次,并选择其中特征最明显的一组作为对照组。

图10 ROS-VREP联合仿真环境Fig.10 ROS-VREP co-simulation environment

基于算法的收敛效果以及轨迹跟踪响应状态,设置对照组如下所示:对照组1设置为tl=2.7 s、ts=0.15 s;对照组2设置为tl=1.2 s、ts=0.10 s;对照组3设置为tl=0.54 s、ts=0.06 s。其中对照组1的时域长度和时间步长最大,计算成本也最大;对照组2与基于双参数自适应优化算法的时间成本相同;对照组3的时域长度和时间步长最小,时间成本最小。

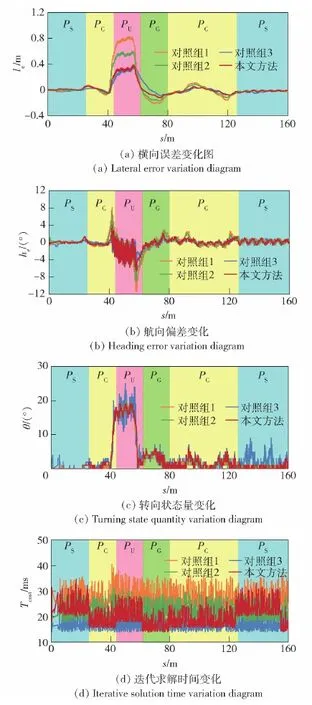
图11 仿真实验轨迹跟踪效果Fig.11 Simulated trajectory tracking performance

表2 仿真实验轨迹跟踪效果统计表

结合图11和表2对轨迹跟踪效果的统计可以看出,对照组1虽然转角状态量变化最为稳定,但轨迹跟踪的精度差,计算载荷大,本文提出的自适应参数优化法相比于对照组1分别降低横向偏差48.9%,降低航向偏差31.4%,节省计算成本23.4%。对照组2的计算时间成本和转角变化率均值几乎一致,但本文算法的轨迹跟踪精度较高,横向偏差和航向偏差仅为对照组2的66.9%、81.7%。对照组3的计算成本最低,跟踪精度也最高,但是车辆的转角平均变化率为本文算法的2.3倍,尤其在PU、PS的运动基元路段,车辆的转角出现了较大的波动,轨迹跟踪处于失稳的状态。本文算法在轨迹跟踪的精度、行驶稳定性、时间成本上做到了较好的均衡。基于ROS-VREP的联合仿真对算法进行了初步的验证,为实车试验的设计提供了重要的参考。

4.2 实车验证

实车试验基于如图12所示的双侧独立电驱动中型无人履带平台开展,平台的具体结构、性能参数如表3所示。平台装配的设备包括:光雷达、GNSS接收机、惯性导航系统、感知工控机、规控工控机以及驱动电机等。搭载的规控工控机的处理器型号为八核八线程的Intel Core i7-9700,GPU型号为Nvidia RTX 2080Ti,内存32 GB,操作系统为Ubuntu 16.04。

图12 无人驾驶履带车辆试验平台Fig.12 Experimental platform of the unmanned tracked vehicle

同样地,对轨迹跟踪控制过程中的不同运动基元的横向偏差均值、航向偏差均值、转角状态量变化率均值以及迭代求解时间进行提取,得到如图13和表3所示的轨迹跟踪效果及数据统计。

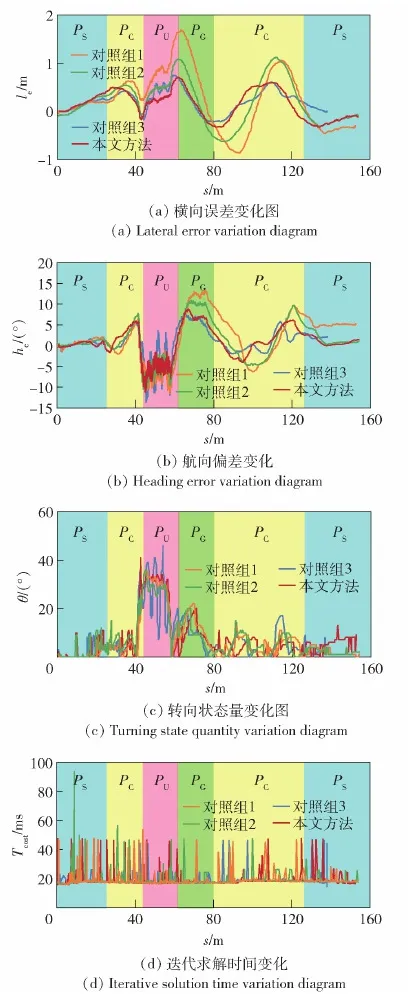
图13 履带车辆试验轨迹跟踪效果Fig.13 Track performance for the unmanned tracked vehicle

表3 实车试验轨迹跟踪效果统计表

通过对不同算法的轨迹跟踪效果的统计分析可以看到,对照组1在全程的转角状态量变化率的均值最小,反映出该组实验的轨迹跟踪稳定性最好,但本文算法在横向跟踪误差、航向跟踪误差以及时间成本上相对于对照组1分别降低34.6%、15.3%、2.7%。

对照组2的时间成本与本文算法相近,但轨迹跟踪的精度和稳定性均较差。本文算法相对于对照组2,横向偏差均值、航向偏差均值以及转角变化率均值可以分别降低30.5%、17.2%、7.8%。对照组3的时间成本最低,轨迹跟踪的精度也最高,但是轨迹跟踪的稳定性是最差的,尤其在PU路段,车辆为了达到较高的跟踪精度,出现了多次摆尾的情况,这无疑将严重影响履带车辆的行车安全。综上,本文提出的算法,在保证车辆具有较高的行驶稳定性、较为经济的计算成本前提下,实现了对参考轨迹的精准跟踪。

5 结论

本文针对模型预测轨迹跟踪控制算法定参数输入下轨迹跟踪效果不稳定的情况,建立了双参数自适应优化与预测模块,为轨迹跟踪控制模块提供自适应参数输入,并进行了ROS-VREP仿真实验、实车试验的算法验证。得出主要结论如下:

1)通过对运动基元类型、轨迹跟踪响应状态,车辆状态以及控制参数进行数据提取,基于改进PSO优化算法,实现了最优参数组合数据集的构建。

2)基于学习率自适应优化算法,结合最优参数组合数据集进行MLP神经网络的模型训练,根据规划模块实时信息和车辆状态实时反馈,对最优控制参数组合进行了良好的预测,实现了为轨迹跟踪控制模块提供时变自适应的控制时域长度、控制时间步长的双参数输入。

3)通过ROS-VREP、实车试验的结果分析,本文提出的算法在保证车辆具有较好轨迹跟踪稳定性、计算成本经济性的前提下,实现了较高的轨迹跟踪精度。实车试验中,与相同计算成本下的定参数轨迹跟踪控制算法相比,横向偏差均值、航向偏差均值以及转角变化率均值可以分别降低30.5%、17.2%、7.8%,验证了本文提出算法框架的有效性和可行性。