融合过滤和相似度计算的高错误率基因组数据敏感序列识别
孙 辉,钟 诚
(广西大学 计算机与电子信息学院,南宁 530004)
(广西高校并行分布式计算技术重点实验室,南宁 530004)
1 引 言
人类基因组测序已经在诸多领域取得了应用.然而,如果基因组数据没有得到有效的保护,那么将会带来很大的隐私泄露风险[1-3].Gymrek等人的研究表明,通过短串联重复序列(STRs)和单核苷酸多态性(SNPs),可以根据基因组数据和个人公开信息发起重识别攻击(RIA),从而导致个人隐私数据泄露[4].基因组数据敏感序列识别是解决DNA数据隐私敏感问题的一个重要手段[5,6].
基因组敏感序列是人类DNA序列中易受隐私攻击影响的核苷酸序列,分为短串联重复序列和疾病相关序列两类[6,7].短串联重复序列是指基本重复单元为1~6bp的串联重复序列[8].由于短串联重复序列在人类遗传变异中占比较大,且容易通过聚合酶链式反应(PCR)扩增,所以短串联重复序列在疾病诊断和人员身份鉴定中具有重要作用.疾病相关序列是指携带疾病易感基因的核苷酸序列[7].由于疾病易感基因翻译成蛋白质可使个体表现出不同的性状,所以疾病相关序列可被用于个体定位.所谓敏感序列识别是指从基因组原始测序数据中识别出以上两类易受隐私攻击影响的DNA敏感序列.通过敏感序列识别,对敏感序列片段给予保护,可以避免个人隐私数据的泄露.
目前已有用于识别短串联重复序列的一些启发式算法REscan[9]、lobSTR[10]和mTR[11]等.然而,这些算法只能识别出部分基因组数据敏感序列,且对高错误率短串联重复序列识别准确性较差.为有效识别基因组数据敏感序列,Cogo等人提出了短序列过滤算法SRF[6].SRF算法的实现依赖于第三方数据库收集的敏感序列和布隆过滤器(Bloom filter)[12,13].针对SRF算法拓展性差、难以识别潜在相似性敏感序列问题,Decouchant等人提出基于k-mer分割的长序列过滤算法LRF,并通过等位基因(allele)变异组合识别具有潜在相似性的敏感序列[7,14].Fernandes等人在LRF算法的基础上,通过连锁不平衡(LD)实现基因组数据敏感序列的多标签分类[15].Lambert等人通过敏感序列识别算法和软件防护扩展技术(SGX)实现了DNA序列的安全比对[16].随着单分子实时测序技术(SMRT)和牛津纳米孔测序技术(ONT)等第3代测序技术的发展,测序平台产生的序列越来越长且具有高错误率的特点[17].
基于多哈希映射的布隆过滤器无法对潜在相似序列产生相同的哈希映射[12].若采用基于布隆过滤器的敏感序列识别算法对高错误率的基因组长序列进行敏感序列识别,则其获得的识别准确率较低.为更有效地识别出基因组数据高错误率长序列中的敏感序列,本文提出一种融合过滤和相似度计算的敏感序列识别算法.本文剩余内容组织如下:第2节将详细阐述如何使用双布隆过滤器避免对重复序列的多次计算以及如何改进相似性度量计算方法以识别敏感序列;第3节给出本文算法和同类算法的实验评估结果;第4节总结本文工作.
2 方 法
设N[0:n-1]表示长度为n的第3代测序序列,本文融合过滤和相似度计算的敏感序列识别方法的过程是:第1步,分割序列N为n-r+1条短序列Rj=N[j:j+r-1],r为Rj的长度,j=0,1,2,…,n-r,n>r;第2步,采取双布隆过滤器方法对短序列Rj进行动态去重,以避免对相同短序列的重复计算,其中布隆过滤器BF1用于敏感序列去重,布隆过滤器BF2用于非敏感序列去重,j=0,1,…,n-r;第3步,对短序列Rj进行短串联重复序列识别,以判断序列Rj是否是短串联重复序列,若Rj是短串联重复序列,则将Rj映射定位存储至布隆过滤器BF1位数组B1,j=0,1,2,…,n-r;第4步,将短序列Rj与GWAS Catalog数据库疾病敏感序列进行计算比对,以判断Rj是否是疾病相关序列,若Rj是疾病相关序列,则将Rj映射定位存储至布BF1位数组B1,否则将Rj映射定位存储至BF2位数组B2,j=0,1,2,…,n-r;第5步,根据短序列R0,R1,…,Rn-r的敏感识别结果res[0:n-1],生成序列N[0:n-1]的两条掩码序列Npub[0:n-1]和Npri[0:n-1]作为算法识别结果.图1描述了本文方法的处理流程.
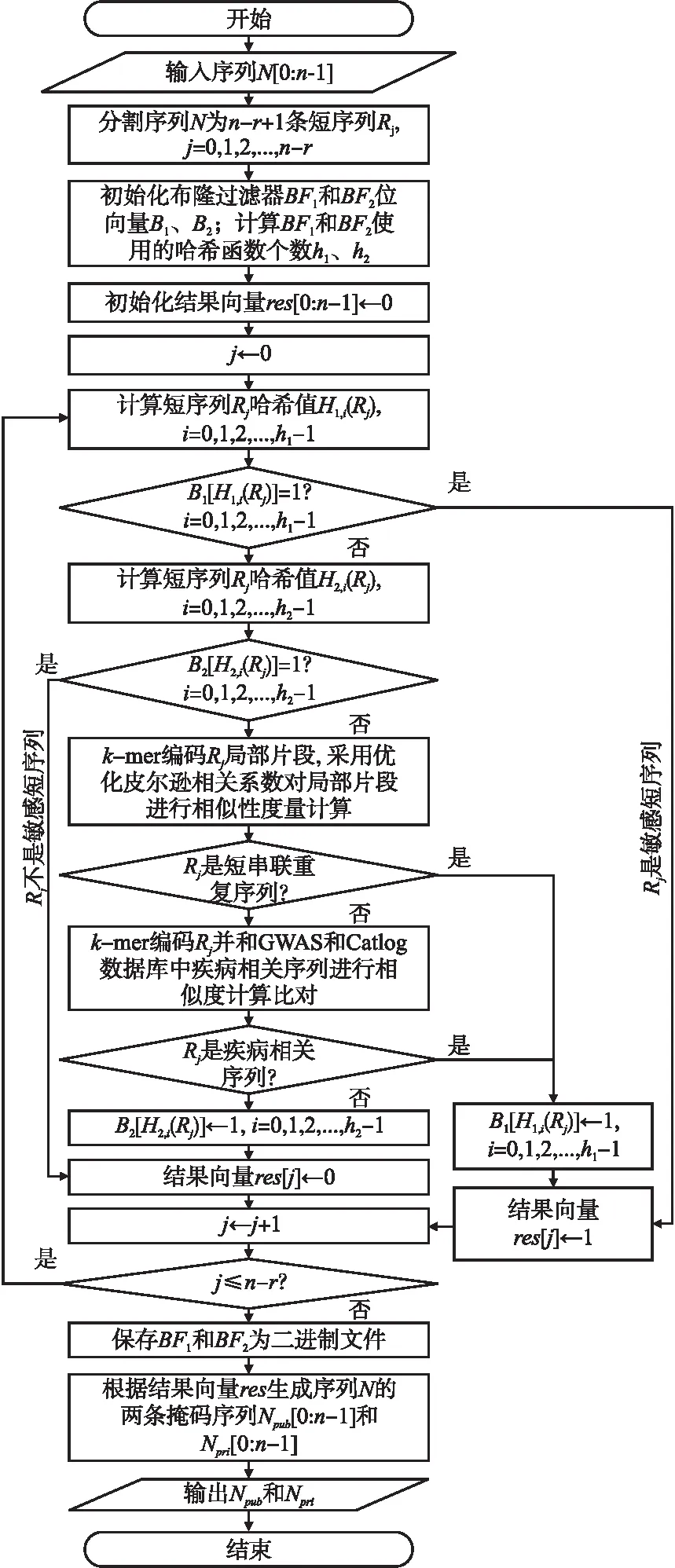
图1 本文识别方法的处理流程
在图1中,结果向量res[0:n-1]用于记录每条短序列Rj的敏感序列识别中间结果;为保存算法最终识别结果,本文采用类似于文献[7]的方法,根据结果向量res[0:n-1]生成序列N[0:n-1]的两条掩码序列Npub[0:n-1]和Npri[0:n-1],其中Npub表示掩码非敏感序列,Npub中的敏感序列片段将以“*”掩码,Npri表示掩码敏感序列,Npri中的非敏感序列片段将以“*”掩码.通过生成掩码序列,对掩码敏感序列进行隐私保护,以避免针对基因组数据的隐私攻击.
下面详细阐述融合过滤和相似度计算的高错误率敏感核苷酸序列识别方法.
2.1 序列分割
为识别测序长序列中的敏感序列,采取滑动窗口策略将长序列N[0:n-1]分割为n-r+1条、每条长度为r的短序列Rj=N[j:j+r-1],其中Rj和Rj+1共享重叠的r-1个核苷酸,以确保每条短序列敏感识别的准确性,j=0,1,2,…,n-r,n>r.
人类DNA序列中,约有99.5%的序列具有高度一致性,只有0.5%的核苷酸记录个体独有信息[6].将长序列分割为短序列,会产生大量相同短序列.若对所有短序列均进行敏感序列识别,则将耗费许多计算资源.为避免对相同短序列的重复计算,本文利用布隆过滤器对分割得到的序列去重.
2.2 序列去重
布隆过滤器由一个二进制向量和若干哈希函数组成[14].基于多哈希映射的布隆过滤器可以降低哈希冲突的影响.
2.2.1 初始化布隆过滤器
设布隆过滤器BF1和BF2分别用于敏感序列和非敏感序列去重,其位向量分别为B1[0:b1-1]和B2[0:b2-1],使用哈希函数的个数分别为h1和h2.初始化布隆过滤器,需计算位向量B1和B2的规模b1和b2[12]:
(1)
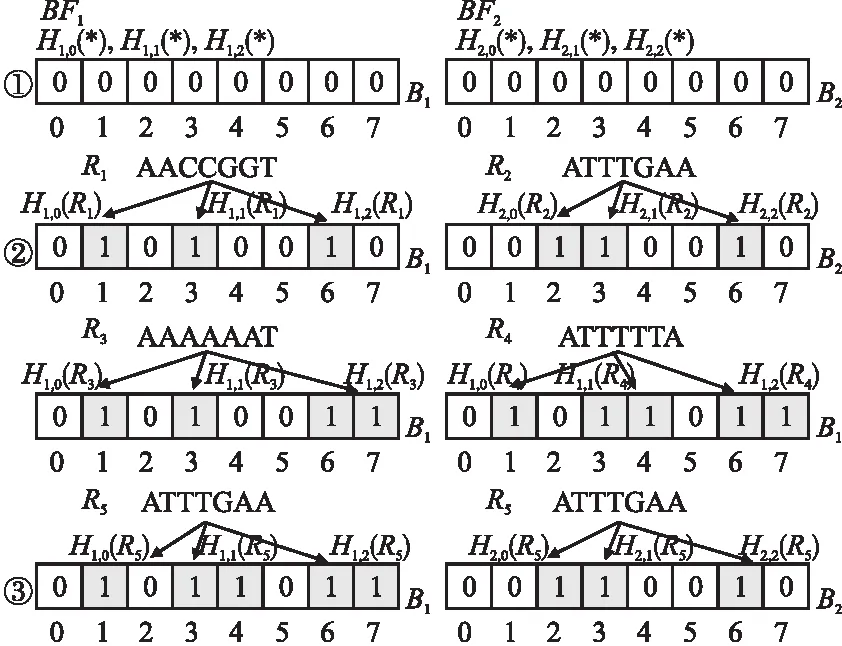
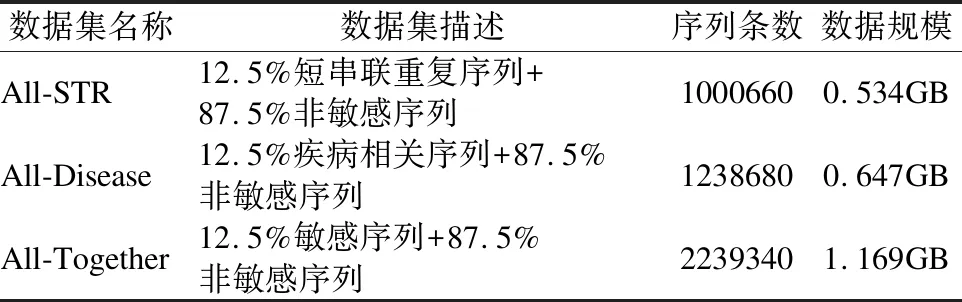
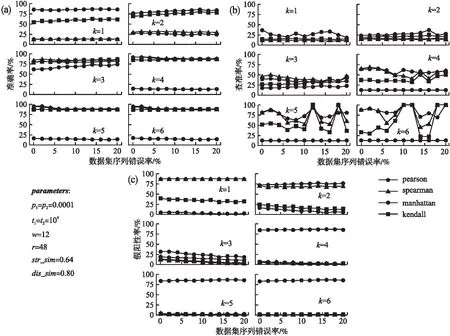
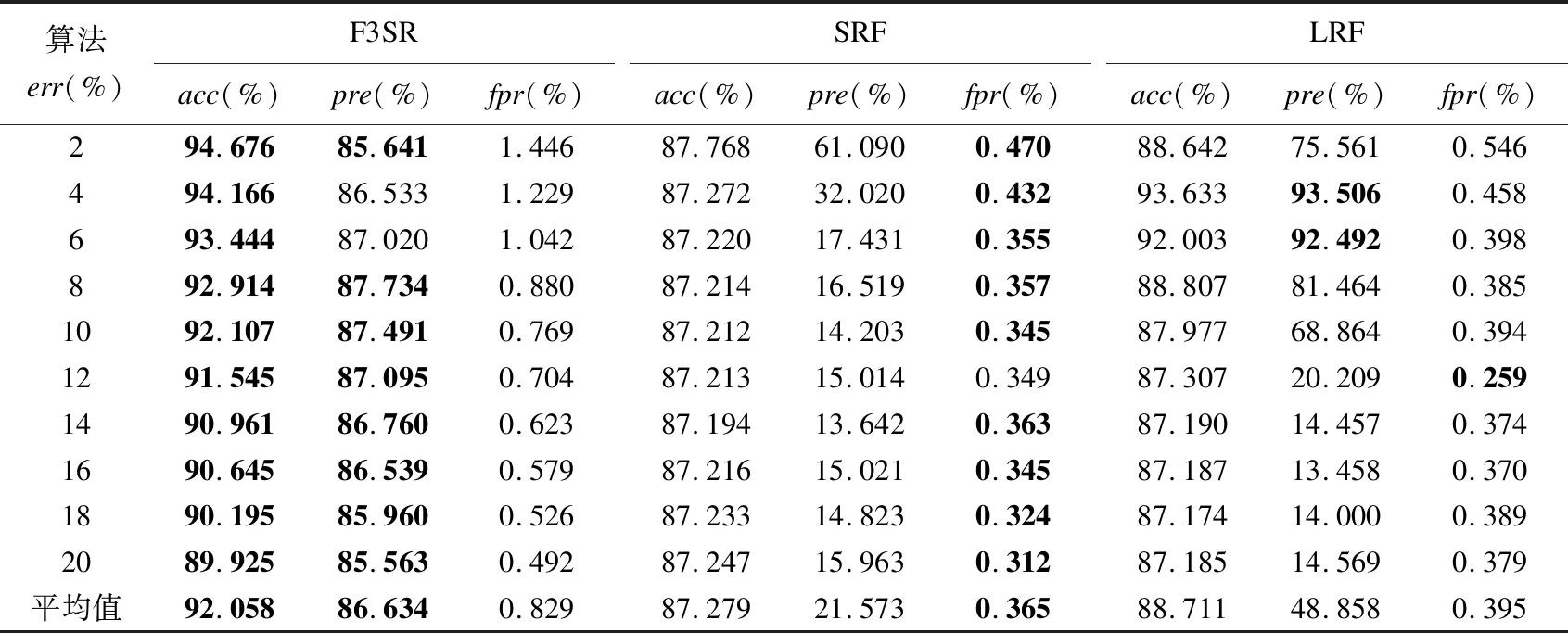
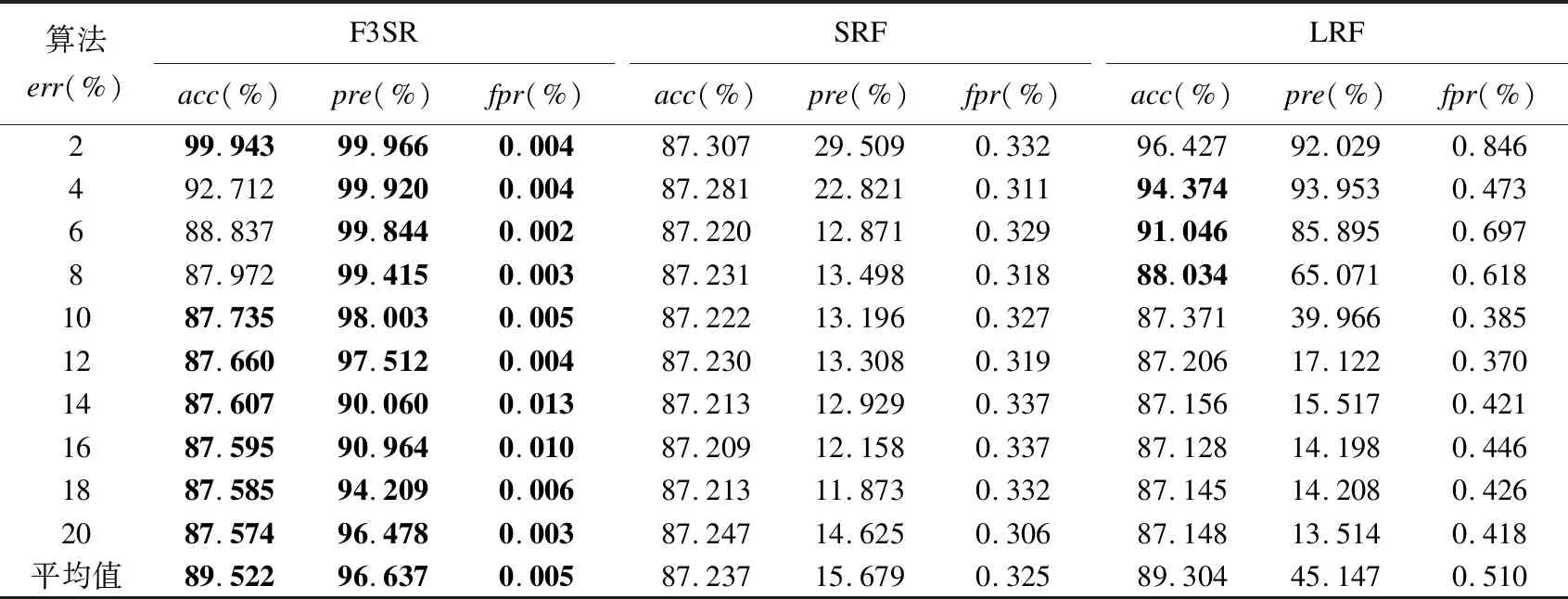
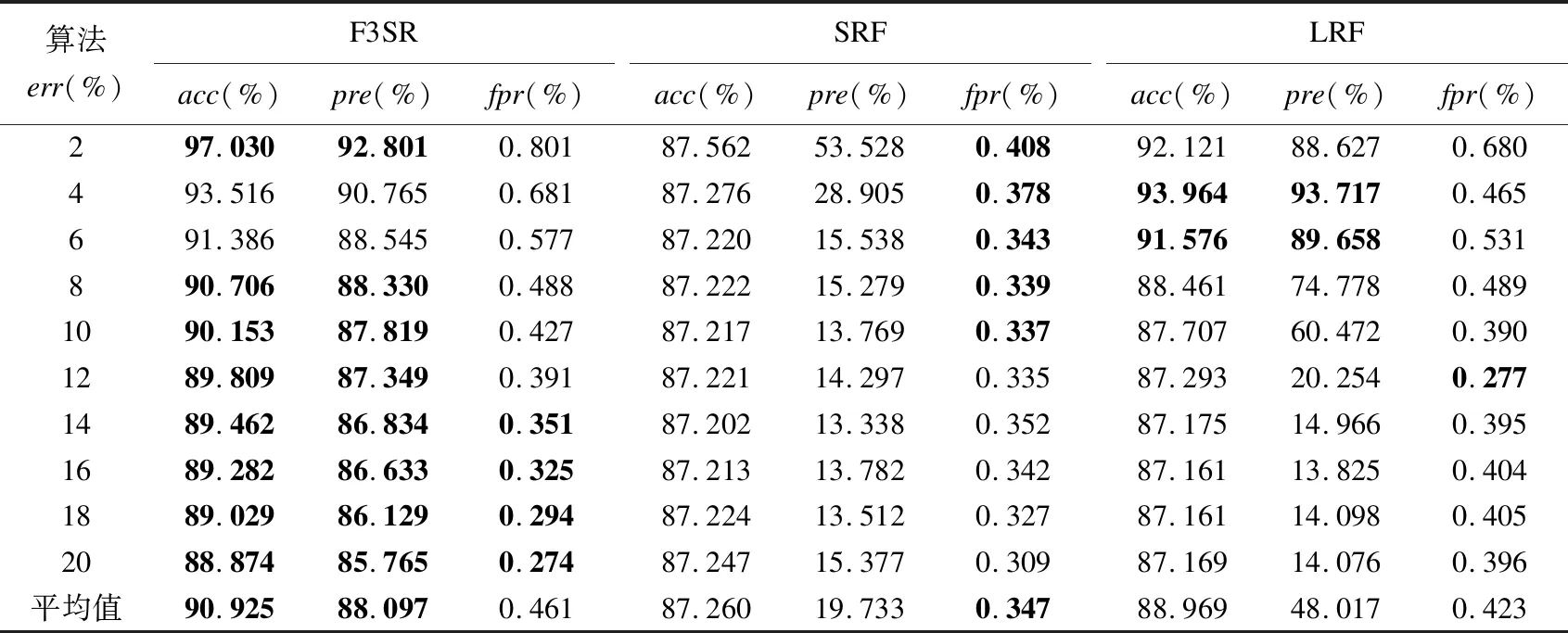
式(1)中,ti表示布隆过滤器BFi可容纳序列数量的上限,pi表示误报率,BFi位向量规模bi和可容纳序列数量的上限ti呈正相关,bi和误报率pi(0 (2) 在计算出b1和b2,h1和h2之后,置B1,i=0、B2,k=0,i=0,1,2,…,b1-1,k=0,1,2,…,b2-1. 2.2.2 短序列去重 对短序列Rj去重,需要根据已知短序列Rk的识别结果将Rk映射定位存储至对应布隆过滤器,k=0,1,2,…,j-1.若Rk为敏感短序列,则对Rk进行h1次哈希计算得到h1个哈希值H1,i(Rk),并将布隆过滤器BF1中位向量B1[H1,i(Rk)]置为1,i=0,1,2,…,h1-1.若Rk为非敏感短序列,则对Rk进行h2次哈希计算得到h2个哈希值H2,i,并将布隆过滤器BF2中位向量B2[H2,i(Rk)]置为1,i=0,1,2,…,h2-1. 若要判断Rj是否是一条重复序列,首先对Rj进行h1次哈希计算,得到h1个哈希值H1,i(Rj),并在BF1中的位向量B1进行查询,若B1[H1,i(Rj)]均为1,i=0,1,2,…,h1-1,则Rj是一条重复短序列,且是敏感短序列,此时置res[j]=1.若B1[H1,i(Rj)]不全为1,则对Rj进行h2次哈希计算,得到h2个哈希值H2,i(Rj),并在BF2中的位向量B2进行查询,若B2[H2,i(Rj)]均为1,i=0,1,2,…,h2-1,则Rj是重复短序列,且是非敏感短序列,此时置res[j]=0.若B2[H2,i(Rj)]不全为1,则说明Rj不存在于BF1或BF2中,Rj不是一条重复序列,需要对Rj执行短串联重复和疾病相关序列识别处理. 为更好体现算法去重思想,图2给出序列去重示例. 图2 布隆过滤序列去重示例 在图2中,BF1和BF2的位向量B1和B2均是一个8位的二进制向量;BFi序列去重使用3个哈希函数Hi,0、Hi,1和Hi,2,i=1,2;R1、R3和R4是敏感短序列,R2和R5是非敏感短序列,且R5是重复短序列(R5=R2),为此去重序列R5.首先,初始化布隆过滤器BF1和BF2的位向量B1、B2均为0,此时BF1和BF2均为空,没有记录任何短序列信息.然后,将R1~R4映射定位存储至BF1和BF2的位向量B1和B2;此时B1第1,3,4,6,7位被设置为1,B2第2,3,6位被设置为1.最后,序列R5通过BF1进行敏感序列去重时所产生的3个哈希标记不全为1.因此需要经过BF2进行非敏感序列去重;此时对R5进行哈希映射所产生的3个哈希值在BF2中标记均为1,因此R5是重复短序列,且R5由BF2过滤出,所以R5是非敏感短序列.通过双布隆过滤器处理可知序列R5为非敏感短序列,因此,不需要执行后续短串联重复序列和疾病相关序列识别操作. 通过对短序列执行双布隆过滤器去重操作,可避免对短序列的重复计算.若短序列不存在于布隆过滤器BF1或BF2,则需要对短序列进行短串联重复序列识别. 设Σ={A,C,G,T}表示组成DNA序列的符号集,Σ+表示Σ上的非空字符串集,对于序列u∈Σ+,一个理想的短串联重复序列可表示为[u]q,其中q表示序列u的重复次数,|u|表示序列u的长度且1bp≤|u|≤6bp,u为最小基本重复单元[8].短串联重复序列的内部重复结构表明,通过合理分割短串联重复序列可以得到记录短串联重复序列基本重复单元的相同子段[11].为此,借鉴文献[11]的思想,本文采用以下步骤判断短序列是否是含有“插入”、“删除”、 “替换”错误的短串联重复序列: 第1步.等长度分割短序列Rj为4个长度为w的短片段,Wj={Wj,1,Wj,2,Wj,3,Wj,4},j=0,1,2,…,n-r; 第3步.计算短序列Rj局部片段Wj,2和Wj,3的相似度sim(Wj,2,Wj,3),并根据短串联重复序列相似度阈值str_sim判断Rj是否为短串联重复序列,若Rj为短串联重复序列,则置结果向量res[j]=1,j=0,1,2,…,n-r. sim(Wj,2,Wj,3)= (3) 图3给出本文方法识别短串联重复序列的示例. 图3 短串联重复序列识别示例 从图3中可知,通过上述步骤计算出第2、3个短片段的相似性达92.79%,大于给定的判别阈值str_sim=0.64,因此R是一条短串联重复序列. 通过对Rj中的两个局部片段统计k-mer词频,可以提取Rj的k-mer统计特征.若Rj具有较少的“插入”、“删除”、“替换”错误,通过k-mer编码Rj的局部片段,可以确保局部片段词频具有较高的一致性,从而可以计算得到较高的相似度值,进而识别Rj是否是具有潜在相似性的高错误率的短串联重复序列,j=0,1,2,…,n-r. 通过对序列结构分析处理可以识别出DNA序列中包含的短串联重复序列.除了短串联重复序列,DNA序列中还可能包含有疾病相关序列.为识别短序列Rj是否是疾病相关序列,本文通过构建敏感序列词典,检索与Rj碱基含量相似的第三方数据库中的疾病相关序列,采用皮尔逊相关系数对Rj和检索到的疾病相关序列进行相似度计算比对,以识别出高错误率疾病相关序列,j=0,1,2,…,n-r. 2.4.1 构建敏感序列词典 构建敏感序列词典的目的是为了降低大量短序列与疾病相关序列相似度计算的代价.本文使用二维数组DICTI[m][4k+3]表示敏感序列词典,其中m表示从第三方数据库提取的疾病相关序列的数量,k为采用k-mer编码核苷酸序列的k值.构建敏感序列词典的方法是: 2.4.2 碱基含量相似性检索 构建敏感核苷酸序列词典之后,对Rj进行碱基含量相似性检索,以进一步降低Rj和敏感序列词典中的序列相似度计算的工作量.文献[11]的研究表明,潜在相似性序列具有碱基含量的一致相似性.序列Rj中G、C、A碱基含量GCARj=[GRj,CRj,ARj],本文采用式(4)的条件,在DICTI中检索与Rj具有碱基含量相似的序列Di: 1-|GCARj[e]-GCADi[e]|≥dis_sim (4) 式(4)中,i=0,1,2,…,m-1,j=0,1,2,…,n-r,e=0,1,2,dis_sim表示疾病相关序列识别相似度阈值.设queryB为通过序列碱基含量相似性检索得到短序列Rj和Di满足式(4)条件的Di下标集合,则queryB=[q0,q1,…qv,…,qt],其中qv为DICTI中碱基含量相似序列的下标,t≤m-1. 2.4.3 疾病相关序列相似度计算 (5) 当序列中含有“插入”、“删除”、“替换”错误时,采用k-mer编码短序列,其差异只体现在变异核苷酸相邻k个碱基处,通过合理取值k,可有效提取高错误率疾病相关序列碱基统计特征.将短序列Rj和第三方数据库疾病相关序列进行相似度计算,通过设置相似度阈值从而可以识别出和第三方数据库具有较高相似性的疾病相关序列. 设待识别长序列为N[0:n-1]、滑动窗口策略分割短序列Rj的窗口长度为r、双布隆过滤器误报率分别为p1和p2、初始化双布隆过滤器可插入最大序列数目分别为t1和t2、k-mer编码取值为k、短串联重复序列识别相似度阈值为str_sim、疾病相关序列识别相似度阈值为dis_sim、参考基因组为HG、GWAS Catlog数据库中疾病相关序列数据集为diseaseData(包含m组数据). 算法1形式描述了融合过滤和相似度计算的高错误率敏感序列识别算法(简记为F3SR算法). 算法1. F3SR 输入:N[0:n-1],r,p1,p2,t1,t2,k,str_sim,dis_sim,HG,diseaseData 输出:序列N识别结果的两条掩码核苷酸序列Npri,Npub Begin 1.依据p1,p2,t1和t2初始化布隆过滤器BF1和BF2位数组B1和B2; 2.依据diseaseData,r,HG和k构建敏感序列词典dicti[m,4k+3]; 3.res[0:n-1]←0; 6.forj=0ton-rdo 7.Rj←N[j:j+r];//提取第j条短序列Rj 8. 对序列Rj执行h1次哈希计算得到h1个哈希值H1,0(Rj),H1,1(Rj),…,H1,h1-1(Rj); 9.ifBF1中B1[H1,0(Rj)],B1[H1,1(Rj)],…,B1[H1,h1-1(Rj)]的值全为1then 10.res[j]←1; 11. 对序列Rj执行h2次哈希计算得到h2个哈希值H2,0(Rj),H2,1(Rj),…,H2,h2-1(Rj); 12.elseifBF2中B2[H2,0(Rj)],B2[H2,1(Rj)],…,B2[H2,h2-1(Rj)]的值全为1then 13.res[j]←0; 14.else//编码短序列局部片段 19.c←1; 20.else 21.c←0; 22.endif 24.ifsim(Wj,2,Wj,3)≥str_simthen 25.res[j]←1; 26. 将B1[H1,0(Rj)],B1[H1,1(Rj)],…,B1[H1,h1-1(Rj)]的值置为1; 27.else 28. 依据短序列Rj的GAC碱基含量对dicti进行相似性序列检索以获得queryB; 29.ifqueryB=∅then 30.res[j]←0; 31. 将B2[H2,0(Rj)],B2[H2,1(Rj)],…,B2[H2,h2-1(Rj)]的值置为1; 32.else 34.fori=0 to |queryB|-1do 37.ifsim(Rj,Di)≥dis-simthen 38.res[j]←1; 39. 将B1[H1,0(Rj)],B1[H1,1(Rj)],…,B1[H1,h1-1(Rj)]的值置为1; 40.goto(6); 41.endif 42.endfor 43.res[j]←0; 44. 将B2[H2,0(Rj)],B2[H2,1(Rj)],…,B2[H2,h2-1(Rj)]的值置为1; 45.endif 46.endif 47.endif 48.endfor 49.保存布隆过滤器BF1和BF2为二进制文件; 50.Npub←N[0:n-1];//初始化掩码非敏感序列 51.Npri←N[0:n-1];//初始化掩码敏感序列 52.beginPos← 0; 53.whilebeginPos 54.ifres[beginPos]≠1then 55.beginPos←beginPos+1; 56.else 57.fori=beginPostobeginPos+rdo 58.ifres[beginPos+r-i]=1andi≠beginPos+rthen 59.forj=beginPostobeginPos+r-ido 60.Npub[j]←‘*’; 61.endfor 62.beginPos←beginPos+r-i; 63. goto(53); 64.elseifi=beginPos+rthen 65.forj=beginPostobeginPos+rdo 66.Npub[j]←‘*’; 67.endfor 68.beginPos←beginPos+r; 69. goto(53); 70.endif 71.endfor 72.endif 73.endwhile 74.forj=0ton-1do //根据掩码序列Npub生成掩码敏感序列Npri 75.ifNpub[j]≠‘*’then 76.Npri[j]←‘*’; 77.endif 78.endfor End. 算法F3SR步1初始化布隆过滤器时间为O(1);步2构建敏感序列词典所需时间为O(m×r×4k);步3初始化结果向量的时间为O(n);步4~步5计算布隆过滤器哈希函数个数时间为O(1);步34~步42最坏情况下所需的时间为O(m×4k);步6~步48时间为O(max(n×h1,n×h2,n×r×4k,n×4k,n×m×4k));步49保存二进制文件时间为O(1);步50~步51初始化掩码序列的时间为O(n);步52~步73生成掩码非敏感序列的时间为O(n×r2);步74~步78生成掩码敏感序列的时间为O(n).由于k、r、m、h1和h2均为某个常数,所以算法时间复杂度为O(n). 算法F3SR通过k-mer编码对DNA序列进行词频统计,将待识别序列中每个核苷酸的邻接信息进行有效提取.由于相似序列的差异只体现在差异核苷酸的局部序列片段,通过k-mer编码可以使具有相似性的核苷酸序列保持词频的整体一致性,通过皮尔逊相关系数可计算出较高相似度得分的序列,所以可以识别出高错误率的敏感核苷酸序列.此外,基于“序列过滤”的思想,算法始终避免对重复序列的计算,有效提升了算法的效率. 实验在设立于广西大学的国家高性能计算中心南宁分中心(2)https://hpc.gxu.edu.cn的Sugon 7000A超级并行计算机系统上进行,使用的计算节点配置为2×Intel Xeon Gold 6230处理器、512GB内存以及8×900GB外部存储空间,运行操作系统CentOS7.4.采用C++语言编程实现算法,布隆过滤器实现参考自ArashPartow(3)https://github.com/ArashPartow/bloom实现的混合hash版本. 本文采用GWAS Catalog数据库[18]全基因组关联研究数据集gwas_catalog_v1.0.tsv构建敏感序列词典,该数据集包含HIV-1 replication、Opioid sensitivity等4680种疾病,共计216250组数据.每组数据包含疾病名称DISEASE、染色体编号CHR_ID、染色体位置CHR_POS等34个标识信息.实验数据采用的参考基因组为NCBI(4)https://www.ncbi.nlm.nih.gov开放下载的人类基因组HG38.实验所用的短串联重复序列来自TRDB数据库(5)https://tandem.bu.edu,疾病易感基因来自GWAS Catalog数据库(6)https://www.ebi.ac.uk/gwas.参照文献[6]的数据预处理规则,预处理每条序列长度为50bp的3个基准数据序列集,每个基准数据集的敏感序列和非敏感序列的数量比例为1∶7,实验数据信息如表1所示. 表1 实验数据集信息 为获得含有错误信息的序列数据集,采用表1数据集作为基准序列,通过随机执行“插入”、“删除”、“替换”操作产生10组错误率为2%~20%的DNA序列进行实验.实验将本文算法F3SR与同类算法SRF[6]和LRF[7]进行测试比较识别的准确率(accuracy,acc)[6]、查准率(precision,pre)[19]和假阳性率(falsepositiverate,fpr)[7]: (6) (7) (8) 其中,TP表示算法识别出真实敏感序列的总数、TN表示识别出真实非敏感序列的总数、FN表示将敏感序列误识别为非敏感序列的总数、FP表示将非敏感序列误识别为敏感序列的总数.准确率反映算法的整体识别结果,准确率越高算法识别效果越好.查准率反映真实敏感序列和算法识别出的敏感序列的比率,查准率越高算法越好.假阳性率反映数据中非敏感序列被误识别为敏感序列的比率,假阳性率越低越好. 为使得采用布隆过滤器对序列去重时具有较低的假阳性率,本文采用文献[14]布隆过滤器实验参数pi=0.0001对布隆过滤器初始化,并设置布隆过滤器容纳序列数量上限ti=104,当实际插入序列的数目超过ti时,动态扩充布隆过滤器的容纳上限为当前上限的2倍,i=1,2. F3SR算法判别短序列Rj是否为短串联重复序列时,需要对Rj第2和第3个短片段进行k-mer编码.通过对TRDB数据库短串联重复序列检索,TRDB数据库中短串联重复序列长度最短为25bp[20],为使得F3SR算法可以准确识别短串联重复序列,F3SR算法取w=12bp.此时,滑动窗口策略分割短序列Rj的长度r=4w=48bp. 设err表示测序引入的错误率,第三代测序错误率高达10~20%[11],考虑测序过程引入最大错误率err=20%,算法相似度阈值t应满足t=1-max(err)=0.8,因此短串联重复序列识别相似度阈值str-sim≤t2=0.802=0.64,疾病相关序列识别相似度阈值dis-sim=t=0.80. F3SR算法通过k-mer编码提取序列统计特征.为选取合适的参数k和相似性度量方法,本文通过实验测试k-mer编码k取值、数据集序列错误率err和皮尔逊相关系数(pearson correlation coefficient)、斯皮尔曼等级相关系数(spearman′s rank correlation coefficient)、曼哈顿距离(manhattan distance)、肯德尔一致性系数(kendall′s consistency coefficient)对F3SR算法识别性能的影响.实验结果如图4所示. 图4 All-Together数据集上错误率、k值和相似性度量方法对算法F3SR的准确率、查准率和假阳性率的影响 在图4中,横坐标表示数据集序列的错误率err(%),err=0表示序列未携带“噪声数据”,err=20表示当前基准数据集中每条序列含有“插入”、“删除”和“替换”错误的比例约为20%.图4的结果表明:当k≥4时算法采用pearson相关系数整体上具有最高的识别准确率和识别查准率,最低的识别假阳性率,其次是spearman等级相关系数和kendall一致性系数,算法采用manhattan距离度量相似度时,整体上识别准确率和查准率最低,且具有较高的识别假阳性率.当k取值4~6时,本文算法识别准确率、查准率和假阳性率趋于平稳.为使F3SR算法在保持较低识别假阳性率的同时具有较高识别准确率和查准率,选取k=5进行k-mer编码. 为评估算法在不同错误率err的序列数据集上运行的识别性能,实验测试了算法F3SR和SRF[6]、LRF[7]在All-STR数据集上运行的准确率acc、查准率pre和假阳性率fpr,实验结果如表2所示. 表2 算法F3SR、SRF和LRF在All-STR数据集上运行的准确率、查准率和假阳性率 表2实验结果表明,F3SR算法在数据集All-STR上运行的识别准确率均高于算法LRF和SRF,且数据集序列的错误率越低算法的识别准确率越高,即使错误率达到20%时仍具有89.925%的较高准确率.这是因为错误率越低的短串联重复序列在分割成序列片段时,越能保证局部片段的词频统计一致性,通过对局部片段进行相似性度量便可以得到较高的局部相似度值,从而使得算法识别序列中短串联重复序列的准确率较高.F3SR算法在All-STR数据集上运行的识别查准率均高于SRF算法;当All-STR数据集序列的错误率为4%~6%时,F3SR算法的查准率略低于LRF算法;当序列的错误率为2%、8%~20%时F3SR算法的查准率高于LRF算法.这表明在高错误率的序列数据集上识别短串联重复序列时,F3SR算法比其他两个算法更有效.与算法LRF和SRF相比,F3SR算法在All-STR数据集上逆行的假阳性率最高;这是因为对短序列局部片段进行相似性度量识别短串联重复序列时,若短序列的局部片段具有极高相似性但并不是短串联重复序列时,算法产生了错误判别. 在All-STR数据集上的实验表明,F3SR算法可以有效识别高错误率的短串联重复序列. 为评估F3SR算法是否可以有效识别疾病相关序列,实验测试了算法F3SR、SRF[6]和LRF[7]在不同错误率err的序列数据集All-Disease上的识别性能,实验结果如表3所示. 表3 算法F3SR、SRF和LRF在All-Disease数据集上运行的准确率、查准率和假阳性率 从表3可以看到,当All-Disease数据集中序列错误率为2%~20%时:无论是某种具体错误率情形还是平均情况,F3SR算法整体上具有最高的识别准确率和查准率,LRF算法具有第2高的识别准确率和查准率,SRF算法的识别准确率和查准率最低;F3SR算法在All-Disease数据集上识别假阳性率最低,其次是SRF和LRF算法. 在All-Disease数据集上的实验表明,相较于SRF和LRF算法,F3SR算法识别疾病相关序列时,具有更高的准确率和查准率,具有最小的识别假阳性率,整体上识别效果较好. 为评估在既有短串联重复序列又有疾病相关序列的数据集上运行算法的识别性能,本文进一步测试了3种算法在序列含有不同错误率err的真实混合数据集All-Together上的算法识别性能,实验结果如表4所示. 表4 算法F3SR、SRF和LRF在All-Together数据集上运行的准确率、查准率和假阳性率 表4结果表明,对于各种错误率的序列,与算法SRF和LRF相比,F3SR算法在All-Together数据集上运行时,整体上获得最高的识别准确率和查准率.在假阳性率方面,对于错误率2%~12%的序列数据集,本文算法略低于LRF和SRF算法;对于错误率14%~20%的序列数据集,本文算法具有最低的假阳性率.算法F3SR相较于LRF和SRF,在错误率2%~20%的数据集All-Together平均识别准确率分别提高1.96%和3.66%,平均查准率分别提高40.08%和68.36%,平均假阳性率分别高了0.114%和0.038%. 综上所述,相较于SRF和LRF算法,本文算法F3SR在3个数据集上运行时,整体上具有更高的识别准确率和识别查准率,可有效识别具有潜在相似性的高错误率基因组数据敏感序列. 通过将长序列分割为多条短序列,对每条短序列采取双布隆过滤方法进行序列去重,可避免对每条短序列的重复计算;采用k-mer编码策略对短序列进行词频统计可提取具有潜在相似性序列的碱基统计特征,通过改进序列相似度计算比对方法,可有效识别具有高错误率的敏感序列,使得识别算法获得更高的识别准确率和查准率.融合长序列分割、过滤和相似度计算的方法可以有效识别出高错误率敏感序列,但算法需要花费一些时间与第三方数据库敏感序列进行相似度计算比对,这对于序列长度越来越长的大规模测序数据集上运行的时间开销较高.如何设计并行计算方法加速长序列中敏感序列的识别过程,以适应大规模基因组测序数据应用,将是下一步的研究工作.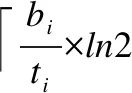
2.3 短串联重复序列识别

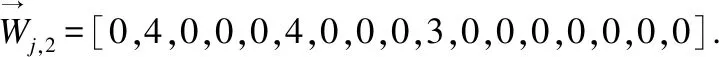
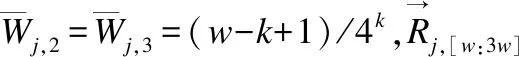

2.4 疾病相关序列识别
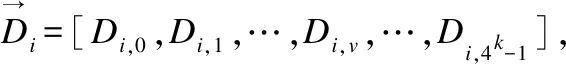

2.5 识别算法

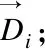
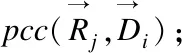
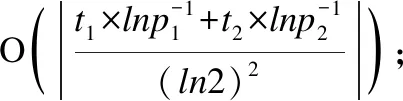
3 实 验
3.1 实验环境与数据
3.2 算法参数选取
3.3 算法比对实验
4 总 结

