语言隐喻的认知博弈论语用学分析
徐慈华 严小姗
1 绪论
自亚里士多德以来,隐喻一直因其独特的修辞功能而深受重视。传统的观点一直认为,隐喻是一种修饰性的语言现象,也是文学中常用的表现手法。但20 世纪80 年代以来,隐喻研究发生了认知转向。随着学者们实证研究和理论探索的深入,我们对隐喻的看法发生了根本的变化。隐喻普遍存在于我们日常生活的各个领域,它不仅是一种语言上的修饰,还是一种重要的认知机制,并且无时无刻不在影响我们概念体系的建构以及与之对应的行为方式。([10])在诸多解释隐喻现象的理论中,关联理论对隐喻使用所做出的解释是一种颇具竞争力的方案。该方案基于“特设概念(ad hoc concept)”和“关联原则(principle of relevance)”这两个重要的概念工具,指出隐喻理解是关联引导下的词汇扩大推理。虽然关联理论分析了隐喻理解的推理过程和限制条件,但其总体上依旧是描述性的,或者说属于一种局部的形式化。本文的目标是运用近年来日趋成熟的博弈论语用学,依托其中的IBR(Iterated Best Response)模型,为该解释方案提供一个系统完整的形式化表征。
本文的第2 部分,回顾了关联理论对语言隐喻的基本看法,在对“特设概念”和“关联原则”进行详细说明的基础上,结合具体的隐喻案例,分析了关联理论是如何对语言隐喻作出解释的,以及关联理论在其形式化分析刻画隐喻时存在的局限性。第3 部分探讨了信号博弈分析框架所涵盖的诸多重要交际因素,并介绍了IBR 模型的求解思路,论证了运用博弈论语用学的方法和工具对关联理论的描述分析过程进行形式化的可行性。第4 部分基于第2 部分关联理论对语言隐喻的分析,用IBR 模型对其进行形式化的建构和求解,并运用这一形式化分析工具系统性地解释隐喻发出者是如何利用不同语境中接收者所拥有的概率性信念来实现某些特定的交际目标的。最后,我们总结本文核心观点,指出本研究的局限之处,并为后续的探索提供方向性建议。
2 语言隐喻的关联理论解释
关联理论认为,语言隐喻(linguistic metaphor)源于语言交际,它是一种宽泛使用的语言。([16])正如斯珀波(D.Sperber)和威尔逊(D.Wilson)所说,我们把隐喻简单看作是一个包含字面含义、宽泛用法和夸张解释的连续统一的系列案例。([15])在我们看来,隐喻解释与其他的语言解释方式完全一致,并不存在专门针对隐喻的特定机制和只适用于隐喻的有趣归纳。为了对这个连续系统中的诸类语言现象作出统一的解释,关联理论结合词汇语用学提供了两个十分重要的分析工具:“特设概念”和“关联原则”。下文将在对这两个概念进行详细说明的基础上,结合具体的语言隐喻案例,分析关联理论是如何解释语言隐喻的。
2.1 特设概念和关联原则
语言的理解至少涉及解码和推理两个基本过程。就词汇的使用而言,其过程可以描述为:听话人在接收到一个词后,会对这个词进行解码以获得词汇意义,并将这个词汇意义作为线索推导出说话人的意义。因此,词汇语用学的目标就是解释词汇意义是如何在交际过程中做出调整的。([16],第184 页)这里主要涉及两种不同类型的调整,即词汇缩小(lexical narrowing)和词汇扩大(lexical broadening)。词汇缩小指的是一个词传递了比它编码的意义还要具体的意义,形成了更小的外延。而词汇扩大指的是用一个词传递比解码获得的意义更具概括性的意义,从而扩大了具体语言的外延。([17],第238 页)不管词汇缩小,还是词汇扩大,我们都可以用下面这个公式表达:
在上面这个公式中,一个词语经过解码形成一个反映字面意义的概念[CONCEPT]。这个[CONCEPT]为进一步的推理提供线索。在语境的作用下,通过词汇缩小或扩大,形成一个具体情境中恰当的概念[CONCEPT*],我们称之为特设概念。威尔逊和卡特森(R.Cartson)指出,词汇理解中尤其会涉及一个特设概念或具体情景意义的建构,该过程基于编码概念、语境信息和语用期待的原则。([17],第246 页)
在词汇语用学中,特设概念是有着坚实心理学依据的分析工具。美国认知心理学家巴斯劳(L.Barsalou)在对范畴化现象的研究中指出,原型缩小(prototypical narrowing)比我们想象得更要灵活,并且更具有语境依赖性([1])。心理学家格鲁克斯伯格(S.Glucksberg)在隐喻研究中发现了类似于词汇扩大的现象([9])。他指出隐喻是一种范畴归属性断言(category-inclusion assertion),喻体词具有双重指称:一个是字面上的指称,另外一个是以字面指称为典型代表的一类事物或情境。隐喻的理解具有强语境依赖性,从关联理论的角度看,隐喻理解中产生的以字面指称为典型代表的那类事物或情境就是一个用于描述隐喻本体、赋予隐喻本体以特定属性的特设概念。([9,21])
语用学的目标是要解释听话人如何从话语和语境提供的线索中推出说话人的意图([16],第184 页)。特设概念的提出虽然描述了词汇理解过程中个体百科知识的激活和选择过程,但没有说明是什么触发了特设概念的建构,是什么决定了建构的方向,这种建构过程又是在什么时候停止的。关联理论认为,关联原则可以对上述问题提供一个比较具体的解决方案。关于关联在认知和交际中的作用,关联理论有两个基本的假设([14,16,18,19]):
(1) 认知关联原则:人们的认知倾向于寻找最大程度的关联性。
(2) 交际关联原则:每一个推理交际的行为都预设了其自身具有最佳关联性。
在关联的认知原则中,关联最大化意味着人类的认知发展会在进化的选择压力下不断地提高认知资源的使用效率,这与人类行为普遍遵循的经济性原则是一致的。作为一种人类认知系统的普遍运行规则,人类的感知机制、回忆机制和推理机制实际上都遵循这条原则,即持续追求认知效果的扩大和处理努力的减少。既然人类的认知系统运作遵循关联最大化原则,那么在人类交际中,说话人只有提供一种对听话人来说具有足够关联性的刺激,才能引起听话人的关注,而这种关注正是成功交际的基础。([16],第185 页)
根据关联理论,交际中一个明示刺激对某人来说是否具有最佳关联,取决于两个条件:首先,该刺激必须具有足够的关联性值得听话人做出处理的努力;其次,该刺激必须是与说话人的能力和偏好相称的最具关联性的选择([18],第256页)。在交际中,说话人基于自己的偏好和能力,选择一个具有最佳关联的明示刺激,听话人接收到该明示刺激后,先假定该明示刺激具有最佳关联,然后通过解码获得词汇意义,并以此为线索,沿着最省力的路径,推断出一个整体性的解释以满足对关联的期待。正是因为说话人用一个隐喻表达的往往是一个相互关联的整体图式,所以在很多情况下难以找到单一的字面表达与之对应,这实际上也体现了语言使用的经济性。([20])这个整体性的解释也就是说话人意图传递的信息。这个推理的过程就是关联引导下的理解启发式:
a.遵循一条最省力的路径来构建出对话的解释(例如消除歧义和不确定指称,调整词汇意义,提供语境假设,推导出蕴含义等等)。
b.一旦达到了说话人所期待的关联程度,推理过程就停止了([16],第185 页)。
2.2 语言隐喻的案例分析
关联引导下的理解启发式是“特设概念”和“关联原则”的组合,可以回答前文提及的触发特设概念建构的对象,沿着哪个方向建构,什么时候停止等等问题。关联理论所提供的解答是:首先,对话语关联的期待,触发了词汇的调整;其次,这种调整沿着一条最省力的路径,都是从最可及的语境假设、最可及的扩大或缩小、最可及的含义开始;再次,通过诸多试探性假设的相互调整,最终形成整体性的解释以满足对关联的期待;最后,当对关联的期待得到满足后,调整的过程就停止了([16],第186 页)。下面,我们将结合具体的隐喻案例,分析关联理论是如何对隐喻的理解做出解释的。
Peter:Is Robert a good accountant?(罗伯特是个好会计吗?)
Mary:Robert is a computer.(罗伯特是一台计算机。)
在上面这个对话中,玛丽没有使用yes(是)或no(不是)来直接回答彼得的提问,而是用了一个隐喻。根据关联理论,当彼得听到这句话的时候,他首先假定这句话具有最佳关联。为了满足对关联的期待,彼得开始沿着最省力的路径对词语“computer”进行解码,形成词汇意义[COMPUTER]。他对[COMPUTER]的相关百科知识条目可能会形成如下假设:
[COMPUTER]:a type of electronic machine;processing large amounts of numerical information well……
(一种电子设备,可以很好地处理大量的数字信息……)
如果玛丽的这句话能够回答彼得的提问,那么彼得对关联的期待就可以得到满足。但[COMPUTER]所激活的假设作为一个整体并不能直接满足听话人对关联的期待。在特定语境下,听话人彼得可能会建构一个特设概念[COMPUTER*]
[COMPUTER*]:a kind of object that can process large amounts of numerical in formation well.(一种可以很好地处理大量数字信息的主体。)
这个特设概念[COMPUTER*]与词汇概念[COMPUTER]相比,百科知识中的“一种电子设备”被抑制了。也就是说,当玛丽说“Robert is a computer”时,她实际上想表达的是:Robert is a[COMPUTER*]。如果彼得理解正确,那么他得到的意思应该是:罗伯特是一个能够很好地处理大量数字信息的会计。上面的对话会激活一个隐含的前提1作为认知语境的一部分。:如果一个会计能够处理大量的数字信息并且不犯错误,那么他就是一个好会计。根据充分条件肯定前件式,彼得就可以推出罗伯特是一个好会计,从而满足了他对关联的期待,对会话含义寻找也就此停止。我们可以用下图1 表示上例中的推理过程。

图1:Robert is a computer 的推理过程
从图1 中我们可以看到,例句的理解有两种不同的可能性:
(1) Robert is a[COMPUTER]:罗伯特是一种能够很好地处理大量数字信息的电子设备。
(2) Robert is a[COMPUTER*]:罗伯特是一种能够很好地处理大量的数字信息的主体,且不是电子设备。
根据关联理论,听话人对关联的期待触发了这两种不同理解的形成,同时也是在关联原则的引导下听话人做出正确的选择。在上述分析中,我们可以看到,语言隐喻的使用涉及到不同的参与者,即说话人和听话人。说话人遵守关联原则,以尽可能小的投入,选择出一个具有最佳关联的语言表达。听话人接收到话语后,首先假定话语具有最佳关联,然后在特定的语境假设中沿着较为省力的路径寻找话语的含义。这不仅包含了解码的过程,同时也包含了推理的过程。当听话人对于关联的期待得到满足时,特定的理解就趋于稳定,对意义的寻找也就停止了。
基于上述分析,我们认为,如果存在一种能够对语言隐喻理解进行整体性的形式刻画工具的话,那么它必须具备如下能力:首先,要能全面涵盖交际所涉及的重要构成要素,如交际活动涉及的说话人和听话人,以及他们之间的互动关系和彼此共享的信息。其次,要兼顾交际中的编码-解码与非论证型推理过程。隐喻语言中的词汇概念,主要以解码的方式提供了相关的百科知识。隐喻表达触发的百科知识并不都是说话人意图表达的内容,因此听话人需要在特定的语境下抑制或剔除某些内容([22])。最后,要反映出关联原则对推理的引导和约束作用。人们出于对关联的期待而启动了推理,同时也因为对关联的期待得到了满足而停止推理。根据关联理论,关联(R)与语境效果(E)成正比,而与认知努力(C)成反比。随之而来的第一个问题是我们怎么测量E和C,第二个问题是对于R的期待是如何在推理中发挥作用的。
我们认为,近年来逐渐兴起的博弈论语用学可以在某种程度上满足上述要求。下文将在介绍信号博弈和IBR 模型的基础上,探讨关联理论所涉及的核心概念是如何在博弈论语用学的分析框架下得以呈现的,并对关联理论有关语言隐喻的分析进行建模和定量分析。
3 信号博弈与IBR 模型分析
博弈论语用学是近年来逐渐发展起来的一种重要的形式语用学分析方法。它以数学和经济学领域中提出的博弈论为基础,旨在建立一种对主体间的交际活动及其规律做出解释和预测的理论。最早将博弈论运用到语言研究的是美国哲学家大卫·路易斯(D.Lewis)。其初衷是为了回答罗素和蒯因等人提出的一个哲学问题:规约性意义从何而来?以语言为例,如果语言是规约的,那么规约语言的语言需要先行规约,对这个“先行规约”又需要规约,一直无穷后退,于是规约变得不可能。相关的论证就会进入一个无休止的循环。为了回答这个问题,路易斯在其著作《规约》([11])一书中运用信号博弈和均衡概念成功地为规约意义的获得提供了一种非循环的解释,同时也为后人使用信号博弈分析人类的交际行为奠定了基础。
一个简单的信号博弈由两个参与者构成,分别是信号发送者和信号接收者。发送者知道自己所处的状态,并发送信号给接收者。由于接收者不能观察到发送者所处的状态,所以他只能根据信号对发送者的状态做出判断。这意味着,发送者拥有私人信息。因此,信号博弈属于不完全信息下的博弈。它可以通过“海萨尼转换”引入一个虚拟的说话人“自然”(Nature),也称为“博弈参与者0”([23]),转变成为一个“完全但不完美信息博弈”。其博弈过程和相关要素可用图2 的如下博弈树表示。

图2:路易斯信号博弈
从图2 中,我们可以看到,一个信号博弈可以分为三个阶段:(1)自然(N)以一定的概率分布P决定发送者S所处的状态t1或t2;(2)发送者根据自己做处的状态选择一个信号m1或m2;(3)接收者R收到信号后,根据这一新信息更新自己对发送者所处状态的信念,并以此为基础做出一个选择a1或a2。图中的虚线表示,当R接收到m1时,他不能确定m1是S在t1状态下发出的,还是在t2状态下发出的。图底端方框内的数字表示接收者根据发送者的信号所做出的不同选择会产生不同的效用值,博弈论中用效用函数对其进行表示。在这个简单的信号博弈中,我们假设接收者如果选对了,那么双方都得到1 单位的收益,否则为0。
路易斯的信号博弈可以表示为一个多元组〈{S,R},T,Pr,M,A,US,UR〉。其中{S,R}表示该博弈由信息的发送者和接收者共同参与;T、M、A分别表示状态集合,信号集合和行动集合;Pr是概率分布函数,确定不同状态的可能性;US,R是效用函数[T×M×A →R],它表示信息发送者和接收者的不同策略组合所产生的效用值。在信号博弈中,信息的发送者需要确定不同状态下的信号发送策略,可表示为一个从T到M的函数:S ∈[T →M]。同样,接收者需要确定收到不同的信号时的应答策略,可表示为一个从M到A的函数:R ∈[M →A]。另外,我们还需要一个函数f为每个特定的情境指派一个交际参与者都希望实现的正确行动。在此基础上,我们就可以确定不同情况下效用函数的值:当Rk(mj)=f(ti)时,Us(ti,Rk(mj))=UR(ti,Rk(mj))=1,否则,就为0。([3],第28 页)。
信号博弈为我们描绘了这样一个较为复杂的交际图景:发送者观察到某个对象,并形成一定的思想或情绪状态,同时他有多个信号可以用来表达。由于信号与思想之间并不是一一对应的关系,所以接收者需要从多个可能的信号中选择出一个他认为是恰当的选项。如果他确定的选项与发送者头脑中希望表达的内容相一致,那么交际就可以成功,并产生一定的交际效果。否则,交际就会失败。
一般来说,一个完整的博弈论分析,不但要提供一个能够涵盖所有重要语境要素的模型,同时还要提供一个解决方案(solution concept)找出说话人和听话人最后会怎么选择([8])。本文的分析主要使用弗兰克(M.Franke)(2009)中的IBR模型([6])。该模型吸收了行为博弈研究中的两个重要发现:其一是主体的推理总是基于某些聚点2“聚点”概念由诺贝尔经济学奖得主托马斯·谢林(T.C.Schelling)率先提出,其基本思想可概括为博弈参与者面对多个选择,在无法通过数理推演找到纳什均衡解的情况下,借助经验、文化和认知等非数理要素共同达到的某一特殊纳什均衡解。([13]),聚点的寻找很大程度上取决于博弈参与者的非论证型推理([20]),其二是主体在推理时会参照参与者类型(player-type)做出最佳反应([4])。它的出发点是一个带意义的信号博弈:〈{S,R},T,Pr,M,[[·]],A,Us,UR〉。其中,〈{S,R},T,Pr,M,A,Us,UR〉是一个标准的信号博弈;[[·]]是一个意义函数,它给定了信号的语义,为主体的推理提供聚点。在此基础上,IBR 模型界定不同层级的参与者及其相应的行动:0-层级的发送者总是根据语义采取信号为真的策略;k+1-层级的接收者对上一层级的发送者策略做出最佳反应。当然,推理过程也可以始于0-层级的接收者。最后,上述推理会进入一个稳定的循环状态。其具体过程可用下图([6],第55 页)表示为:

图3:IBR 推理模式
图3 展示了两条不同的IBR 推理路径。左边这条是从发送者S0开始的,右边这条是从接收者R0开始的。S0总是发送语义上为真的信号,R1针对S0的信号做出最佳反应,S2进而针对R1的最佳反应再做出自己的最佳反应。同样,如果推理是从R0开始的,那么R0首先从字面上理解信号,然后S1针对R0的理解做出最佳反应,以此类推。最后,在某些情况下,发出者和接受者都会在某些行动策略上稳定下来。([6],第58 页)这些稳定下来的策略,实际上就是交际中普遍存在规约。与帕里克(P.Parikh)([12])博弈论模型的求解方案相比,IBR 模型具有明显的优点。它在考虑交际者信念、理性和可能的心理因素的基础上,提供了一种内部的视角,一步步地展示了交际者是如何达到均衡状态的。它可以为解决在线语用推理的均衡选择问题提供一种在认识论上更为清晰的方案,所以也被称为认知博弈论语用学。
基于信号博弈的IBR 模型提供了一个涉及多种重要交际要素的分析框架。首先是交际主体之间的互动关系。信号的发出者根据自己所处的状态发出信号,接收者根据接收到的不同信号做出推理和选择。其次是信号的发出者与接收者共享某些信息。也就是说,博弈的参与者都知道自己处于一个什么样的博弈环境。博弈模型中给出的信息就是博弈参与者所共同享有的。再次接收者需要根据所接收的不同信号做出自己的选择,接收者获取的共享信息越充分,越有可能做出更理性的选择([2],第53 页)。模型中的信号集合M与意义函数[[·]]提供了选择的范围,接收者根据接收到的信号通过推理来修正自己的信念。这与关联理论中的代码-推理交际模型是一致的。最后,选择的过程是在理性选择的驱动下实现的。所谓的理性选择就是主体根据偏好实现效用最大化。这种思想同样也与关联理论的关联概念一脉相承。我们可以运用效用函数为认知效果E和认知努力C提供一种比较意义上的测量。根据关联的计算公式,如果我们假定认知努力C不变,那么我们对关联R的追求,可直接转化为对认知效果E的追求。博弈模型中的效用值反映的就是最终的认知效果E。因此,也就间接地反映了关联R。这样一来,关联理论中难度最大的三个模糊概念,就可以实现必要的量化。
4 语言隐喻的博弈分析
根据IBR 模型([7],第5 页),一个语言使用现象的博弈论语用学分析需要经历如下步骤:首先,确定要分析的话语,并将其作为模型的输入;其次,用信号博弈的基本框架对该话语涉及的重要语境要素进行建模;再次,用IBR 推理描述语言使用过程中说话人和听话人的推理过程;最后,找到模型的输出,即预测到的最佳行为,如果需要可与经验数据相比较,看两者是否相符。
下面我们来看一下上文从关联理论角度分析过的这个对话。在这个案例中,语言隐喻“Robert is a computer”所要传递的会话含义是“罗伯特是一个能够很好地处理大量的数字信息的主体,且他不是电子设备”。如果我们用命题φ表示“罗伯特是一个能够很好地处理大量数字信息的主体”,用命题ψ表示“罗伯特是个电子设备”,那么我们可以在信号博弈的分析框架中区分出两种不同的状态:
•tφ∧ψ:罗伯特是一个能够很好地处理大量数字信息的主体并且他是电子设备。
•tφ∧¬ψ:罗伯特是一个能够很好地处理大量数字信息的主体且他不是电子设备。
不管是在tφ∧ψ还是在tφ∧¬ψ中,说话人都可以使用表达mM:Robert is a computer,说话人还可以使用一个更为精确的表达式mL:Robert is a type of electronic machine which can process large amounts of numerical information well。在一定的语境效应下,我们进一步假定Cost(mM)=0.1,Cost(mL)=0.2。由于隐喻表达是一种松散的话语使用,交际的成功程度取决于听话人所建立的心理表征在多大程度上接近于说话人意图建立的心理表征,因此我们用函数Sim(·)来表示这种相似度。用aφ∧ψ表示:听话人对说话人在tφ∧ψ状态下发出的真信号做出的最佳反应。用aφ∧¬ψ表示:听话人对说话人在tφ∧¬ψ状态下发出的真信号做出的最佳反应。并假定交际的收益Benefit=Sim(tφ∧¬ψ,aφ∧¬ψ)=1,Benefit=Sim(tφ∧¬ψ,aφ∧ψ)=0.3。综合上述考虑,我们可以在信号博弈的框架下对隐喻使用的话语进行建模。

表1 中的“√”号给定了不同信号的语义,即mM在两个状态下都为真,而mL只在tφ∧ψ中为真。基于上述语义,0-层级的发送者发送在不同的状态中均为真的信号,可采取的策略为:
针对0-层级发送者的上述策略,1-层级的接收者需要对其做出最佳反应。首先,需要根据一致性原则计算出当他接收到不同信号后的后验信念(posterior beliefs)。该原则要求信号接收者的后验信念必须与他自己的先验信念和发送者的行为相匹配,这意味着它可以通过如下贝叶斯信念更新公式进行计算:
当他接收到信号mM时,他不能确定发送者的实际类型,因为该信号在两种状态下均为真。根据对话所在的语境,我们假定tφ∧¬ψ的可能性更大,因此可设定P=0.6。根据IBR 模型,R1=BR(µ1)听话人需要根据贝叶斯信念更新公式计算后验信念:
如果1-层级接收者,收到的信号是mL,那么他就可以确定发送者所属的类型是tφ∧ψ,因为发送者只有在状态tφ∧ψ下,才可以发送信号mL。因此,不同信号条件下的后验信念可表示为:

根据上述后验信念,接收者就可以计算自己不同的理解选择所带来的期望效用。当听话人接收到信号mM时,他可以选择aφ∧¬ψ,也可选择aφ∧ψ,但不同选择的期望效用是不一样的。
根据上面的计算,听话人在接收到信号mM后,如果他选择aφ∧¬ψ,那么他得到的期望效用EU ≈0.8。如果选择aφ∧ψ,那么他得到的期望效用EU ≈0.3。因此,出于效用最大化的考虑,他应该选aφ∧¬ψ。同样,当他接收到mL时,也需要计算不同选择的期望效用。但这次相对来说比较简单,因为发送者只有在tφ∧ψ下才能发送mL,所以听话人能够断定说话人在状态tφ∧ψ中。这样,当他接收到mL时,为了获得最大的期望效用,他应该选aφ∧ψ。这样,我们就可以得到R1的策略。
下面来看一下S2的策略选择情况。根据IBR 模型,S2的策略是对R1的最佳反应。当说话人在状态tφ∧ψ下时,他可以发送信号mM,也可以发送信号mL。再考虑到接收者的策略R1,听话人不同的信号选择分别会得到如下效用:
由于在状态tφ∧¬ψ下,说话人只能发送信号mM,所以说话人对R1的最佳反应策略是:
最后,IBR 模型可以预测到:对于所有的K(≥2)-层级的参与者而言,我们都能得到如下相同的策略选择([6],第61 页),这也意味策略的选择达到一种均衡的状态,而这个均衡的状态就是模型的最后输出。
从上面的案例分析中,我们可以看到,博弈论语用学对语言隐喻的形式刻画与关联理论的相关分析具有高度的一致性。在交际的构成要素方面,关联理论认为交际由说话人和听话人构成,博弈论语用学的分析框架中有发送者和接收者。关联理论认为,语言隐喻的理解涉及词汇意义的扩大,听话人需要在Robert is a[COMPUTER]和Robert is a[COMPUTER*]之间做出选择。这种选择在博弈论语用学的分析框架中,就表现为表达式Robert is a computer 可能在两种不同的状态下为真。也就是说,该表达式具有模糊性。关联理论认为,语言交际遵循关联原则,即以尽可能小的认知努力,获得足够多的认知效果。博弈论语用学预设了说话人和听话人都是理性的。所谓理性,指的就是说话人和听话人都要实现自身利益的最大化。这一基本思想与关联原则的核心主张十分相似。上述诸多方面的一致性,也就说明了关联理论有关语言隐喻的分析是可以在博弈论语用学所提供的模型中得到定量分析的。
在用博弈论语用学中的分析中,听话人关于不同状态的先验信念是影响听话人最终做出不同选择的一个重要因素。在上面的分析中,我们假定P=0.6,听话人听到mM后,做出的最佳选择是aφ∧¬ψ。但如果在其他条件都不变的情况下,P的值变成0.2,那么听话人在不同信号条件下的后验信念就可表示为:
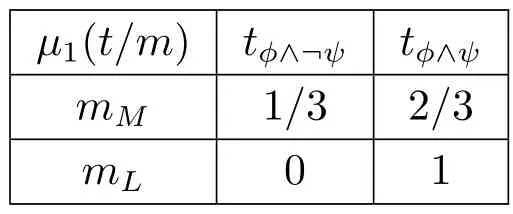
根据上述后验信念,当听话人接收到信号mM时,他可以选择aφ∧¬ψ或选择aφ∧ψ所产生的期望效用就变成:
根据上面的计算结果,听话人在接收到信号mM后,出于期望效用最大化的考虑,他应该选aφ∧ψ。这一结果就与P=0.6 时的选择截然不同。那么,我们就要问,在真实的语言理解中,P值反映的是何种因素,听话人是如何获得P值的。
根据关联理论,词汇概念会激活一组有序的百科知识,这些百科知识在不同的语境下具有不同的可及性,会对话语的关联性产生不同的影响([16],第287页)。在案例“Robert is a computer”中,受该话语所在语境的影响,百科知识条目“能够很好地处理大量的数字信息”的可及性就会被提高,而条目“电子设备”的可及性就会被降低。这里所说的百科知识条目的可及性,实际上反映的就是我们在特定语境下对某些百科知识条目的可能性做出的判断。话语本身和话语所处的语境相互作用,共同决定了某些条目具有更高的可能性。因此,博弈论分析模型中听话人的先验信念和后验信念是一种综合性的反映话语要素和语境要素相互作用的重要指标。可及性是一个具有心理现实性的概念,在关联理论中扮演着十分重要的角色。博弈论语用学的分析框架同样可以将这一重要的概念以概率性信念的方式整合进来。
概率性信念不但可以解释隐喻使用在个体层面上的一些认知问题,而且还可以解释它在群体层面上的交际功能。科恩(T.Cohen)([5],第8 页)曾指出,除了认知和美学功能之外,隐喻还具有增强亲密感的功能。说者通过隐喻发出了一个隐蔽的邀请,听者花费一定的认知努力去接受这个邀请,该行动共同促成了对所属团体的认同。同时,科恩也指出,团体的亲密感不仅来自于听话人能读懂隐喻所含的邀请,而且也来自于他知道不是所有的人都可以读懂这种邀请([5],第9 页)。在日常生活中,隐喻常以一种公开的渠道发布。为什么有些人能很快听懂,但有些人却无法明白呢?科恩认为只有当交际的双方共享一些知识、信念、意图和态度时,隐喻所隐含的邀请才具有可及性([5],第9 页)。我们可以在博弈论语用学的分析框架中重新理解科恩的洞见。由于某些听者与说者共享一些知识、信念、意图和态度,所以他们能够建立比较准确的先验信念,即P 值。而另外一些听者由于缺乏必要的共享知识、信念、意图和态度,所以无法建立准确的先验信念,从而导致理解上的偏差。这也可以进一步解释,为什么隐喻表达可以以公开渠道实现定向传播,发挥出特定的社会功能。
5 结论
关联理论基于特设概念和关联原则等两个重要的概念工具,为语言隐喻的分析提供了一个具有很强解释力的方案。但由于关联理论中存在“互为显明”“非论证型推理”“关联”“认知效果”“认知努力”“认知语境”等概念,使理论解释的形式化存在诸多难以克服的挑战。博弈论语用学中的IBR 模型,在建模时考虑了交际主体的“共享信息”“信号策略”“理性选择”“效用”“概率性信念”等因素,其求解方案采用一种内部视角,一步步地展示了交际者是如何达到稳定的均衡状态(即对表达式意义的正确理解)的。因此,该模型具备了对关联理论进行整体性形式分析的有利条件。本文通过比较发现关联理论与博弈论语用学对语言隐喻的表达分析具有高度一致性,论证了运用博弈论语用学的方法和工具对关联理论的描述性分析进行整体性形式化的可行性。并在此基础上,以IBR 模型为基本工具,根据关联理论对语言隐喻的分析模式,结合具体的案例,系统地展现了影响隐喻使用的各种要素是如何相互作用的,从而形成一种整体性的形式化分析框架,弥补了语言隐喻在形式化分析方面的不足。同时,我们也进一步运用这个整体性的形式化分析框架解释了语言隐喻的发出者是如何利用不同语境中接收者所拥有的概率性信念来实现某些特定的社会功能的。但本文只分析了一种比较典型的语言隐喻,尚未涵盖其他多种类型的语言隐喻。此外,博弈论语用学也是一种自身在不断完善的形式语用学分析方法。因此,我们相信,随着更多博弈模型和求解方法的提出,博弈论语用学可以为隐喻现象提供更好的形式描写。

