维特根斯坦对基本命题的看法的修正
马怿恺
1 基本命题与颜色排斥
在1930 年1 月的头几天里,在与石里克(F.Schlick)和魏斯曼(F.Waismann)的对话中,维特根斯坦对《逻辑哲学论》中关于基本命题的看法做了更多的阐释,或勿宁说是一种修正。([15],第73 页)在《逻辑哲学论》中,维特根斯坦对基本命题做了两个假设:其一是,对命题进行分析就是对复合陈述进行解析,最终达到由对应着简单对象的名称(即简单指号)所直接结合而成的基本命题。([19],简写为TLP,2.0201,2.02,3.2,3.202,4.221)这种分析不必借助于任何逻辑常项,因为逻辑常项并不表象任何东西(TLP,4.0312),诸如“非”“和”“或”“如果”与对象并不相关。其二是,基本命题必须是相互独立的。(TLP,5.134)对于前者(我称之为“分析观点”1本文试图回顾维特根斯坦本人的思考轨迹,在此并不涉足阐释者们有关文本解读路径之间的分歧争论。但值得一提的是,关于维特根斯坦是否确实在《逻辑哲学论》中表达了任何实质性哲学观点,包括“分析观点”是否可以被归结为《逻辑哲学论》中明确提出的实质性哲学教义是有争议的。普鲁普斯(I.Proops)([11])详细讨论了由摩尔记载的维特根斯坦的讲座笔记中的一系列自我批评言论,并对寇纳特(J.Conant)、戴蒙德(C.Diamond)和弗洛伊德(J.Floyd)等人的解读方式提出了异议。),维特根斯坦仍然坚持自己的看法,但对于后者,他认为自己错了。其错误之处在于,逻辑常项的句法规则并非与命题之间的内在结构无关。他谈到的实际例子是,形如“P ∧Q”这样的逻辑积(合取),在被用于谈论同一个点上有两种颜色时,会导致无意义的表达式产生。形式上,如果命题变元P和Q代表相互独立的基本命题,那么就可以对他们进行独立赋值。对P和Q分别进行真值指派会得到四种可能的情况。如果我们对“合取”概念的解释是一个特定的真值函项,并且用《逻辑哲学论》所引入的“T-F符号系统”,即真值表系统(TLP,4.31)来表示这个函项,会如下面这样:
如果P指基本命题A:“x是红色的”,Q指基本命题B:“x是绿色的”,那么“P ∧Q”指合取式A ∧B:“x是红色的且x是绿色的”。根据《逻辑哲学论》6.375 的表述:“正如只有一种必然性是逻辑的必然性,也只有一种不可能性是逻辑的不可能性”。如果上述合取式是假的,那么它就必然是假的,它的必然为假意味着它是逻辑的不可能性。换言之,对于所有的真值可能性,这个合取式都是假的,因而是一个逻辑矛盾。(TLP,4.46)如果把这个逻辑矛盾也用真值表的方式呈现出来,会如下面这样:
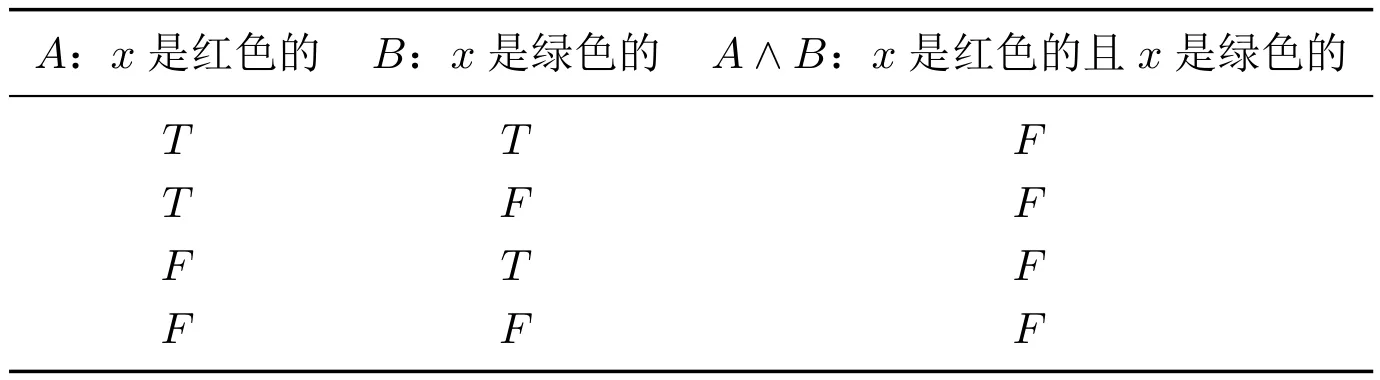
维特根斯坦认为,上面第二张表格是无意义的,因为表格的第一行,TTF,“给予了这个命题的逻辑多样性大于实际可能的逻辑多样性”。([16],第170 页)在《逻辑哲学论》中,所谓逻辑的多样性,就是指用于描绘实在的符号系统与这套系统所描绘的事态之间,恰好有同样多的可能性。(TLP,4.04)通过符号系统能够定义特定概念的所有哲学分析目标是《逻辑哲学论》的重要特点之一,也是“整个逻辑哲学”的任务。(TLP,6.113)正如欣提卡(J.Hintikka)所说的那样:“在这样的分析中,我们必须做的是,为所讨论的概念开发一种符号,使它们之间的所有必要联系成为逻辑真理,最终成为真值函项重言式,可以从我们的纯符号特征的句子中识别。”([5])如果合取式A ∧B为假,那么一方面,其实际的真值情况超出了符号系统原本定义的“合取”函项所具有的所有可能的真值情况;而另一方面,这也与《逻辑哲学论》4.211 的论述相矛盾:“基本命题的一个标志在于没有任何基本命题能与之相矛盾”;反过来,如果合取式A ∧B为真,却又与现实中实在的可能情况(事态)相违背,因而这样的符号表达式并没有能够为实在提供正确的图像。
一种理所当然的辩护会说,“x是红色的”与“x是绿色的”这样的句子根本就不是基本命题。如维特根斯坦自己也说过类似的话:“如果两个命题的逻辑积是一个矛盾式,并且这些命题看起来是基本命题,我们可以看到,在这种情况下,其表象是具有欺骗性的。(比如,A是红色的且A是绿色的。)”2[17],第91 页,8.1.17。安斯康姆(G.E.M.Anscombe)也据此认为“红色”和“绿色”这样的现象语词不能指代简单对象,因而不能是《逻辑哲学论》中的“对象”的例子。参见[1]第25-28 页。但是,《逻辑哲学论》5.557 中也有这样一段话,“逻辑的应用决定了有什么样的基本命题。”既然决定存在什么样的基本命题这个问题是属于经验范围内的问题,那么在我们的日常语境内选择把“x 是红色的”与“x 是绿色的”这样的句子看作是基本命题又有什么不可以呢?
维特根斯坦写作《逻辑哲学论》的初衷之一,是希望“用一种适当的符号系统来表达在普通语言中造成数不尽的误解的东西”。([16],第163 页)如果对基本命题的一切谈论都服务于“把(对任意给定的命题的)分析进行得足够充分”这个最终目标([16],第162 页),同时真值表系统可以被看作是《逻辑哲学论》中所提供的,一种将基本命题的真值可能性符号化的“简单易懂的方式”(TLP,4.31),那么维特根斯坦就必须排除这类符号系统本身,允许产生无意义的逻辑积的可能性。对这种可能性的禁止必须是逻辑上的不可能性,而不能是一种基于经验的不可能性。否则,这就与维特根斯坦自己所说的“逻辑不能与其应用发生冲突。……逻辑与其应用不能彼此重叠”(TLP,5.557)的看法是不一致的。因为,写出特定命题的真值函项表达式,比如A ∧B,属于逻辑的应用范围内的事情,他们只是一般的逻辑形式的替换实例,比如A ∧B是P ∧Q的替换实例。但是,在逻辑中与其应用不重叠也不冲突的部分只能是先验的。(TLP,6.13)通过对逻辑符号做出规定,确定了我们用来描述世界的方法。这是逻辑的基础性工作,必须采取一种不同于物理学的方法。
在《逻辑哲学论》6.3751 中,维特根斯坦曾经提到过同一位置上有两种颜色构成矛盾的例子。他当时类比于物理学上一个粒子不可能同时有两种速度,也就是不可能同时处在两个位置上这个特性,来借此说明同一视野中同一位置不能同时拥有两种颜色,因为“颜色的逻辑结构排除了这种可能性”。
但正如拉姆塞(F.P.Ramsey)在1923 年给《逻辑哲学论》写的书评中所指出的那样:“即便假定物理学家因此提供了一种我们称之为“红”的东西的分析,维特根斯坦先生也只是把困难还原成了空间、时间、物质或者以太的必然属性的那种困难。他明确地使其依赖于一个粒子同时在两个位置的不可能性。”([12],第473 页)基于拉姆塞的批评,我们能够看到,维特根斯坦陷入了一个两难:
一方面,如果诉诸颜色的逻辑结构是对基本命题的补充性阐释,目的在于避免《逻辑哲学论》的符号系统产生出无意义的表达式。那么维特根斯坦实际上被迫承认了,有关颜色的陈述依然具有一定的结构,因而终究还是复合的,且容许被进一步分析的。换言之,逻辑上对基本命题的分析,似乎并没有像维特根斯坦所认为的那样,最终达到了“词项间的终极联结”。那种“不摧毁命题形式本身就不能被打破的直接联结”([16],第162 页),实际在物理上仍然可以被进一步分析,甚至可能必须依赖于物理学上的解释。如果要避免给基本命题找一个物理学的基础,那么维特根斯坦就必须额外再阐明,所有涉及到空间、时间、物质等等属性的情况,何以能够是逻辑上必然的。换言之,“颜色的逻辑结构”在什么意义上是不依赖于物理学解释的结构,需要得到阐明。
另一方面,放弃这种类比的解释效力,意味着维特根斯坦必须连带着放弃《逻辑哲学论》中的一些基本假设,并提供另一种有关于同一位置上有两种颜色构成矛盾的解释。在其唯一于身前公开发表的论文《关于逻辑形式的一些评论》3据肯尼(A.Kenny)报道,这篇文章被维特根斯坦否决了。“不能说它包含了他认为值得保留的任何思想,但它有助于表明他在《逻辑哲学论》完成十年后的思想状态。”([6],第82 页)我想指出,肯尼的后半句没错,但前半句有待商榷。本论文注意到1929 年论文中的部分想法得到了保留,尤其是“命题系统”(Satzsysteme)概念的重要性。尚克(S.Shanker)同样注意到这一点,他认为要理解维特根斯坦在哲学上对哥德尔定理的批评性考察,就必须回到1929 年维特根斯坦的思想转折点。其中“命题系统”的概念第一次被重视,这是维特根斯坦之后在讨论证明概念时所说的“证明系统”(Beweissysteme)的基础。([13],第6-9 页,第122-124 页)中,他将同一位置上有两种颜色的情况从“矛盾”(contradic)替换解释为“排斥”(exclude)([16],第168 页),以此避免将基本命题之间的关系看成是一种逻辑矛盾。在给出这个替换解释的时候,他明确承认了不可分析的陈述(即涉及程度的基本命题)之间存在着一种内在关系,并且引入了一种新的构造来刻画这种内在关系。由此引出了一些新的想法,贯穿着他思想转变的过程。首先最直接的推论就是文章开头所提到的,维特根斯坦在1930 年初便明确放弃了“基本命题必须是相互独立的”这一主张。值得一提的是,放弃这一基本假设并不代表维特根斯坦立刻放弃了命题是实在的图像的构想。到目前为止,离他彻底放弃图像论观点转向对日常语言的语法研究还有很大的距离。正如接下来所要谈到的标尺系统,就其结果而言,这一新的构造只是对真值函项方法下的投影法的一种扩充,因而就其初衷而论,这些新的想法只是对图像论的修正。
2 投影法与标尺系统
在与石里克和魏斯曼的对话中,维特根斯坦重新提到了他在1929 年论文中所谈到的将实在投影到符号系统的投影法。关于投影法的类比论述实际上包含了两层内容:在第一层中,维特根斯坦批评了有关原子命题4在1929 年论文中,维特根斯坦谈到基本命题(elementary propositions)时,采用了罗素(B.Russell)的术语,即原子命题(atomic propositions)。的形式的一种先天的观点;在第二层中,维特根斯坦从正面重新给出了有关原子命题的结构的新想法。具体而言,在第一层中,维特根斯坦把实在的事实比作平面I 中的椭圆形和长方形,把主谓形式和关系形式比作平面II 中的圆形和正方形。两个平面相互平行,通过特定的投影规则实现平面II 对平面I 的描绘,在特定投影规则非常明确的情况下,我们能从平面II 上的图形直接推知平面I 上的精确形状。但如果规则并不是这样明晰,只是大概规定了“平面I 上的椭圆形在平面II 上显现为圆形,并且平面I 上的每个长方形都在平面II 上显现为正方形”([16],第164 页),那么我们就不可能从平面II 推论出平面I 上的精确形状。
同样的类比论述在《哲学评论》和《哲学语法》中得到了重复。维特根斯坦借由投影法的例子,否认了主谓形式本身是逻辑形式,并认为它实际上只是我们的一种记号法。通过主谓形式,我们把数不尽的从根本上有着不同逻辑形式的命题放在了同一种表达方式下。([20],第93 节)而这种困难,在维特根斯坦看来,根植于弗雷格的理论。弗雷格对“概念”与“对象”二词的区分实际上是对主谓形式的普遍化,“概念”就是谓词的普遍化,“对象”就是主词的普遍化,但这么做并不能把握真实的逻辑形式,因为事实上的主谓形式并不是一种单一的逻辑形式。([20],第93 节;[18],第205 页)普通语言的情况就类似于上述投影的例子,我们不可能从对特定语言的规范的使用反推出所描绘现象的真实的逻辑形式,因为我们是“以极多不同的方式将极多不同的逻辑形式都投影到了特定语言的规范中去。”那些看上去都表现为主谓关系的命题,比如“这篇论文是枯燥乏味的”“今天天气是晴朗的”“我是懒惰的”,实际上是彼此大不相同的命题,却被我们归入了相同的逻辑形式中。([16],第165 页)
在第一层中,维特根斯坦认为“原子(命题)形式是不可能被预见的”,因为实在的事实与普通的语言之间的特定的投影规则“并非是根据对先天可能性的推测而来”,而是通过某种意义上后天的研究才能达到正确的分析。([16],第163页)弗雷格的主谓形式是人们对原子命题的结构所作出的其中一种有关先天可能性的推测,但这是语言上的误导。
按照真值函项的构造方式,命题结构是含有变元的函项,要得到一个符合主谓形式的真命题,构成其命题结构的函项只留了一个空位给主目(自变量),因而也就只能赋予这个主目一个值。真值函项处理包含颜色属性的命题时同样如此。假定一个命题断言某个时间T在我们的视野的某个位置P有一种颜色R,缩写为RPT,所有有关颜色的命题都可以这样改写。按真值函项逻辑而言,函项“()PT”只给实在中对应的存在物留了一个空位,这就像“一把椅子上只能坐一个人一样”。([16],第169 页)如果同一时间同一位置有另一种颜色B,那么“RPT并且BPT”就不仅仅是一个假命题,而是一个逻辑矛盾。这似乎意味着基本命题可能会是相互矛盾的,这会导致《逻辑哲学论》的最基本假设失去合理性。为了避免整个计划破产,维特根斯坦修改了措辞,基本命题“虽不可能互相矛盾,但可以互相排斥”。([16],第168 页)这一措辞的修正是十分妥当的,正如上一小节中给出的真值表所示,两个基本命题不能同时为真,但可以同时为假,按现在的说法,即反对关系(contrary relation)。用真值表表示则是:([16],第170 页)

基本命题不可再分析为其他的命题形式(TLP,4.21),如果一定要进一步拆开基本命题看一下内部结构,则只能是名称之间以特定方式结合在一起。(TLP,3.14,3.202,4.22)如果将关于程度的陈述视作基本命题,那么关于程度的陈述也是不能进一步分析成别的命题形式的。维特根斯坦在这里明确主张,程度差异是一种内在关系,因此只能由关于不同程度的陈述之间的一种内在关系来表达。相互排斥的两个命题,比如RPT和BPT,就各自而言都是完全的,并没有留下空位等着被满足后才能成为完全的命题。这样一来,两个基本命题的逻辑积会表现为逻辑矛盾,就被归咎于真值函项的符号系统存在缺陷,因而无法提供实在的正确图像。
真值函项在处理关于程度的陈述时的困难让维特根斯坦看到了问题的关键,即一旦涉及到对实际现象的逻辑分析,“为了表达这些现象,数(有理数和无理数)必须进入原子命题本身的结构之中。”([16],第165 页)维特根斯坦意识到,所有关于程度的陈述“或许存在着一种并不借助于真值函项的逻辑构造”。([20],第76 节)这种构造的可能性意味着我们可以设计出特定的描述系统,即借助数值和等式所构造出的各种不同的“标尺系统”,并把这些系统作为描述有关程度的事实的命题形式。过去,维特根斯坦说过,“它像尺子一样面对实在,只有刻度线的顶端实际触碰了被测量的对象”(TLP,2.1512,2.15121),当时的“它”是指命题,而现在,则是指我们通过构造得到的命题系统。([15],第63 页)
在第二层中,这种构造法的核心特点可以根据维特根斯坦的论述概括如下:([15],第74-76 页)
1)一切命题都是命题系统中的命题;
2)命题系统包含等式和数值;
3)坐标系是一种等式;
4)通过在坐标系中引入数值上的规定,可以实现描述上的多样性;
5)通过对给定坐标系施加特定的句法规则,可以避免同一坐标被规定两次。
维特根斯坦在《哲学评论》第83 节中给出了相关的解释:
“基本命题”这个概念现在已经完全失去了其最初的意义。我通过T-F符号方法所表示的“和”,“或”,“非”等等的规则只是这些词的语法的一部分,而不是全部。
关于描述的独立的坐标概念:比如通过“和”相互联结的命题并不是彼此独立的,他们形成了一幅图像,并且可以检验他们的相容性和不相容性。
尽管我关于将一个有色体置于一个颜色空间之中的那些评论应当使我直接就能得出上述观点,但在我关于基本命题的旧观点(指TLP,3.42)中并没有对坐标值做规定。
实在的坐标只能被规定一次。
相比真值函项的记号法,上述构造法的最大特点就是将数引入了原子命题的形式,维特根斯坦认为这“不仅仅是一种特殊的符号系统的特征,而且也是语言表象的一个本质的因而是不可或缺的特征。”([16],第166 页)在这里,很显然,维特根斯坦并没有放弃图像论的观点,无论是真值函项还是新的构造法,实质上都是投影法。而投影法所刻画的依然是维特根斯坦所说的命题“伸展到实在”的那种方式。即“存在物的形式包含在关于这些存在物的命题的形式之中”。([16],第169页)标尺系统对真值函项系统的挑战,并没有改变维特根斯坦坚持命题与实在之间有着类似于图像之间对应关系的想法。无论是真值函项系统还是标尺系统,都是我们用来描绘存在物的形式的符号化构造,即逻辑形式。不过,仅通过规定逻辑常项的句法形式并不足以决定存在物的逻辑形式,还需要涉及将实在投影到句子的那种投影方式。而真值函项的符号系统的主要问题就在于缺乏对投影方式的刻画,所以新的构造法实质上只是针对这种缺陷给出的替代方案。维特根斯坦承认自己“先前没有注意到逻辑常项的句法只是更综合全面的句法的一部分”([15],第76 页),也就是说,同样是用来将基本命题的真值可能性符号化的句法系统,标尺系统相比真值表系统更加复杂,前者是对后者的一个扩充。他紧接着又说:“但是,也许在命题相互独立的情况下,一切仍然有效——整个推理理论等等”,这意味着,维特根斯坦把形如“P ∧Q”这样的逻辑积的构造,看成是描述系统做了严格限制后的特例情况。如果这个描述系统的句法规则从一开始就保证了同一坐标不会被规定两次,那么在这个完全的系统当中,逻辑积的句法构造仍然是有效的。因此,我们可以说,真值函项系统处理关于程度的陈述时所表现出的不完全性可以通过引入了带有数值规定的坐标系而变成完全的。
3 否定命题与不完全命题
在过去,由于基本命题是相互独立的,所以我们从一个事态的不存在,并不能直接推出其他事态的存在。这样自然会产生一个问题,如果肯定命题表象的是事态的存在,因而赋予了实在多样性,那么否定命题与肯定命题相比是否缺少某些意义?换言之,在《逻辑哲学论》中,我们不能从否定命题推出它的肯定命题,是否意味着在赋予实在多样性方面,二者的地位是不对等的?
现在,在放弃了基本命题必须相互独立的基本假设,同时,确立了关于命题系统的新观念后,下面的陈述实际上就是一条规则:“从一个事态的存在,被这个命题系统所描述的所有的其他的事态的非存在都可以被推出。”([15],第64 页)这条规则能够很好地解释否定命题在赋予实在多样性方面的地位为什么与肯定命题是相同的。维特根斯坦举了一个例子来说明这一点:
如果我说“我没有胃痛”,那么与我说“我有胃痛”时一样,赋予了实在同样多的多样性。因为,如果我说“我有胃痛”,那么,仅仅通过这一命题,我预设了一个肯定命题的存在,我预设了胃痛的可能性,而且,我的命题在胃痛空间中确立了一个位置。并不是好像我目前的状况与胃痛没有一点关系{如果我说:“今天摄氏零度”,那么,据此我已经描绘了温度空间中的零点特征。}如果我说:“我没有胃痛”,那么我可以说,“我处在胃痛空间中的零点”。但是,我的命题预设了整个逻辑空间。([15],第85-86 页)
上述例子中,无论是胃疼,还是摄氏度,都是涉及程度的陈述,并且谈及一个涉及程度的肯定命题就意味着同时预设了三点内容:(1)肯定命题的存在;(2)命题所表象的事态的可能性;(3)与之相关的逻辑空间及在空间中确定的位置。与《逻辑哲学论》中将肯定命题与否定命题对应于同一个可能事态,否定命题必须通过被否定命题才能获得自己的逻辑位置的观点不同。(TLP,4.0641)在命题系统观念下,根据一个命题所预设的逻辑空间,可以给定有关这个命题的一个命题系统。特别地,否定命题所确立的位置可以被解释成这个系统的零点,肯定命题和否定命题各自在系统中确立了一个位置。任何一个命题都是命题系统中命题,肯定命题与相应的否定命题由此处于同一个系统之中。命题的存在性在系统中得到表达,而系统本身则又提供了对实在多样性的表达力。既然二者所处的是相同的系统,那么对实在多样性的表达力也是相同的。正是在上述的意义上,我们可以说,肯定命题与相应的否定命题赋予了实在同样多的多样性。
现在我们来看另一个例子,当要描述一个正方形的特定位置上有一个特定尺寸的圆这个事态时,我们可以通过选择恰当的标尺系统来给出一个有关该事态的完全图像。如果用于指示圆的方位和大小的数量被替换成变元,那么我就得到了一个不完全图像。([15],第39 页)现在,设想这样一个不完全图像:一个红色的圆在一个不同颜色的背景中,背景颜色为x。我们可以在否定的意义上谈论这个不完全图像。
根据罗素的记号法,这句话的否定形式可以表示成,
¬(∃x)φx,读作:并非一个红色的圆在一个不同颜色的背景中;
但同时也可以表示成,
(∃x)¬φx,读作:存在一种颜色x,使得一个红色的圆在这种颜色的背景中不为真。或者换个说法,有一种背景色x,在其之上并没有一个红色的圆。([20],第116-117 页)
维特根斯坦在这里指出的区别,用现在的说法就是否定词的不同辖域,即提前到句首的否定词否定整个句子的真值,句中出现的否定词仅否定某个特定的谓述。但维特根斯坦在这里的论述重点并不只是指出这个区分这么简单。更重要的是要看到第二种形式是无意义的胡话。我们并不能仅通过对否定形式中的命题变元指派一个名称,就实现对它的谈论。比如,要有意义地谈论“圆A不在方块中”,就必须以能够有意义地谈论“圆A在方块中”为前提,仅仅通过给予不在方块中的某圆(变元)一个名称,比如命名为“圆A”是不行的。只有“某个东西在方块中”的意义被确定下来后,谈论“某个东西不在方块中”才有意义。换言之,只有在恰当的命题系统被确定下来后,谈论系统中的对象的否定才成为可能。在上面的例子中,既然红色的圆是以特定的其他颜色为背景的,那么只有当作为背景的颜色通过特定的命题系统被确定下来后,红色的圆才成为这个系统中的对象,并继而能够有意义地谈论这背景上是否有一个红色的圆这样的事态。
上面的例子强调了色斑的逻辑形式预设了整个色斑所属的空间,我们无法脱离这个整体而谈论一部分视觉图像。现在,如果我们把作为背景的部分确定下来,接着谈论其中的视觉图像,比如有这样一句话“在正方形的外部有一个红色的圆”,按照罗素的记号法,即∃xφx,通过存在量词与全称量词之间的转换,它等价于“并非所有红色的圆都在正方形内部”,即¬∀x¬φx。但维特根斯坦不满意这样的记号法转换,他问道:“但是这里的‘所有’指的是什么呢?”([20],第117 页)
维特根斯坦在《逻辑哲学论》中对量词的用法与罗素并没有不同,即把∃xφx看成是一组命题的逻辑和,把∀xφx看作是一组命题的逻辑积([17],第17-18 页,23.10.14;第22-24 页,1.11.14),而且它们并非不适用于无穷论域。([21],第99页,19.8.1919,P.S.(9))但我们实际上永远无法通过枚举来把握住这样的量化,我们借助这样的记号法来谈论普遍化的命题,在1930 年代的维特根斯坦看来是有问题的。([18],第268 页;[10],第297-300 页)还是以“在正方形的外部有一个红色的圆”为例子,这个由存在量词量化的命题,按照罗素的理解,可以写成“或者红色的圆A在正方形的外部,或者红色的圆B在正方形的外部,或者红色的圆C在正方形的外部,……”,但实际情况并不是这样,在这里并没有一个枚举的问题。这里的问题在于,当我们在把一个由存在量词量化的命题拆成一组命题的逻辑和时,实际上是把约束变元替换成了一系列的名称。但正如维特根斯坦所指出的那样,“如果你给予一个东西名称,那么你就不能在同样的意义上给它的颜色、形状、位置和表面起名字。反之亦然”。红色的圆A,红色的圆B,红色的圆C,等等都是名称,但他们仅在某种特定的意义上被归为一类,比如形状和颜色,而在其他方面却是缺省的,比如位置和表面。那么也许实际上红色的圆A和红色的圆B是非常不同的东西,比如A是一个光滑的带有阴影的红色的圆,B是一个粗糙的带有荧光的红色的圆。这意味着包含这些非常不同的对象的命题在以逻辑和的形式被放在一起时,每一个命题都是不完全的图像。同时,由于命名规则总是缺省的,意味着作为析取支的命题数量是无法穷尽的。因而原本由存在量词量化的命题也是不完全的图像。而这一点正是维特根斯坦想要指出的基本命题的一种特性。([15],第38-39 页)
在1929 年的论文中维特根斯坦只是初次谈到命题的完全性与不完全性。他试图通过引入带有数值和等式的命题系统来修补真值函项结构对命题进行分析时留下的不足。这一想法有一个不十分细致的早期版本,那段时间维特根斯坦正在与罗素讨论《逻辑哲学论》的出版事宜,这一想法于那段时间的往来书信中被提及。当罗素就《逻辑哲学论》5.3 的内容提问说:“所有命题都是对基本命题做真值运算的结果吗?那你如何处理一般性?”([21],第97 页,13.8.1919)维特根斯坦在信件附言中简略谈到:“我认为你没有理解我是如何在关于一般性的旧记法中区分其中什么是真值函项,而什么又是纯粹一般性。一个一般的命题是具有某种形式的关于所有命题的一个真值函项。”([21],第99 页,19.8.1919,P.S.(8))在这里我不对真值运算做展开,这会引出超出本文限度的讨论。5维特根斯坦在《逻辑哲学论》中进一步发明了一种被称为“N 算子”的记号法,并尝试揭示出全称量化与合取式、存在量化与析取式之间的内在关系,继而在不借助量词逻辑的情况下构造出量化语句,并基于这类运算来刻画一般性。吉奇(P.T.Geach)([4])和弗格林(R.J.Fogelin)([3])对这一技术分别进行过详细的解读、修正,对二者的解读与彼此间争论的回顾可以参考兰迪尼(G.Landini)。([8])兰迪尼认为维特根斯坦实际上未能实现自己在技术开发方面的想法,逻辑哲学论中所设想的“N 算子“只是假设存在着满足这种技术要求的构造物,而这种信心恰恰来源于对逻辑的可判定性的信念。维特根斯坦在此后并没有对这一技术想法做更多的努力,而是把对可判定性问题的调查全部留给了拉姆塞。但这里对一般性所做的区分却是显然重要的。因为它表明了,在《逻辑哲学论》已然成书时6根据[21],第89 页,13.3.1919 中维特根斯坦对罗素所言,《逻辑哲学论》于1918 年8 月完稿。讨论TLP,5.3的书信往来则发生在1919 年8 月。前后时隔一年。,维特根斯坦便已经确信,能够真正作为命题的一般形式的东西并非真值函项这么简单。这种想法在《哲学评论》中得到了充分的阐释。([20],第115-122 页)维特根斯坦将“我看见红色的背景中有一个圆”这样的一般性的句子视为对可能性留有开放性的命题,并把这样的命题看作是不完全图像,就像没有画上眼睛的肖像画。这种看法在魏斯曼的笔记中也得到了印证,维特根斯坦有如下表述:
命题“在正方形中有一个黑色的圆”除了包含“正方形”、“黑色”“圆”“在……之中”以外不包含任何东西。这就是全部了。命题所言说的内容不能超过它所包含的内容,而我们能够理解它这一事实显示出,即使它有着不完全的形式,它也是一个命题。一个不完全的图像必须显示它是不完全的。必须有可能从一个命题中推测出仅仅是一个事态的不完全的肖像。这样的命题必须显示它周围的一切东西在某种程度上依然是开放的。它必须显示它的开放性。一个基本命题描绘了空间中所有的颜色。([15],第41 页)
在“不完全的”这里存有一处脚注,其中魏斯曼记录了维特根斯坦的一个形象的举例,即哪怕一个人完全描述了某个房间内的全部东西,这依然是一个不完全图像。因为我们总可以谈论房间的外面有什么。这意味着,我们必须能够从相关命题中看到它并不能描绘所有的东西这一点。而这正是命题所具有的开放性。这种开放的可能性是我们将命题应用于描绘实在时必然会产生的。而且这种开放的可能性意味着“越一般的,也就是越不完全的描述,相比越完全的描述来说,越有可能与事实相符。”7[20],第115 页。此时的维特根斯坦还把基本命题的不完全性视为概率理论的重要特点,这与《逻辑哲学论》5.1 形成了强烈的对比:“所有的真值函项可以被排成序列。这就是概率理论的基础。”
在这里,维特根斯坦调转了命题与命题的一般形式之间的派生关系,甚至调转了一般性概念的含义。在《逻辑哲学论》中,我们通过真值函项结构给出了关于所有命题的一般形式,并把这个一般形式本身就视作是一般性概念,即构造命题的统一方式。(TLP,6)所有基本命题都是他们自身的真值函项,且所有基本命题的真值函项都是以基本命题为基础施以诸真值运算的结果,而所有的命题又是对诸基本命题施以诸真值运算的结果。(TLP,5,5.234,5.3)粗略来说,早期的维特根斯坦认为,命题是从命题的一般形式中派生的。而在1930 年代初的维特根斯坦看来,一般性是借助不完全图像对实在的描绘而“进入到基本命题的原理之中的”([20],第115 页,下同),不完全图像的对错“取决于实在是否与从这幅图像中读出的东西是一致的”。结合前述引文([15],第41 页),某种意义上可以说,事物的存在方式就是由所有不完全的命题结合在一起形成一个完全的基本命题。当我们谈及对象的整体时,“必然存在着不完全的基本命题从其应用中得以派生出一般性概念”。至此,维特根斯坦更新后的观点已经十分显然了,命题的一般形式才是从作为不完全图像的不完全命题中派生的,而不是反过来。如果说之前被视作一般形式本身的一般性概念是先天的,那么更新后的理解则把一般性概念视为是从对基本命题的应用中派生的,因而是经验的,也是后天的。更重要的是,维特根斯坦在这里大手笔地改变了他对基本命题的看法,他承认存在着“不完全的基本命题”,这种基本命题显然不再适用于为事态的存在和不存在的各种可能情况提供解释模型。(对比TLP,4.3)这意味着此时的维特根斯坦已经决定将真值函项结构抛诸脑后,转而寻求一种新的语言分析方法。
4 “现象学”与分析观点的改变
我们可以看到,颜色排斥问题是维特根斯坦试图修正《逻辑哲学论》基本假设的起点。维特根斯坦放弃了《逻辑哲学论》6.3751 中的物理学类比论证,转而寻求有关颜色排斥的新解释。为了解释涉及程度的命题如何作为实在的图像,他转而通过命题系统来呈现系统中的命题之间的那种内在关系,以此来取代过去对一切命题做真值函项结构的分析。命题系统的想法是全新的,至少有如下推论:(1)所有命题都预设了自身所处的逻辑空间,在命题系统内的基本命题也是相互关联的,因而不再是相互独立的;(2)并且基本命题不再必然是肯定命题了,因为基于命题系统,否定命题与肯定命题在赋予实在多样性方面有着相同的地位;(3)在命题系统内,缺省某些描述的命题,即带有变元的命题是不完全图像,不完全图像对实在的描绘具有开放的可能性,因而一般性概念是从作为不完全图像的不完全命题的应用中派生出来的;(4)在命题系统内,不完全的命题也可以是基本命题。这些推论从表面上看已经拆毁了《逻辑哲学论》的基本假设,但反过来说,这确实是对《逻辑哲学论》实打实的修正。《逻辑哲学论》5.156 中有一处括弧,维特根斯坦说了一句看起来有些悖谬的话:
一个命题虽然可能是某一事态的一个不完全的图像,但是它总是一个完全的图像。8另见[17],第61 页,16.6.15,其中维特根斯坦的德文原文对“总是”用了大写强调,对“一个完全图像”用了斜体强调。皮尔斯(D.F.Pears)与麦金尼斯(B.F.McGuinness)的译本在这里把“一个完全图像”翻译为“关于某种东西的一个完全图像”,并把强调加在“某种东西”(something)上,减轻了悖谬感。但本文为了讨论这种悖谬感,故采取TLP 5.156 德语本身对“ein”的强调。本文下述同段引文皆出自此处。在早期思想中,一个命题要有意义,其句法成份的各个部分的意义都必须确定下来,一个命题分析到最后必须有一个终点,这个终点就是他所说的简单指号,即名称。他把如上述那样确定了意义的命题视为完全的图像。虽然当时的他也承认“还存在着它(命题)没有说的东西”,但是既然命题“对所说的东西是完全加以言说的”,那么“那些还没有说到的东西就压根不能属于其意义”。很显然,说命题是完全的图像的根本理由是因为对命题的分析总有一个终点。而对命题的分析之所以有一个终点是由名称的实指存在性保证的。作为完全图像的命题又是由确定了意义的名称直接组合而成的。9沙利文(P.M.Sullivan)([14])认为早期维特根斯坦在“分析观点”上存在某种张力:在致力于将日常命题分析为基本命题的真值函项的复合物的计划的同时,却完全不知道在特定情况下这种分析究竟是如何进行的。似乎仅仅是独断地假设了逻辑原则可以被应用于日常命题,且其中出现的表达式最终会是简单的。沙利文围绕简单性概念提供了一些新颖的解读,他认为维特根斯坦实际上是在处理命题的“隐蔽的复杂性”时面临着某种认识论上的困难。因而维特根斯坦才会试图对“分析”能够为命题推理提供有效性这一承诺做出进一步解释。在沙利文的这种解读下,维特根斯坦实际上在《逻辑哲学论》中并没有放弃而是采纳了1915 年在笔记中所考察的简单性概念。如果这样的解释已经足以回答“分析观点”所遭遇的困难,那么是否还有必要在《逻辑哲学论》中坚持基本命题在逻辑上是相互独立的这一要求似乎会是一个尖锐的问题。弗洛伊德([2])对沙利文的这一解释做了一些回应,她赞同克雷默(M.Kremer)([7])的看法,即否认维特根斯坦以任何方式直接关注了“有效性的理论特征”(the theoretical characterizations of validity),相对地,他所关注的是“特定推理的正当性”(the justification of particular inferences)这虽然看起来是一个完美的闭环,但这个闭环也以独断的方式回避了那些命题还没有说的东西究竟要怎么处理。颜色排斥问题让维特根斯坦看到了不完全图像之间的相关性,曾经他所以为的能够区分命题所说与未说的那种“清晰的定义”(SHARPdefinition)([17],第61 页,16.6.15)并没有那么容易得到。相反,具有开放性的不完全图像似乎更符合事实实际的样子。于是,我们也可以认为维特根斯坦是把过去“总是一个完全的图像”的命题放置到更具多样性的命题系统中去看待。上述看似悖谬的话也可以改写成:“一个命题虽然可能是某一事态的一个完全的图像,但从命题系统的视角看,它不必总是完全的图像。”
如果我的解读是有道理的,那么维特根斯坦对不完全图像的接纳与鞠实儿对涉及开放谓词的命题语句的关注有许多相似之处。鞠实儿认为弗雷格-卡尔纳普传统所给出的经典逻辑的语义理论承诺了某种外延主义教条,即“某个体具有某性质等价于它属于某集合”([22],第18 页),由于概念词的内涵需要通过谓词的语义解释来表达,而在经典逻辑中,概念词的外延被限制在固定的论域下,这就使得相应的谓词的语义解释也总是一个封闭类。但若从日常生活的知识表达需求出发,我们“总是在已有的背景知识下描述新个体”([22],第28 页),“当新个体不满足某谓词时,它必满足另一个谓词,这两个谓词所表达的性质互不相容”。([22],第9 页)比如前文所举的例子中,由于A是一个光滑的带有阴影的红色的圆,而B是一个粗糙的带有荧光的红色的圆,那么实际上红色的圆B相对于红色的圆A是一个新类型的个体。“红色的圆”这个复合概念词在经典逻辑下是以封闭类的方式进行形式化处理的,那些要么不相容的性质差异在形式化过程中被抽象掉,要么简单地用两个不同的个体词项去指称具有不相容性质的个体,前者在知识论层面粗暴地做了削减,后者则在本体论层面简单地增设了实体。
这里的洞见有助于我们看到维特根斯坦思想中某种关键性的注意力变化。在1929 年之前,维特根斯坦并不关心知识论问题,在《逻辑哲学论》中他说:“知识论是心理学的哲学”(TLP,4.1121),他认为自己是一个“逻辑学家”,那些属于自然科学或者逻辑的应用(TLP,5.557)的内容他并不关心,因为这些在他看来是“纯粹经验性的事情”。([9],第70 页)而到了1929 年以后,维特根斯坦开始意识到有必要将知识论相关的内容纳入到他关于逻辑的追问中,所以他说:“现在我们只有通过检查我们想要描述的现象才能用清晰的符号法来代替不精确的,从而试图理解它们的逻辑多样性。也就是说,我们只有通过对现象本身的逻辑研究才能得出正确的分析([16],第163 页,我自己加的强调),也就是某种意义上后天的(a posteriori),而不是通过猜测其先天的(a priori)可能性”。([16],第163 页)他甚至曾设想过某种有关颜色的现象学理论,通过将简单颜色视为简单的心理学现象来进行研究。这种理论必须不同于物理学和生理学,它仅涉及那些实际上可感知的东西,却没有任何自然科学所假设的对象,他称其为纯粹的(pure)现象学。([20],第273 页)这种设想在与魏斯曼和石里克的谈话中也有印证。他认为他所说的“现象学”的最大特点在于,这是一门关心“可能性问题”或者“意义问题”的学科。其目的是给出“事态结构的描述”,而不是像物理学那样出于“确定事物的规律性”的目的而只关心“真假问题”,“其余的都不关心”。([15],第63页)我认为,维特根斯坦这一注意力的转移标志着他对“分析观点”的理解发生了方法论意义上的转变。较早的“分析观点”完全服务于逻辑的基础性研究,短暂的“现象学”意义上的“分析”松动了这种观念。随后不久,维特根斯坦就转向了对具体现象的细致调查,并注意到日常语言本身的重要性。这促使他转而投入到语法分析的工作中,并为日后他在《哲学研究》中再度与《逻辑哲学论》的思想正面对峙做了准备。

