多种方法求面积
杨 海
(新疆维吾尔自治区哈密市伊州区陶家宫镇中心小学)
小朋友,在计算图形的面积时,规则图形可直接用公式算出面积,遇到无法直接用公式计算的图形时,可以运用分割、平移、旋转、拼补等方法将图形进行转化,再用面积公式计算出所求图形的面积。
分割法:将原图形分成若干个规则的图形。
例题1图1是一座房子地基的示意图(单位:米),这座房子的占地面积是多少?

图1
可以将图1分割成一个正方形和一个长方形(如图2),正方形的面积是10×10=100(平方米)。长方形的长是20+10=30(米),宽是20-10=10(米),面积是30×10=300(平方米)。这座房子的占地面积是100+300=400(平方米)。

图2
例题2如图3所示(单位:米),有一个正方形的花坛,在花坛的四周铺上4米宽的草坪,草坪的占地面积是192平方米。花坛的占地面积是多少?
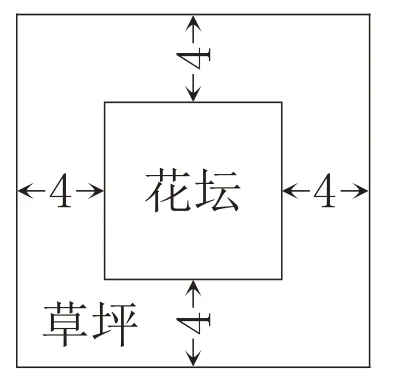
图3
解答这道题的关键是算出花坛的边长,可以将草坪分成4个同样大的长方形(如图4),因为草坪的面积是192 平方米,所以一个长方形的面积是192÷4=48(平方米)。已知草坪的宽是4 米,可算出一个长方形的长是48÷4=12(米)。花坛的边长是12-4=8(米),面积是8×8=64(平方米)。
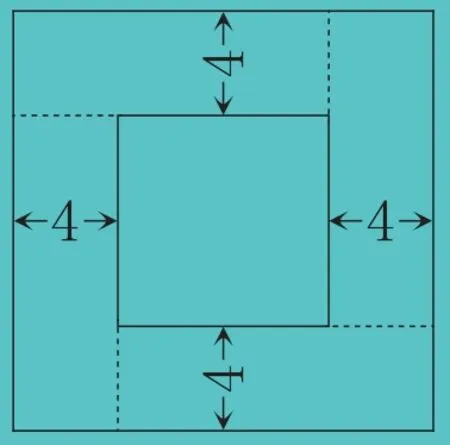
图4
补形法:通过添加辅助线,把不规则图形补成规则图形。
例题3如图5所示(单位:米),王爷爷开垦了一块形状不规则的菜地。你能算出菜地的面积吗?

图5
通过添加辅助线,把图5补成三角形。如图6所示,三角形的底是20+5=25(米),高是20+6=26(米),面积是25×26÷2=325(平方米),后补的长方形的面积是5×6=30(平方米)。菜地的面积是325-30=295(平方米)。

图6
割补法:把不规则图形的某一部分割下来,补在图形的其他位置,使其转化为规则的图形。
例题4图7中A、B两个正方形的边长和是18厘米,A的面积比B大36平方厘米,求B的面积。
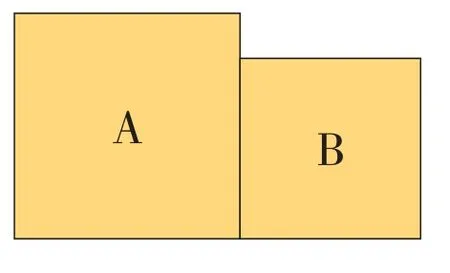
图7
如图8所示,从A 中挖掉和B 一样大的正方形C,A中剩下的D、E、F三部分的面积和是36平方厘米,把F割下,拼到B的上方,这样D、E、F 三部分就拼成了一个长是18 厘米、面积是36 平方厘米的长方形,这个长方形的宽是36÷18=2(厘米),这个宽是正方形A、B 的边长之差,又已知A、B的边长之和是18,根据和差问题的解法可求出B的边长是(18-2)÷2=8(厘米),B的面积是8×8=64(平方厘米)。

图8
等面积变形:把原图形转化成另外一个图形,形状变了,面积不变。
例题5如图9所示(单位:厘米),一个长方形的草坪中有一条宽2 米的小路,小路的占地面积是多少?

图9
小路是不规则图形,把小路分成若干小段,每一小段分别向下或向右平移(如图10)。大长方形的面积是30×20=600(平方米),小长方形的面积是(30-2)×(20-2)=504(平方米)。小路的占地面积是600-504=96(平方米)。
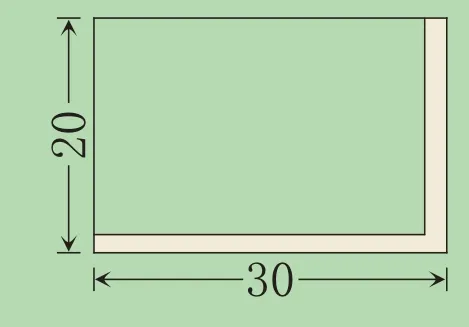
图10
例题6如图11所示(单位:厘米),你能算出阴影部分的面积吗?
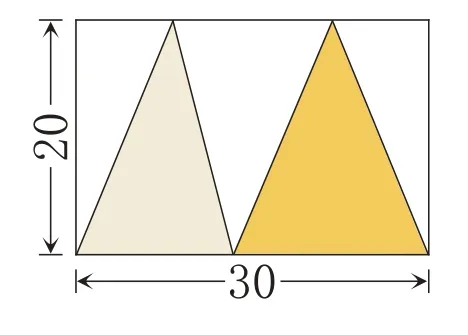
图11
图11中的两个三角形的高相同,都是20厘米,但是不知道两个三角形的底,无法直接用三角形面积公式计算。
先观察图12,你会发现三角形ABC、三角形DBC、三角形EBC的底是都是BC,高相等,都等于长方形的宽,所以这3 个三角形的面积相等,根据这个方法,可以把图11转换成图13。阴影部分的面积是30×20÷2=300(平方厘米)。

图12

图13
小朋友,你学会了吗?求面积的方法还有很多,你在平时的学习中一定要善于总结,积累更多的方法。

