自动驾驶车辆侧向路径跟随控制算法仿真

徐 浩

（长安大学 汽车学院，陕西 西安 710064）

自动驾驶系统已经成为当前汽车研究热点，其中智能车辆的路径跟随控制应用广泛，比如应用车辆纵向控制的自适应巡航控制系统（Adaptive Cruise Control, ACC）、汽车主动安全系统（Autonomous Emergency Braking, AEB）、车道保持系统（Lanes Keep Assistant System, LKAS）以及主动避障技术涉及到车辆的侧向控制等。最优预瞄理论[1]是根据驾驶员在实际驾驶过程中对前方道路信息的预估，为减小行驶轨迹与期望轨迹偏差，建立预瞄误差和方向盘转角的传递函数，得到最优方向盘转角输出。跟踪控制的最基本要求是提高路径跟踪精度，为减小跟踪偏差并考虑对输入输出进行约束，模型预测控制理论被应用到路径跟踪研究中。模型预测控制器也叫做滚动时域控制器[2]，该控制器根据被控系统当前的状态量对未来控制时域内的状态量预测，通过迭代最终得到控制变量函数，并且针对系统中各执行器的特性进行约束，使得系统在未来一段时间内的跟踪误差最小，从而得到最优的控制输入。

为实现自动驾驶车辆跟踪轨迹的横向控制，本文采用基于预瞄误差模型的模型预测控制，基于动力学以及对车辆参数的合理简化，建立二自由度自行车模型，根据车辆位置信息、状态量和预瞄点以及期望轨迹建立预瞄误差模型，以上作为模型预测侧向控制器的输入，并对输入输出进行约束，对目标函数求解，最终实现轨迹跟随控制。

1 系统模型

1.1 车辆模型

在侧向路径跟踪工况下，本文建立具有侧向和横摆运动的二自由度自行车模型，如图1所示。根据车辆动力学以及牛顿第二定律[3]，车辆在质心处Y轴和绕Z轴的动力学平衡方程为

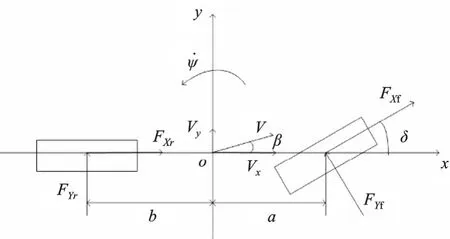
图1 车辆二自由度模型

车辆模型沿Y轴的合力和绕Z轴方向的合力矩分别为

式中，a,b为质心距前后轴的大小；FYf和FYr分别为前、后轮胎与地面的侧偏力；δ为前轮转角。

轮胎的侧偏角与侧偏刚度处于线性侧偏特性下且δ较小，式（2）可以表示为

式中，Cαf，Cαr分别为前后轮的等效侧偏刚度；αf，αr分别为前后轮的侧偏角。

根据车辆模型假设[4]，质心侧偏角β较小，前后轮侧偏角由式（4）求得

综合以上各式得到车辆动力学模型为

1.2 预瞄跟踪误差模型

如图2所示，建立车辆行驶路径与期望的道路路径之间的误差关系，ed为选取的目标点与目标道路的预瞄点P的横向距离误差；L为车辆与前方目标点的距离；O点为车辆质心位置坐标。

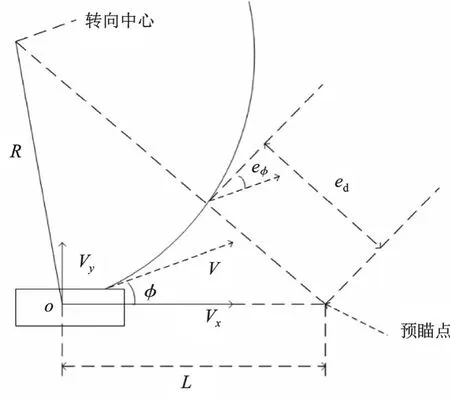
图2 路径跟踪误差模型

从图2几何关系可得车辆与目标路径的距离误差和航向偏差：

1.4 组培苗的生根培养 将外植体上分化出的不定芽剪切下来，转到MS基本培养基上培养。待组培苗生长到5～6 cm，并且长出2到3片幼叶时，将其分别转到0、0.1、0.2 mg/L NAA浓度的生根培养基中，促不定根萌发。30 d后取出与CK(0 mg/L)进行比较，筛选出合适的NAA浓度，用于诱导生根。

期望的车辆航向角变化率可根据式（7）计算得[5]

式中，ρ为参考路径曲率。

当质心侧偏角和航向角偏差很小，跟踪误差模型可用式（8）表示：

式中，

2 MPC侧向跟踪控制器

2.1 模型离散化

采取向前欧拉法的方式，设时域为TS，对上述连续方程离散化，得到离散形式：

2.2 目标函数设计

路径跟随控制器控制过程的目的为使输出量Y(k)最小，此外，控制过程中前轮转角也应受到限制。设计目标函数如式（11）所示：

式中，Q,R为输出量Y(k)和控制量的权重系数。

2.3 约束条件建立

约束条件是指将车辆的前轮转角限制在合理范围，如式（12）所示：

文献[6]中，为了保障安全性和舒适性，设置前轮转角最大值δfmax=0.436 rad。

侧偏角不超过5°时，侧偏力与侧偏角呈线性关系，故设置轮胎侧偏角的约束为

2.4 二次规划问题求解

式中，

将目标函数转化为二次型形式，并结合约束条件进行求解。

在当前控制周期内完成对式（15）的求解后，得到时域内的控制输入量序列U×(t)，将该序列的第一个元素作为实际的控制量。

3 仿真验证

应用CarSim-Simulink联仿平台验证侧向路径跟踪控制器的跟踪效果，选择CarSim软件中的C级汽车进行仿真，具体车辆信息以及仿真参数如表1所示。

表1 仿真参数

应用五次多项式规划换道路径，起始点坐标为[0,0]，终点坐标为[20,10]，曲率都为0。仿真时间20 s，仿真结果如图3—图5所示。从图3—图5可以看出，前轮转角没有超过0.463 rad在约束范围内输出，得到的实际路径与期望路径也基本一致，轨迹跟踪效果良好，横向误差在0.3 m内，横向误差较小。

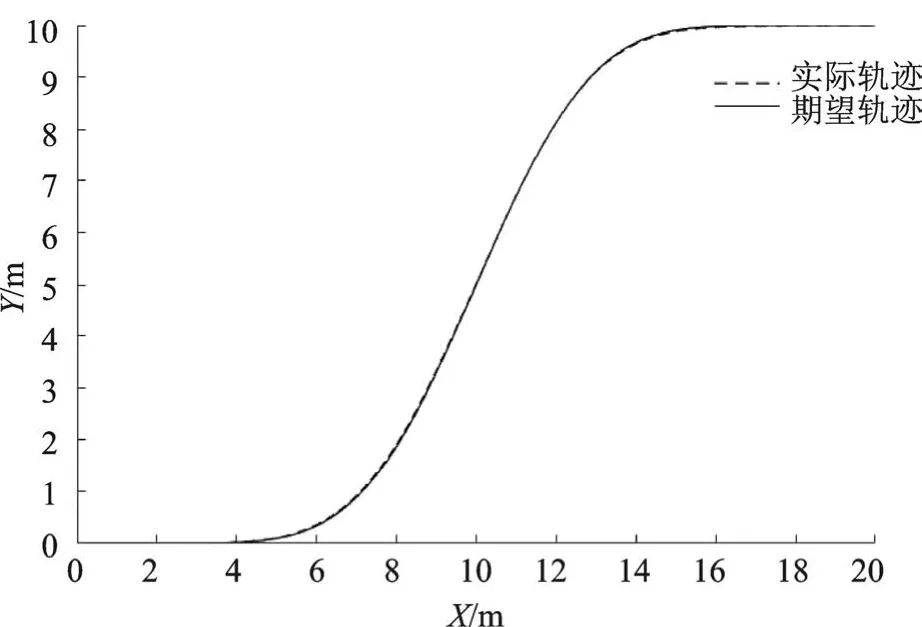
图3 轨迹跟踪

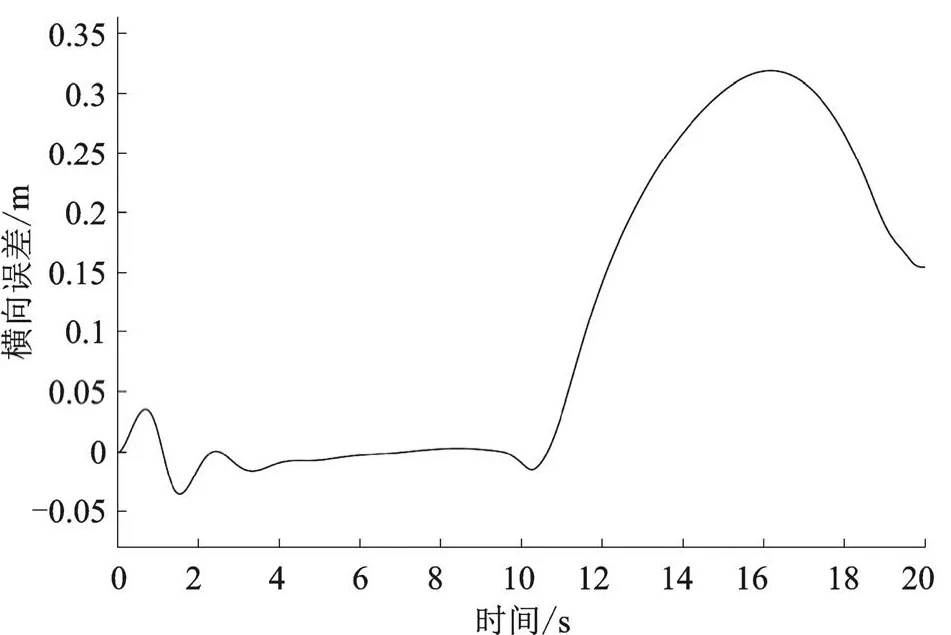
图4 横向误差

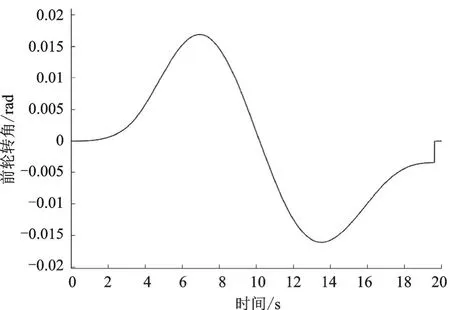
图5 前轮转角

4 结语

本文根据车辆动力学建立二自由度车辆模型，为减小横向跟踪误差，结合预瞄误差模型基于模型预测设计横向路径跟随控制器，在CarSim-MATLAB平台下进行仿真，结果表明该控制器对路径跟随效果良好，输出量前轮转角也在合理约束范围内。