城市峡谷环境多源导航信息弹性融合定位方法

孟 骞,姜颖颖,王立辉,胡祎雯,李圣英

（1.东南大学仪器科学与工程学院,南京 210096;2.东南大学微惯性仪表与先进导航技术教育部重点实验室,南京 210096）

0 引言

现代都市环境下,道路交通周边高楼林立且拥挤,形成类似自然峡谷的城市峡谷环境。在城市峡谷场景中,卫星导航信号（Global Navigation Satellite Systems,GNSS）易受到建筑物遮挡和折射,惯性导航系统（Inertial Navigation System,INS）的误差容易随时间积累,以视觉以及激光雷达LiDAR等新兴传感器为代表的SLAM（Simultaneous Localization and Mapping） 技术对环境和天气较为敏感[1]。在城市峡谷环境下单一传感器一方面暴露出脆弱性和局限性,另一方面突出表现为以故障、偏差为典型现象的模型失配,无法满足生命安全应用需求对定位精度、完好性、连续性等的要求[2]。

弹性PNT（Resilient Positioning,Navigation and Timing,Resilient PNT）是近些年来受到较多关注的新兴PNT 服务模式。弹性PNT 强调的是以多源PNT 传感器优化集成为平台,以函数模型弹性调整和随机模型弹性优化为手段,融合生成适应多种复杂环境的PNT 信息,以提高海、陆、空、天等各领域关键任务应用的可靠性和安全性[3]。弹性导航理论的先进性从物理属性上不仅表现为可以确保物体在多种外力作用下通过消解抵抗化解外力影响且保持自身完好,而且也表现为功能上可适应于多种外部环境的灵活适应能力[4]。2020年,美国国土安全部科学技术局发布《弹性PNT 合规性框架报告》,定义了弹性PNT 应具备的预防、响应和恢复三大功能以及面向最终用户需求的四个级别及其对应要求[5]。早在2018年,杨元喜院士[6]已撰文阐述弹性PNT 的基本框架,在用户终端层面提出实时或准实时地修改、选择已有观测模型,使其适应相应场景和相应传感器的“弹性函数模型” 的概念以及随观测信息不确定度而弹性变化的“弹性随机模型” 的优化策略。美国空军理工学院的Jurado 等[7]研究了一套面向多传感器全源导航的在线弹性自主管理系统（Autonomous and Resilient Management of All-source Sensors,ARMAS）,系统架构由监测、验证、标定以及模型重构等多项功能闭环完成。美国加州大学欧文分校的Kassas 团队[8]利用机会信号开发无线电SLAM 技术,实现了卫星拒止环境下的弹性导航。韩国船舶与海洋工程研究所[9]设计了基于增强罗兰设备的船舶弹性PNT 系统以应对GNSS 信号弱易受干扰的问题。美国Geodetics 公司[10]基于小型化SWaP-C系统搭建了集成GPS/IMU/保持振荡器/视觉多传感器的终端,通过冗余IMU 和分布式网络等提高了拒止场景下的定位精度和连续性。针对GNSS 和视觉应用均具有挑战性的城市峡谷自动驾驶场景,2021年加拿大女王大学的Noureldin 团队[11]将自适应巡航系统调频连续波雷达、简化惯性传感器、磁强计与传统GNSS 进行整合,建立了基于快速正交搜索非线性误差模型的多级组合导航系统,同时在2022年进一步建立了惯导与GNSS 精密单点定位技术（Precise Point Positioning,PPP）的紧组合模型,可以在GNSS 信号中断情况下实现车道级连续导航[12]。国内学者在弹性PNT 的架构设计方面也有探索性成果,武汉大学的刘万科等[13]针对室内外切换定位挑战提出了一种基于云-端协同增强的多类传感器集成、多种先进技术融合的多体制协同精密定位架构,在智能手机平台实现了云-端协同和多源协同。空军工程大学的张伟等[14]以定位精度为效用函数,研究了基于博弈论的PNT 手段选择策略,属于多传感器弹性优选方面的探索。当前,针对弹性融合的终端架构模型构建方面,还处于需求量化、功能定义和新兴技术探索阶段,迫切需要提出和验证更先进的架构解析模型和拓扑模型,以拓展弹性融合理论的科学范畴。

城市峡谷环境是弹性PNT 技术的典型应用场景,弹性导航理论为解决城市峡谷环境下的自主导航问题提供了新的思路。本文面向城市峡谷环境下的多源信息融合导航应用,提出了一种基于观测传感器独立更新的弹性融合方法。主要架构特点是各观测传感器保持独立运行,对系统状态的更新也独立完成,从而降低不同传感器之间的耦合度。同时在保证最优估计的前提下,尽可能将数据融合功能往终端状态输出层面下沉,并采用两级交互式架构。首先得到各通道的后验模型概率,进一步计算以后验概率为权值,得到数据融合输出,最后采用典型城市峡谷场景下的实际动态实验数据对方法的优越性进行了验证。

1 多传感器弹性融合算法概述

本节将介绍基于传感器独立更新的交互式弹性融合算法的功能实现架构,其示意图如图1所示。在每一个导航历元,导航系统在状态预测与传播后,一步预测的状态分别送给各观测导航源进行独立更新,整个过程并行处理,各独立导航源的信号通道之间没有相关性和状态耦合。同时引入观测传感器的先验置信度,以马尔科夫链的形式用于状态交互式弹性融合以及各通道的状态初始化。相关具体算法推导如下:

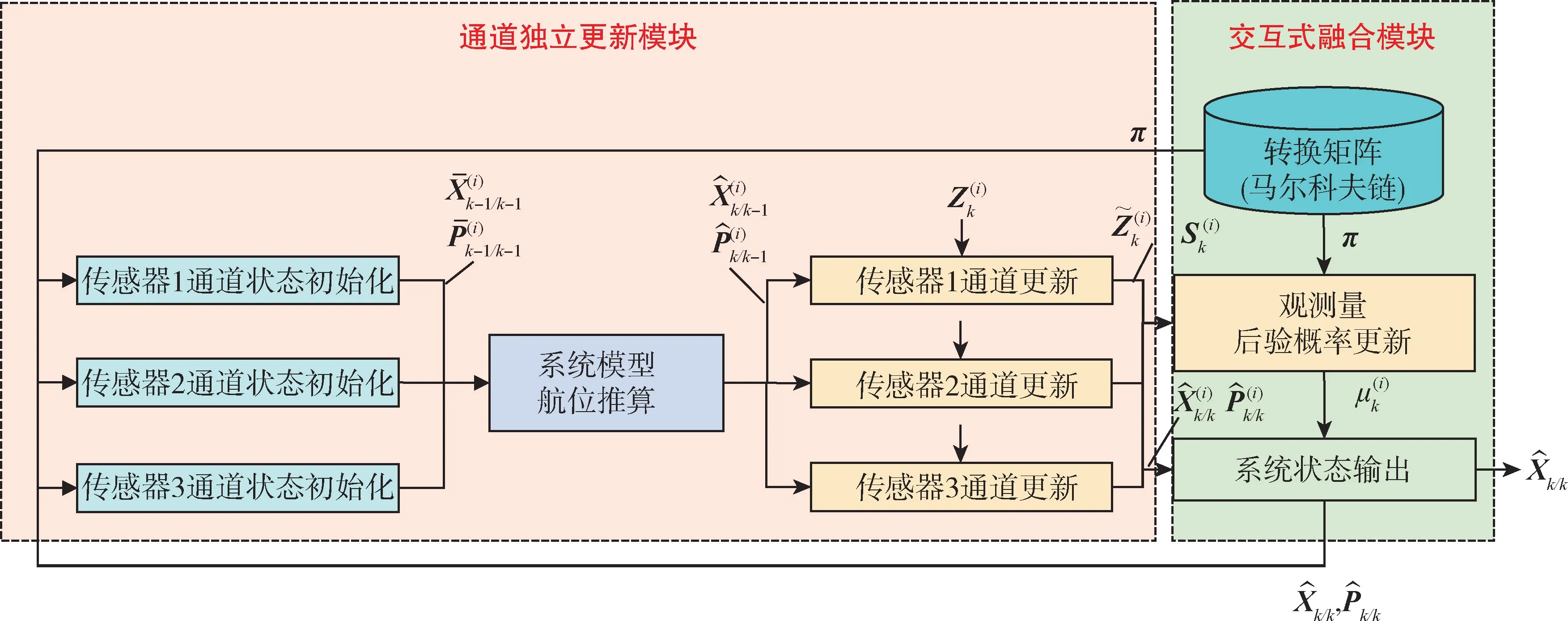
图1 基于传感器独立更新的弹性融合框架Fig.1 Resilient fusion solution based on sensor-independent-update

1.1 观测传感器独立滤波

以上标“（i）” 表示第i个独立观测传感器更新通道,在k-1 时刻的状态估计矩阵和误差协方差矩阵为和;在k时刻,测量矩阵为,系统的转移矩阵为Φk,系统的噪声矩阵为Qk,观测矩阵为,测量误差的误差矩阵为R（i）k。滤波流程如下:

（1）状态估计

（2）协方差状态估计

（3）卡尔曼滤波增益

（4）状态更新

（5）协方差矩阵更新

1.2 交互式弹性融合

在状态域对各个独自并行滤波的传感器进行数据融合,有

式（6） 中,Zk为总数为M的观测传感器集合,为模型的后验估计概率。

当观测量没有故障时,可以获得第i个传感器的最小均方根估计

为了更新后验估计权重,需要求得模型在k时刻的最大似然函数

传感器先验转换概率以马尔科夫链的形式存储在转换矩阵中,提供的是各传感器先验置信度,与模型似然参数一起根据贝叶斯原理通过交互式融合决定各通道的后验概率

为基于k-1 时刻的先验概率并且会被引入到接下来的状态更新部分之中。

最终,输出的状态估计和状态协方差为各个独立更新状态的加权结果

2 城市峡谷场景下的实验验证与分析

本节将通过实验验证交互式弹性融合算法在复杂挑战环境下的可行性。针对城市峡谷环境下的动态车载实验,分别用本文提出的弹性融合方法和传统扩展卡尔曼滤波方法进行数据处理和定位解算,对比定位误差以及算法对不同导航源信号的处理情况。

2.1 实验设置与数据预处理

本实验采用香港理工大学智能导航定位实验室所提供的开源数据[15],数据集在香港尖东地区进行采集。实验场景以及运动轨迹如图2所示,该地区为集中的商业娱乐区,周围的建筑物高大且密集,是一个典型的城市峡谷环境。数据为车载动态采集,时长超过450s。相关导航传感器的信号信息如表1所示,包含惯性导航单元、卫星导航系统、激光雷达系统和视觉相机等典型导航传感器。

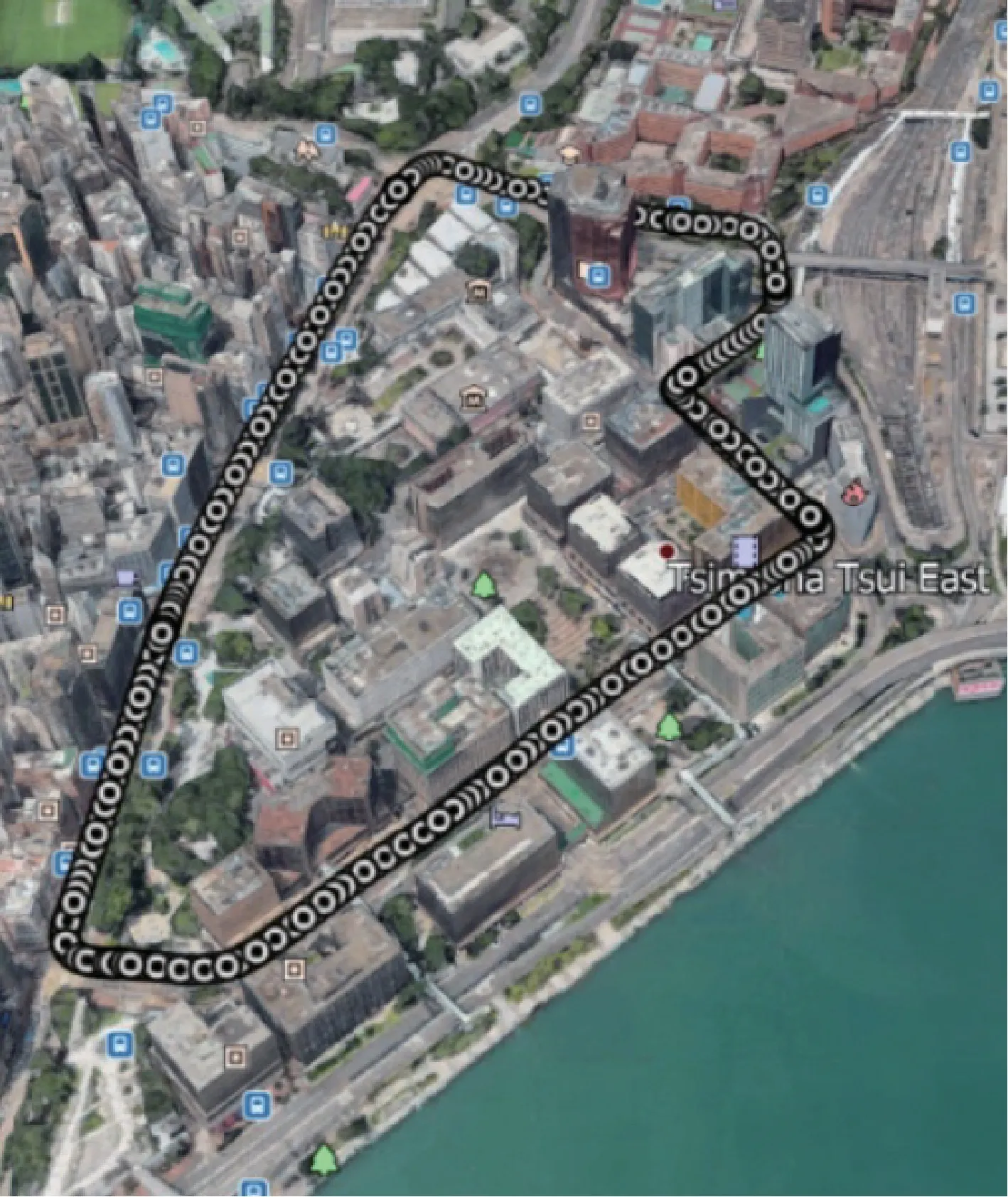
图2 香港尖东地区车载数据轨迹Fig.2 Kinematic trajectory in East Tsim Sha Tsui,Hong Kong

表1 导航传感器类别及型号Table 1 Classifications and types of navigation sensors

卫星接收机的天线和激光雷达、相机摄像头均安装在车顶,不同坐标系提前进行标定,并采用Novatel SPAN-CPT 导航系统所获得的导航定位数据作为参考轨迹。

2.2 实验结果与数据分析

GNSS、激光雷达和视觉三种导航观测传感器的独立定位效果和精度如图3和表2所示。相关结果表明,在城市峡谷环境下,卫星信号受建筑物遮挡和信号折射非常严重,传统GNSS-RTK 定位模式几乎无法固定,只能采用单点定位模式,定位结果不仅平均误差很大且跳变频繁,无法满足定位需求;视觉定位VINS 随着时间的推移误差累积情况非常严重;激光雷达的定位精度在三者中效果最好,但是相对定位的模式导致在部分地段累积误差也较大。单一导航源都很难在复杂挑战环境下提供可靠的定位导航结果。

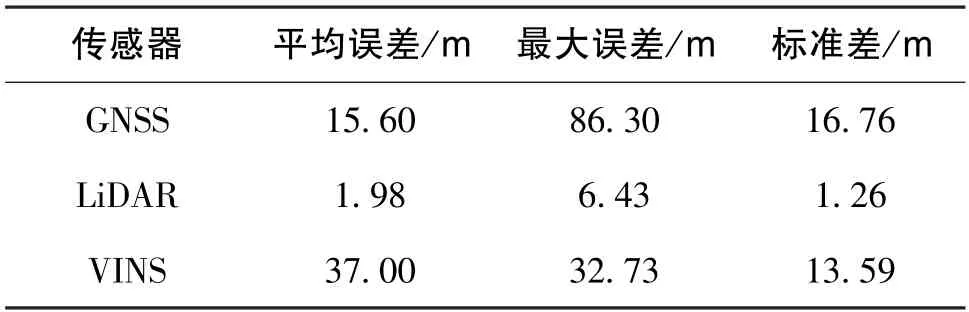
表2 独立导航源定位误差Table 2 Positioning errors of single navigation sensor

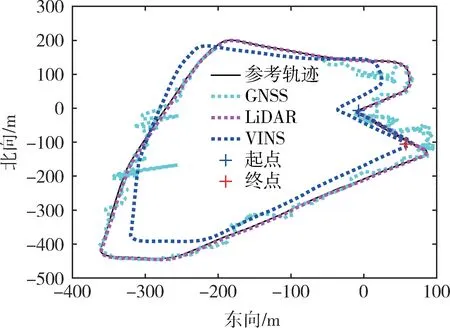
图3 独立导航源传感器观测值定位结果Fig.3 Positioning results of single navigation sensor

本文采用INS/GNSS/LiDAR/VINS 的多源融合松组合模型,系统模型采用15 维的状态矢量

式（14）中,δφ、δv、δp分别为三维运动姿态、速度和位置误差向量,δba、δbg为加速度计和陀螺仪的偏差向量。

观测向量为

式（15） 中,pGNSS、pLiDAR分别为GNSS、LiDAR定位坐标的三维输出,ΔpVINS为VINS 的相对坐标输出。

鉴于在城市峡谷环境下LiDAR 的定位精度最高、GNSS 和VINS 的定位精度均不太理想,本实验中弹性融合方法的传感器优先级马尔科夫链设置为

经典扩展卡尔曼滤波与弹性融合算法的定位结果如图4和表3所示。其中,平均误差指的是在每个历元的平均定位误差,标准差为此次实验中所有历元的标准差,最大误差为所有历元定位误差中的最大值。

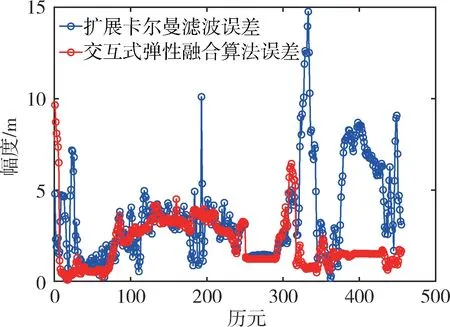
图4 数据融合定位水平面误差对比图Fig.4 Positioning errors comparison of information fusion in horizontal direction

表3 扩展卡尔曼滤波和交互式弹性融合算法的定位误差对比Table 3 Positioning errors comparison between EKF and interactive resilient fusion algorithm

实验结果表明,在均没有增加故障检测和隔离功能的情况下,弹性融合算法相比传统EKF 算法,在平均误差、标准差和最大误差方面均展现出明显的优越性。尤其在运动实验的后半段,随着环境变化以及LiDAR、VINS 的相对误差累计,EKF 算法下的定位误差明显上升,并且出现接近15m 的最大定位误差,而弹性融合算法除最开始滤波收敛的5 个历元外,全程定位精度均明显优于EKF,并且对粗差的鲁棒稳定性更好。

为进一步分析弹性融合算法的权重更新以及故障隔离效果,对弹性融合过程中各个独立导航源通道的后验概率和似然函数结果展示如图5所示,统计结果如表4所示。

图5 弹性融合算法中观测传感器的后验概率与似然估计Fig.5 Posterior probabilities and model likelihoods of observable sensors in resilient fusion

表4 各传感器后验概率与似然估计均值Table 4 Means of posterior probabilities and model likelihoods for observable sensors

上述结果表明,GNSS 的μk几乎全程为0,即算法在交互式融合过程中几乎全程将其排除在外,动态权重的调整起到了天然的故障检测与隔离效果。LiDAR 和VINS 的μk分别大致在0.8 和0.2 左右浮动,可见算法认定LiDAR 和VINS 的定位精度更高,认为这两者更可靠。这其中,LiDAR 的μk远大于VINS 的,说明在城市峡谷环境中LiDAR 的定位是最可信的,这与单传感器的定位结果分析是相吻合的。各传感器模型似然函数的输出结果也验证了算法对观测传感器的动态优选过程,从各传感器模型似然函数值中可看出,LiDAR 的模型似然函数值最大,其次是VINS。GNSS 的模型似然函数值几乎为0,系统几乎将其定位结果排除在外,这与对各传感器的后验概率分析所得出的结论一致。

4 结论

本文提出了一种基于观测传感器独立更新的多源导航信息弹性融合架构。各观测传感器均在独立通道中对系统状态进行更新,可以有效降低不同观测传感器在信号融合层面的耦合度,并且各传感器可以采用最个性化的方式进行滤波或优化。后端交互式滤波结合各传感器先验信息,只对定位域状态信息进行融合输出。传感器的剔除或引入均保持通道切换模式,在保持对可用传感器开放性的同时保证了信号处理环路的稳定性和弹性。在典型城市峡谷环境下的动态车载实验充分验证了方法的优越性,通道更新架构和权重动态更新可以起到很好的故障隔离和传感器动态优选,定位精度和鲁棒性均明显提高。