基于ISSA-BP的500kV高压线损预测模型

徐利美,贺卫华,李 远,杨 射,刘展鹏,续欣莹

(1.国网山西省电力公司,山西 太原 030021;2.国网山西超高压变电公司,山西 太原 030021;3.太原理工大学 电气与动力工程学院,山西 太原 030024)

0 引 言

全球能源危机不断加剧,降损是改善电力资源浪费的有效途径,此过程需要对线损进行准确、可靠的预测[1]。电能通过输电、变电等设备时,由于设备之间存在阻抗,就会产生电能损耗,这个损耗称为线损[2]。线损率是指向电网中供应单位电能产生的电能损耗。线损率作为电力系统中的重要指标,在很大程度上可以反映出电网运行的经济性。

高压输电线的线损主要包括电阻损耗和电晕损耗。电阻损耗由于电流流过输电线时发热而产生,其主要与输电线的材质及电流大小有关。电晕损耗主要与气象条件有关,由于导线表面的空气被击穿,电能转换成光和热等其他形式的能量而产生。降雨时,导线表面最大场强增加,电晕损耗也会明显增大[3]。

山西电网依靠其丰富的煤炭资源、适中的地理位置,在西电东送、南北互供、全国联网的总体布局中占据着重要的地位[4]。为了对山西省北部某段500 kV电压等级输电线的线损情况进行分析,准确预测此段线路的线损率,有必要对其进行专门研究。

现如今,理论线损的计算方法应用已经相当广泛,有等值电阻法[5]、均方根电流法[6]等。但上述方法均无法考虑气象因素对线损的影响。近年来,人工智能技术得到了快速的发展,神经网络算法在很多领域都得到了应用,这也为线损预测提供了新的方法。文献[7]采用BP神经网络对线损进行预测。但BP神经网络的初始权值和阈值是随机确定的,导致预测精度受到影响。文献[8]采用改进的BP神经网络对线损进行预测,此方法可以对低压配网的线损进行很好的预测,但无法对高压线损进行准确预测。文献[9]采用了优化的反向传播神经网络来对线损进行预测。该方法与传统的人工神经网络方法相比,具有了更高的精度和收敛速度,但有可能出现过拟合的情况。文献[10]采用LM算法优化BP神经网络的方法对线损进行预测。优化后的 BP 神经网络相较标准BP神经网络其收敛速度明显提升,但有可能出现陷入局部极小值的情况。文献[11]改进了BP算法中的梯度下降法,虽然BP神经网络的计算性能得到了提高,但没有研究输入层如何对电气参数进行确定。文献[12]采用遗传算法优化BP神经网络的方法对线损进行预测,但遗传算法容易早熟收敛,导致网络在训练过程中会出现陷入局部最优解的情况。

BP神经网络结构简单,使用方便,但其对初始权值及初始阈值的选择较为敏感,不同的初始权值和阈值会使网络收敛于不同的局部最优值。可利用智能优化算法优化BP神经网络的初始参数。麻雀搜索算法(Sparrow Search Algorithm,SSA)[13]于2020年被提出,SSA收敛速度快、收敛精度高,但容易早熟收敛,对其改进可以提高SSA的寻优能力。因此,该文提出了一种基于改进麻雀搜索算法(Improved Sparrow Search Algorithm,ISSA)优化BP神经网络(ISSA-BP)的高压线损预测模型,并以实际高压输电线线损样本数据为例进行试验。结果表明,利用ISSA-BP模型进行线损预测,可以提高模型的预测精度。

1 相关工作

1.1 BP神经网络

BP神经网络具有较强的非线性映射及自适应能力,在预测领域得到了广泛的应用。BP神经网络由输入层、隐含层和输出层构成,通常具有3层及以上的结构。3层BP神经网络结构如图1所示。

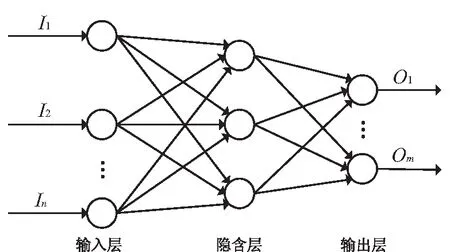
图1 3层BP神经网络结构

图1中,Ii(i=1,2,…,n)表示网络的输入;Oj(j=1,2,…,m)表示网络的输出。BP神经网络的学习过程包括信号的正向传播和误差的反向传播两个阶段。在第一阶段,网络输入信号从输入层传递到隐含层,经过隐含层激活函数的激活操作后再传递到输出层。经过隐含层激活函数作用后,可以将隐含层的输出控制在0～1的范围内,接着再传递到输出层。在第二阶段,网络根据预测值与标签值的误差对比结果进行反向传播,通过调整各神经元之间的权值和阈值,使得整个网络向误差减小的方向不断更正[14]。

1.2 麻雀搜索算法

在一个种群中,有发现者、加入者和警戒者三种类型的麻雀,每一只麻雀都对应着一组可能的初始权值及初始阈值[15]。

SSA在每次迭代时,发现者位置更新表示为:

(1)

SSA在每次迭代时,加入者位置更新表示为:

(2)

SSA在每次迭代时,警戒者位置更新表示为:

(3)

2 改进的麻雀搜索算法

2.1 麻雀搜索算法的改进策略

传统SSA具有容易陷入局部最优及早熟收敛的缺点。该文将Lévy变异引入发现者机制,将旋转策略引入加入者机制,以此增强SSA的寻优能力。

(1)Lévy 变异策略。

Lévy分布[16]是非负随机变量的连续概率分布,其数学表征为:

(4)

其中,μ为位置参数,c为标度参数。相较于Gaussian分布与Tent分布,Lévy分布产生的随机数其随机性与分布均匀性均为最强,因此Lévy分布能对搜索空间进行更好、更高效的搜索。

通常迭代次数过半时进入迭代后期。设置迭代次数为100,经实验得出,迭代次数为65～75时效果最好。因此,该文设置迭代次数为65～75时引入Lévy变异策略。改进后的发现者位置更新公式为:

(2)旋转策略。

受状态转移算法(State Transition Algorithm,STA)[17]中旋转策略启发,将旋转策略引入加入者机制中,扩大加入者搜索范围,避免算法早熟收敛。改进后的加入者位置更新公式为:

(6)

其中,εα称为旋转因子,旋转策略的引入可以使生成的候选解在半径为εα的超球里。其数学原理如式(7)所示:

(7)

在式(6)中,当εα取值较大时,搜索空间变大,算法全局探索能力增强;反之,当εα取值较小时,算法局部开发能力增强。为避免算法出现早熟收敛现象,该文对参数εα进行重新设计,重新设计后的εα表示为:

(8)

2.2 改进麻雀搜索算法的性能测试

为验证ISSA算法的有效性,选取了6个基准函数对ISSA进行测试。其中,F1～F3为单峰基准函数,F4～F6为多峰基准函数。基准函数表达式如下:

(9)

(10)

(11)

(12)

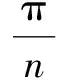
(13)

F6(x)=0.1{sin2(3πx1)+

(xn-1)2[1+sin2(2πxn)]}+

(14)

基准函数具体信息如表1所示。

表1 基准函数具体信息

为了测试ISSA的寻优能力是否得到提升,将灰狼优化算法(Grey Wolf Optimizer,GWO)[18]、鲸鱼优化算法(Whale Optimization Algorithm,WOA)[19]、SSA及ISSA在上述6个基准函数上进行测试。其中,WOA中的对数螺旋形状系数b=1,GWO、WOA、SSA与ISSA种群数量均设定为30,最大迭代次数均设定为1 000,实验均独立重复运行30次,取30次实验结果的平均值及标准差。测试结果如表2所示。

表2 基准函数测试结果

续表2

3 ISSA-BP高压线损预测模型的建立

BP神经网络的初始权值和阈值为0～1之间产生的随机数,每次训练都会得到不同的结果,多次训练后才会选择拟合较好的一个网络[12]。该文采用ISSA对BP神经网络的初始权值和阈值进行优化。以某条实际高压输电线路为研究对象,在综合考虑了此输电线路相关数据获取的难易程度以及线路运行实际情况之后,决定选取关口电压、关口电流、温度和相对湿度这四个特征参数,综合研究上述特征参数对高压线损的影响。

ISSA优化BP神经网络的具体流程如下:

Step1 数据归一化。由于各维度输入数据差异性较大,需对输入数据做归一化操作,经归一化处理后的样本数据位于[-1,1]之间,计算公式如下:

(15)

Step2 确定BP神经网络的结构,并初始化网络参数。由于模型输入为关口电压、关口电流、温度和相对湿度,输出为线损值,因此BP神经网络的输入层节点数为4,输出层节点数为1。隐含层节点数过大或过小都会影响网络的预测精度,通过反复测试,最终确定隐含层节点数为16;

Step3 初始化ISSA。设置ISSA搜索维度、最大迭代次数、麻雀种群规模、发现者数量、加入者数量、警戒者数量及预警值;

Step4 计算每个麻雀个体的适应度并排序。适应度表示ISSA中种群个体的优劣情况,该文采用均方误差(Mean Square Error,MSE)作为ISSA的适应度函数,MSE的表达式为:

(16)

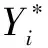
Step5 更新麻雀位置。按式(5)更新麻雀种群中发现者位置,按式(6)更新种群中加入者位置,按式(3)更新种群中警戒者位置,并计算更新后麻雀的适应度值;

Step6 判断模型是否满足结束条件。当算法的循环次数达到最大迭代次数时,算法终止。否则,算法返回到上一步,继续更新麻雀位置;

Step7 输出适应度最小的麻雀位置。当模型满足结束条件时,模型输出适应度最小的麻雀位置,即输出BP神经网络的最佳初始权值和最佳初始阈值;

Step8 高压线损预测。将ISSA寻找的最佳初始权值和阈值赋予BP神经网络,网络通过误差反向传播的方式不断更新权值和阈值,当达到最大迭代次数时,输出高压线损预测值。

ISSA-BP算法流程如图2所示。

图2 ISSA-BP 算法流程

4 实验仿真

4.1 实验环境及参数设置

实验仿真时计算机主要硬件配置如下:CPU为Intel®CoreTMi5-7200U,基准频率为2.50 GHz;仿真软件为 MATLAB2018b。

BP神经网络的输入层、隐含层和输出层节点数分别为4、16和1,因此共有4×16+16×1=80个权值,16+1=17个阈值。设置ISSA搜索维度为80+17=97,麻雀数量为20,最大迭代次数为100,发现者占比0.2,加入者占比0.7,警戒者占比0.1,预警值为0.8。按照图2所示算法流程训练模型。

4.2 实验数据及预处理

为了验证ISSA-BP模型的有效性,选取山西省某条高压输电线路在2021年6～8月份的关口电压、关口电流、温度和相对湿度数据,数据采样周期为15分钟,对数据进行分析并剔除异常值后,得到8 000组数据。随机选择其中的7 900组数据作为训练集,其余100组数据作为测试集。

4.3 评价指标

该文选取均方根误差(Root Mean Square Error,RMSE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)、平均绝对误差(Mean Absolute Error,MAE)和决定系数(Coefficient of Determination,R2)为性能评价指标,RMSE、MAPE、MAE和R2的表达式如下:

(17)

(18)

(19)

(20)

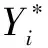
4.4 结果分析

BP、GWO-BP、WOA-BP、SSA-BP与ISSA-BP迭代次数均设置为100,使用上述模型对测试集中的100条样本数据进行预测。五种模型的预测结果及误差(真实值-预测值)分别如图3～图7所示,预测结果的局部放大如图8所示。

由图3～图8可以看出:以上五种预测模型中,BP网络预测模型效果最差,当线损发生剧烈波动时,其预测值与实际值偏差较大,不能很好地反映线损的真实情况。GWO-BP、WOA-BP、SSA-BP与ISSA-BP模型的预测精度相较于BP神经网络均有所提高。ISSA-BP模型的预测效果最好,即使线损出现波动较大的情况,其误差也能保持较小的值,预测曲线可以与实际曲线很好地拟合。

图3 BP网络预测结果

图4 GWO-BP预测结果

图5 WOA-BP预测结果

图6 SSA-BP预测结果

图7 ISSA-BP预测结果

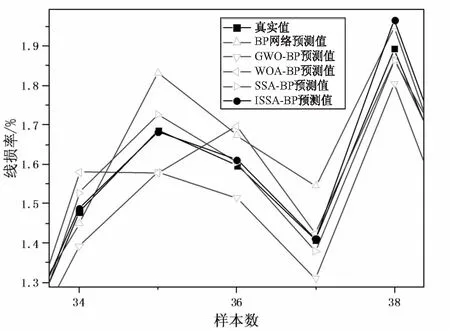
图8 预测结果局部放大

使用上述评价指标对五种模型的预测效果进行评价,得到的误差统计如表3所示。

表3 误差统计 %

从表3可得,使用以上五种模型进行线损预测时,BP网络预测精度最低,其RMSE、MAPE、MAE与R2分别为9.06%、8.20%、7.98%与95.59%,均为预测模型中最差。BP网络经过GWO、WOA、SSA与ISSA优化后,预测误差都有明显降低。其中,ISSA-BP预测效果最佳,其RMSE、MAPE、MAE与R2分别为4.29%、3.67%、3.57%与99.01%,均为预测模型中最优。相较于BP网络,ISSA-BP的RMSE下降了52.6%,MAPE下降了55.2%,MAE下降了55.3%,R2提高了2.18%。相较于SSA-BP网络,ISSA-BP的RMSE下降了33.4%,MAPE下降了36.7%,MAE下降了37.1%,R2提高了1.24%。结果表明,通过ISSA优化BP神经网络的初始权值和阈值,可以有效提高高压线损的预测精度。

5 结束语

为了更准确地对500 kV高压线损进行预测,综合考虑温湿度等特征参数的影响,提出了一种基于ISSA-BP的高压线损预测模型。传统SSA在迭代后期容易陷入局部最优值,导致其优化BP神经网络的效率降低,该文对SSA中发现者及加入者位置更新方式进行改进,并在6个基准函数对ISSA进行性能测试,结果表明,ISSA的寻优能力有了很大提升。为验证将ISSA-BP模型用于提高线损预测精度的有效性,以实际高压输电线路为研究对象进行试验,结果表明,通过ISSA优化BP神经网络,能在很大程度上提高模型的预测精度。