金融业与实体经济间系统性风险溢出效应研究——基于GARCH-QRNN-POT模型*

● 王子仪，李 磊

（新疆财经大学 统计与数据科学学院，新疆 乌鲁木齐 830012）

一、引言

近年来，随着金融制度、工具、技术、业务以及新市场的开拓，金融市场飞速发展，但同时也对监管提出了更高的要求。历次系统性风险的爆发间隔不断缩短，涉及范围不断扩大。拉美债务危机、亚洲金融危机、美国次贷危机及其引发的国际金融危机等一系列波及范围极广、危害程度极大的系统性风险的爆发极大的阻碍了区域、甚至是世界经济的发展。如今各个行业间不仅存在产业链这种方式的实体联系，还通过金融市场这种金融联系紧密相连，使得系统性风险的传播范围也更广[1]。

系统性风险的传导可以划分为国内传导和国际传导。国内传导包括个体机构的部门间传导、机构间传导以及市场间传导。部门间传导因机构业务联系而产生；机构间传导则是源于不同机构间的经济活动关系；金融市场化加深了市场间的联系，但也为市场间传导提供了便利。国际传导主要通过贸易往来和金融途径，经济全球化促进了不同国家之间联系，但也为系统性风险的国际传导奠定了基础。以2008 年的金融危机和2020年新冠肺炎疫情为例进行简要分析，二者的风险传染路径是完全不同的。2008 年的金融危机源于2007 年美国的次贷危机，在低利率环境下信贷快速扩张，当房价下跌和加息出现后爆发偿付危机，大量持有与其相关金融衍生品的金融机构破产，进而冲击了美国资本市场，随后席卷各国市场，我国股票市场也受其冲击，由于我国的资本管制较严格削弱了直接冲击[2]，但间接冲击仍不可估量。2020 年新冠疫情对各个国家、经济体产生巨大冲击，全球范围内的各个行业均受其波及，实体经济遭受了二战以来最严重的经济衰退。国外实体行业业绩下滑，物价水平上涨，全球供应链紧张甚至中断，对全球实体经济造成严重的冲击，并通过资金链、产业链等传导至金融市场，同时通过影响投资者情绪的途径加剧金融市场动荡[3]，可能促使原本积累的金融风险提前爆发；甚至通过海外市场影响到我国金融业，导致我国金融业系统性风险上升[1]；金融业的内部风险也会通过信贷、债券、证券等金融联系溢出至其他实体行业[4]。因此，对于系统性风险的准确识别以及基于更广的视角研究系统性风险的溢出效应就更具必要性和重要性。

二、相关研究文献评述

（一）系统性金融风险的测度方法

对于系统性风险的度量方法，根据国内外学者的文献，大致可以分为四类：

第一类：系统未定权益分析方法（SCCA）

该方法是一种前瞻性的框架，可以度量市场中潜在的金融机构预期损失的系统偿付能力风险。国内学者张炜[5]选取上市银行的市场数据，通过或有期权定价模型（SCCA 方法的基本原理）和时变Copula 函数构建商业银行系统性风险评价指标，并将其引入到包含房地产市场及宏观数据的SVAR 模型中研究房价与系统性风险间的联系，研究发现：房价上涨伊始会降低系统性风险，但最终会形成系统性风险。刘超等学者[6]拓展SCCA 方法的相应指标，结合Gumbel Copula连接函数刻画证券公司间的风险相依结构，并发现系统性风险爆发前往往会存在部分公司同时表现出的小型波动的前兆；证券公司的系统性风险具有“急增缓降”的特点且在风险传播阶段形成的数次冲击对整个系统具有较大的破坏力。

第二类：构建指标体系方法

该方法采用因子分析或CRITIC 赋权法等方法构造金融压力指数，该指标可以捕捉到当期系统内的压力水平。ling 等[7]率先编制的金融压力指数被各国监管当局所采用，对系统性金融风险的关注着重于流动性风险和清偿能力风险方面。马骏等人[8]从系统性金融风险爆发时期各市场间联动性显著增强这一特点的角度出发，构建用以识别系统性金融风险的金融压力指数，结果表明：该指标具有很好的稳健性，可以起到监控金融市场压力的作用。李敏波和梁爽[9]从金融压力指数频度的角度出发，使用交易数据构建日度金融压力指数，弥补以往金融压力指数的滞后性问题，用以识别系统性金融风险。许涤龙和陈双莲[10]基于CRITIC 赋权法构建金融压力指数，并从银行、房地产、股市和外部金融市场四个方面综合测度我国面临的金融压力。田军等人[11]通过选取五个维度（金融机构、资本市场、货币市场、房地产市场和金融科技发展）的若干基础指标构造了我国系统性金融风险综合指数，反映了我国系统性金融风险走势和主要影响因素。

第三类：动态随机一般均衡模型（DSGE）

Zhiguo 等[12]认为当冲击导致金融机构中介作用中断，对经济产生不利影响，并进一步反馈到金融机构自身时，系统性风险就会产生。并在其模型中假定经济状态只存在正常状态和系统性风险状态，通过估计经济向系统性风险状态转变的概率来测度系统性风险。李力等人[13]将企业细化为政府融资平台企业和其他企业，使用DSGE 模型探究货币政策对经济波动的影响途径，研究发现：宽松的货币政策会提高两类企业的违约率，但由于两类企业背景不同，融资平台企业净值反而逆势上涨，最终导致政府违约风险上升。吴东霖和赵玮[14]将金融加速器效性引入到包含居民、企业、银行和央行的DSGE 模型中，研究商业银行受到不同程度的资本监管时对经济产生的影响，研究表明：监管力度的小程度提升有助于遏制系统性金融风险；而严格的资本监管会使经济波动加大。

第四类：增量条件在险价值模型（ΔCoVaR）

Adrian 等[15]提出了CoVaR，其内核为金融系统的在险价值（VaR）。梁斯[16]先使用CRITIC 法对各金融子市场的交易指标数据进行整合，再使用EGARCH-CoVaR 模型测度不同市场的系统性风险及其对整个金融市场的风险溢出程度，研究发现：股市对整体金融市场的系统性风险贡献最大。佟孟华等[17]基于分位数回归和CoVaR 方法研究非系统重要性银行（非四大国有银行）对银行业系统性风险的影响，结果表明：四大行以外的银行在风险传导过程中起到了中介作用，通过对四大行产生冲击，从而诱发银行业系统性风险。刘海云和吕龙[18]在增量条件在险价值分析方法的基础上结合网络关联分析，探究全球股市风险扩散的整体情况，研究表明：风险主要在金融市场开放度高的国家间扩散，发达国家对外的溢出程度最高，而发展中国家在国际市场中主要作为外溢风险的接收者。

第五类：网络关联分析方法

网络关联分析的思路是构建一个机构间的风险敞口矩阵，用以分析各个机构的违约后果及其后续影响。苗文龙等人[19]根据国际银行部门的债权债务数据构建国际信贷网络，研究国际信贷网络结构变动对系统性金融风险的影响，结果表明：国际金融体系的风险状况主要取决于发达国家金融体系的稳定性及其交易规模的波动性。徐国祥等人[20]基于上市银行年报、股票收益率及评级数据构建银行间拆借矩阵和风险传染网络，用以研究不同银行所引发的系统性风险损失和政府监管的介入效果，研究表明：上市银行规模与其他银行的相关性是其所引发的系统性风险的决定因素；政府监管的介入可以有效缓解系统性风险的积累。李湛等人[21]基于VAR 模型构建风险溢出指数，并根据风险溢出指数构建金融风险溢出网络，用以分析我国金融子市场间的风险溢出水平及变动趋势，结果表明：我国系统性金融风险溢出效应整体水平较高，各市场间联动性较强，且货币市场始终是风险的溢出方。

（二）金融与实体的相互影响

对于金融与实体间相互影响的研究则较少，目前国内外的研究主要集中在金融市场内部、金融子版块与子版块之间、金融市场与能源市场之间、金融市场与房地产市场之间，鲜有涉及金融市场与实体经济间的风险度量及传播。彭俊华和许桂华[22]从七个维度构造系统性金融风险综合指数，运用VAR 模型证实了房价异常波动会导致市场（信贷市场、资本市场）及政府资源错配，进而演变为系统性风险。翟永会[23]使用时变Copula函数刻画我国实体子行业与银行业间的两两相依关系，在此基础上度量二者间的系统性风险溢出强度，结果表明：实体子行业与银行业间存在双向的风险溢出关系，且呈时变特征。何青等人[24]基于主成分分析分位数回归法构造系统性金融风险指数，并基于此探究金融与实体经济间的风险传导途径，结果表明：信贷途径是系统性金融风险扩散到实体经济的首要传导途径。周开国等人[25]运用GARCH-in-Mean 模型研究中国股市风险与宏观经济的相互影响，结果表明：两经济领域变量的均值和波动率都存在双向影响；且风险传导效应在不同时期存在显著差异。陈守东等人[26]基于极值理论研究了不同金融机构的尾部风险异质性及行业间的相关性，研究发现：行业间尾部风险相关性随极端金融事件的发生而上升；房地产行业在股市动荡时期是金融风险的主要输出者。张超和张文蕾[27]使用DCC-GARCH-CoVaR 模型测度我国房地产业对银行业的系统性风险溢出效应，并从行业和企业两个层面分析溢出过程，结果表明：房地产业对银行业在两个层面都存在显著的溢出效应，原因在于银行持有的房地产信贷敞口比例过高。贾妍妍等人[28]运用LASSO-VAR 模型从部门的角度考察金融体系在中国经济系统中的作用，研究发现：中国经济系统的风险源是实体经济；而金融体系在其中起到了吸收风险的作用。何红霞和武志胜[29]从平均波动和左尾损失的视角出发，研究金融对实体经济的风险溢出效应，研究发现：金融对实体经济同时存在波动溢出和左尾风险溢出两种效应；且行业特征对左尾风险溢出效应存在显著影响。杨佩娟和陈少凌[30]运用GARCH-in-Mean 模型研究实体与金融间的风险传导机制，研究发现：适度控制企业的杠杆率可以有效降低企业对金融系统的依赖，控制实体部门对外溢风险的接收。

结合研究问题的特点及上述方法在两市场间的适用性，本文选取增量条件在险价值模型并结合极值理论、神经网络分位数回归（QRNN）及GARCH 族模型刻画金融市场和实体经济间的风险溢出效应；未采用常用的Copula 函数链接方法原因在于EVT 更注重序列的尾部分布情况，可以对VaR 进行更准确的度量，且具有泛化能力[31]，并考虑到陈坚[32]已在VaR 框架下对Copula 函数和极值理论两种方法进行了性能比较，结果表明：基于极值理论的风险度量准确度更高，更符合现实情况；而神经网络分位数回归在拟合金融数据非线性与非对称性结构方面具有极好的表现；GARCH 族模型则可以很好的拟合序列的波动积聚效应。

本文的贡献在于，将GARCH 族模型与神经网络分位数回归相结合，并借助极值理论实现极端情况（显著性水平为1% 及以下）与正常情况（显著性水平为5%）间的转化，运用于实体经济与金融行业间系统性风险的溢出效应研究领域，扩充了该领域的研究方法。在当今这个行业融合发展的时代，本文研究为实体经济与金融行业的系统性风险度量和风险溢出提供了有益参考。

三、GARCH-QRNN-POT 模型

本文首先介绍风险度量的强度指标（VaR 和CoVaR）及模型效果的检验指标（Kupiec 失败率检验法），其次介绍理论模型，再次阐明研究步骤及模型优势。

（一）风险强度指标及检验指标

在险价值VaR 表示在正常情况下，某一资产在给定的置信水平下在其持有期内可能发生的最大损失，是当前系统性金融风险测度中应用最广的方法。VaR 的数学表达式如下：

其中，rt为资产在正常市场条件下持有期内的收益率；VaR 为置信水平c 下的在险价值。

条件在险价值CoVaR 的含义是当某一市场i的风险损失值为VaR 时，其他市场j 受其波及所遭受的最大损失，它是对VaR 的拓展，实际上也是个分位数，也要求必须在一定的置信水平下。CoVaR 的数学表达式如下：

在险价值仅关注孤立的个体风险，而条件在险价值的出发点是行业间的相互联系，因而在测度风险溢出效应方面应用极广。本文采用更加适合度量极端风险的分位数回归方法计算CoVaR，根据模型（3）建立分位数回归模型：

将Xi取为时，即可得到：

而增量条件在险价值ΔCoVaR 可以表示为：

为便于比较，对ΔCoVaR 处理得到%CoVaR：

运用Kupiec 失败率检验法检验模型效果：首先，将VaR 与实际损失比较。VaR 小于实际损失表明此次风险度量效果较差，未能有效估计出潜在风险；VaR 大于实际损失表明此次风险度量成功，可以有效估计出潜在风险。其次，失败次数N除以总观测次数T 记为实际失败率p。最后，构建LR 统计量检验实际失败率是否与预期失败率（显著性水平）相一致，LR 统计量服从卡方分布。

该方法将模型估计的在险价值和实际损失进行比较，原假设为p=α，在一定的接受范围内通过检验，则表示模型估计的VaR 值为有效值。

（二）理论模型

采用标准的GARCH(1，1)模型形式如下：

其中，xt=(x1t,x2t,…,xkt)'是解释变量向量，γ=(γ1,γ2,…,γk)'是系数向量，模型（9）被称作均值方程，模型（10）被称作条件方差方程。

若利用GARCH 族模型估算VaR，需要先对扰动项进行假设。本文的对比模型选为多种分布中拟合效果最优的模型①分布形式包括正态分布、偏正态分布、学生t分布、偏学生t分布、广义误差分布和偏广义误差分布。对收益率序列进行拟合，得到均值μt及波动率σt后，VaR 计算公式如下：

其中，F-1(α) 为不同分布假设下扰动项在置信水平为α的分位数。

神经网络分位数回归（QRNN）模型是非线性分位数回归的一类扩展，由Taylor[33]率先提出，并应用于多期价格风险的测度。将神经网络结构引入到分位数回归中，可以模拟金融数据中的非线性结构，同时规避了传统非线性分位数回归可能存在的模型错误设定的问题。Taylor[33]同时证明了多期价格风险的测度主要取决于持有期和波动率，并给出了持有期和波动率的最佳组合形式。由于本文的持有期为1，并考虑到金融市场羊群效应的滞后影响，将波动率序列的自回归形式σt-i作为输入变量(i= 1,2,…,I)，输入到三层的神经网络中，输出层为波动率序列的分位数。隐藏层有J个节点，第j个隐藏层节点gj(τ) 的输出是通过对输入变量和隐藏层权重之间的内积加上隐藏层偏置代入到隐藏层转换函数给出的：

波动率序列的分位数Qt(τ) 是通过对隐藏层输出和输出层权重之间的内积加上输出层偏置b(o)(τ) 代入到输出层转换函数给出的：

可以通过最小化误差函数来拟合数据、估计QRNN 模型的权重和偏置参数：

其中，T为观测数据个数；为防止过度拟合，采用权重衰减正则化和bootstrap 方法，λ是一个正常数，用以控制权值衰减项的相对贡献；由于倾斜绝对值函数ρτ(u) 非处处可微，可采用Huber范数h(u) 逼近：

故此，通过QRNN 模型实现了VaR 值的计算。

极值理论是对极端事件的风险损失进行测度的统计理论方法，它并不关注序列的整体分布情况，而是只注重序列的尾部分布特征，可以在极端条件下对风险进行更准确的度量。本文采用极值理论中的POT 模型与GARCH 族、QRNN 模型相结合，测度金融业与实体行业间的风险溢出情况。POT 模型对超过阈值的样本数据进行建模，着重刻画数据尾部分布特征，但也因此使得可用数据量减小，一定程度上降低了模型的拟合效果。设损失x 为随机变量，其分布函数为F(x)，u为x 的阈值，X 为随机样本中超过阈值u 的样本观测值，则有

其中，Fu(x) 称总体X 对阈值u 的超额分布函数，表示损失超过阈值的条件下，超过部分不足x 的概率。由条件概率公式得：

随着u 的增大，Fu(x) 收敛于广义帕累托分布（GPD）：

当ζ＞0 时，Gu,ζ,β(x) 具有厚尾特征；当ζ= 0时，Gu,ζ,β(x) 具有正常的尾部；当ζ＜0 时，Gu,ζ,β(x)具有截尾特征，但在金融风险管理中通常只考察ζ≥0 时的情况。基于极值理论的VaR 计算问题，可以转换为极值分布的分位数计算问题。由可推得：

又F(u) =P(X＜u)，即不超过阈值u 的观察值在所有观察值中的比例。设观察值总数为n，Nu表示超过阈值的观察值的个数，则有，带入模型（14）中，可得：

反解式（15），得到置信水平α下的VaR 为

（三）研究步骤及模型优势

由于极端情况的可用数据较少，拟合效果不甚理想，本文引入GARCH 族、QRNN 模型提升拟合效果，使其更好地反映现实情况。首先，使用GARCH 模型剔除收益率序列的波动积聚效应，使其满足极值理论的使用条件（独立同分布）；其次，使用QRNN 模型拟合金融数据的非线性结构，并度量正常状况的风险强度，为后续衡量极端情况提供更多的可用数据；最后，使用POT 模型度量极端情况的风险强度，改善了模型对极端数据的处理能力，提升了准确率。受许启发等[34]的启发，对该模型进行了一定的改进，主要研究步骤如下：

1.使用GARCH 族模型剔除收益率序列的波动积聚效应；

2.使用QRNN 模型计算正常情况下处于τ2分位点的分位数Qt(τ2)；

3.计算标准化分位数残差序列：

4.根据分位数定义，使用POT 模型计算极端情况下处于τ1分位点的分位数Qt(τ1)：

对上式进行等价转换：

其中，τ1＜τ2,Qt(τ2) ＜0，Qzt(1 -τ1) 可由POT 模型（22）得到。至此，通过极端分位数与正常分位数间的转化，使度量极端情况的可用数据量增加，从而提升拟合效果，得到极端情况下的VaR 值。

四、金融与实体间系统性风险溢出的实证研究

（一）数据选取

本文所用数据为2007 年9 月14 日—2021年9 月15 日的wind 数据库一级、二级行业分类指数，共计3408 条数据，根据二八原则将2018 年3 月21 日之前的数据作为训练集，2018 年3 月21 日之后的数据作为测试集。其中选取金融一级行业指数代表金融市场；由于缺少代表实体经济的一级行业总指数，仿照wind 行业分类指数构造方法，通过对10 个一级实体子行业指数成交额加权构建代表实体行业的总指数，其中，pt代表实体行业总指数，代表一级实体子行业指数成交额，Wt代表一级实体子行业指数总成交额，代表一级实体子行业指数①一级实体子行业指数包括材料指数、电信服务、房地产、工业、公共事业、可选消费、能源指数、日常消费、信息技术及医疗保健。。行业指数收益率（%）通过对收盘价一阶差分得到rt=(lnpt-lnpt-1) × 100%，数据来源于wind 数据库。

（二）检验及建模

1.描述性统计分析

实体指数和金融指数收益率序列的统计特征如表1 所示，两收益率的均值均较小，分别为0.0078 和0.0039，实体指数的收益率均值略高于金融指数；但二者的标准差均较大，分别为2.2808和1.9239，实体指数收益率的标准差大于金融指数，说明实体指数的收益率波动更大；二者均表现出一定的左偏，但金融指数表现出尖峰特征，而实体指数峰度较低，为2.1164；由于Jarque-Bera 检验易受异常值的干扰，导致检验结果产生偏差，本文采用Shapiro-Wilk 检验和Kolmogorov-Smirnov检验检验两序列是否符合正态分布，两检验均显示实体指数收益率与金融指数收益率不服从正态分布；ADF 检验显示金融指数与实体指数收益率序列均为平稳序列；Ljung-Box 检验显示两序列均存在自相关现象；ARCH 检验显示两序列存在显著的ARCH 效应，即两行业的收益率均存在波动积聚现象，可以建立GARCH 模型。

表1 收益率的统计特征

表2 为金融指数和实体指数收益率序列的Granger 因果检验，结果显示不能拒绝金融波动不能引起实体波动的原假设，也不能拒绝实体波动不能引起金融波动的原假设，即两者相互影响，金融行业与实体经济间存在相互的波动溢出效应。

表2 Granger因果检验

2.基于ARMA-GARCH 模型的VaR

对于既具有尖峰厚尾特性又存在波动积聚现象的金融数据，ARCH 族模型或GARCH 族模型可以刻画其波动性，消除数据的ARCH 效应。因此，选取不同阶数、不同残差分布的ARMAGARCH 模型、ARMA-EGARCH 模型，根据自相关图、偏自相关图、残差是否剔除ARCH 效应、自相关性、AIC 准则和BIC 准则选取最优模型。实体经济选择ARMA(4,2)-GARCH(1,1)-sged 模型；金融行业选择ARMA(4,4)-EGARCH(1,1)-sstd 模型。

实体经济拟合结果由模型（27）给出，ARMA(4,2)-GARCH(1,1)-sged 模型拟合结果如表3 所示，ω 未通过显著性检验（5%），其余参数均通过显著性检验。金融行业拟合结果由模型（28）给出，金融行业ARMA(4,4)-EGARCH(1,1)-sstd 模型的拟合结果（表4）所示，除了参数μ 和α1 未通过显著性检验之外，其余参数均通过了显著性检验。根据模型（11）计算出正常情况和极端情况下ARMA-GARCH 模型测度的实体经济与金融行业的VaR 值，并在测试集上根据模型（8）进行回测检验，结果如表5 所示。

表3 实体经济ARMA(4,2)-GARCH(1,1)-sged模型估计结果

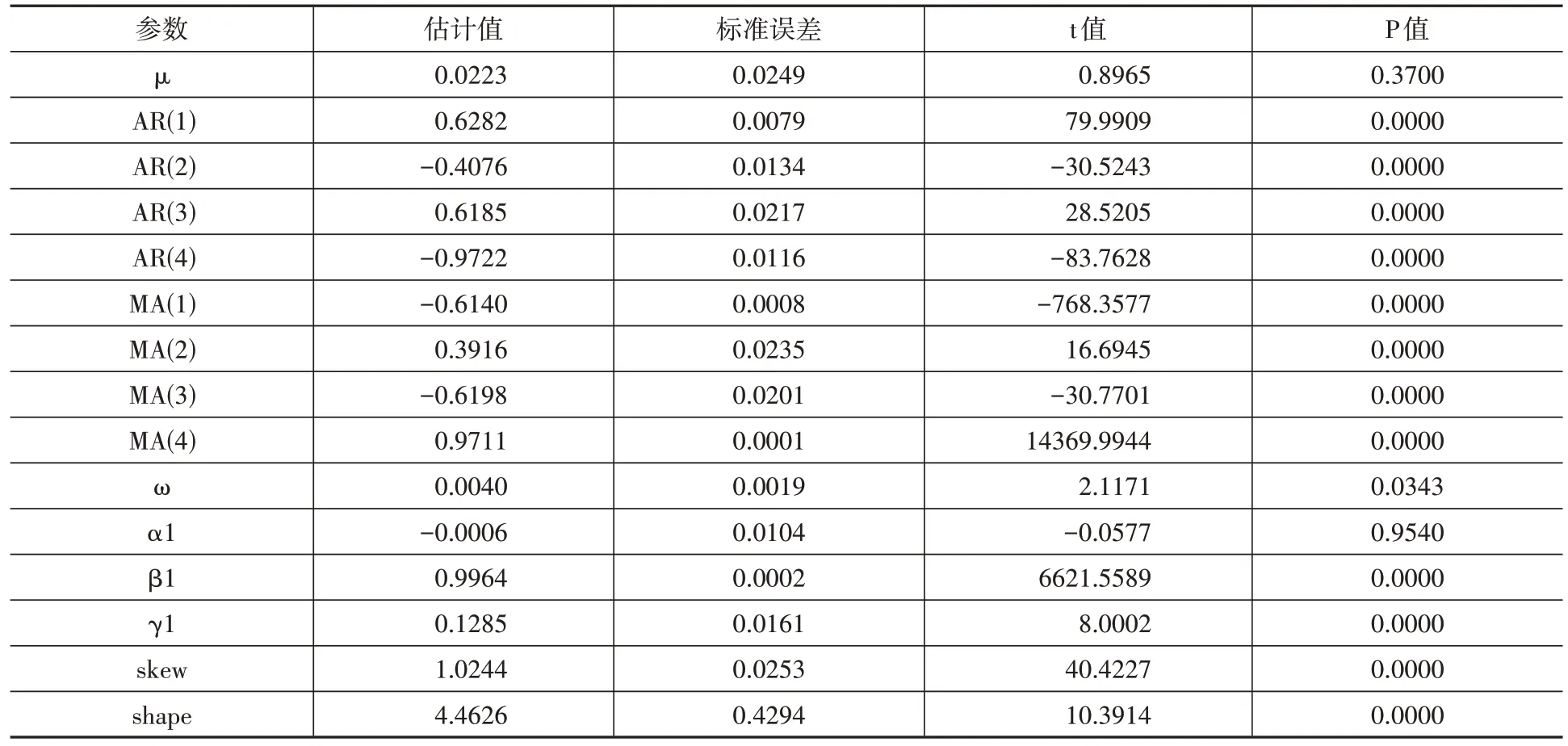
表4 金融行业ARMA(4,4)-EGARCH(1,1)-sstd模型估计结果

表5 ARMA-GARCH 模型度量及回测结果

3.基于GARCH-QRNN-POT 模型的VaR

用GARCH-QRNN 模型计算正常情况下两行业的VaR 值。将经过ARMA-GARCH 模型过滤的波动率序列输入初始神经网络。通常交易所连续交易5 天，设置输入变量的滞后阶数I= 5，隐藏层转换函数设为Sigmoid 函数，输出层转换函数设为线性函数，根据代价函数最小原则确定隐藏层节点数及权值衰减项系数，结果见表6。

表6 QRNN模型节点数及权值衰减项系数确定

将确定的节点数及权值衰减项系数代入QRNN 模型，训练神经网络，确定隐藏层和输出层的权重及偏置。

代入测试集数据，计算5%分位数，从而得到正常情况下的VaR 值并进行回测检验，结果如表7 所示。

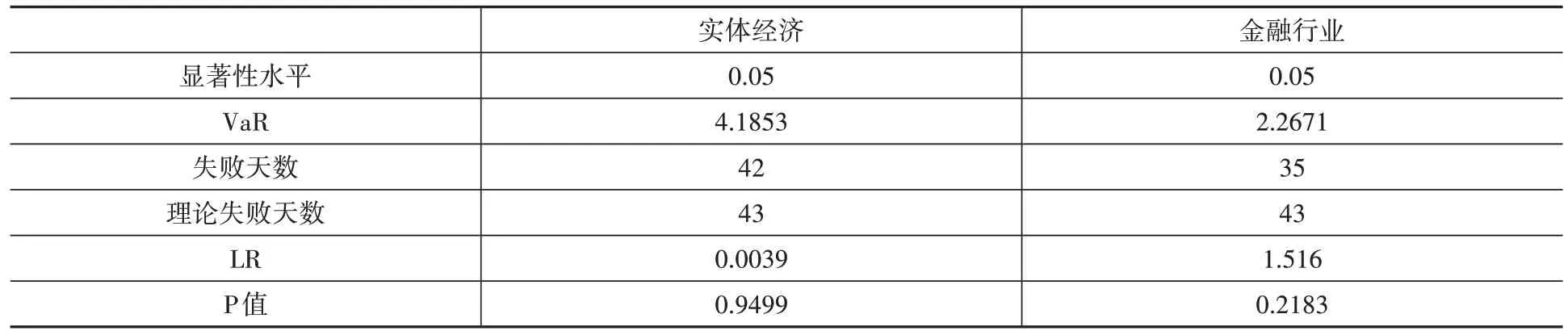
表7 GARCH-QRNN 模型度量及回测结果

将标准化后的分位数残差代入POT 模型，根据式（22）得到极端情况下的VaR 值，提高了模型对于极端情况的预测能力。原因在于，POT 模型是对极端值数据进行建模；但随着极端程度的加深（如：显著性水平由1% 至0.1%），POT 模型的可用数据会越来越少，在一定程度上影响模型的拟合效果，模型（26）的重要性体现在：实现了从正常情况到极端情况的转换，同时使得POT 模型的可用数据大幅扩展，两模型相结合更加贴近现实情况。建立基于广义帕累托分布的POT 模型最关键的是阈值u 的选择，选择最经典的Hill 统计量估计法并结合超额均值函数图确定阈值。

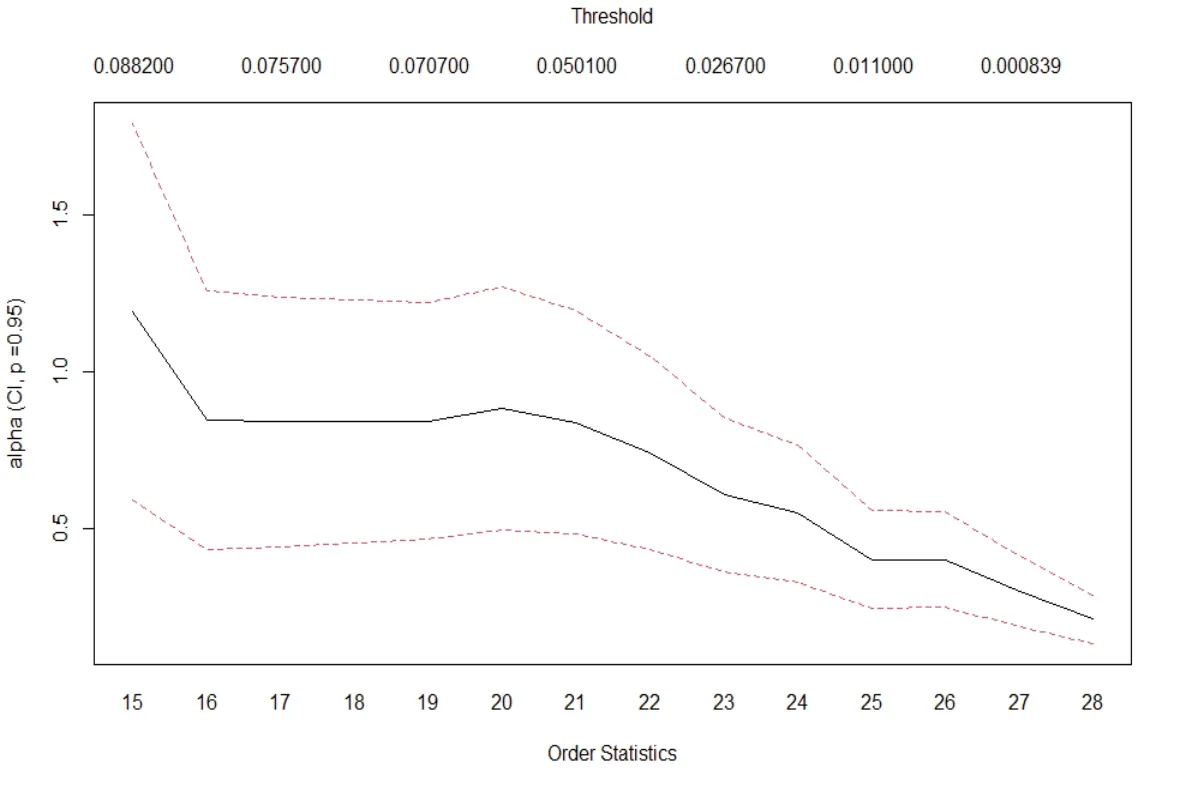
图1 实体经济POT模型Hill图

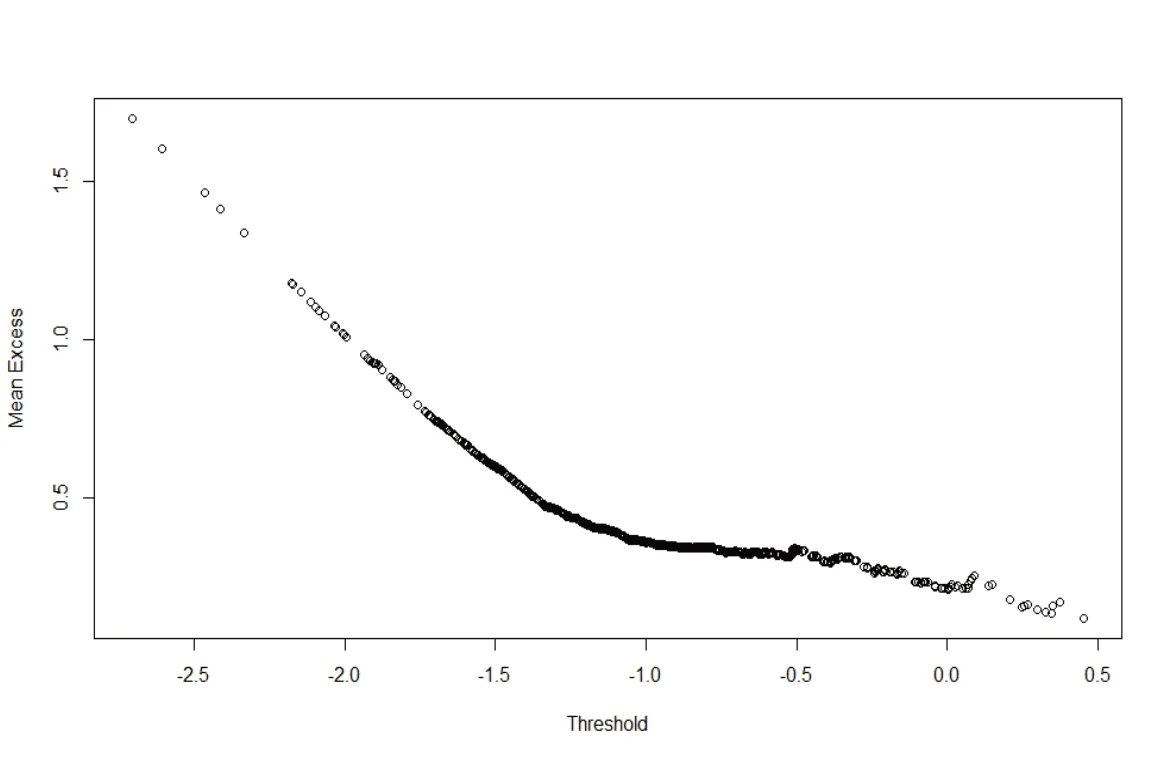
图2 实体经济POT模型超额均值函数图

Hill 统计量估计法选取阈值的要点在于选取Hill 统计量变得平稳时的阈值；超额均值函数图选取阈值的要点在于选取超额均值函数开始呈现近似线性时的点，因此，实体经济选取阈值0.13、金融行业选取阈值0.15 较为合理。拟合POT 模型得到尺度参数β和形状参数ζ的估计结果。

实体经济指数尾部的拟合诊断图见图5，金融行业指数尾部的拟合诊断图见图6，两指数的超额分布图和尾部分布图的点基本在一条线上，残差QQ 图近似线性，说明广义帕累托分布的POT 模型进行尾部风险的度量拟合效果较好。

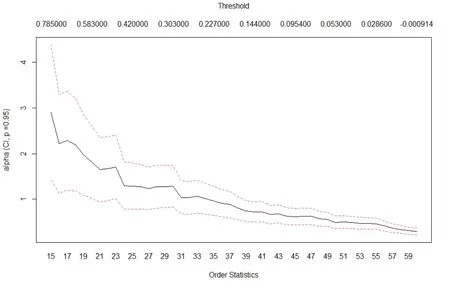
图3 金融行业POT模型Hill图

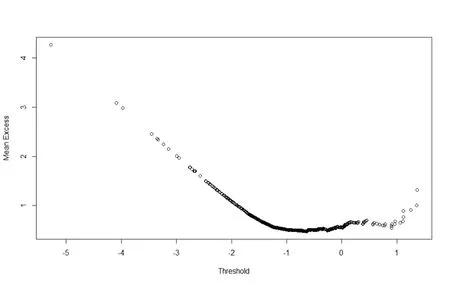
图4 金融行业POT模型超额均值函数图

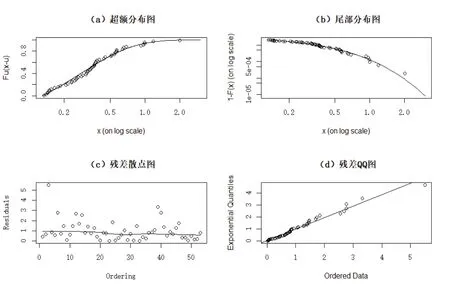
图5 实体经济指数尾部拟合诊断图

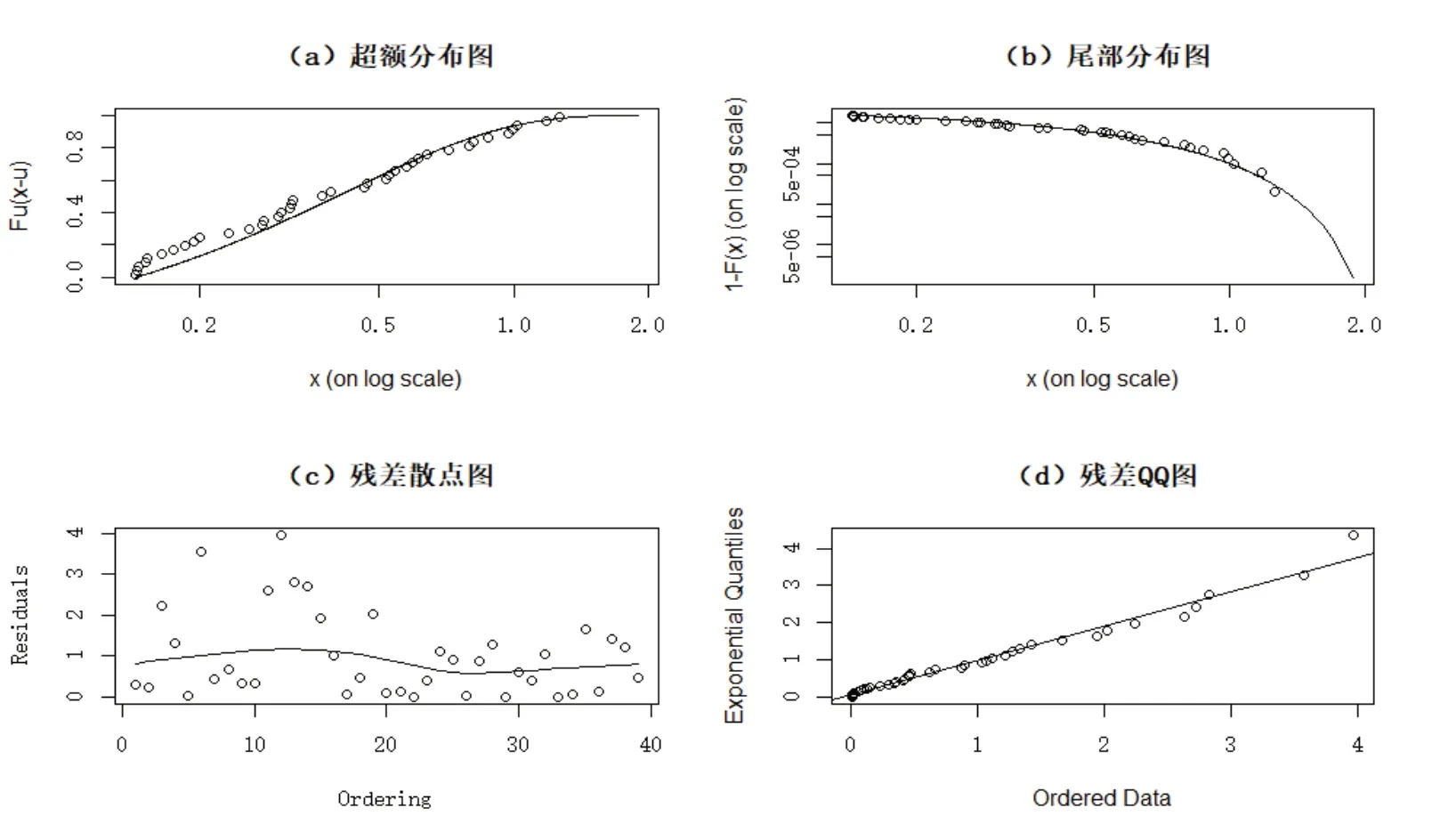
图6 金融行业指数尾部拟合诊断图

根据模型（22）计算分位数Qzt(1 -τ1)，根据模型（26）计算极端情况下的VaR 值，并在测试集上进行回测检验，结果如表9 所示。

表8 POT模型参数估计结果

表9 GARCH-QRNN-POT 模型度量及回测结果

通过对比ARMA-GARCH 模型和GARCHQRNN-POT 模型结果（表5、表7 和表9）可以看出，对于实体经济的风险测度，ARMA-EGARCH模型在5%和1%的显著性水平上估计的VaR 值均未能通过回测检验，且低估了实体经济的风险；而引入神经网络分位数回归和极值理论的GARCH-QRNN-POT 模型在5%和1%的显著性水平下估计的VaR 值均通过了回测检验，有效提高了模型的风险度量能力。对于金融行业的风险测度，两模型在5% 的显著性水平上估计的VaR值均通过了回测检验，表现较好；但ARMAGARCH 模型对于极端风险的度量能力较差，在拒绝域的边缘，并低估了金融行业的风险，而GARCH-QRNN-POT 模型对于尾部风险的测度更加准确，对极端风险的度量能力明显优于ARMA-GARCH 模型，后续估计两行业间风险溢出效应时使用GARCH-QRNN-POT 模型。在95%置信水平下，实体经济的VaR 值为4.1853，远大于金融行业的2.2671；在99% 置信水平下，实体经济的VaR 值为6.6838，同样远大于金融行业的3.5172，这说明实体经济的风险远大于金融行业；随着置信水平的上升，实体经济的风险急剧增加。

（三）系统性风险溢出效应

根据模型（5）、模型（6）和模型（7）计算Co-VaR、ΔCoVaR 和%CoVaR，衡量两行业的极端风险溢出方向和效应大小，结果如表10—11 所示。两行业的增量条件在险价值ΔCoVaR 同号，说明两行业间存在双向的风险溢出，从侧面佐证了格兰杰因果检验的结论。其中，在95%的置信水平下，实体经济对金融行业的溢出强度为44.12%，而金融对实体行业的溢出强度为72.99%，这说明在正常情况下一旦金融行业发生风险事件，会迅速波及实体经济，实体经济的风险将急剧增加，且强度大于实体经济对金融业的风险溢出强度；在99%的置信水平下，实体经济对金融行业的溢出强度大幅上涨增至69.66%，而金融对实体行业的溢出强度相对较小增加至82.49%。当更严重的极端情况发生时，实体经济对金融的波及程度将急剧上升，风险扩散的增长速度将远大于金融行业对实体经济风险扩散的增长速度。

表10 实体经济与金融行业间极端风险溢出(τ = 0.05)

表11 实体经济与金融行业间极端风险溢出(τ = 0.01)

五、结论与建议

本文将GARCH 族模型与QRNN 模型、极值理论中的POT 模型结合起来，构建GARCHQRNN-POT 模型，用以度量不同情况下实体经济与金融产业的系统性风险及二者间的风险溢出效应。

首先，对实体经济与金融行业的收益率序列构建ARMA-GARCH 模型；其次，对波动率序列构建QRNN 模型；再次，对标准化的残差序列构建POT 模型，进行极值理论的分析并估计广义帕累托分布参数；继次，计算不同情况下的VaR 值，并与常用的ARMA-GARCH 模型计算的VaR 值进行对比，性能比较方法采用Kupiec 失败率检验法；最后，通过条件在险价值CoVaR 度量实体经济与金融行业之间的风险溢出方向与强度。

GARCH 模型检验结果显示：对称的GARCH模型足以刻画Wind 金融一级行业指数的ARCH效应。在险价值VaR 显示：实体经济具有较高的风险，远高于金融行业。回测检验的结果表明：两情形下ARMA-GARCH 族模型均会低估风险水平，不能或刚刚通过回测检验；而GARCHQRNN-POT 模型的表现明显优于ARMAGARCH 族模型。原因在于：金融业与实体经济间风险的复杂关系是非线性的，且ARMAGARCH 族模型对极端数据的处理能力不足。而QRNN 模型在刻画复杂关系时更具优势；POT 模型善于处理极端数据，但直接使用POT 模型的表现仍不佳，主要是总数据量和有效数据量较小导致，进行扩充或转化会使POT 模型在经济领域的表现更佳。

格兰杰因果检验结果和增量条件在险价值ΔCoVaR 均表明：实体经济与金融行业间存在双向的风险溢出。金融行业对实体经济的溢出强度在正常情况和极端情况下均大于实体经济对金融业的溢出强度但随着极端情况的加剧，实体经济对金融的波及程度将急剧上升，风险扩散的增长速度远大于金融行业对实体经济风险扩散的增长速度。

基于以上结论，本文提出如下建议：

第一，金融业与实体经济的系统性风险水平是非线性变化的。随着情况的加剧，应适时引入相关模型，而非一成不变的，仅使用单一模型测度不同情况下系统性风险会使得测度结果不准确，甚至是无效的。

第二，实体经济与金融行业紧密相连，在当今这个行业交叉发展的时代背景下，应对整个实体经济与金融行业间的风险溢出给予更多的关注和研究，不仅是房地产行业与银行业。局部的风险溢出关系不足以满足如今的需要，需要从整体关联性的角度对系统性风险溢出效应进行拓展。

第三，实体行业的风险扩散程度是动态变化的，对于实体行业要有针对性的给予关注，如日常消费、房地产等与我们息息相关的且必需的行业，控制其风险扩散；而对于金融行业要经常性的关注，加强对金融业的监管和政策引导，并及时向社会传递监管信息，包括对实体行业的信贷结构信息、各机构系统重要性动态排名信息、系统性风险动态评估结果等。

第四，将实体行业的风险防控纳入到我国系统性风险监管体系中。密切关注实体行业经营状况，把控其风险水平，使其风险防控更加合理有效；同时，积极引导实体行业正确合理地使用财务杠杆，切实加强其抵抗风险的能力。

第五，健全我国金融监管体系，提升监管效率与力度。明确各监管机构职责，尤其需要注重监管机构间的协调机制，避免监管空置和监管重叠的情况出现。