基于CTPN的智能车间双资源调度研究

朱天一,吕雅琼,张树柱

(1.武汉理工大学 交通物流工程学院,湖北 武汉 430070;2.浙江财经大学 信息管理与人工智能学院,浙江 杭州 310018)

智能制造要求传统车间提高自动化水平,加快物料流转,降低生产成本,提高经济效益。在工件的排程问题中,刘蓉等[1]针对具有批处理的柔性制造车间,提出了改进遗传算法并进行有效调度。AGV的调度极大地影响了智能车间加工效率,范媛等[2]在多AGV的仓储空间里完成了车辆的合理配置。多AGV的智能车间的系统性能优化,即是对具有更高计算复杂度的AGV与机器联合调度问题的方案进行优化。

近年来,学者就AGV与机器集成调度展开研究,针对机器资源与路径资源的分配,遗传算法[3]、粒子群算法[4-5]、差分进化算法[6]等进化算法被证明是行之有效的,并且可以结合启发规则[7]。但这些研究假设AGV的运行速度可变,不能完成对系统的实时控制。

Petri网(PN)的形式化语言适用于大型FMS中经常出现的异步触发、阻塞、并发和其他动态行为[8]。Petri网构建系统模型获得初始状态,通过状态-变迁-状态的形式获得AGV生产系统中的全部解空间。Petri网模型可通过遗传等进化算法[9-10]获得确定问题下的最优变迁序列,实现最优调度决策。在AGV路径规划问题上,李圣男等[11]采用分解子网方式实现AGV的无冲突运行。基于Petri网的方法不仅可以在机器调度上具备优势,还可以获得每个时间点AGV的运行状态,以便进一步优化系统。因此,笔者将采用基于Petri网的机器调度与路径规划两阶段求解方法,采用有色时间Petri网缩小网络规模,并通过遗传算法与A*算法实现调度方案。

1 问题描述

具有AGV系统的智能生产车间联合调度优化问题通常可以描述为:已知工件集J={J1,J2,…,JN},M={M1,M2,…,MM},AGV集R={R1,R2,…,RR},每个工件需要操作OPi={Pi1,Pi2,…,Pi|OPi|},|OPi|为工件i的操作数量,i∈J。假设每个工序的加工机器已知,且工件在不同机器上加工需要AGV配送,其运输时间由选择的路线决定,要求完成所有工件的加工任务的完工时间最小。

为了使研究问题更为完备,做出以下假设:①初始时刻所有AGV与机器可用,所有加工零件存放于装卸站;②AGV运输速度恒定且装卸时间不计;③机器的坐标已知,体积忽略不计,所有AGV的初始位置已知。

2 Petri网建模

2.1 Petri网模型

模型分为生产与物流两部分,需要通过资源库所将不同的子模型进行链接。轨道模型将节点变为库所,AGV在节点上的移动通过变迁实现。加工过程模型则以变迁映射一个加工行为。对只有4个节点、2台加工机器、1辆AGV的场景,完成2件工件加工的联合模型如图1所示,该模型存在19个库所、20个变迁,因此有必要对其进行简化。

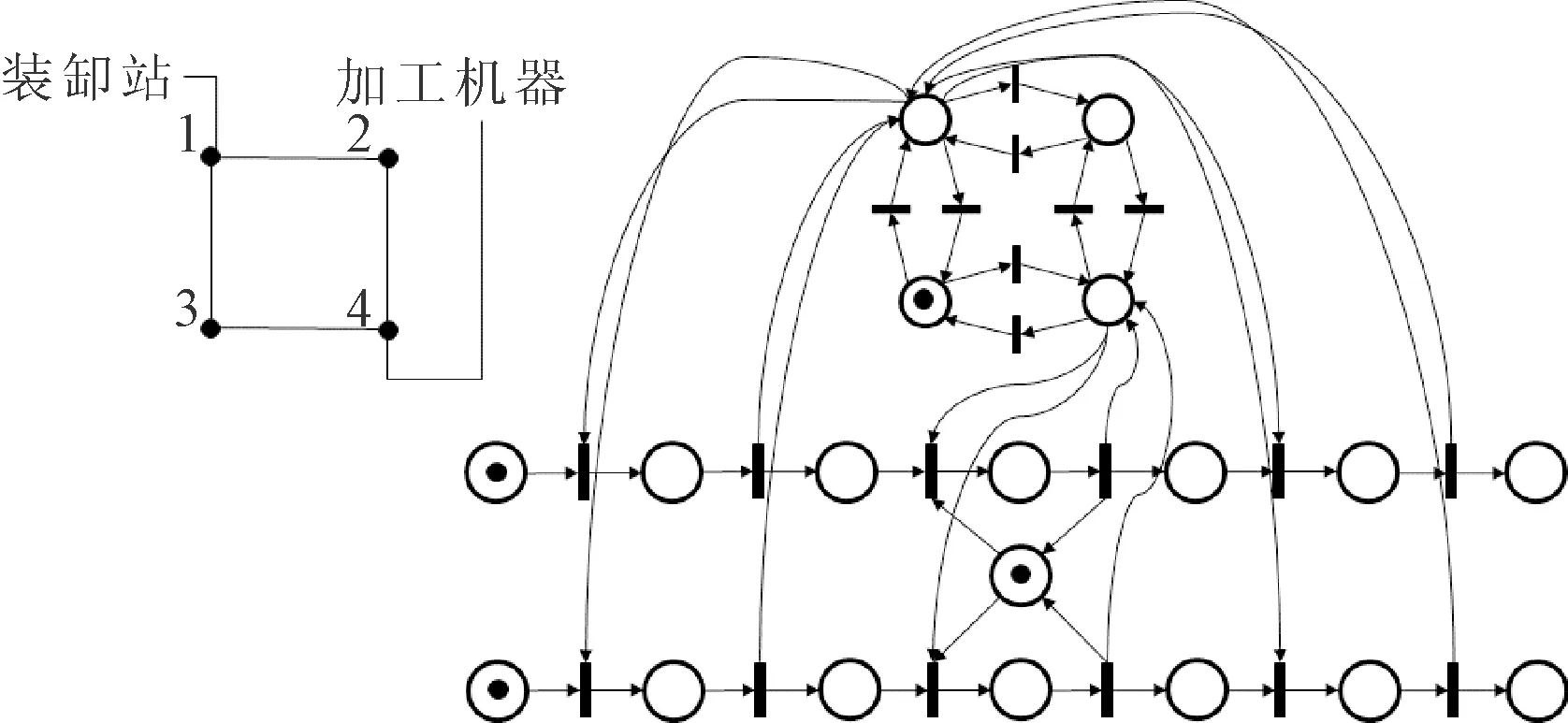
图1 机器与AGV联合调度及建模

2.2 有色时间Petri网

为了降低Petri网模型规模,分别对零件加工过程与AGV系统展开语义拓展。拓展的Petri网语义包括T-变迁、P-变迁、C-变迁、C-库所和D-库所[12],详细解释如表1所示。采用拓展语义构建基本模型,对工件活动分别构建加工过程模型和运输过程模型,基本结构如图2(a)和图2(b)所示,对AGV的活动进行建模,基本结构如图2(c)所示。

表1 拓展Petri网图形解释

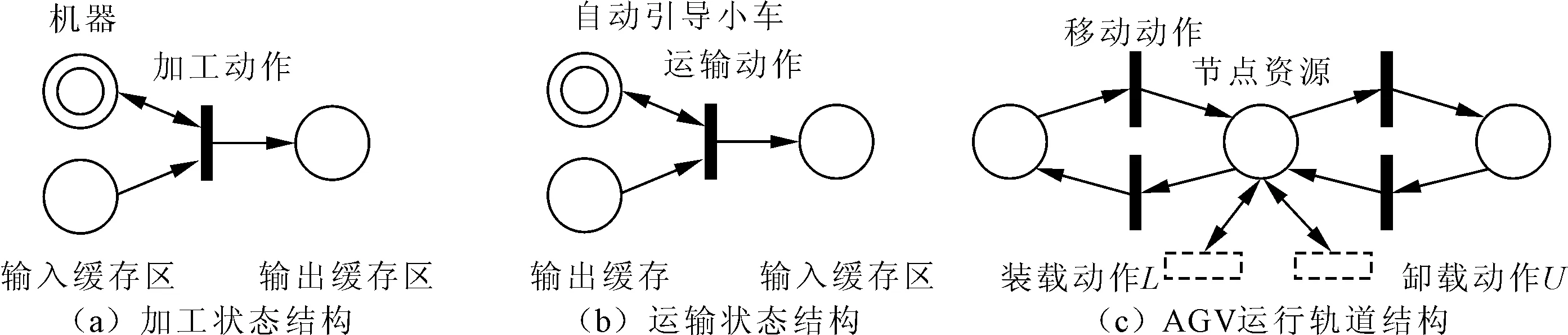
图2 拓展语义在基本结构中的应用

3 算例分析

3.1 算例描述

具有2辆AGV的FMS调度车间需要6台机器完成6种工件的加工,加工车间场景布局如图3所示,其中Mi表示具有输入缓冲区和输出缓冲区的加工机器;AGV初始位置在停靠站,编号为0,其通过每条边所需要时间为1;UL为装载站,零件的原材料与产成品的存放处。工件的加工时间如表2所示。

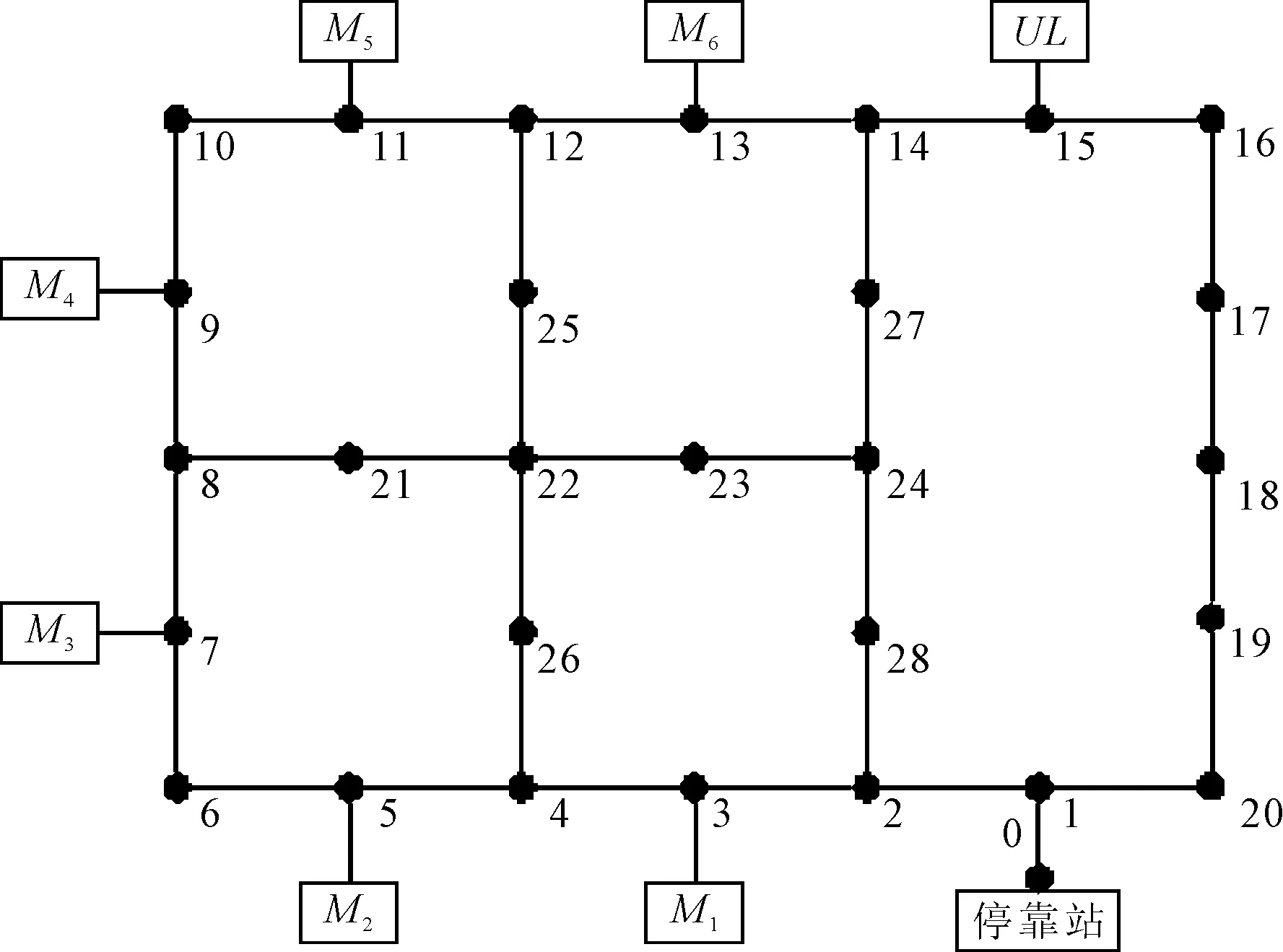
图3 车间布局图

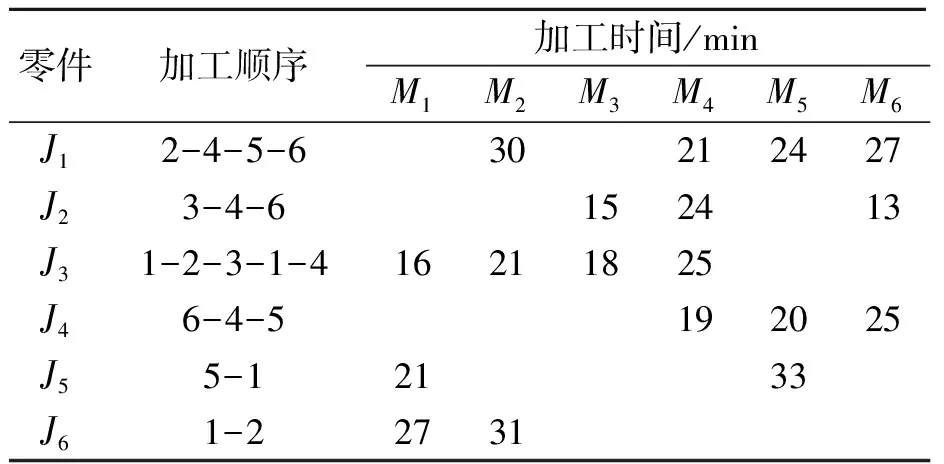
表2 工件的加工时间

3.2 面向算例的CTPN模型

简化后的CTPN联合调度模型如图4所示。其中,加工流程考虑AGV空载运行、AGV负载运输、机器加工3类具体动作,其中JIi,j、JOi,j分别表示工件i在机器j的输入与输出缓存区,ULi、Ti,j,k、Pi,j分别表示工件i的装卸动作、由j配送至k的动作、在机器j加工的动作。每个资源以不同种类颜色存在于库所中,如UL中存在6种颜色的令牌,颜色标识的解释如表3所示。

表3 加工模型颜色描述

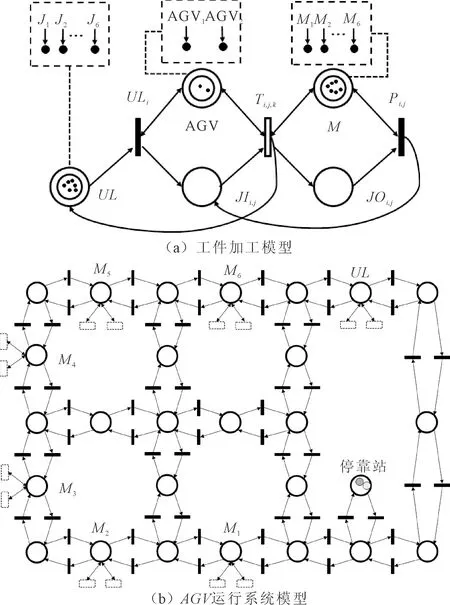
图4 加工过程的CTPN模型

对案例的求解则是在CTPN模型中确定一组(Ti,j,k,Pi,j)构成的变迁序列,表示配送和加工的顺序。当Pi,j为工件i的第一道工序时,该动作变为(Ti,O,UL,Ti,UL,k,Pi,1),其中Ti,O,UL为AGV从当前节点前往装卸站UL的动作,Ti,UL,k表示AGV从UL到目标机器k的动作。AGV与机器的占用由函数Φ确定,Φ(Ri)=1表示机器Mi被占用,否则为空闲;同理,Φ(Ri)=1表示AGV集中Ri被占用,否则为空闲。求得完成所有的变迁动作所需要的时间最小,即为最佳任务分配方案。

3.3 实验分析

采用遗传算法与A*的联合算法求解算例,并与禁忌搜索算法进行对比分析。对于遗传算法,将每个染色体编码为加工序列,生成配送任务,再通过A*算法中求解每个AGV的最短路径。测试使用Python作为开发工具,设置遗传算法的种群规模为100,迭代次数为100次,交叉概率为0.6,变异概率为0.1。每个染色体为一个任务列表,传入运输模型,通过A*算法依次计算完成每个任务的时间,使总任务完工时间最小。

算法优化曲线如图5所示,纵坐标为每一代的最短完工时间,横坐标为迭代步数。从图5可以看出,基于遗传与A*的联合算法在第20代时开始收敛,而禁忌搜索算法则需要迭代90代才开始收敛。为了进一步说明所提算法的可行性,统计了10次计算结果进行对比,具体结果如表4所示,可以看出笔者算法与禁忌搜索算法皆可以获得最优调度方案,但笔者算法所需的平均计算时间更短。

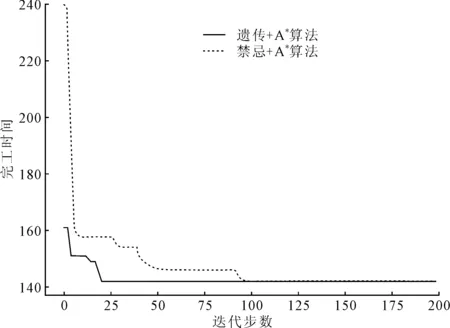
图5 算法优化曲线对比

表4 实验结果对比

在选择的案例中,获得的调度结果如图6和图7所示。图6为AGV运行状态图,表示每个时间点每辆AGV所在的位置。图7为联合调度甘特图,每个有色矩形表示加工过程或配送过程,颜色代表了这一时间段内机器与AGV所携带的工件类型。

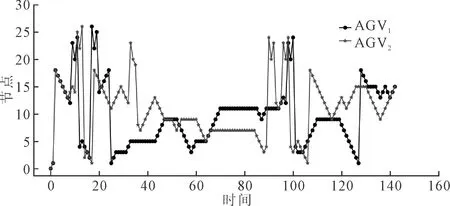
图6 AGV运行状态图

图7 联合调度甘特图

4 结论

(1)提出了一种基于遗传算法与A*优化的CTPN模型,通过求解最优变迁序列获得联合调度决策。基于遗传算法与A*的联合优化算法在双资源调度问题上具备优势,收敛速度快,计算结果准确,且所提方法可以观测AGV的运行状态,为基于AGV的多目标优化奠定基础。

(2)Petri网图形化的表达方式能够直观反映车间生产活动中的并发、冲突行为。

(3)所提出的建模方法有效缩减了普通Petri网表征系统时的规模,可读性大大加强,调度结果准确,可作为一种可靠的双资源调度优化模型。

(4)尽管算例依据提出的方法得到了有效调度方案,但仍有很多方面值得拓展改进。研究中算例规模较小,且忽略了AGV彼此之间的影响,在未来的研究中将扩大问题规模,并具体考虑更符合实际场景中的多AGV路径冲突、抢占、死锁等约束。