课后习题与新课程标准一致性分析
——以初中数学人教版教科书“有理数”为例
邓 希 马廷福
(宁夏师范学院数学与计算机科学学院,宁夏 固原 756000)
马廷福(1981.1-),男,宁夏同心人,博士,教授,从事计算流体力学、数据分析和挖掘相关的学术研究.
1 研究工具
由于韦伯模式研究维度丰富,取样方便,有临界指标,能够提供详细、精确的定量研究结果,所以本文选择韦伯模式作为一致性研究工具.它主要是将课程标准的内容分为三个层级,即“学习领域”“主题目标”和“具体目标”,三者之间组成“金字塔”一样的目标层级体系.每个具体目标设置相应的知识水平,即回忆(Recall)、技能或概念(Skil/Concept)、策略性思维(Strategic Thinking)和拓展性思维(ExtendedThinking)四个级别的知识水平.这仅涉及我国三维目标中知识与技能这一维度,不涉及过程与方法、情感态度与价值观两方面的相关课标要求.并且为了结合我国课标实际需求,将第三级具体目标应达到的认知水平本土化以下四个等级.为后续研究方便,分别编码为A、B、C、D.具体如表1所示.

表1 认知水平划分
2 课程标准及习题编码
2.1 编码人员的选择
为了使课后习题的编码具有有效性,所以本文选择3名一线教师和3名学科教学(数学)的研究生对人教版初中数学教科书《有理数》这一模块的课后习题进行独立编码.对于编码结果不一致的题目,可以相互交流讨论,最后确定编码结果.
2.2 课程标准中内容要求的编码
由于新课标中有些内容标准同时含有几个不同深度水平的行为动词.针对此情况,在对内容标准中每个主题下的每一条内容标准进行编码时,要按行为动词水平的不同等级进行进一步的拆分成若干详细目标,例如该项内容标准:“理解平均数、中位数、众数的意义,能计算中位数、众数、加权平均数,知道它们是对数据集中趋势的描述.”它包含三个程度不同的行为动词,因此编码时得把这一项内容标准拆分为三个不同的详细标准.
本研究内容标准编码序号采用“学习领域、学习主题、详细标准”的格式进行排序.例如,第一个学习领域“数与式”,编码为1,其第一个学习主题“有理数”编码为1.1,第一个学习主题中的一条详细标准则编码为1.1.1.
结合以上两点,具体编码结果如表2.
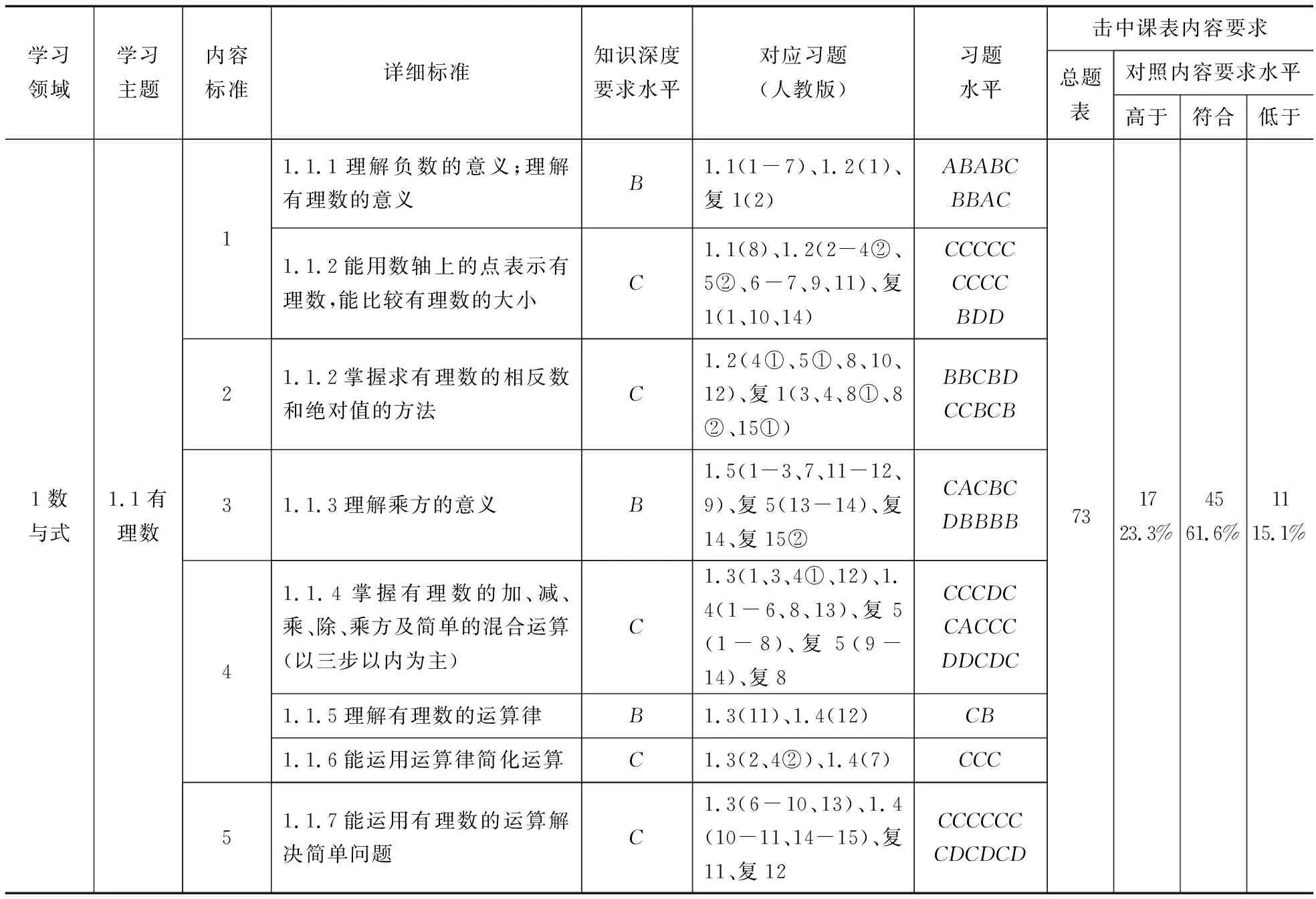
表2 有理数课后习题与课程标准的一致性分析
2.3 习题选取及编码
考虑到部分课后习题所考察的知识点在两个或两个以上,因此作以下三点说明:
(1)若课后习题所考察的不是同一主题的知识点,则只编码本章节所属主题相关知识点;
(2)若要对1.1节的课后习题进行编码,1.1节中的第一题就表示为1.1(1);若要对复习题1中的第一题进行编码,则将其编码为复1(1),以此类推.
(3)某题中有两小问及以上且击中的是同一主题中不同详细标准的知识点,则需将其分开编码,例如1.2节中的第四题,它包含两小题且击中的不是同一详细标准的内容,因此分别编码为1.2(4①)、1.2(4②).相反,若某题中有两小问及以上且涉及的是同一主题中同一详细标准的知识,但其考察的深度不同,也需将其分开编码.具体编码结果如表2.
3 课后习题与课程标准的一致性分析
3.1 知识种类的一致性
知识种类一致性是用来判断习题所考察的知识点与新课标学习主题中详细目标的要求是否相一致.当课后习题至少6次“击中”详细目标的内容,知识种类一致性才可以接受.由表2可知“有理数”主题对应的习题共73道,远远超过了6道.所以从主题层面上看,课程标准与课后习题的一致性程度较高;从内容标准层面上看,第1,2,3,4,5条的内容标准分别有21,10,10,20,12道习题,故5条内容要求与课程标准的一致性程度也较高.
3.2 知识深度的一致性
知识深度的一致性,它是指习题所考察的深度与内容标准中所要求学生达到的认知水平是否相对应.当课后习题所考察的深度至少有50%击中新课标中相对应主题下具体目标所要求的认知水平,则认为两者在知识深度这一维度达到了一致性.由表二可知,在主题层面上,共有61.6%的习题符合课程标准所要求的深度水平.在内容标准层面上,第1,2,3,4,5内容标准符合课标的知识深度百分比分别为61.9%,40%,50%,70%,75%.所以1,2,4,5内容标准的一致性程度可接受.
3.3 知识广度的一致性
知识广度一致性是用来判断习题击中所对应学习领域中具体目标的范围,若范围大于等于50%,则两者在知识广度这一维度达到了一致性.由表2可知,内容标准数共5条,击中5条;在详细标准层面上共8条,击中8条,命中率100%,所以在内容标准和详细标准层面上都达到了一致性可接受水平.
4 结论与建议
4.1 结论
通过上述研究,得出课后习题在知识种类、知识广度和知识分布平衡性方面都与新课标有比较好的一致性.部分习题在知识深度内容标准层面上的一致性程度还没达到可接受的水平,这说明课后习题的编制几乎是符合新课标的要求,对于没有达到的课标的习题,需要改进和完善.
4.2建议
4.2.1 教科书编写应合理设置其课后习题的难易难度
通过对韦伯模式中知识深度这一维度的研究,发现部分课后习题所考察的难度没有达到新课标的要求.也就是说,这部分习题不能很好地检验学生的能力.这就对教科书的编写者提出了要求,他们需要准确把握教科书与新课标的一致性,使教科书的编写符合新课标的要求.只有这样,课后习题才能起到检验和巩固知识的作用.
4.2.2 教师要准确把握课程标准的内容
新课标作为政策性文件,需要教师在教学中有效落实才能发挥其价值性.而有效落实的前提则是教师准确把握课程标准的内容.只有这样,教师的教学才有明确的目标和方向,并且在教学时会针对教科书中不足的地方进行补充和完善,从而提高学生的学业质量水平和培养学生独立学习的能力.
4.2.3 教师教学要有灵活性
教师在课堂教学的内容既要符合新课标的要求,又要满足学生的需要,如果过度追求两者的一致性,则可能不利于学生的身心发展.因此教师的教学不能单一死板、一成不变地遵循新课标的要求,而应该灵活、随机应变,比如可以编制课外习题,寻找新课标一致性与学生需要的平衡点,这既符合了新课标的要求,又能满足学生学习的需要.

