基于匹配度和谱聚类的知识推荐研究

张建华, 郭启迪, 曹子傲, 刘艺琳

(郑州大学 管理学院 河南 郑州 450001)

0 引言

知识推荐作为知识服务组织主要的服务方式,其将知识及时、精准地对接需求,有助于知识价值的实现与增值。近年来,关于知识推荐的研究主要集中在图书馆等特定场景,也有部分学者尝试构建全环境适用的知识推荐系统。Yin等[1]从知识与任务之间的关联度、基于反馈的个人经验、设计师的集体经验以及基于遗忘曲线的知识需求度四个维度对知识进行评分,并根据评分获得知识推荐列表进行知识推荐。蔡之玲等[2]以DKN算法为基础,构建了档案知识推荐系统。臧振春等[3]从产品的属性与用户需求匹配的角度出发,利用Vague集构建模型计算相似度,完成针对用户需求的知识匹配并推荐结果。

知识推荐算法主要包括协同过滤算法、基于内容的主题推荐算法、基于模型的推荐算法和基于混合方式的推荐算法[4]。在推荐算法中,协同过滤算法是应用较为广泛的一种算法,它通过对已知用户和推荐系统的交互结果与用户的偏好情况进行分析,从而对类似用户进行推荐。近年来,很多针对协同过滤算法的研究将其与新兴算法相结合,对协同过滤算法进行优化。王永贵等[5]利用狼群算法的遍历特点,将狼群算法、FCM算法与协同过滤算法进行结合,从而提高协同过滤算法的准确性。黄敏等[6]将注意力机制引入基于卷积神经网络耦合的协同过滤模型中,提高了协同过滤算法的推荐性能。与此同时,一些研究聚焦于特定情境下的协同过滤算法。卢竹兵等[7]将情感分析和协同过滤遗忘曲线相结合,从时间和情感角度改进协同过滤推荐算法,提高了推荐算法的准确率。

除此之外,科研人员在相似度计算方面取得了一些新成果,主要包括以下类型:① 通过融合不同的相似度计算方法进行计算。Wang等[8]对基于记忆的协同过滤进行研究,提出一种基于评级和结构化的相似性度量的协同过滤算法,从相似度计算方面对协同过滤算法进行改进。Liu等[9]提出一种结合均方差、Jaccard相似度和用户行为的全局偏好的相似度计算方法,在一定程度上解决了用户冷启动问题。② 通过融合不同属性因素形成新的相似度计算方法。金志刚等[10]通过构建用户-项目评分矩阵,并考虑属性对用户评分的影响构建映射关系,生成用户-属性矩阵,再根据上述两个矩阵形成相似度计算矩阵,进而计算出用户间的相似度,并根据KNN算法生成推荐列表。武建新等[11]以Jaccard相关系数为基础,将用户的显隐兴趣、奇异值、评分差异等因素融合进相似度计算中,并考虑时间权重,提出一种融合用户评分与显隐兴趣相似度的协同过滤算法。杨辰等[12]利用K-means算法,分别以用户和项目为聚类对象进行聚类,并将聚类形成的簇与KNN算法和协同过滤算法相结合进行推荐,能够更深层次地表征用户偏好。申艳梅等[13]提出将用户年龄、性别、职业等属性差异度与Pearson相似度相结合,形成用户层面的综合相似度,再结合项目时间相似度和项目属性相似度形成项目层面的综合相似度,以此提升推荐系统的精确性和时间效率。

综上,关于协同过滤推荐算法的研究成果较为丰硕,该类算法已广泛应用于医药、传统制造等具体领域。不过,现有的知识推荐相关研究在推荐结果的计算层面更多着眼于对知识之间不同种类条件相似度的研究,偏向于对隐性知识之间外在相似性的分析,而忽略了对隐性知识之间内在关联性的研究。基于已有研究成果,本文以融合知识评分相似度和属性关联度的知识匹配度来衡量知识间的匹配关系,并利用谱聚类算法对知识空间进行压缩以降低遍历时耗,最后以同簇内知识项匹配度和已有评分信息进行评分预测,并据此锁定推荐范畴。利用Movielens数据集对所提出的知识推荐算法进行仿真模拟分析,并与既有推荐算法进行了对比。

1 相关概念

1.1 协同过滤算法

协同过滤算法是出现最早、应用最广的推荐算法。它通过分析用户兴趣,找到与该用户相似的用户群体,并将这些用户对某一个项目的评价信息进行综合化处理,形成一个对用户和特定项目的偏好进行预测的系统。

协同过滤算法从协同对象角度可分为基于用户的协同过滤算法和基于项目的协同过滤算法。其中,基于用户的协同过滤算法通过计算获取与被推荐用户最为相似的用户群体,并根据其偏好进行推荐;基于项目的协同过滤算法基于用户现有偏好情况,求出与用户满意项目最为相似的项目,并将其作为推荐项目进行推荐。本文采用基于项目的协同过滤算法,依据用户对知识项的评分喜好以及知识之间的匹配程度进行推荐。

1.2 知识视图相似度

根据知识本身所具有的不同特征和不同属性,可对知识项目或者知识属性之间的相似度进行计算,并基于此得到衡量知识之间相似性的视图相似度。测度知识视图相似度的常用方法有余弦相似度、欧氏距离相似度、Pearson相似度、Jaccard相似度等。

现有的协同过滤算法在相似度计算方面主要对权重因子进行创新。Bobadilla等[14]提出了结合均方差和Jaccard相似度的综合相似度计算方法,提升了推荐结果的准确性。武森等[15]以综合相似度为基础,提出一种稀疏余弦相似度计算方法,弥补了传统相似度计算方法对稀疏数据处理的不足。

根据用户-知识的评分信息构造评分矩阵Rm×n,如表1所示。其中:m为用户数;n为知识项数。

采用余弦相似度计算知识之间的视图相似度,公式为

(1)

其中:ki和kj分别为知识项第i项和第j项,即用户-知识评分矩阵第i、j列数据构成的列向量。

表1 用户-知识评分矩阵Table 1 User-knowledge scoring matrix

1.3 知识关联度

既有相关成果主要聚焦知识之间的相似性,而忽视了知识之间的内在关联性。关联性影响推荐结果对用户需求的满足程度,且在实践中存在知识间“高相似低关联”与“高关联低相似”的情况。鉴于此,本文基于Apriori关联规则算法,挖掘知识属性之间的关联规则,以进一步改进推荐效果。算法步骤如下。

Step 1 以知识项与知识属性作为两个变量,按式(2)填充矩阵的横、纵向量,结果如表2所示。其中:n为知识项数;p为知识属性项数;aij取值满足

(2)

表2 知识-属性矩阵Table 2 Knowledge-attribute matrix

Step 2 遍历知识-属性矩阵,对知识属性值所出现的次数进行计数,得到频繁一项集。

Step 3 再次遍历知识-属性矩阵,设置最小支持度阈值σ,并计算同属性值的频繁二项集。

Step 4 计算频繁二项集的置信度conf,并建立知识-属性关联度矩阵,将空缺值填为0。

Step 5 计算知识项之间的关联度,公式为

(3)

1.4 谱聚类算法

谱聚类算法作为近几年新兴的聚类算法,除机器学习和数据挖掘领域之外,已被广泛应用于交通运输的路网划分[16]、脑功能精细分区[17]等领域。谱聚类是以图论为基础的算法,拥有样本形状敏感度低、收敛于最优解、对高维数据支持较好等特点。谱聚类将样本和样本相似度生成无向图,样本作为图中的点,样本相似度作为连接样本之间的边,相似度的大小则为边的权重[18]。如此,在无向图中便可将聚类问题转化为对图的划分问题。应用最广泛的无向图划分准则包括:最小割集准则、规范割集准则、比例割集准则、平均割集准则、最大最小割集准则、多路规范割集准则等[19]。

谱聚类根据确定的划分准则对无向图进行划分,使子图内部的相似度权重尽量大,子图之间的相似度权重尽量小[20]。虽然谱聚类算法在具体操作方面有差异,但其总体可按以下步骤[21]计算:① 构建表示样本的矩阵;② 求出样本矩阵的特征值和特征向量并对其进行排序,选取前N个特征值和特征向量进行特征空间构建;③ 利用K-means或FCM等经典聚类算法对特征向量空间中的特征向量进行聚类。

2 基于匹配度和谱聚类的知识推荐

2.1 计算知识匹配度

现有文献在计算知识相关性部分时单纯计算用户-知识评分相似度,或更多地从用户-属性相似度入手,或计算相似度时考虑时间、信任度、物品流行度等情境因素,其主要对相似度指标进行调整与计算。由于实践中存在知识项间相似度较高但关联度较低,或相似度较低但关联度较高的情况,鉴于此,本文提出融入知识匹配度的计算策略,将相似度和关联度有机融合而成匹配度。计算知识间匹配度的主要步骤如下。

Step 1 计算知识间视图相似度。构建用户-知识的评分矩阵Rm×n,根据Rm×n中的评分,利用余弦相似度计算知识间的评分相似度,从而得到知识之间的视图相似度矩阵Simn×n,如表3所示。

表3 知识相似度矩阵Table 3 Knowledge similarity matrix

Step 2 计算知识间关联度。利用Apriori算法及其相关原理求出知识项之间关联度并形成关联度矩阵asson×n,如表4所示。

表4 知识关联度矩阵Table 4 Knowledge relevance matrix

Step 3 计算知识匹配度,即对知识间关联度和知识间视图相似度进行赋权融合。根据丁少衡等[22]的研究,利用线性融合的方式对二者进行赋权融合,如式(4)所示,其中权重系数采用sigmoid函数进行确定,如式(5)所示,

M(i,j)=α(i,j)×Sim(i,j)+

(1-α(i,j))*asso(i,j),

(4)

(5)

其中:α为权重系数;Iu是某用户u同时对知识项i、j进行评分的次数。

计算匹配度矩阵Mn×n,其中Mn×n为对称矩阵,如表5所示。

表5 知识匹配度矩阵Table 5 Knowledge matching matrix

对于稀疏矩阵来说,如果知识项共同评分过少,且只对知识评分矩阵进行相似度计算,由于用户评分偏好或项目流行度等其他方面的影响,得到的相似度结果很有可能与实际的相似度值有偏差。从式(4)、(5)可以得出,若知识项i和j有较高的共同评分次数,则匹配度中知识项视图相似度的比重更大;若知识项i和j有较低的共同评分次数,则匹配度中知识项属性关联度的比重更大。

2.2 知识项谱聚类

知识推荐系统通常拥有庞大的知识储量。若对知识库中每一个知识项的匹配度进行两两对比、排序,得到匹配度最大的知识项,会大大增加现有系统计算的复杂度和时耗。为了解决上述问题和缩小遍历范围,采取谱聚类对匹配度较高的项目进行聚类,对既有知识进行簇内知识项的匹配性比较。对知识项进行谱聚类的主要步骤如下。

Step 1 将匹配度矩阵Mn×n作为无向图中的权值矩阵,即邻接矩阵W输入,当i=j时,wij=0,构造的矩阵W为

Step 2 根据权值矩阵W和式(6)构造矩阵D,其中下标为(i,i)的元素对应矩阵W中第i行元素的和。采用规范拉普拉斯矩阵L,其构造方法如式(7)所示,其中I为n阶单位矩阵,

(6)

(7)

Step 3 求拉普拉斯矩阵L的前k个最小特征值和特征向量,k为聚类个数,构成矩阵S=[s1,s2,…,sk]。

Step 4 用K-means聚类算法对特征向量进行聚类,聚类簇数为K,聚类簇中的知识项分别为C1,C2,C3,…。如果矩阵S的第i行被聚类算法划进第k类,则知识项的第i项被划进第k类。

2.3 评分预测及推荐

完成上述步骤后,结果为谱聚类的簇和知识项所在的簇序号,以此预测缺失项的评分。缺失项的预测评分也作为对用户推荐知识项的依据;同时,通过对缺失项评分的预测可更直观地对现有推荐系统的推荐结果以及推荐效率进行评估。评分预测及推荐的步骤如下。

Step 1 寻找并锁定每个知识项所在的聚类簇,对簇内的知识项根据知识匹配度降序排列。

Step 2 预测评分。根据簇内知识项的匹配度顺序及其大小,依据式(8)预测缺失的用户对某知识项的评分,以此生成用户评分预测矩阵r_prem×n,

(8)

Step 3 结合预测评分对用户进行推荐。根据式(8),对评分的预测是基于该知识项现有评分,将各个知识项的平均值作为用户的偏好标准。当预测评分高于偏好标准,即认为用户对该知识项有偏好倾向,则将该知识项向用户进行推荐。同理,当预测评分低于偏好标准,即认为用户对该项目不具有偏好倾向,则不向用户推荐该知识项。

3 实验与分析

3.1 实验数据集

选用推荐领域常用的Movielens数据集来检验所提算法的可行性和优越性。实验部分采用Movielens-100k数据集,其包含943位用户对1 682部电影的10万条评分数据。按照80%和20%的比例随机划分训练集和测试集,将电影作为知识项,将电影的类别标签作为类别属性进行实验,则知识项共有18种不同类别的属性。

3.2 评价指标

均方误差用于衡量推荐预测值和真实值之间的误差,其值越小说明误差越小,推荐模型拟合程度越好。计算公式为

(9)

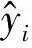
准确率是对“用户是否满意”这个指标进行正确判定的比例,其值越大,说明用户对推荐结果的满意度越高。计算公式为

(10)

其中:TP为测试集中将正类判定为正类的集合;FN为测试集中将正类判定为负类的集合。

3.3 参数选取

实验通过对不同聚类簇数的MSE和准确率指标的对比来确定聚类簇数的取值。取聚类簇数K=2、5、8、10、12、15、20、25、30、40、50进行对比,MSE的结果如图1所示,准确率的结果如图2所示。

图2 不同聚类簇数的准确率对比Figure 2 Comparison of accuracy of different cluster numbers

由图1可知,MSE值的变化情况是下降到一个极小值后再上升,在K=20时,MSE为最小值。在K≤30时,聚类簇中只有一个知识项的聚类簇数目增多,处于这些聚类簇内的知识项在簇内并没有近邻知识项。根据式(8)推断,位于该聚类簇内部的知识项的预测评分用该知识项的平均分代替,而这个结果影响了预测评分的准确性。同时,随着知识项聚类数目的增多,很多匹配度较高的知识项并没有被划分到同一类中,从而出现预测值偏低的情况。而当K≤10时,聚类算法形成的聚类簇过少,造成匹配度不高的知识项也被划入同一簇,从而使同一用户对于被预测知识项匹配度较低的知识项的评分,也在一定程度上对该项的评分预测有影响,增大了评分预测结果的误差。

由图2可知,准确率的值随着聚类簇数波动,但其变化总体呈现下降趋势,在K=20时,准确率为局部极大值。因此,综合考虑,取K=20。

在计算关联度过程中,最小支持度阈值σ对匹配度的计算结果也有影响。根据实验所采用数据集的情况(数据集包含1 682项知识项,18种知识属性)综合考虑,本文的最小支持度阈值σ=1。

3.4 结果分析

将本文算法与基于项目的协同过滤算法(ICF)和基于最近邻法的协同过滤推荐算法(KNN-ICF)[23]进行对比,结果如图3和图4所示。因聚类簇数K=20,所以KNN-ICF算法的最近邻值取每个簇簇内知识项数的平均值,即最近邻数为80。

图3 不同算法的MSE对比Figure 3 Comparison of MSE of different algorithms

图4 不同算法的准确率对比Figure 4 Comparison of accuracy of different algorithms

由图3和图4可知,本文算法的MSE值均低于ICF和KNN-ICF算法,准确率则高于ICF和KNN-ICF算法。其中,相较ICF算法,本文算法的MSE值降低了4.69%,准确率提升了18%;相较KNN-ICF算法,本文算法的MSE值降低了14.9%,准确率提升了18%。

4 结语

传统的基于项目的知识推荐仅比较项目间的相似性,忽视了其存在的关联性,导致知识服务方在知识推荐过程中可能出现忽略知识之间相似度较低而关联度较高的情况,从而束缚了知识推荐效益。鉴于此,本文提出将相似度与关联度融合成知识匹配度,并以此作为知识推荐的基础。在此基础上,利用谱聚类算法压缩遍历空间,以提升计算效率,对比实验结果表明本文算法优于传统算法。但本文算法尚存在以下不足:① 尚未考虑时间维度延展对知识推荐效果的影响。知识效用与热度(生命周期)、用户的偏好等因素均会随着时间的推移而变化,从而对知识推荐效果产生影响。② 尚未解决在知识推荐领域存在的冷启动问题,亦未考虑矩阵稀疏性对推荐效果的影响。这将是下一步研究的方向。