一种求解Max-SAT问题的快速模拟退火算法
吴宇翔, 王晓峰,2, 于 卓, 谢志新, 莫淳惠, 曹泽轩
(1.北方民族大学 计算机科学与工程学院 宁夏 银川 750021; 2.北方民族大学 图像图形智能处理国家民委重点实验室 宁夏 银川 750021)
0 引言
可满足性问题(satisfiability problem,SAT)是如今计算机科学和人工智能研究的核心问题,也是著名的NP完全问题[1]。在理论研究与实际应用方面,有着至关重要的作用。人工智能中的大多数难解问题,诸如规划问题、组合优化问题等都可通过编码技术转为SAT问题,再利用SAT问题求解器求解。随着SAT问题的迅速发展,很多实际问题更多时候需要的是更优解,而不仅仅用“是”或“否”来判断,使得很多学者便开始研究SAT的优化问题,如Max-SAT问题、Min-SAT问题、SMT问题、QBF问题[2-5]等。
最大可满足性问题(maximum satisfiability,Max-SAT)是SAT问题的一种优化版本,指寻找一组布尔变元赋值,使得满足的子句数目最多。Max-SAT问题在统计物理、机器人路径规划[6]、组合拍卖和概论推理等领域有着广泛的应用,同时图论中的最大割问题和最大团问题[7]也可以转换成Max-SAT问题进行求解。目前,求解Max-SAT问题的算法一般分为基于回溯机制的完备性算法和基于局部搜索的非完备算法。完备性算法可以保证找到最优解,主要代表有WmaxSatz[8]、MiniMaxSat[9]等,但在求解大规模问题时,由于复杂度高,难以在合理时间内找到结果,求解效率较低。相对于完备性算法,非完备性算法不保证一定能找到问题的精确解,但可通过问题的特性利用启发式策略,在短时间内找到一个较好解,并在面对大规模问题实例时,该类求解方法有很重要的实际意义。
近些年,随着物联网和大数据技术的迅速发展,数据量越来越大,Max-SAT的问题规模也逐渐增大,求解Max-SAT问题的原有算法已不再适用,设计新的求解算法或对已有的求解算法进行优化是目前研究的热点。已有求解Max-SAT问题的算法主要包括遗传算法、禁忌搜索算法、蚁群算法、正交免疫克隆粒子群算法、人工蜂群算法、模拟退火算法和路径重连算法[10-16]等。其中模拟退火算法是一种经典的基于局部搜索的智能优化算法,作为一种有效的非线性组合优化算法,该算法具有较好的局部搜索能力,并且理论基础十分完善。目前,模拟退火算法已应用于各种组合优化问题,文献[17]将模拟退火算法求解TSP问题。文献[18]使用模拟退火算法求解构造路径规划问题,但是对于Max-SAT问题,传统的模拟退火算法存在搜索的盲目性和随机性、收敛速度慢等问题。
本文提出了一种改进的快速模拟退火算法(quick simulated annealing algorithm, QSA)求解Max-SAT问题。在QSA中,算法的初始解不是随机生成,而是利用变元权值计算[19],生成一组初始解,为了进一步提高算法的局部搜索和收敛能力,采用降温函数进行分段,起到快速降温的效果;同时,在降温过程中引入不同的干扰策略和在Metropolis接受准则中加入记忆功能[20],确保在同一温度下,找到局部最优解。对该算法的性能进行实验分析,数值结果表明:QSA算法无论是在易解区域还是难解区域都能取得较好的性能,与传统的启发式搜索算法相比,有较好的优越性。因此,QSA在求解Max-SAT问题方面起到了积极作用。
1 最大可满足性问题(Max-SAT)
1.1 相关定义
Max-SAT问题是SAT的优化形式,先对Max-SAT的构成要素进行说明。
定义1文字。每一个布尔变元X={x1,x2,…,xn}={0,1}n,变元xi取正时表示正文字;变元xi取反时表示负文字。
定义2子句。C={c1,c2,…,cm},对m个不同的子句形成一个子句集合,每一个子句由一个或多个文字组成,文字与文字之间通过析取运算连接,记c=x1∨x2∨…∨xn,当且仅当子句中至少有一个文字为1时,该子句满足,反之子句不满足。
定义3合取范式(conjunctive normal form,CNF)。由若干个子句合取构成,即F=c1∧c2∧…∧cm,当且仅当CNF公式的每一个子句都满足时,称合取范式CNF可满足。
定义4最大可满足性问题Max-SAT。给定一组命题变元xi∈X,由这些变元形成一组子句,构成CNF公式,使得CNF公式中满足子句的个数最多,也就是使得不满足的子句个数最少。Max-SAT问题的数学模型为
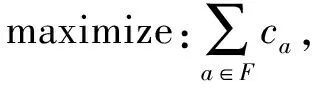
(1)
ca∈{0,1},xi∈{0,1},
(2)
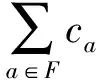
1.2 问题转换
Max-SAT问题中每个子句中的变元取值都具有离散的特性,依据命题逻辑理论的相关结论,可以将Max-SAT问题转成一个求解定义在{0,1}n的多项式函数f(X)的最大值的优化问题。令l={x1,x2,…,xn},其是由n个0或1的整型变元构成的集合,其中l中的xi对应子句c中的变元xi,1-xi对应xi。于是在CNF公式中,F=c1∧c2∧…∧cm,可将符号∧看成一种普通的加法,而子句中c=x1∨x2∨…∨xn,可将符号∨看成一种特殊的乘法,记1⊕0=0⊕1=1⊕1=1,0⊕0=0。例如:CNF公式中,F=(x1∨x2∨x3)∧(x1∨x3∨x4),其中子句分别对应c1=x1⊕x2⊕(1-x3),c2=x1⊕x3⊕(1-x4),函数f(X)=c1+c2=(x1⊕x2⊕(1-x3))+(x1⊕x3⊕(1-x4)),假设一组赋值X={x1=0,x2=1,x3=0,x4=1},可以得到f(X)=1,即最多满足一个子句。因此,求解Max-SAT问题就可以转化成
2 改进的快速模拟退火算法
2.1 传统的模拟退火算法
模拟退火算法(simulated annealing algorithm,SA)是一种全局统计优化算法,其思想来源于模拟对固体进行退火的过程,当固体物质温度很高时,固体内部粒子做杂乱无序的运动;当温度逐渐降低时,固体内部粒子运动逐渐有序,最终,整个物体达到内能最低,便处于稳定状态。利用对温度逐渐降低的过程,使算法在解空间中搜索出一个最优近似解。
模拟退火算法常常用于求解组合优化最小值问题,随机初始一组解,以该解为起点,在同一温度下,不断地对变元赋值进行干扰,从而产生新解,将新旧解进行比较,然后利用Metropolis接受准则判断是否接受新解。假设当前解为xold,干扰后得到新解xnew,若新解的内能Enew小于当前解的内能Eold,即ΔE=Enew-Eold<0,则接受该新解。否则,则以概率exp[-(Enew-Eold)/T]接受新解。重复上述过程,随着迭代次数的增加和Metropolis接受准则对新解的判断,逐渐向该温度下的最优解靠近,当温度达到限制的迭代次数后,依据冷却进度表中的温度衰减函数进行降温,再重复上述过程,最终可以求得问题的整体最优解。标准Metropolis准则表示为

(3)
其中:k代表卡尔兹曼常数;T代表当前状态下的温度。
对于Max-SAT问题,设X={x1,x2,…,xn}是一组布尔赋值,把目标函数定义为不可满足的子句数目,即找到不可满足的最少子句数。如式(4)和式(5):
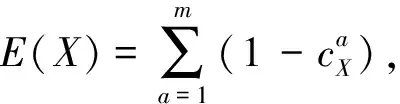
(4)
变元x若满足子句,则子句为1,否则子句为0;

(5)
算法1传统模拟退火算法
输入:初始温度为t0,停止温度为tf,迭代次数为n。
输出:输出最优解。
Step1:初始化温度t0,初始解x={x1,x2,…,xn},并计算目标函数E(x)。
Step2:同一温度下,在解空间产生一个随机的扰动,生成新解y={y1,y2,…,yn},并计算目标函数E(y)。
Step3:若E(y)
Step4:若达到热平衡,即达到迭代次数n,转step5,否则转step2。
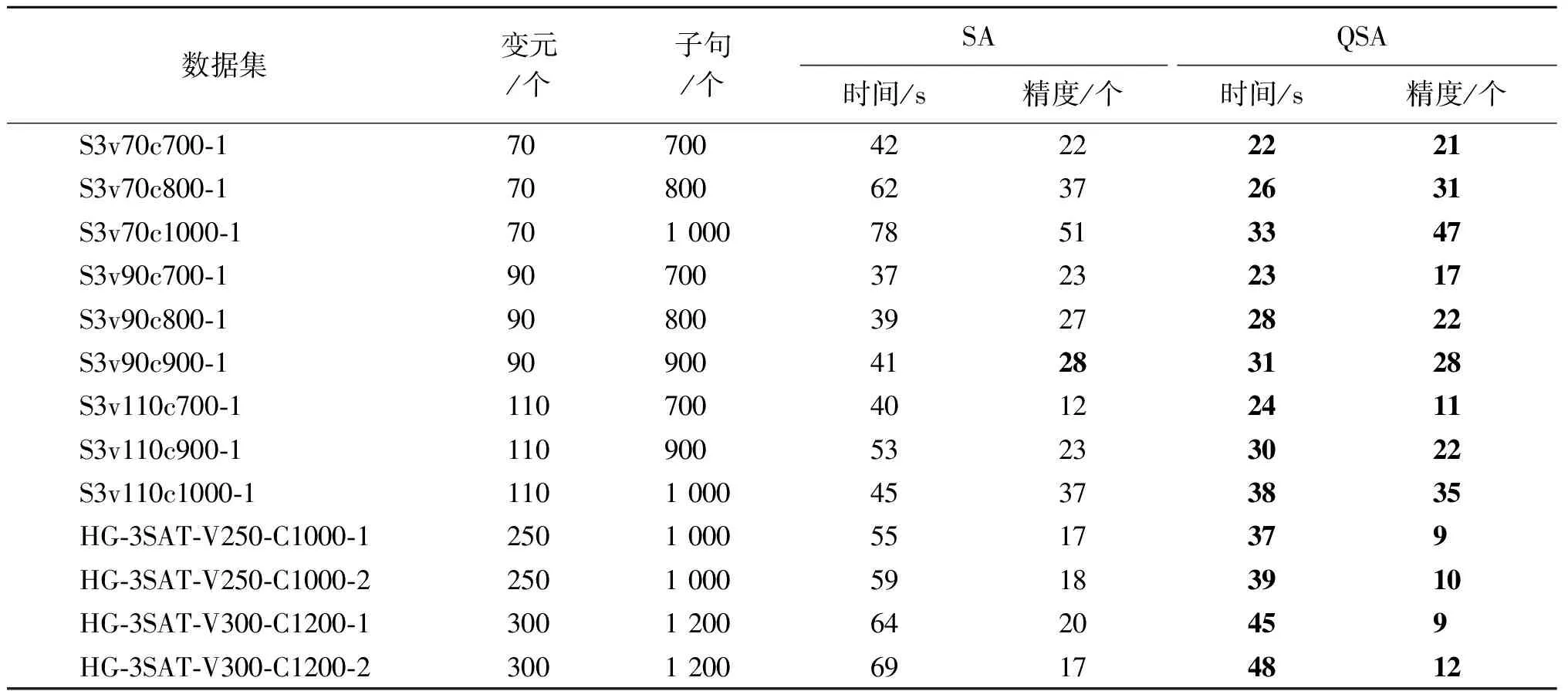
Step5:降低温度tk,若tk 传统模拟退火算法在求解Max-SAT实例时,会出现效率很低、盲目搜索、收敛慢等问题,为弥补传统模拟退火算法的不足,进行以下3个方面的策略改进,优化其性能,可更快速高效地求解出最优的结果。 2.2.1变元权值计算 局部搜索算法中,搜索过程占用了整个算法的大多数时间,普遍的随机搜索算法的初始解都是随机生成的,会出现一定的随机性,当初始解比较好时,可以高效地找到有效解,而初始解不好时,会浪费很长时间从而降低了算法的性能,同时还会重复访问一些解。本文提出的变元权值计算,利用变元在整个子句集中出现的次数来决定对变元的赋值,从而得到一组有效的初始解。对于每一个变元都会记录一个正或负权值,根据该变元正负文字出现的差异,变元的权值代表着变元可能为正或负的程度。如果变元的权值为正,则代表该变元在整个子句集中出现正文字的次数较多,反之,若权值为负,则代表出现负文字的次数较多。权值计算公式为 (6) 其中:Number(PosLit)代表变元在整个子句集中出现正文字的次数;Number(NegLit)代表变元在整个子句集中出现负文字的次数;Number(Clausevar)代表变元在整个子句集中出现的次数。 2.2.2降温函数 在传统的模拟退火算法中,初始温度和终止温度的设置是影响整个模拟退火算法全局搜索性能中重要的因素之一,初始温度足够高,则搜索到全局最优解的可能性就越大,但是会花费大量的计算时间,反之,则可以节约时间,但搜索结果会受到影响。传统模拟退火算法在降温过程中采用T=T0α的指数函数进行降温,其中T0是当前温度,α是退火过程中温度衰减率,通常取值为0.7<α<1.0。有研究表明,使用传统的模拟退火算法求解Max-SAT问题,当温度较高时,满足的子句个数较少,而温度较低时,满足的子句个数越多,其求解效率较高。基于此问题,本文提出一种快速分段降温函数如式(7)所示,在温度较高时,采取高温退火,快速降温,提高求解时间,而温度较低时,采用低温退火,慢速降温,在低温情况下,进行充分搜索,寻找其局部最优解,使得算法的整体收敛速度加快,从而有效减少求解时间。 (7) 其中:T0是当前温度;α是退火过程中温度衰减率;k是迭代次数;1/N通常取值为0.5或1。 上述两种降温函数,均是指数形式。T0>10代表的是高温退火阶段,T0≤10代表的是低温退火阶段。高温退火阶段能够快速降温,再利用低温退火阶段进行局部搜索。在求解Max-SAT问题时,采用分段降温的方法能够快速高效地找到最优解。 2.2.3干扰策略 传统的模拟退火算法具有随机性和盲目性,而且容易陷入局部最优,无法快速有效地找到最优解等问题。基于此本文作出改进,在算法刚开始时温度很高,目标函数值很大,则对变元赋值进行干扰后接受新赋值的概率较大,所以需要在大范围的空间里对变量赋值进行随机扰动,以防陷入局部最优。随着温度的降低,则有针对性对变元赋值进行有策略地扰动。具体地讲,在算法刚开始时,温度很高,以1-3/T作为选择不同扰动方案的概率,若小于此概率,便进行随机扰动,对解进行随机生成;若大于此概率,便进行有策略扰动,随机挑选一个变元,对该变元进行翻转,从而产生新解。同时,本文在Metropolis接受准则中加入记忆功能,在同一温度下,进行多次干扰后,会记录一个局部最优值,以防丢失。当整个降温结束时,在记录表中直接找到全局最优解即可。 改进的快速模拟退火算法的流程如算法2,具体步骤如下。 算法2改进的快速模拟退火算法(QSA) 输入:初始温度t0、停止温度tf、阈值温度te、迭代次数L、衰减函数α、当前迭代次数k。 输出: 输出最优解。 Step1:初始化温度t0,初始解x={x1,x2,…,xn},并计算目标函数E(x)。 Step2:随机取一个0~1的实数rand0。 Step3:IF(rand0<1-3/T) {对解进行重新随机生成赋值,从而得到新解y={y1,y2,…,yn},并计算目标函数E(y)}。 ELSE{随机选择一个变元进行翻转,从而得到新解y={y1,y2,…,yn},并计算目标函数E(y)}。 step4:计算ΔE=E(y)-E(x)。 IF(ΔE<0) {无条件接受新解y={y1,y2,…,yn}和目标函数E(y)}。 ELSE{随机生成一个0~1的随机数rand1}。 IF(rand1>exp[-(E(y)-E(x))/T]){接受新解y={y1,y2,…,yn}}和目标函数E(y)。 ELSE{接受旧解x={x1,x2,…,xn}和目标函数E(x)}。 step5:将该温度下最优值记录到记录表中。 step6:若达到热平衡,判断k>L是否满足,若是,转step7,否则转step2。 Step7:判断是否达到终止条件tk Step8:判断温度是否达到阈值温度,若tk>te,采取高温退火,若tk 为了准确评估本文提出的改进快速模拟退火算法QSA在解决Max-SAT问题的有效性。分别对算法QSA、SA、WalkSAT、GA、CCEHC和HS-Greedy进行测试。其中WalkSAT、SA和GA为经典的启发式算法,CCEHC和HS-Greedy 为2016年Max-SAT Evalution 国际竞赛的求解器。本次实验采用Python语言在AMD R7-4800U,1.80 GHz的64位PC端进行。采用的是随机生成的3-SAT实例和2016年Max-SAT Evalution国际竞赛中随机类的数据集,分析其求解精度和求解时间。 算法QSA设置的参数初始温度t0为100 ℃,终止温度tf为0.01 ℃,阈值温度te为10 ℃,马氏链长度L为300,衰减函数α为0.95。其中阈值温度te范围设置为5 ℃ 对于随机生成3-SAT实例,生成模型如下。随机均匀地从所有可能的子句(子句共有23×(n3)T)中选出m(m=αn)个子句。选出的子句以合取的方式连接,其中:n代表变元个数;m代表子句个数,子句长度为3;约束密度为α=m/n。约束密度α对CNF公式的可满足性以及可满足性判定的难易程度会产生重要的影响,几乎所有算法的求解效率均与约束密度α密切相关。有学者研究表明,随着约束密度α的增大,当3.52<α<4.48时,会发生相变。在相变范围以外的可满足性实例均为易解实例,高概率是可满足的;在相变点附近的实例属于难解实例,高概率是不可满足的。 针对随机生成3-SAT实例,表1是将本文算法QSA和遗传算法GA进行实验对比,采取约束密度α分别为4.5、5、10、15、20,变元个数为50,子句个数分别为225、250、500、750、1 000进行数值实验分析,比较两种算法的求解时间(s)和求解精度(最少不满足子句个数),其中加黑字体为算法对比当前最优解。实验表明,随着约束密度的增加,不满足子句个数也逐渐增加,同时两种算法的求解时间也在增加,但QSA在求解精度和求解时间方面均远远优于GA,由此说明QSA算法求解随机生成的3-SAT实例中优于传统启发式算法。 表1 随机生成实例中QSA和GA在求解精度和 时间上对比Table 1 Comparison between QSA and GA in solving precision and time in randomly generated examples 表2给出QSA、WalkSAT、CCEHC和HS-Greedy四种算法的实验比较,采用2016年Max-SAT Evalution国际竞赛中随机类的3种易解数据集的17个实例(变元个数分别为70、90和110,子句个数分别为700、800、900、1 000、1 200),在最少不满足子句个数上进行实验对比,其中加黑字体为算法对比当前最优解。从表2中可以看出,CCEHC效果最好,17个实例中有15个实例都取得了最好结果,而本文提出的QSA算法有14个实例效果最好,略差于CCEHC,但相较于WalkSAT和HS-Greedy两种算法,本文算法QSA在求解精度上远远优于这两种算法,其原因在于WalkSAT和HS-Greedy算法的搜索具有随机性和盲目性,而本文提出的QSA算法使用了新的初始解生成方式,通过降温函数和扰动策略降低了搜索过程中的随机性和盲目性,所以在求解性能上会有优势。因此,QSA算法在求解易解实例问题上具有一定的有效性。 表3是QSA、WalkSAT、CCEHC和HS-Greedy四种算法在难解实例中的算法对比,采用的是2016 年 Max-SAT Evalution 国际竞赛中随机类的HG-3SAT-V250-C1000和HG-3SAT-V300-C1200两个难解数据集(3-SAT实例,当变元个数为250时子句个数为1 000,当变元个数为300时,子句个数为1 200)。每一类数据集中有5组数据,其中加黑字体为算法对比当前最优解,比较四种算法最少不满足子句个数。由表3可以得出CCEHC不满足子句个数最少,10组数据中其均是排名第一,而本文提出的QSA算法略差一些,但仍然优于WalkSAT和HS-Greedy算法。通过表2~3数据可以发现,文本提出的算法QSA在求解易解实例时效果很好,但在求解难解实例时效果略差一些,其原因在于难解实例结构特性较复杂,导致在进行局部搜索时,搜索程度不够深入,搜索策略可能会陷入局部最优,从而导致求解性能略差于CCEHC,存在的这些问题也是算法今 表2 QSA、WalkSAT、CCEHC和HS-Greedy在易解实例中算法对比Table 2 Algorithm comparison of QSA, walksat, ccehc and HS greedy in easy to understand examples 单位:个 表3 QSA、WalkSAT、CCEHC和HS-Greedy在难解实例中算法对比Table 3 Algorithm comparison of QSA, walksat, ccehc and HS greedy in hard to solve examples 单位:个 后需要改进的地方。 表4是将本文提出的QSA算法和传统模拟退火算法SA的实验对比,采用的是2016 年 Max-SAT Evalution 竞赛中随机类数据集在求解精度和求解时间上进行比较,其中精度是指最少不满足的子句个数,时间是算法运行时间,加黑字体为算法对比当前最优解。由表4可以看出,在求解精度和求解时间上,QSA算法的性能都优于SA算法。QSA算法加入变元权值计算和干扰策略后,在加快求解速度的同时求解精度也得到了提高。SA算法在整个退火过程中,随机扰动很多,具有收敛慢的特点,而QSA算法采用分段降温的方式,在高温区域可以快速降温,在低温区域进行局部搜索大大提高了求解效率,从而避免了随机扰动和搜索的随机性。由此可得,改进后的模拟退火算法在求解Max-3-SAT问题时取得了很好的效果,且具有一定的稳定性,在求解精度上,QSA也优于SA,验证了本文算法的有效性。 表4 QSA和SA在求解精度和时间上对比Table 4 Comparison between QSA and SA in solution accuracy and time 本文提出一种改进的快速模拟退火算法,主要是对算法的初始解进行变元权值计算,并在降温过程中,使用高低温分段两种降温方式,同时根据Max-SAT问题的特性,采取不同的扰动策略,在Metropolis接受准则中加入记忆功能,从而提高算法在局部搜索过程中的精准度,找到当前满足最多子句的个数,加快整个算法的求解效率,避免算法陷入局部最优,实现精准高效求解,并利用公开数据集进行实验,进一步验证算法的有效性。通过实验对比发现,本文算法不论在易解实例还是难解实例,都表现出优异的求解效率,其结果为以后的理论研究提供了参考价值。虽然本文提出的算法在求解时间和精度方面远远优于传统模拟退火算法,但当问题规模进一步增大时,整个算法的计算复杂度增加导致花费时间增加,后续研究可以从利用模拟退火算法的可并行性和与其他智能优化算法相结合的策略来入手,从而提高算法性能。2.2 改进的快速模拟退火算法
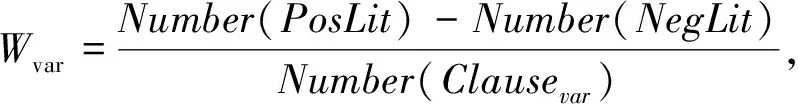
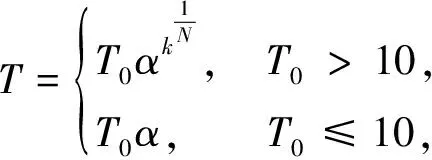
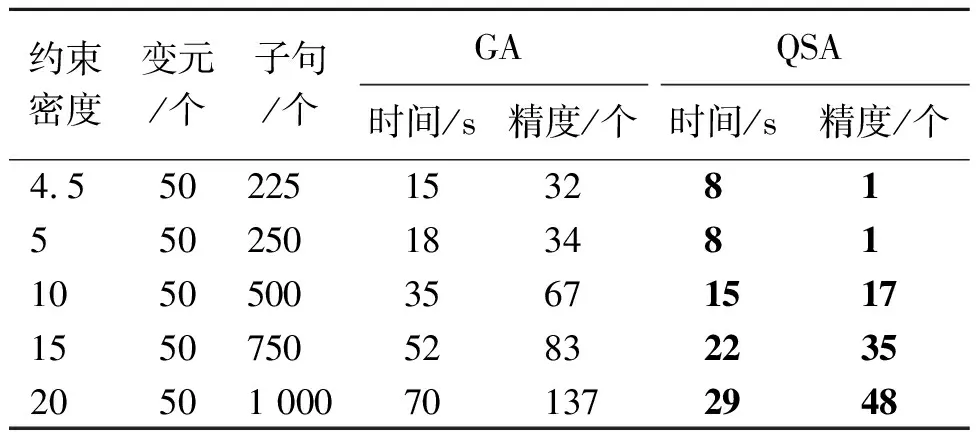
3 实验仿真及分析


4 结束语

