基于级联效应的水库调度决策多维综合评估

张世锴,王义民,郭爱军,畅建霞

(西安理工大学 省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048)

0 引言

水库优化调度可以充分利用水库的调蓄作用,最大限度地提高水库兴利效益,其旨在通过建立水库优化调度模型,采用优化算法对模型进行求解,获得最优水库调度决策[1]。迄今为止,学者们对于水库调度优化模型以及求解算法[2-3]做了大量的研究,对模型的求解时间和求解精度方面都做出了很大突破[4-5]。需要注意的是,受气象预报[6]、径流预报[7]和需水预测[8]的不确定性以及应急突发用水事件等多种因素的影响,实际的调度过程往往会与优化调度决策出现偏差[9],进而对后续调度过程带来不利影响,即水库某月水位扰动对后续优化调度过程产生级联性影响。科学评估水库调度决策的级联效应,掌握水库调度运行中对水位扰动最为敏感的月份,对提升水库调度决策的稳健性以及最大程度保证水库调度兴利效益的实现具有重要的指导作用。

级联效应[10]是指:网络中的一些节点由于受扰动而导致功能缺失甚或丧失,此类问题节点不能再承担“流”,导致网络中的“流”在节点上重分布,可能会造成新的节点功能缺失甚或丧失。这一现象将导致问题节点在整个网络中蔓延,对网络造成极大破坏。关于级联效应的研究横跨多个领域,例如在电力系统[11]、因特网系统[12]、交通系统[13]和物流系统[14]等领域对于其系统内部的级联效应都做出了大量研究。关于级联效应,MOTTER等[15]以最大连通子图规模为评估指标,研究了网络在随机和针对扰动下发生级联效应的情况,结果表明:删除承担“流”的能力最强的节点时,易引发级联效应。闫妍等[16]在构建弹性供应链网络时,提出要考虑级联效应对节点重要度的影响,并提出了评估节点重要度的方法。在对级联效应的研究中,普遍认为网络中的节点只存在正常和功能丧失2种状态。但实际上节点并不是直接由正常状态变为功能完全丧失状态,而是有一个节点承担“流”的能力逐渐变弱的过程,即节点在正常和功能丧失状态之间还存在一种过渡状态,该状态下的节点仍然能承担负载,只是承担能力比正常状态弱。考虑到这一情况,吴俊等[17]通过定义过载函数来表示这3种状态,在发生级联效应时不会删掉出现问题的节点,只是在“流”重新分配时会绕开这些节点。

目前,水库调度研究领域对级联效应涉及较少,为了对水库调度中的级联效应有更充分的认识,文中从调度决策扰动对水库兴利调度服务对象的影响持续时间、整体兴利效益损失程度与单一时段服务对象生产功能丧失程度3个角度来考虑级联效应对水库调度的综合影响,提出了基于级联效应的水库调度决策重要度评估方法以及级联效应等级划分方法,能够有效识别出影响水库防洪、兴利调度的关键月份,同时也能对不同程度水位扰动下产生的级联效应的强度等级进行衡量。以上工作对于提升水库调度决策的稳健性,促进水库兴利效益目标的可实现性,降低服务对象兴利效益的风险性等方面具有很大的实用价值,同时扩展了级联效应的研究范围,丰富了水库优化调度的研究内容。

1 水库调度决策研究

水库优化调度可以看作是一个利用水库的调蓄作用和控制能力,将水库来水按照最匹配调度目标的方式分配到各调度时段上,从而达到兴利除害的目的[18],其中,水库(群)优化调度的核心为水库水位的科学控制。以供水为目标的长系列水库调度为例来开展水库调度决策[19]。首先要在来水预报的基础上考虑水库蓄水量的可供水量,同时需要水库供水对象的需水预测数据;其次,核定用水计划,即分析水库可供水量能否满足供水对象的用水需求,如果可供水量不能满足供水对象的用水需求,需要根据水量分配原则做一定的折减;最后,建立供水调度模型,采用优化算法求解出水库优化调度决策方案。

可以看出来水预报和需水预测都是供水调度过程中的关键一环,由于受来水预报和需水预测的不确定性以及调度过程中的突发用水事件等的影响,上述方法得到的调度决策方案可能并不适用于指导整个水库调度过程。故有学者将不确定性的供需水过程作为供水调度模型的输入来推求水库优化调度方案[20-21],但是其调度结果比以确定性供需水过程作为输入下的优化调度结果差距较大,该方法还有待完善。文中考虑径流预报、需水预测不确定性等因素对调度过程稳健性的影响,研究如何避免影响较大的级联效应发生,有助于获得最大的兴利效应。

2 水库调度中的级联效应研究

2.1 水库调度级联效应描述

在水库调度过程中,受径流预报不确定性等因素的影响导致某一阶段水库蓄水不足,此时,水库将根据自身水位以及所承担任务进行自适应优化,寻找新的优化调度决策,即新的水库水位运行最优状态。由于水库调度过程中的调度决策对于这种变化的适应能力的有限性,当水位受到扰动时,可能会使得众多调度决策过程受到不利影响,以供水为目标的水库为例,将导致后续一段时间内的供水量降低以及破坏深度加重,最终使得调度结果远不及预期,这就是存在于水库调度中的级联效应,如图1所示。随着级联效应的发展,水库恢复正常调度的能力会不断下降,因此需要在调度决策影响很小时阻止级联效应的发生,避免经济、社会效益损失。

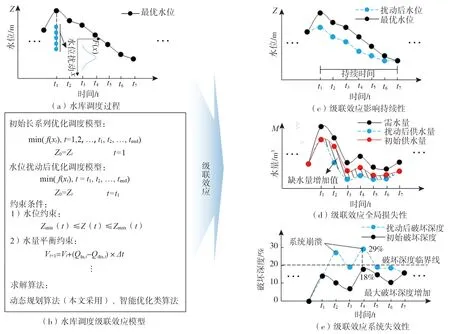
图1 水库调度级联效应示意图Fig. 1 Schematic diagram of cascading effects of reservoir operation

在各种因素的影响下,水库调度过程中水库水位会受到不同风险频率的扰动,且不同风险频率的水位扰动造成的影响程度不同。为了衡量各时段调度决策的重要程度,需要结合不同水位扰动程度出现的风险频率来考虑,若用pk表示水位扰动出现的风险频率,则级联效应下的调度决策的综合重要度计算公式为:

(1)

式中:f综合,i为第i个时段的综合重要度;fk,i为风险频率pk的水位扰动下的调度决策重要度,该值通过2.3.1节的公式计算得到。

水库调度过程中各时段水库水位的扰动以及同一时段水库水位不同幅度的扰动,都可能会对整个调度过程产生不同程度的影响,这就需要我们找到受水位扰动而对调度结果产生较大影响的调度决策,从而帮助决策者对其进行重点调控,使水位尽可能达到优化调度决策水位。

2.2 水库调度级联效应多元评估体系构建

如果要评估系统中某一部分的重要性,只需将该部分破坏掉或直接从系统中删掉,使其无法正常发挥作用,然后确定该部分的功能丧失会对系统造成破坏,破坏程度越高,也就说明该部分对于整个系统越重要,这是一种基于系统科学范畴的方法[22]。系统科学分析方法的突出特点[23]是:通过某一部分被破坏后,系统受到的影响来发掘复杂系统中的关键部分。文中为了分析水库调度过程中的级联效应,从水库水位扰动对服务对象的影响持续时间、整体兴利效益损失程度与单一时段服务对象生产功能丧失程度3个方面出发,提出了面向影响持续性、全局损失性以及系统失效性的水库调度决策级联效应评估指标,构建出了基于级联效应的水库调度多元评估体系。

2.2.1 级联效应影响持续性

当水库水位受到扰动后,为了使长系列水库调度结果保持最优,以扰动发生时为初始时刻,重新建立水库优化调度模型,求解出后续最优调度决策。此时,会发现受级联效应影响,水位扰动后的一段时间内水库供水情况会发生变化,即后续一段时间内的调度决策会受到级联效应的影响,导致供水量下降,进而影响到调度目标,将受影响的这段时间称之为级联效应的持续时间。文中通过影响持续性指标来描述水库调度级联效应的影响传播范围,指标值越大,表明级联效应影响的时间越长。其计算公式如式(2)、式(3)所示:

(2)

(3)

式中:PER为级联效应的持续性;N为水库调度的周期;ri为第i个调度决策时段的影响值;q0,i为初始状态第i个时段的缺水量;q1,i为受级联效应影响后第i个时段的缺水量。

2.2.2 级联效应全局损失性

级联效应造成的全局损失性通过水库水位扰动后,在级联效应的持续时间内,对供水系统供水量造成的破坏程度来衡量。节点的全局损失性指标值越大,供水量下降程度越大,表明整体兴利效益的损失越大,水库调度级联效应下全局损失性的计算公式[24]如式(4):

GBLi=Ei/E0-1

(4)

式中: GBLi为全局损失性;E0是水库优化调度时的缺水量;Ei是指第i个时段水位扰动引发级联效应后水库调度缺水量。

2.2.3 级联效应系统失效性

破坏深度是指水库调度中缺水量与需水量的比值,文中认为若某一调度时段对应的破坏深度大于20%,则该时段处于功能完全丧失状态,表明此时的供水系统遭到了严重的破坏。受级联效应的影响,可能会导致一些原来未处于功能丧失状态的时段转化为功能丧失状态。采用系统失效性来衡量受级联效应影响供水系统功能的损失程度,系统失效性越大,表示水库调度供水系统受级联效应影响,遭到破坏的程度越严重。对于一些水库调度系统而言,会出现受级联效应影响的持续时间很短,但每次受到破坏的程度很大的情况,这对大多数用水户(尤其是城市生活、工业用水)而言,是不可接受的。破坏度与系统失效性的计算公式如式(5)、式(6)所示:

Di=Qi,que/Qi,xu

(5)

(6)

式中:Di,Qi,que,Qi,xu分别为第i个时段对应的破坏度,缺水量,需水量;VUL为系统的脆弱性;d1,i为受级联效应影响的时间内第i个时段的状态,若当前时段处于功能丧失状态,则u1,i= 1,若当前时段未处于功能丧失状态,则u1,i= 0;u0,i为初始状态第i个时段的状态,其大小的判定与u1,i一致;D1,max为级联效应影响持续时间内的最大破坏度;D0,max为上述时间内初始状态下的最大破坏度。

2.3 水库调度级联效应综合评估

识别出水库调度中的重要调度决策具有很高的应用价值,有助于水库调度风险防控,获得更大的综合效益。文中为了定量评价水库调度过程中各阶段发生级联效应的重要程度,根据描述级联效应的3项指标值,基于TOPSIS方法计算出各阶段的综合级联效应。不同强度的水位扰动产生的级联效应强度不同,因此,对各调度决策扰动产生的级联效应进行等级划分可以为如何应对级联效应提供决策依据,有助于减轻级联效应带来的综合不利影响,文中根据描述级联效应的3项指标值,采用K-means算法对各阶段的级联效应进行分类。

2.3.1 基于TOPSIS的综合级联效应计算

逼近理想解排序法[25-26](TOPSIS)根据评价对象与理想化解的接近程度对评价对象进行排序。在TOPSIS方法中,有2个理想化解,分别是正理想解和负理想解,其中正理想解也被称为最优目标,负理想解也被称为最劣目标。在排序过程中,评价对象与理想化解的接近程度通常采用欧氏距离计算,该方法排序结果最优的对象与正理想解最接近,而排序结果最劣的对象与负理想解最接近。

文中基于TOPSIS的水库调度系统时段综合重要度计算步骤如下:

1)构造决策矩阵:

(7)

式中:m为评估时段的数量;n为每个时段的指标数量; 第i个评估节点的第j个指标的值为Cj(vi)。

2)规划化决策矩阵:

(8)

3)构造权重规范化矩阵:将规划化决策矩阵的第j列乘以其权重得到加权规划化决策矩阵C(cij)m×n。

4) 确定正理想解C1和负理想解C0:

(9)

(10)

式中:

(11)

(12)

5)计算每个待评估节点到正理想解和负理想解的欧氏距离,待评估节点到正理想解的距离为S1,到负理想解的距离为S0:

(13)

(14)

6)计算理想解的贴近度fi,fi的计算公式为:

(15)

式中:fi∈[0,1],贴近度越大,节点的重要度越高。

2.3.2 基于K-means算法的综合级联效应等级评估

K-means算法的基本原理是[27-28]:以使得目标函数最小为目的,将n个对象的实测数据分成组,每个组为每一分类,得到的聚类结果中,每个分类至少包括一个数据对象,同时每个数据对象仅能属于一个分类。

该算法以分类数K为参数,将n个对象分成K类,以同一类中的数据对象的平均值为中心进行分类。K-means算法聚类步骤为:

第1步:确定分类数目K;

第2步:随机选取K初始的中心,然后根据各数据到各中心(平均值)的距离进行分类,在此基础上重新计算各分类的平均值。以上过程反复迭代,最终使得目标函数值最小。通常在K-means聚类算法中采用的目标函数为:

(16)

式中:P为数据对象;ci为组C的中心;E为所有数据对象的平方误差和; 目标函数最小使得各个分组里的数据尽量紧凑。

第3步:重新计算各个组中心,即重新计算各组中个数据对象的均值,并以各个均值点作为每个分类的中心点。

第4步:若各组的中心不再变化,则返回划分结果,否则转至第2步。

3 实例研究

3.1 区域概况与调度模型选择

3.1.1 区域概况

东庄水库位于黄河二级支流泾河下游峡谷末端陕西省咸阳市礼全县东庄乡。东庄水库承担有供水、发电及防洪等任务,其总库容 32.76亿m3,调节库容5.78亿m3,为不完全年调节水库;电站装机容量为110 MW,水库正常蓄水位789 m,汛限水位780 m,死水位756 m,汛期为7—9月。

数据资料收集方面,东庄水库1960—2009年入库径流采用张家山水文站对应年份还原后的径流资料。需水资料中,工业、生活及生态需水量来源于《陕西省泾河东庄水利枢纽工程水资源论证报告书》;农业灌溉需水量通过Penman-Monteith公式结合作物系数法乘以相应作物灌溉面积。其中,各月多年平均需水总量见图2,需水量最多的月份是在7—8月,其次为4—6月,而10月份的需水量最少。

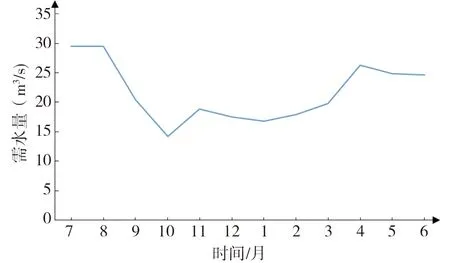
图2 各月多年平均需水总量Fig. 2 Average annual total water demand per month

3.1.2 调度模型选择

文中选择总缺水量最小作为水库优化调度模型的目标函数。

目标函数——缺水量最小,如式(17)所示:

(17)

式中:M为总缺水量,单位为m3;Qi,xu为第t个时段的需水量,单位为m3。qt为t时段水库泄流量,单位为m3/s。

约束条件:

1)水位约束:

Zmin(t)≤Z(t)≤Zmax(t)

(18)

式中:Z(t)为t时段库容;Zmin(t)、Zmax(t)分别为t时段的水位下限、上限,单位为m。

除此之外，可变剪接也对小干扰多肽起着调控作用。转录因子在此过程中扮演着核心角色。转录因子是基因表达调控研究领域的“明星”————一个转录因子可以影响一系列下游的基因在何时何地表达，甚至表达量的多少。有一类转录因子，由于其存在一段多聚化功能区域，需通过形成二聚体才能发挥作用。

2)水量平衡约束:

Vt=Vt-1+(Qt+Qt-1)Δt/2-(qt+qt-1)Δt/2

(19)

式中:Vt为t时段水库库容,单位为m3;Qt为t时段水库入流量,单位为m3/s;Δt为时间间隔,单位为s。

3)生态流量约束:

qt≥qs

(20)

式中,qs指生态基流,单位为m3/s。

4)泄流能力约束:

(21)

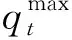
5)初始和边界条件:

Z1=ZN=ZC

(22)

式中:Z1为初始水位;ZN为结束水位;ZC设定为死水位,单位为m。

6)非负约束:以上所有变量都是非负的。

文中采用动态规划(DP)算法[29-30]来对水库优化调度模型进行求解,使用DP算法求解水库优化调度决策时,首先把一个调度周期分为若干个时间段,从而将水库调度决策变为一个多阶段决策的问题,然后通过正时序或逆时序进行逐步求解,最后获得整个调度周期的最优水库调度决策。

3.2 东庄水库优化调度节点重要度评估

3.2.1 东庄水库优化调度研究

东庄水库各月库容分布情况见图3,从图中可以看出,7—8月份的水库水位变化幅度较大,9—11月份的水库水位较高,尤其是10月份的水库水位有大概率位于正常蓄水位,后续水库水位逐渐下降。通过构建东庄水库供水优化调度模型,并对模型进行求解,获得东庄水库1960—2009年月尺度的优化调度策略。将水库的优化调度结果与模拟调度结果进行比较(其中模拟调度为以需定供的调度过程),可以看出,优化调度策略对来水的分配更加合理,能够充分利用水库的调蓄功能,50 a来可以向用水户多供水63 415万m3。需要注意的是,在实际调度过程中,由于受径流预报不确定性等多种因素的影响,导致不能对水位做到精准调控,最终影响到调度结果。这就需要我们识别出水库调度过程中的关键节点,对关键节点水位进行重点调控,从而获得最大的兴利效益。

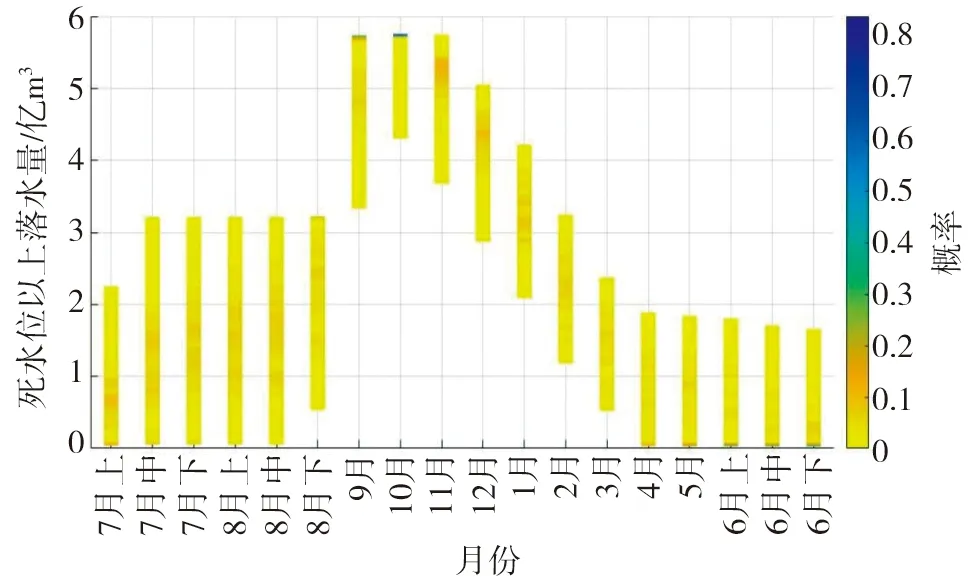
图3 水库各月库容概率分布图Fig. 3 Probability distribution map of reservoir capacity in each month

3.2.2 水库调度决策级联效应的多维评估

在实际水库调度过程中不同程度的水位扰动产生的级联效应的影响程度不同,且水库水位受到不同程度扰动的风险频率也不相同。为了分析东庄水库调度过程中的级联效应,用水库蓄水量的破坏来表示水库水位的扰动,文中设计出5种不同的破坏方案,见表1。计算各方案下每月的全局损失性、影响持续性及系统失效性指标值,取各月多年平均指标值作为每种方案最终的指标值,指标计算结果见图4。

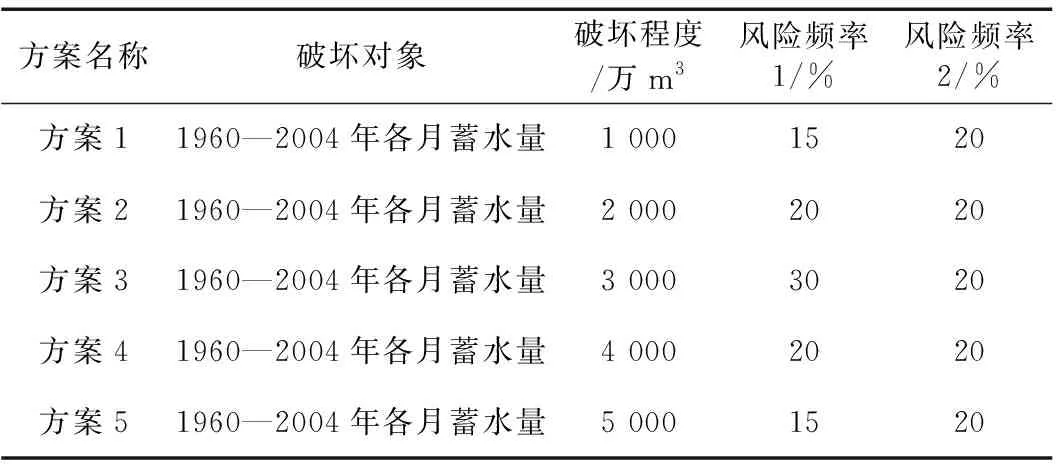
表1 破坏方案Table 1 Sabotage plan

从图4中可以看出,水文年初(7月)及水文年末(5—6月)的各项指标值都较小,其原因为7月开始进入汛期,来水逐渐增多,在这之前对水库蓄水量进行破坏后,通常能在汛期快速恢复过来。9—10月影响持续性标值最大,表明这2个月份调度决策下引发的级联效应持续时间通常较长,其原因为从10月开始进入枯水期,该时期对用水户的供水需要依靠水库在汛期的蓄水量,如果水库蓄水量不足,将会对用水户在整个枯水期的用水造成一定的不利影响。若某一年来水较少,6月水库水位已降到死水位,那么该年内发生的级联效应最长持续到6月,因为6月的水位保持不变,在同样的来水条件下,6月以后的水位会与最初的优化调度求解出的决策水位保持一致。若年末水位没有位于死水位,那么级联效应通常会持续到下一水文年汛期,此时,大量的来水能够修复级联效应带来的持续影响。因此,某一年内发生级联效应,其结束时间多是水文年末或下一水文年汛期初期。

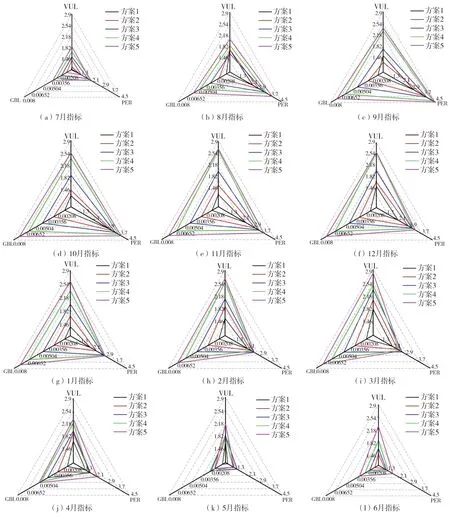
图4 不同方案下各月指标统计Fig. 4 Monthly indicator statistics under different schemes

9—次年3月的全局损失性指标值较大,表明这几个月份发生级联效应时将导致水库供水总量极大下降,其主要原因是当这些月份的蓄水量受到破坏后,后续时间内的来水量多小于需水量,水库水位得不到补充,被破坏掉的这部分水本是需要供给到用水户的,所以会导致用水户端缺水量增大。3月系统失效性指标较大,表明当3月份的水库蓄水量遭到严重破坏时,将造成用水户的极端缺水情况发生,这是需要避免的,其原因为水库水位在枯水期不断下降,到3月份时,水库供水能力已严重不足,这时对水库蓄水量进行破坏,通常会使得后续枯水月供水系统的破坏深度严重加重。

通过对3类指标的分析可以发现,影响持续性指标随着水库蓄水量的破坏加重,其敏感性变弱,这是由于水库特性和来水特征导致的,水库水位扰动下的级联效应的持续时间有一个最大阈值,即水位扰动发生到后续初始优化调度过程中决策水位第1次为死水位的这段时间(见图5)。相较于影响持续性指标与系统失效性指标,东庄水库调度决策对全局损失性指标更加敏感,其中在枯水期时尤为显著。

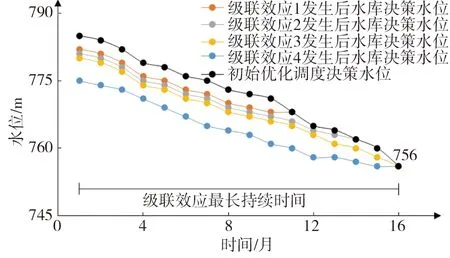
图5 级联效应最长持续时间示意图Fig. 5 Schematic diagram of the longest duration of the cascade effect

3.2.3 水库调度决策级联效应的综合评估

受级联效应影响,为了识别出不同月份调度决策的重要程度,文中根据式(1)以及上述基于加权欧氏距离的TOPSIS法计算得到不同方案下的调度决策综合重要度,并通过得到的5种方案下的各月产生级联效应3种评价指标的加权值,采用K-means算法将其强度划分为3类,得到不同等级的级联效应,按照级联效应由弱到强分为1～3级,结果见表2。从调度决策重要度计算结果中可以看出,重要度最高的调度决策月份是10月,因此,在水库调度过程中保持该月的水库水位正常运行十分关键,如果其水位未能调蓄到优化调度决策水位,可能会对用水户在整个枯水期的用水带来较大的不利影响。5—7月的重要度最低,因为7月份开始进入汛期,在这之前水库蓄水量被破坏后,大量的来水能够用于补充库容,水位很快便能恢复过来,造成的综合影响较小。

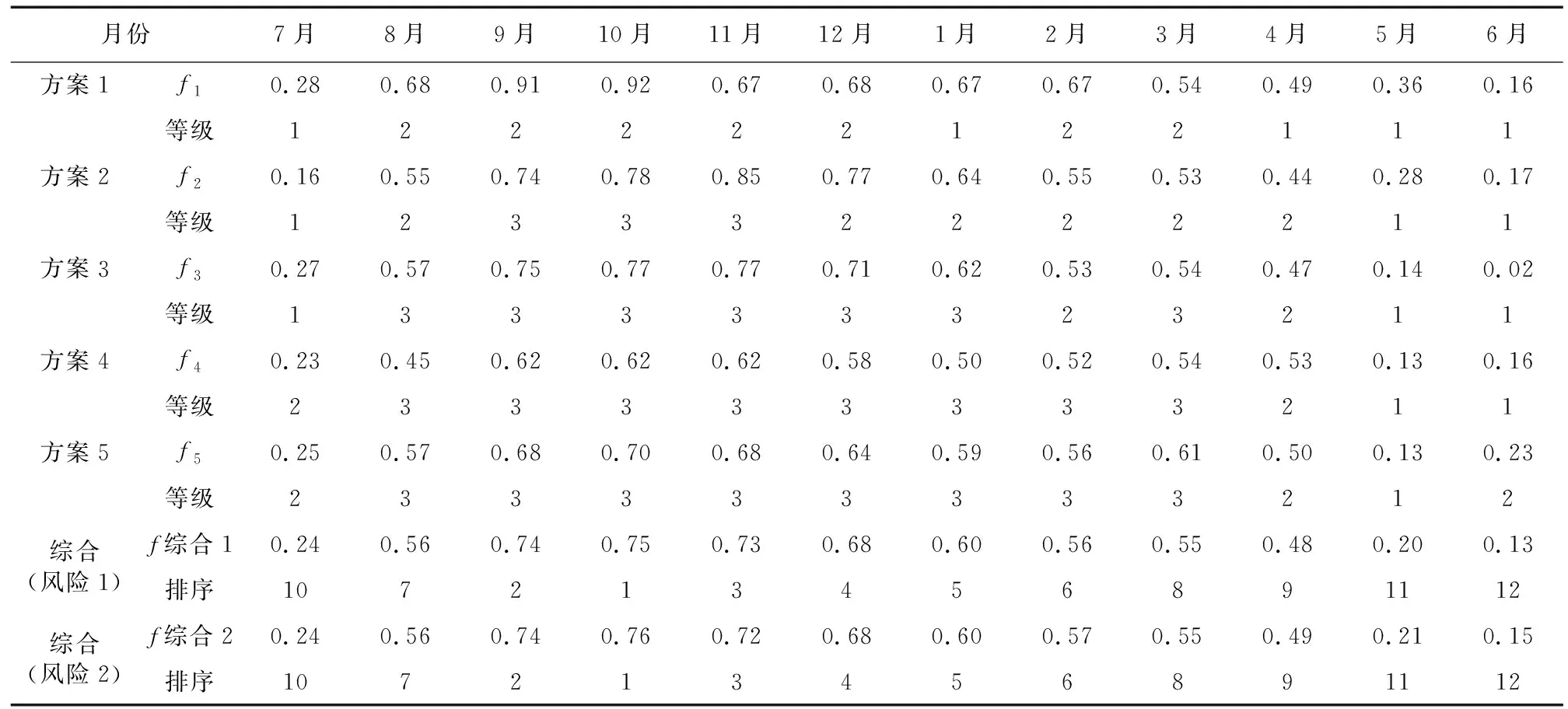
表2 调度决策重要度计算结果及级联效应分类表Table 2 Calculation results of the importance of scheduling decisions and the classification table of cascading effects

水库调度过程中不同月份发生级联效应对水库兴利效益的实现造成的影响程度的不同,文中通过影响持续性、全局损失性和系统失效性3个指标对水库调度过程中不同月份发生级联效应造成的影响程度进行衡量,结果表明在水库调度过程中当在9—11这3个月发生级联效应时,会对水库兴利效益的实现造成较大的不利影响,其次是1—4、8、12月份发生级联效应时,往往也会造成一定的不利影响,而5—7月份发生级联效应时,其对水库兴利效益的实现所造成影响有限。

不同程度水位扰动下产生的综合级联效应强度体现出较大的差异性,虽然通过重要度计算方法得出考虑综合级联效应的3月调度决策重要度小于9月,但是受3 000万m3蓄水量破坏的3月水库水位扰动下产生的级联效应强度大于受1 000万m3蓄水量破坏的9月产生的级联效应。因此,有必要对不同程度水位扰动下产生的综合级联效应强度进行分级,这可以为级联效应发生后的应对方案提供决策依据,从而将级联效应造成的损失降到最低。

4 结论

水库调度过程受到气象预报、径流预报和需水预测的不确定性以及突发用水事件的影响而易发生级联效应,研究如何避免级联效应发生以及对级联效应进行分级应对,有助于提升水库调度决策的稳健性,促进水库兴利效益目标的可实现性,降低服务对象兴利效益的风险性。文中从水库水位扰动对服务对象的影响持续时间、整体兴利效益损失程度与单一时段服务对象生产功能丧失程度3个角度出发,构建出基于级联效应的水库调度决策重要度评估指标体系,以此为基础,采用TOPSIS方法量化各时段水库调度决策级联效应,应用K-means算法划分水库调度决策重要程度等级。以东庄水库为研究实例对象,建立了通过水位扰动模拟出水库调度级联效应的供水优化调度模型,结合该模型计算出了不同风险频率水位扰动下产生的级联效应,并对其进行等级划分。主要结论如下:

1)影响持续性指标随着水库蓄水量的破坏加重,其敏感性变弱,相较于影响持续性指标与系统失效性指标,东庄水库调度决策对全局损失性指标更加敏感,其中在枯水期时尤为显著。

2)通过基于级联效应的东庄水库调度决策综合评估方法,确定出东庄水库调度过程中重要度最高的月份是10月,即同一程度的水位扰动下,10月水库调度决策产生的级联效应最为显著。决策者对该月水位进行重点调控,有助于避免破坏程度较大的综合级联效应发生,从而提升东庄水库兴利效应目标的实现。

3)通过对级联效应的强度进行等级划分,为当级联效应发生后,如何应对级联效应提供决策依据,有助于减轻级联效应带来的综合不利影响;未来,将本文所提级联效应研究方法应用到多年调节水库、复杂供水网络体系等是该研究的重点关注方向。