一类格竞争系统的双稳周期行波解*
李 俭
(西安电子科技大学 数学与统计学院, 西安 710071)
0 引 言
本文主要研究下面的格竞争系统双稳周期行波解的存在性:
(1)
其中uj(t),vj(t)表示u,v两个物种在t时刻、位置j处的种群密度,d1,d2分别是物种u,v的扩散系数,ri(t)是种群内的内禀增长率,bi(t)是两种群之间的竞争系数,ai(t)表示种群自身的死亡率.ri(t),ai(t),bi(t)(i=1,2)∈C2()且为T-周期函数,即∀t>0,ri(t+T)=ri(t),ai(t+T)=ai(t),bi(t+T)=bi(t), 此外,di>0,ai(t)>0,bi(t)>0,∀t∈[0,T].
系统(1)为下面时间周期Lotka-Volterra竞争扩散系统的空间离散形式:
目前,有关Lotka-Volterra竞争系统行波解的研究已经越来越广泛.Bao和Wang在文献[1]中研究了时间周期Lotka-Volterra竞争系统双稳周期行波解的存在性和稳定性.Fang和Zhao在文献[2]中研究了部分退化反应扩散系统的的单调行波解.Li在文献[3]中研究了一类部分退化合作系统行波解的存在性.Zhao和Ruan在文献[4]中研究了Lotka-Volterra竞争扩散系统的时间周期行波解的存在性、唯一性和渐近稳定性.Hao、Li和Wang在文献[5]中研究了Lotka-Volterra 竞争系统空间周期的整体解和传播动力学.Bao、Li和Wang在文献[6]中研究了Lotka-Volterra竞争扩散系统的时间周期行波解的渐进行为.在实际生活中,种群的活动空间通常是不连续的,因此考虑空间离散模型对生物种群动力学的研究具有重要的实际意义,同时,离散化后形成的格微分方程具有更丰富的动力学行为.Guo和Wu在文献[7-8]中分别讨论了自治情形下Lotka-Volterra格竞争系统的单稳和双稳行波解的存在性和单调性.Wang和Ou在文献[9]中讨论了Lotka-Volterra格竞争系统的传播方向和波速符号.Shen在文献[10]中讨论了二维格反应扩散方程双稳周期行波解的存在性与唯一性.考虑到物种的生存环境(例如温度)和物种的死亡率、出生率会随季节发生周期性改变,故在模型中加入周期.综上,研究系统(1)的周期行波解对于预测物种的竞争情况有重大意义.为方便讨论,给出假设条件:
(A1)(双稳性假设)

系统(1)所对应的空间齐次系统为
(2)
在假设条件(A1)下,系统(2)存在4个非负的周期解(0,0),(p(t),0),(0,q(t)),(u★(t),v★(t)),此时,(p(t),0),(0,q(t))在+的内部是稳定的,(u★(t),v★(t))是不稳定的.其中p(t),q(t)表示如下:
为方便讨论,先做一个变换:
(3)
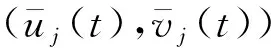
(4)
由变换(3),系统(1)的周期解(0,0),(0,q(t)),(p(t),0),(u★(t),v★(t))为对应系统(4)的周期解(0,1),(0,0),(1,1),(u*(t),v*(t)).定义:0=(0,0),1=(1,1).因此研究系统(1)连接两个稳定半平凡平衡点的双稳周期行波解就转化成了研究系统(4)连接两个稳定边界平衡点的双稳周期行波解.令
下面给出周期行波解的定义.

进一步,若U(ξ,t)关于ξ∈还是单调非减的,则称U(ξ,t)是一个周期波前解.
本文通过构造合作系统(4)的上下解,并且建立比较原理,进而证明了当初始函数满足一定条件时,解在无穷远处收敛,并采用黏性消去法证明了系统(4)连接0和1的双稳周期行波解的存在性.具体的思路是∀D>0,构造一个系统(4)的波相系统的辅助系统:
(5)
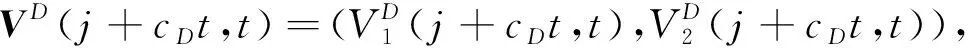
本文的剩余部分内容如下:第1节给出了一些假设条件、重要函数及引理;第2节给出了系统(4)的一对上下解和比较原理;第3节利用黏性消去法证明了系统(4)双稳周期行波解的存在性;最后一节给出了本文的结论.
1 预 备 知 识
令
u=(u,v)T,f(u,t)=(f1(u,v,t),f2(u,v,t))T,Δ2[u]=u(ξ+1,t)+u(ξ-1,t)-2u(ξ,t).
假设:
(H1)f:2×→2, (u,t)→f(u,t)∈C2,
(H2)f(u,t+T)=f(u,t),

1≤i≤k},∀x∈k.对于η=(η1,…,ηk),η′=(η′1,…,η′k),∀1≤i≤k,若ηi≥η′i,则称η≥η′.若ηi>η′i,则称η≫η′.若η≥η′且η≠η′,则称η>η′.令C是k中的所有有界双边点序列组成的集合, 对于u=(uj)j∈,v=(vj)j∈∈C,类似上面的定义,有∀j∈,若uj≥vj,则称u≥v.若uj>vj,则称u≫v.若u≥v且u≠v,则称u>v.任意m中的向量可认为是m中的常数点序列, 且令
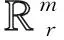

引理1 令v(x)是Kr+2ρ={x∈:|x|≤r+2ρ}(r>0,ρ>0)上的可积函数,且对|Δx|≤ρ,s∈[0,r+ρ],有其中ws(·)是一个连续非减函数且ws(0)=0,则对h≤ρ,有Jr(vh,Δx)≤wr+h(|Δx|)且
证明该引理的证明可参考文献[12].
2 上下解与比较原理
本节给出了系统(4)的上下解,建立了无界域上的比较原理,根据文献[13-16],首先给出上下解的定义.
定义2 若一对连续函数(u(ξ,t),v(ξ,t))在×[0,+∞)上除了有限个点(ξi,ti),i=1,2,…,n外都是可微的,且满足对∀t≥0,ξ∈成立
(6)
则称(u(ξ,t),v(ξ,t))是系统(4)的下解.通过改变不等式的方向可得系统上解的定义.
令
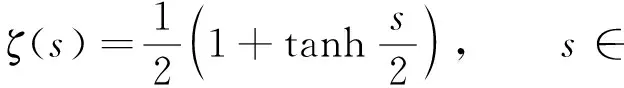
(7)
则有0<ζ(s)<1,ζ′(s)=ζ(s)(1-ζ(s)),ζ″(s)=ζ(s)(1-ζ(s))(1-2ζ(s)).因此ζ′(s)>0,|ζ″(s)|≤1,基于以上理论基础,给出系统(4)的上下解.
引理2 ∀α±∈2且α-≪α+,当C充分大时,则函数
是系统(4)的一对上下解,其中u(t;α±)是u′(t)=f(u,t),u(0,α)=α∈2的解.
证明在该引理的证明中,仅证明v+(ξ,t)是一个上解, 下解的证明可类似得到.首先,令
则
(ui(t;α+)-ui(t;α-))(Cζ′(ξ+Ct)-diΔ2ζ(ξ+Ct))+
fi(u(t;α+),t)ζ(ξ+Ct)+fi(u(t;α-),t)(1-ζ(ξ+Ct))-
fi(u(t;α+)ζ(ξ+Ct)+u(t;α-)(1-ζ(ξ+Ct)),t).
对任意的ξ∈,t>0,由Taylor展开公式得
ζfi(u(t;α+),t)+(1-ζ)fi(u(t;α-),t)-fi(u(t;α+)ζ+u(t;α-)(1-ζ),t)=
ζ[fi(u(t;α+),t)-fi(u(t;α+)ζ+u(t;α-)(1-ζ),t)]+
(1-ζ)[fi(u(t;α-),t)-fi(u(t;α+)ζ+u(t;α-)(1-ζ),t)]-
fi(u(t;α+)ζ(ξ+Ct)+u(t;α-)(1-ζ),t)=
(uj(t;α+)-uj(t;α-))(uk(t;α+)-uk(t;α-)),

令

其中,z(ξ,t)∈(v(t;α-),v(t;α+)),t≥0.则
Li[v+](ξ,t)≥
故v+(ξ,t)是系统(4)的上解,引理得证.
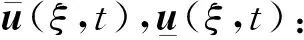
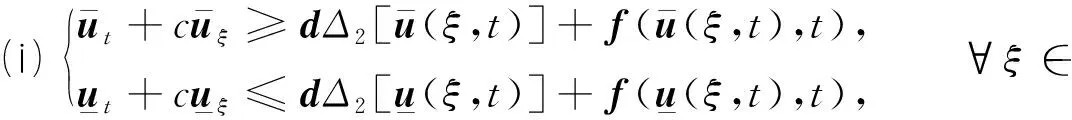
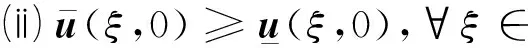


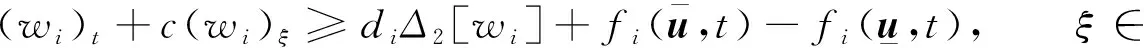
(8)
选择充分大的K>0,满足(7/4)K-|c|-(3/2)Lf-max{d1,d2}>0,其中


令ζ0(ξ)是一个光滑函数,满足minξ∈ζ0(ξ)=1, 当ξ∈S,ζ0(ξ)=1, supξ∈ζ0(ξ)=ζ0(±∞)=3,


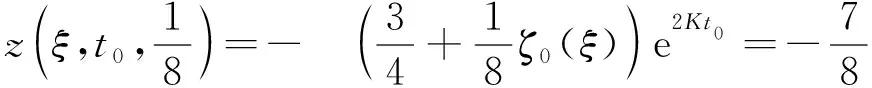
定义α*=inf{α∈(1/8,1/4]|wi(ξ,t)≥z(ξ,t,α),∀ξ∈,t∈[0,t0]}.根据定义,有wi(ξ,t)≥z(ξ,t,α*),由于wi(ξ,0)≥0>z(ξ,0,α*);z(±∞,t,α*)≤-(9/8)e2Kt
[-L,L]×[0,t0]处达到最小值0,则H(ξ1,t1)=0,Ht(ξ1,t1)≤0,Hξ(ξ1,t1)=0,由式(8)且wk(ξ,t)≥0可得
0≥Ht(ξ1,t1)+cHξ(ξ1,t1)-di[H(ξ1+1,t1)+H(ξ1-1,t1)-2H(ξ1,t1)]≥



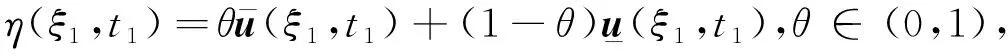
3 双稳周期行波解的存在性
本节利用黏性消去法证明双稳周期行波解的存在性,假设条件(A1)对系统(4)成立,在之后出现的定理和引理的叙述中,不再赘述.基于第2节的理论,考虑下面的辅助系统:
(9)
根据文献[11]和文献[17]中的定理5.1和注5.1有:

基于以上结果,下面研究{φD(ξ,t):D>0}在Lloc(2,2)中的列紧性.令VD(ξ,t)=φD(ξ,t), 则VD(ξ,t)满足方程:
ut+cDuξ=Auξξ+dΔ2[u]+f(u,t),
(10)
其中A=(D1,D2)T.
注1 由引理3及双稳性假设,若∀ξ∈,0≤u0(ξ)≤1, 则有0≤u(ξ,t;u0)≤1;由引理4,若∀ξ∈,0≤u0(ξ)≤1且u0(∞)=1,u0(-∞)=0,则u(+∞,t;u0)=1,u(-∞,t;u0)=0.
引理5 {VD(ξ,t):D>0}在Lloc(2,2)是列紧的.


(11)
(12)
对给定的r>0,0 其中Cr是一个依赖于r的常数.根据文献[10]的引理2.1,∀h∈(0,min{1,r/2}],有 由引理4,对D1>0,D2>0,系统(9)有唯一的周期行波解uD(ξ,t)=φD(ξ+cDt,t).由引理5,令Dk→0,c0∈,φ0(·,·)∈Lloc(2,2),满足 φDk(ξ,t)→φ0(ξ,t), a.e. (ξ,t)∈×. 因此存在一个可测集E0⊆满足m(E0)=0,∀t∈E0,有 φDk(ξ,t)→φ0(ξ,t), a.e. (ξ,t)∈. (13) 由φD(ξ,t)关于ξ的单调性,假设0∈E0,∀t∈E0,存在{Dk′}⊂{Dk}满足 φDk′(ξ,t)→φ0(ξ,t), a.e. (ξ,t)∈. 由于φ0(ξ,t)关于ξ是单调的,则0≤φ0(ξ,t)≤1.∀(ξ,t)∈2,令φ0(ξ+c0t,t),断言 则有 对给定的0 由Lebesgue控制收敛定理,对任何具有紧支集的s(·)∈C∞(),有 根据Fubini定理得 基于上述理论,下面给出存在性结果. 定理1 令φ0(ξ,t)由式(13)所定义,则u±(ξ,t)=φ±(ξ+c0t,t)是系统(4)连接0和1的双稳周期行波解.其中φ±(ξ,t)=φ0(ξ±0,t). 考虑 (14) (15) φ0(ξ+c0t+0,t)=φ+(ξ+c0t,t). 则φ±(ξ,t+T)=φ±(ξ,t).下证φ0(∞,t)=1,φ0(-∞,t)=0. 由引理2可知,v+(ξ,t)是系统(4)的上解,由比较原理,有 v+(ξ,t)≥φ0(ξ+ct+0,t), a.e. (ξ,t)∈. 根据双稳假设条件,limn→∞v+(-∞,nT)=0,由于φ0(ξ±0,t)关于t是周期的,所以有φ0(-∞,0)=0.类似可证φ0(∞,0)=1,再根据注1,∀t≥0,φ0(-∞,t)=0,φ0(∞,t)=1,定理证毕. 本文致力于研究格竞争系统的双稳周期行波解.首先,将非单调的竞争系统转化为合作系统,其次,建立了无界域上的比较原理,给出合作系统的一对上下解,最后利用黏性消去法和比较原理的方法证明格竞争系统连接两个稳定周期平衡点行波解的存在性.本文仅研究了格竞争系统双稳周期行波解的存在性,对于行波解的唯一性、稳定性、单调性以及双稳行波的波速符号等问题尚未有任何结果,这将是笔者下一步需要解决的问题.




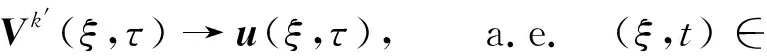
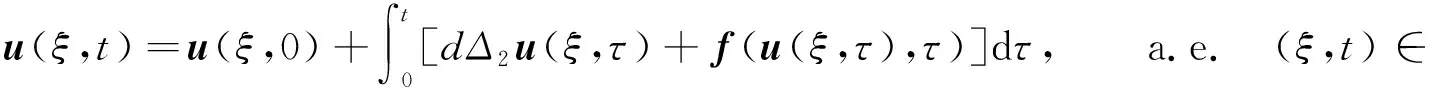
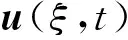
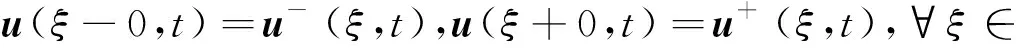
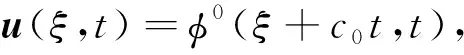
4 结 论

