具有时滞的离散Lotka-Volterra合作系统波前解的非线性稳定性*
闫 瑞, 刘桂荣, 李晓翠
(1. 山西财经大学 应用数学学院, 太原 030006;2. 山西大学 数学科学学院, 太原 030006;3. 北京化工大学 数理学院, 北京 100029)
0 引 言
由专著[1]可知在实际应用中,许多物理学、化学、生物学、传染病学等问题都可以归结为反应扩散方程.所以,研究反应扩散方程的相关内容对生产实践和科学理论具有重要的意义.近年来,关于具有时滞的反应扩散系统的研究是一个重要的课题.因此,本文主要研究如下具有时滞的离散Lotka-Volterra合作系统:
(1)
其中x∈,t∈+,D[w(x,t)]=w(x+1,t)+w(x-1,t)-2w(x,t),w=u,v,所有系数都是正的且时滞τ>0.这里u(x,t)和v(x,t)分别代表x位置和t时刻的人口密度.其初值条件为
(2)
事实上,系统(1)可以认为是如下系统的空间离散化形式:
(3)
显然,系统(1)有4个可能的平衡点

易知,当a1a2-b1b2>0时,ki>0(i=1,2),在系统(3)对应的无扩散系统中,平衡点(0,0)是不稳定的,而平衡点(k1,k2)是稳定的.
在离散方程和系统的研究中,行波解的相关研究也是热点问题之一.对于系统(1) 的连接(0,0)与(k1,k2)的行波解指的是具有如下形式:

且满足

关于不同类型的扩散系统的行波解存在性研究已有了大量的结论,可参考文献[2-8].在关于行波解的研究中,除存在性外,行波解稳定性也是一个比较有趣和困难的问题.关于这方面的研究可参考文献[9-15].对于带有时滞的反应扩散方程,Schaaf首先通过谱分析方法研究了该类方程的行波解的线性稳定性[16].Mei等[17]则利用加权L2能量估计的方法证明了具有时滞的Nicholson方程波前解的非线性稳定性.接着,Mei等在文献[18-20]中应用加权能量法和比较原理,研究了一般的带有时滞的单稳反应扩散方程行波解的全局稳定性.之后,Yu等[21]和Zhang等[22]将加权能量法证明波前解稳定性的方法推广到不同的非局部扩散系统.此外,对于离散扩散方程的行波解的稳定性的研究可以参考文献[23-26].对于离散扩散系统,最近,Chen等[27]及Su等[28]分别运用加权能量结合比较原则证明了一个三种群离散扩散竞争系统的单稳波前解的非线性稳定性.而在文献[29]中,Hsu等运用不同的比较定理,研究了一些离散反应扩散系统行波解的稳定性,这些结论可以广泛应用到诸如多种群Lotka-Volterra合作模型、流行病模型、三种群Lotka-Volterra竞争模型等.但是,目前关于系统(1)的波前解稳定性并没有任何的结论,因此,受文献[17-20]的启发,本文将通过加权能量的方法研究该系统波前解的全局稳定性.
本文的主要内容安排如下: 第1节给出了一些预备知识和符号,并给出了波前解稳定性的主要结果;第2节给出了稳定性的证明;最后给出了本文的结论.
1 预备知识和主要结果
在本节中,我们将引入一些记号以方便叙述并给出主要结论.首先,在本文中,C>0代表一个一般的常数,Ci>0代表具体的常数,I是一个区间,通常I=.其次,L2(I)表示I上的平方可积函数构成的空间,若函数f(x)且其导数dif/dxi(i=1,2,…,k)都属于L2(I),则这些函数构成Sobolev空间Hk(I)(k≥0).进一步,表示加权的L2空间(ω(x)>0),其范数为

令T为一个正常数,B是一个Banach空间.C([0,T];B)表示由[0,T]上的B-值连续函数构成的空间.L2([0,T];B)表示由[0,T]上的B-值L2-函数构成的空间.[0,∞)上的空间可以类似地给出.
接下来,对于λ>0,c>0,定义
Δi(c,λ)=di(eλ+e-λ-2)-cλ+ri,i=1,2.
引理1[30]存在唯一常数c*>0使得
1) 对于任意c>c*,Δ1(c,λ)=0有两个实根0<λ1(c)<λ2(c),且当λ∈(λ1(c),λ2(c)) 时,Δ1(c,λ)<0,当λ∈+[λ1(c),λ2(c)] 时,Δ1(c,λ)>0;
2) 对于任意c>c*,Δ2(c,λ)=0有两个实根0<λ3(c)<λ4(c),且当λ∈(λ3(c),λ4(c))时,Δ2(c,λ)<0,当λ∈+[λ3(c),λ4(c)]时,Δ2(c,λ)>0;
3) 对于任意0≤c
另外,当a1a2-b1b2>0,d1≤d2,r1≤r2时, 对于c>c*, 系统(1)存在连接(0,0)和(k1,k2)的波前解.对于0 在文献[30]的基础之上,本文将进一步研究系统(1)波前解的稳定性.首先给出如下假设: (A1)a1a2-b1b2>0,d1≤d2,r1≤r2, 2r1-d1>0, 2r2-d2>0; (A2) 4a1r1k1>2r1(1+2b1k2)+b1r1k1+b2r2k2+d1, 4a2r2k2>2r2(1+2b2k1)+b1r1k1+b2r2k2+d2. 注1 令a1=2,a2=2.5,b1=1,b2=1,r1=1.5,r2=2,d1=0.1,d2=0.2,通过计算可知假设(A2)是成立的. 为了给出加权能量函数及适当的估计,在此我们定义如下两个关于β的函数: f1(β)=4a1r1k1-2r1(1+2b1k2)-b1r1k1-b2r2k2-d1(eβ+e-β-1), f2(β)=4a2r2k2-2r2(1+2b2k1)-b1r1k1-b2r2k2-d2(eβ+e-β-1). 由假设(A2),易得 f1(0)=4a1r1k1-2r1(1+2b1k2)-b1r1k1-b2r2k2-d1>0, f2(0)=4a2r2k2-2r2(1+2b2k1)-b1r1k1-b2r2k2-d2>0. 再由fi(β)(i=1,2)的连续性,知存在β0>0,使得f1(β0)>0和f2(β0)>0.之后再定义另外两个关于ξ的函数: g1(ξ)=-2r1(1+2b1k2)-b1r1k1-b2r2k2+4a1r1φ(ξ)-d1(eβ0+e-β0-1), g2(ξ)=-2r2(1+2b2k1)-b1r1k1-b2r2k2+4a2r2ψ(ξ)-d2(eβ0+e-β0-1), 其中(φ(ξ),ψ(ξ))是系统(1)的波前解.易得 于是存在足够大的ξ0>0,使得 gi(ξ0)>0,i=1,2. (4) 由上文,我们进一步定义如下的关于β0和ξ0的加权函数: 最后,我们给出本文的主要结论,即系统(1)的波前解的指数稳定性. 定理1 假设(A1)和(A2)成立.令 其中 c1=2r1(1+2b1k2)+b1r1k1+b2r2k2+d1(eβ0+e-β0-1), c2=2r2(1+2b2k1)+b1r1k1+b2r2k2+d2(eβ0+e-β0-1). 0≤u0(x,s)≤k1, 0≤v0(x,s)≤k2, (x,s)∈×[-τ,0], 0≤u(x,t)≤k1, 0≤v(x,t)≤k2, (x,t)∈×+, 其中常数μ>0. 本节将通过加权能量的方法证明本文的主要结论.首先,类似文献[22,27]中的证明,我们可以给出系统(1)的存在性定理和比较原理. 引理2 假设a1a2-b1b2>0, 2r1-d1>0, 2r2-d2>0成立,若初始条件满足 (0,0)≤(u0(x,s),v0(x,s))≤(k1,k2), (x,s)∈×[-τ,0], 那么Cauchy问题(1)、(2)的解存在唯一且满足 (0,0)≤(u(x,t),v(x,t))≤(k1,k2), (x,t)∈×+. 那么 若(u0(x,s),v0(x,s))满足 (0,0)≤(u0(x,s),v0(x,s))≤(k1,k2), (x,s)∈×[-τ,0], 令 (5) 那么 (6) (7) 接下来将分三步来证明主要的结果. 首先,证明u+(x,t)收敛到φ(x+ct).令 其中ξ=x+ct.由式(5)和(6),有 (0,0)≤(U(ξ,t),V(ξ,t))≤(k1,k2), (0,0)≤(U0(ξ,s),V0(ξ,s))≤(k1,k2). 通过计算易得U(ξ,t),V(ξ,t)满足 (8) 式(8)的方程两端分别乘以e2μtω(ξ)U(ξ,t)和e2μtω(ξ)V(ξ,t),其中μ>0待定,可得 -a1r1e2μtωU3+b1r1φe2μtωUV(ξ-cτ,t-τ), (9) -a2r2e2μtωV3+b2r2ψe2μtωVU(ξ-cτ,t-τ). (10) 因此,对式(9)和式(10)分别关于ξ和t在×[0,t]上积分可得 (11) (12) 由Cauchy-Schwarz不等式可得 (13) 其中W=U,V.类似地,对于式(11)和式(12)右端的第二项,有 (14) (15) 将式(13)—(15)代入到式(11)和(12)中,由于对于ξ∈有ω(ξ+cτ)/ω(ξ)≤1,因此 (16) (17) 结合式(16)与式(17),可得 (18) 其中 类似地,当ξ0-1≤ξ≤ξ0时,此时ω(ξ+cτ)/ω(ξ)≤1.然后可得 当ξ0<ξ≤ξ0+1时,此时ω(ξ+cτ)/ω(ξ)=1.然后可得 当ξ>ξ0+1时,此时ω(ξ+cτ)/ω(ξ)=1.然后可得 □ 引理4 设μ1>0是如下方程 (19) 证明由于(0,0)≤(φ(ξ),ψ(ξ))≤(k1,k2)及ω(ξ+cτ)/ω(ξ)≤1(ξ∈),因此,当0<μ<μ1时,可得 □ 然后,将式(19)代入式(18),我们可得如下估计. (20) 之后,我们给出Uξ和Vξ在加权空间中的L2估计.类似地,对式(8)方程两端关于ξ求导并对所得方程的两边分别乘以e2μtω(ξ)Uξ(ξ,t)和e2μtω(ξ)Vξ(ξ,t),可得 r1e2μtωUUξ[2a1φ′-b1ψ′(ξ-cτ)-b1Vξ(ξ-cτ,t-τ)]= r2e2μtωVVξ[2a2ψ′-b2φ′(ξ-cτ)-b2Uξ(ξ-cτ,t-τ)]= 重复上述证明过程可得引理6. 由引理5和6,可得到如下估计. 由于ω(ξ)≥1,运用Sobolev嵌入定理H1()C(),我们得到如下衰减结论. 其次,重复上述证明过程可得引理9. 最后,运用挤压定理并结合引理8与9,可证明定理1成立. 本文运用L2-加权能量方法、比较原理和挤压技术得到了具有时滞的离散Lotka-Volterra合作系统波前解的全局指数稳定性,并解决了离散扩散算子及时滞共同作用下建立能量估计的问题.此稳定性结果可以有助于理解解(u,v)渐近地表现为以正速度c传播的行波解,并且随着时间t的推移,这两个物种趋于合作水平.


2 稳定性的证明
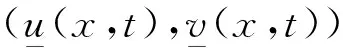



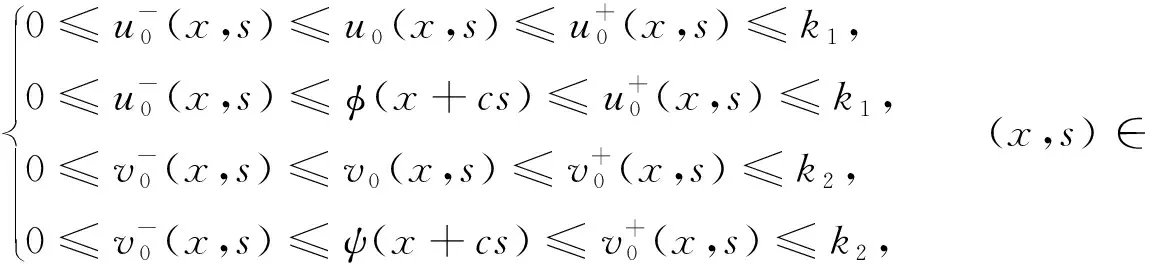

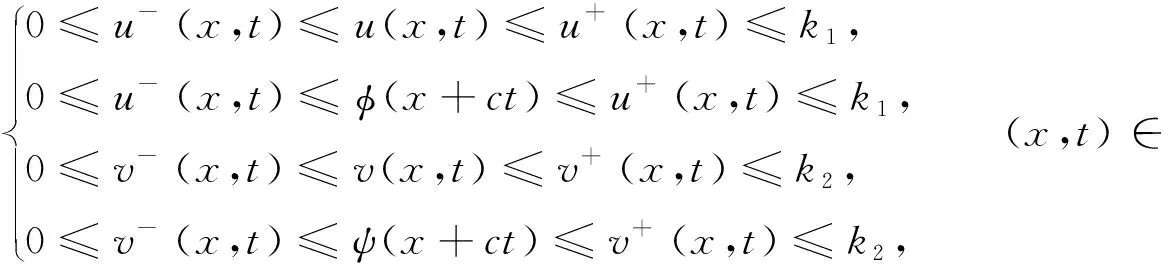
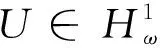










3 结 论

